角加速度信号自适应小波的去噪方法

刘 彤 ， 李 晶 ， 王美玲， 孙荣凯

(1.北京理工大学自动化学院 北京，100081) (2.北京理工大学复杂系统智能控制与决策国家重点实验室 北京，100081)(3.北京自动化控制设备研究所 北京，100074)

角加速度信号自适应小波的去噪方法

刘 彤1,2， 李 晶1,2， 王美玲1,2， 孙荣凯3

(1.北京理工大学自动化学院 北京，100081) (2.北京理工大学复杂系统智能控制与决策国家重点实验室 北京，100081)(3.北京自动化控制设备研究所 北京，100074)

针对多扰动、大负载环境下角加速度计输出信号中含有脉冲噪声和高斯白噪声的情况，提出一种改进的离散小波阈值法与中值滤波算法相结合的角加速度计信号自适应去噪算法。首先，使用中值滤波对原始信号进行去除脉冲噪声的预处理；其次，使用分解层数的自适应确定方法与改进的阈值选取准则，通过离散小波阈值去噪法去除高斯白噪声。仿真结果表明，该算法能够有效地提高信噪比，降低最小均方误差。实验结果表明，该算法既能去除分子型液环式角加速度计信号中噪声，又能很好地保留真实信号中的高动态部分。

角加速度信号； 中值滤波； 离散小波阈值； 自适应

引 言

相对于角位移和角速度量，角加速度作为角运动高阶特性的表达，能够更快速、准确、直接地表征角运动。在航空航天、船舶武器、交通运输、地质探测及机器人结构分析等领域中，角加速度参数都有至关重要的作用及广泛的需求[1]。因此，为全面了解物体的运动状况，高精度、高可靠地获取角加速度信号具有十分重要的意义。

目前，角加速度信号的获取途径主要有直接法和间接法[2-3]。间接法又分为2种：a.对传统的角速率陀螺数据进行电子或电磁微分得到角加速度信号，但该方法会造成噪声放大和响应延迟，要求去除高频噪声的同时尽可能缩短信号的响应时间，因此难以得到可靠性高的角加速度信号；b. 运用多个线性加速度计组合间接求取角加速度[4]。有些载体如大机动状态下的战术导弹、高姿态抖动的新型小卫星及进行变负荷运转的机械臂[5]等，常常处于大过载、变负载、多扰动等复杂环境中，其角加速度信号往往呈现出高动态的特征。此方法需要先对线性加速度信号进行去噪和解算工作，计算量较大，求取精度和实时性也无法满足实际应用的需求。直接法则是采用可以直接敏感角加速度信号的传感器来测量，相比于间接法，采集到的角加速度信号可靠性及抗干扰能力更强，精度更高。笔者针对采用分子型液环式角加速度计[6]的测量信号开展去噪法的研究。文献[7]提出将Kalman滤波方法运用于角加速度信号估计。该方法适用于间接法测量的角加速度，按照位移、速度和加速度三者的微分关系对其建立状态方程，得到信号的最优估计。但Kalman滤波算法的局限性在于须得知系统的数学模型与噪声的先验统计知识，对于直接法获得的信号则难以获得角加速度传感器的数学模型，应用范围十分有限。文献[8]提出一种应用神经网络估计角加速度的算法，这种算法削弱了对系统模型的依赖，同时具有良好的自学习性、自组织性及高度适应性，但该方法需求的数据量巨大，算法实时性还有待进一步研究。文献[9]提出一种运用低通滤波器先对线加速度计信号去噪，再解算求取角加速度的方法，但此方法仅仅当噪声信号和原始信号的带宽完全分开时效果较好，无法用于高频振荡环境中的角加速度传感器。此外，受自身材料结构、载体机械振动及摩擦等复杂环境因素的限制，角加速度传感器信号中会带有大量混合种类的噪声，其中主要包括脉冲及高斯白噪声两类，采用单一的去噪算法并不能有效地去除混合噪声带来的影响。传统的中值滤波对于脉冲噪声的剔除效果较好，但该方法可能会破坏信号的细节信息[10]。由Donoho[11]提出的基于阈值的离散小波变换技术可以针对性地去除高斯白噪声，对处于高频震荡环境中的角加速度计能更精确地保留其信号中的有用细节。

针对上述问题，笔者提出一种基于改进的小波阈值与中值滤波相结合的角加速度计信号自适应去噪算法，并对仿真和实测信号的降噪效果与单一中值滤波算法、传统阈值小波去噪法进行分析和对比。

1 自适应小波去噪算法设计

在使用角加速度传感器时，电源电压的波动、载体的机械振动及摩擦、信号传输中的电磁干扰等因素都会对角加速度信号造成一定影响。这些噪声在时域中或是具有平坦的带宽特性，或是具有无规则的突发性，因此在研究时可看做是加性高斯白噪声和加性脉冲噪声。长度为的原始角加速度数字信号XN(t)如式(1)所示

XN(t)=S(t)+N1(t)+N2(t) (t=1,2,…，n)

(1)

其中：S(t)为真实角加速度信号；N1(t)为脉冲噪声信号；N2(t)为高斯白噪声信号。

对角加速度计信号进行去噪的目的是尽可能地将信号中的噪声成分N1(t)和N2(t)去掉，并尽可能精确地获得去噪后的估计信号S(t)。

1.1 中值滤波预处理

本算法先采用传统中值滤波法对原始角加速度带噪信号进行预处理，实现的具体方法[10]如下。

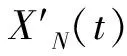
中值滤波算法的关键问题在于需要根据不同信号特征选取大小不同的滤波窗口。窗口选取过大，信号会丢失部分细节信息；反之，窗口过小会导致脉冲干扰剔除不够。由于角加速度信号可能会含有高频震荡的部分，为了能在有效平滑信号的同时，使预处理之后的信号尽可能保留有用的细节和能量，此处中值滤波窗口的选择应尽量偏小。通过实验测定，当选择窗口大小为5时，中值滤波算法去掉了大部分的脉冲噪声，预处理结果较好。该过程可以表示为

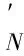
(2)

由于传统中值滤波窗口宽度通常为固定值，针对带有混合噪声的信号，此算法的自适应性和处理能力极为有限。因此，采用离散小波阈值去噪算法与中值滤波相结合可以取长补短，以达到更佳滤波效果。

1.2 离散小波阈值去噪

离散小波阈值去噪方法是目前应用最广泛的小波去噪方法之一[11[12-13]。笔者将重点研究分解层数的自适应确定及合理阈值的选取。

1.2.1 基于小波能量熵的自适应层数确定

离散小波阈值去噪法中，分解层数通常是对信号分解所得的细节系数进行白化检验[14]得到的。由于多扰动、大负载下的角加速度信号会具有与白噪声相关的高动态特性，此时无法简单对分解后的细节系数进行白化检验来区分真实信号与噪声信号。若从能量角度分析，对标准高斯白噪声序列用sym6小波进行1～9层分解，用式(3)计算出分解后1～9层细节系数的能量

(3)

其中：fj(t)为信号f(t)进行小波分解后第j层细节系数的幅值。

从图1可看出，白噪声信号细节系数的能量是随分解层数的增加而单调递减的。

图1 标准高斯白噪声信号细节系数的能量随分解层数的分布图Fig.1 The distribution of standards Gaussian white noise signal detail coefficients′ energy with the decomposition layers

对含白噪声在内的高动态角加速度信号进行小波分解后，细节系数中会因为包含这部分高动态信号，导致其1～9层的能量分布与单独白噪声信号分解的能量分布发生差异。因此，笔者根据最大熵原理[15]， 提出用小波能量熵(wavelet energy entropy，简称 WEE)更深刻地描述这种差异[16]，其计算公式为

其中：fi(t),i=1,2,…,M为信号进行M层离散小波分解后每层的细节系数；Pj为每层细节系数能量占细节系数能量总和的比例系数；Ej为每层细节系数的能量；j表示1～M层。

信号序列的复杂程度与其小波能量熵的值呈正相关关系，对比带噪信号和噪声信号在相同分解层数下的小波能量熵差异，通过设定此差异的阈值可自适应得出合理的分解层数。具体的计算步骤如下。

(6)

由此得到用来确定分解层数的信号样本XNsam，且其最大分解层数Mmax为9层。

2) 生成与XNsam长度相同的白噪声序列样本Nsam，并用式(7)对其进行归一化处理

(7)

3) 分别对信号X和N进行M=1层小波分解，由式(4)、式(5)可计算出X和N的1层小波能量熵WEEX(1)和WEEN(1)

4) 计算X与N进行M=1层离散小波分解所得分层能量熵的差

T=|WEEX(1)-WEEN(1)|

(8)

通过设定阈值来检测信号X和噪声N分层能量熵的明显差异来判断是否得到最佳分解层数，若T<0．2，则分解层数M加1，跳至步骤3继续进行离散小波分解；若T≥0．2则停止运算，并得到最终的最佳分解层数M0=M-1。

1.2.2 小波阈值的选取

硬阈值和软阈值函数[9]在小波阈值去噪领域已经得到广泛应用，其表达式为

(9)

其中：sgn(·)为符号函数。

关于阈值λ的选取，由Donoho提出了启发式SURE准则、严格SURE准则和极大极小准则。其中严格SURE准则和极大极小准则在去噪效果上较为保守，启发式SURE准则抑制噪声效果较好，但仍然可能丢失有用信息[11]。对此笔者提出一种新的阈值选取准则：利用中值滤波对细节系数中的噪声强度进行估计，并结合法则来设置门限阈值[14]。具体实现步骤如下。

2) 定义噪声的平均半宽度W，其值为噪声强度绝对值的均值，计算公式为

(11)

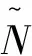
(12)

4) 求得门限阈值的下界与上界

(13)

按照门限阈值对小波系数采用硬阈值函数处理，进行一维离散小波逆变换即可得到去噪后的信号。

2 仿真分析

2.1 典型信号仿真分析

为验证本方法的优良性，本节着重体现自适应分解层数算法的有效性及阈值选择的合理性。以Matlab中Blocks，Doopler，Heavysine和Bumps这4种与角加速度计信号特征相似的非平稳随机信号进行仿真实验。如图2所示，信号长度均为2 048，在信号中叠加脉冲噪声和高斯白噪声以获得信噪比为5 dB左右的含噪信号。由图3可看到，由于噪声影响，各信号的细节部分已完全淹没在噪声中。

用窗口为3的中值滤波对信号进行预处理，选择同时具正交性和紧支撑性的sym6作为小波基函数对预处理后的信号进行离散小波分解，确定最佳分解层数分别为4层、5层、7层和5层。阈值处理函数均采用硬阈值函数，阈值准则分别采用通用阈值、启发式SURE准则、极大极小值阈值准则及笔者提出的阈值准则。

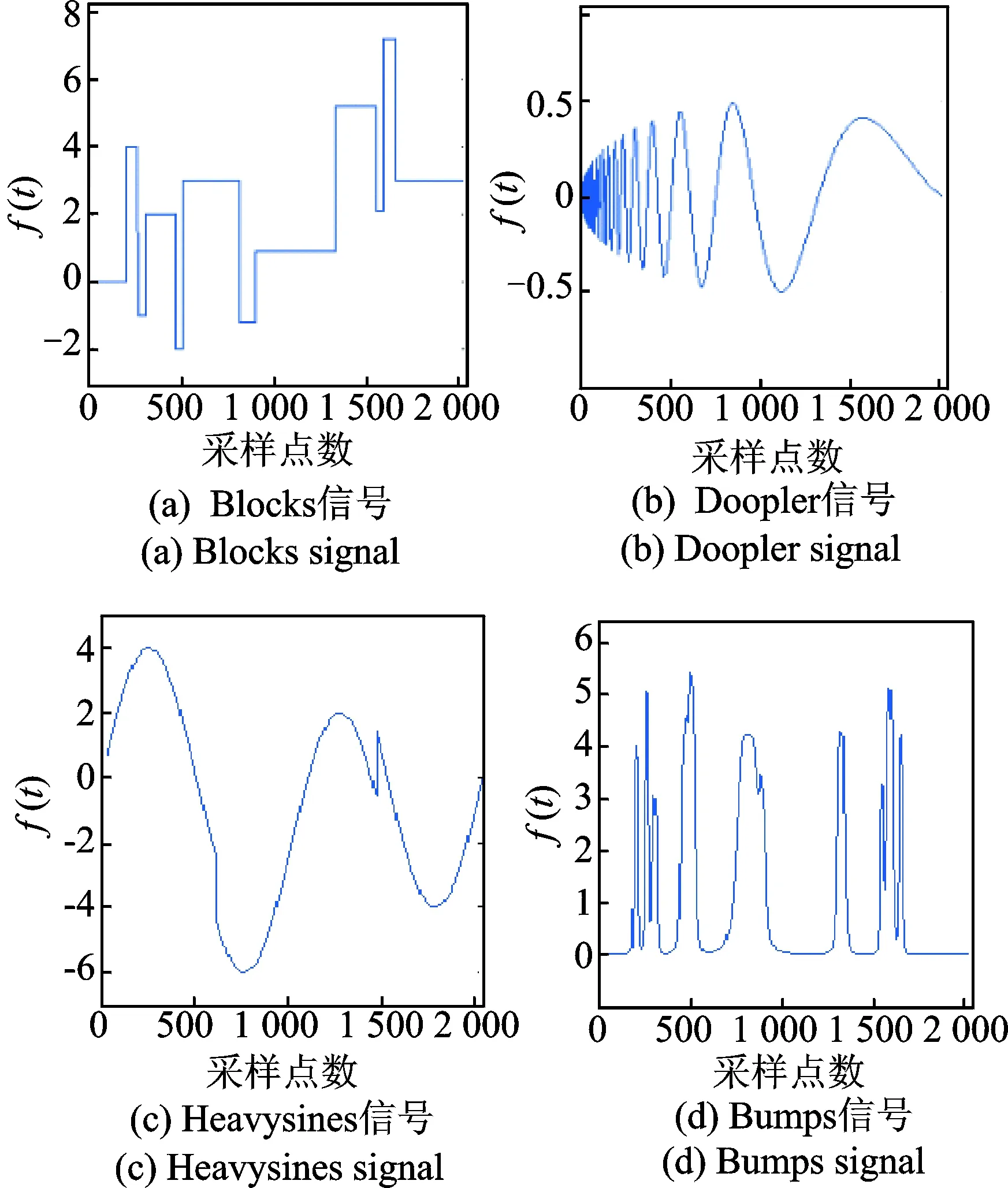
图2 Matlab中4种非平稳随机信号原始信号Fig.2 Four kinds of non-stationary random signal

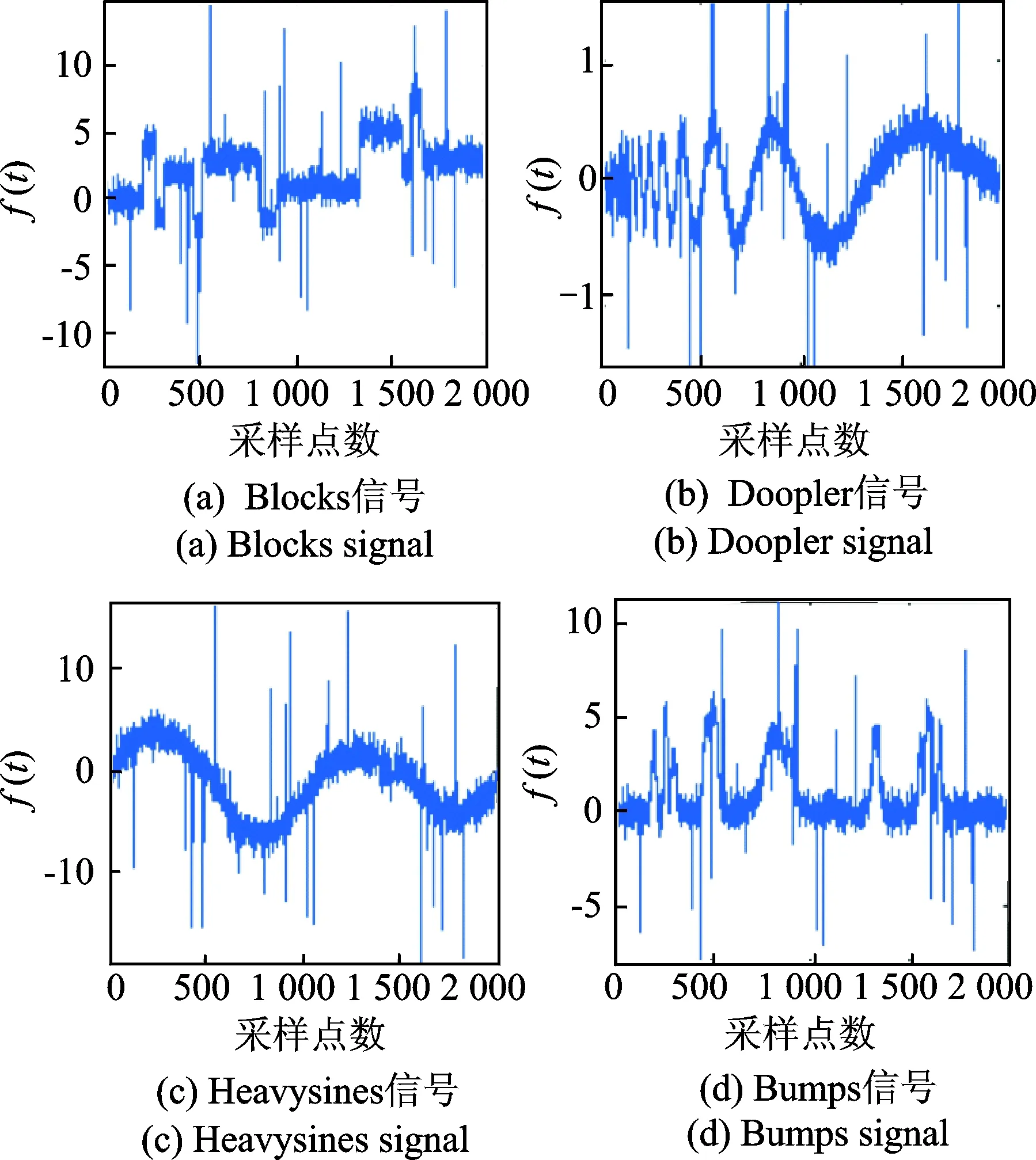
图3 信噪比为5 dB的4种仿真非平稳随机带噪信号Fig.3 Four kinds of simulation non-stationary random signal with noise that SNR is 5 dB

将4种信号按本算法得到的最佳分解层数进行降噪处理，采用信噪比(signal noise ratio，简称SNR)和均方根误差(mean square error，简称MSE)两项指标对去噪效果进行评估，并与最佳分解层数分别加1、减1的处理结果进行对比，结果如表1～4所示。由表中数据可知，对于不同信号，当分解层数未达到最佳时，信噪比同样未达到最佳。然而当分解层数超过最佳层数时，信号去噪后的信噪比或者会有较大下滑或者会平稳不变。考虑到分解层数增多会导致运算量加大和不稳定，因此该仿真结果可说明笔者提出的自适应分解层数确定的算法是有效的。

对比最佳分解层数下各阈值选取准则的去噪结果，可看到在使用通用阈值准则、极大极小阈值准则对Blocks，Bumps及Doopler信号进行处理时，信噪比没有提高反而降低了，最小均方误差也增大了；而笔者提出的阈值准则在最佳分解层数下针对4种仿真信号均能有效地提高信噪比，降低最小均方误差。由表中还可以看出，对于其他几种阈值准则，产生最大信噪比时对应的最佳分解层数发生了变化，这说明对于不同的信号，分解层数的确定及阈值准则的选取对于去噪效果的影响并不互相独立[17]，而笔者提出的自适应分解层数确定与阈值准则可以有机地结合在一起，从而得到最佳效果。

2.2 仿真效果比较

以Doopler信号为例，通过将本算法去噪结果与只对信号进行中值滤波去噪、只对信号进行小波降噪这两种方案进行对比，如图4所示，小波分解最佳层数为5层。从图中结果可以看出，只采用其中一种算法的降噪效果明显要差于将二者结合之后，说明本研究将中值滤波与离散小波阈值去噪法进行结合后可以得到比单一滤波效果更佳的降噪结果。

3 实验分析

3.1 低频转台实测信号分析

为验证本算法的实用性，对角加速度传感器实测信号进行实验分析，实验装置如图5所示。实验选用开放式中型双轴位置速率转台作为载体，并由转台控制系统设定输入信号的频率和幅值。选用分子型液环式角加速度计[3]来敏感测量载体的角加速度，并由嵌入式数字信号采集系统采集角加速度计输出信号。

表1 Blocks信号的处理结果

表2 Doopler信号的处理结果

表3 Heavysines信号的处理结果

表4 Bumps信号的处理结果

图4 本算法去噪结果与单一滤波方法去噪结果比较图Fig.4 De-noising results of propose algorithm compared with single filter method

首先给转台设定输入固定频率为1Hz、固定角速度为5 (°)/s的正弦激励信号。在测试过程中某些时刻对转台施加冲击，使角加速度计测量信号在对应时刻产生高动态变化，采集在该激励下的角加速度原始信号，并运用单一中值滤波算法、离散小波通用阈值去噪法及本算法对原始信号进行处理，实验结果如图6所示。

图5 实验装置图Fig.5 Experimental setup

图6 转台施加外部冲击测试结果Fig.6 Test results of turntable with attack

由实验结果可看出，当转台做低频运动时，载体机械摩擦、信号传输中的电磁干扰等噪声信号频率较高且幅值较小，而对转台施加干扰产生的高动态部分的信号频率、幅值都很高。因此，不论是中值滤波还是小波去噪法，在保留信号细节方面效果都较好；而在去除噪声平滑信号方面，本算法的优势较为明显。

3.2 无人车平台实测信号分析

将角加速度传感器及嵌入式数字信号采集系统安装在无人车车顶，测试并采集无人车行驶在沙石路况中得到的角加速度带噪信号，并运用单一中值滤波算法、离散小波通用阈值去噪法及本算法对该原始信号进行处理，实验结果如图7所示。

图7 无人车沙石路况测试结果Fig.7 Test results of driverless vehicle in gravel road

从结果中可以看到，由于无人车行驶在路况较差的沙石路段，车体颠簸较为明显，此时角加速度计信号整体呈现出高动态特征。采用单一滤波算法使得信号平滑度较好，但丢失了许多细节；采用通用阈值小波去噪算法在保留细节方面效果较好，但对于信号的去噪能力较差；本算法不仅可以有效去除角加速度信号中的噪声，同时能够很好地保留由负载产生的高动态部分。

4 结束语

通过对角加速度信号的获取及测量方式以及角加速度信号特征的分析，针对采用直接法获取到的角加速度计信号及其噪声特性，提出了一种采用中值滤波与离散小波阈值去噪法相结合的自适应降噪算法，并用于分子型液环式角加速度计信号的降噪处理中。通过仿真和实验分析，可以看到所提出的自适应降噪算法能有效提高信噪比，降低最小均方误差，在处理实测角加速度计信号中完整保留信号趋势和细节。

[1] 陆爱珍，林明邦，邹桂根.一种新的精密角加速度计[J].中国惯性技术学报，1991(2):87-92.

Lu Aizhen，Lin Mingbang，Zou Guigen. A new precision angular accelerometer[J]. Journal of Chinese Inertial Technology，1991(2):87-92. (in Chinese)

[2] 蔡艳萍，李艾华，胡重庆，等.平稳小波自适应去噪用于曲轴瞬时角加速度测量[J].振动、测试与诊断，2010, 30(6): 310-314.

Cai Yanping, Li Aihua, Hu Chongqing, et al. Measurement of instantaneous angular acceleration of crankshaft using adaptive stationary wavelet de-noising[J]. Journal of Vibration，Measurement & Diagnosis, 2010,30(6):310-314. (in Chinese)

[3] Ovaska S J，Valiviita S．Angular acceleration measurement： a review[J]．IEEE Transactions on Instrumentation and Measurement, 1998, 47(5): 1211-1217.

[4] Xiong Yonghu， Ma Baohua，Peng Xingping. Measurement of angular and linear accelerations using linear accelerometers[J]. Journal of Beijing Institute of Technology, 2000, 9(3):307-311.

[5] 吴校生，陈文元.角加速度计发展综述[J].中国惯性技术学报,2007,15(4):458-463.

Wu Xiaosheng，Chen Wenyuan. Review on angular accelerometer development[J]. Journal of Chinese Inertial Technology,2007,15(4):458-463. (in Chinese)

[6] 吴向荣，周蜜，孙荣凯，等.关于一种新型角加速度计的研究与应用[J].海军航空工程学院学报,2003,18(6):631-635.

Wu Xiangrong， Zhou Mi，Sun Rongkai，et al. An introduction to the research and application of a new type angular accelerometer[J]. Journal of Naval Aeronautical Engineering Institute, 2003,18(6):631-635. (in Chinese)

[7] Betanger P R，Dobrovolny P，Helmy A，et a1.Estimarion of angular velocity and acceleration from shaft encoder measurements[J]．International Journal of Robotics Research, 1998, 17(11):1225-1233．

[8] Gianfelici F. A novel technique for indirect angular acceleration measurement[C]∥IEEE International Conference on Computational Intelligence for Measurement Systems and Applications．Italy：Giardini Naxos,2005:120-123．

[9] Nehme N K，Chalhoub N G，Henein N A．Effects of filtering the angular motion of the crankshaft on the estimation of the instantaneous engine friction torque[J]. Journal of Sound and Vibration，2000，236(5):881-894.

[10] Wu Jin. Wavelet domain denoising method based on multistage median filtering[J]. Journal of China Universities of Posts & Telecommunications, 2013, 20(2):113-119.

[11] Donoho D L. De-nosing by soft-thresholding[J]. IEEE Transactions on Information Theory，1995，41(5): 613-627.

[12] 姜宏伟, 袁朝辉, 邱雷. 运用小波变换的飞机管路振动信号降噪方法[J]. 振动、测试与诊断, 2012, 32(5):827-830.

Jiang Hongwei，Yuan Chaohui， Qiu Lei. Wavelet transform based de-noising method on pipe vibration signals of aircraft[J]. Journal of Vibration，Measurement & Diagnosis, 2012(2):827-830. (in Chinese)

[13] 严鹏，李乔，单德山.斜拉桥健康监测信号改进小波相关降噪[J]. 振动、测试与诊断, 2012，32(2):317-322.

Yan Peng, Li Qiao, Shan Deshan. Improved wavelet correlation de-noising on cable-stayed bridge health monitoring signal[J]. Journal of Vibration ，Measurement & Diagnosis, 2012，32(2)：317-322. (in Chinese)

[14] 张吉先，钟秋梅，戴亚平.小波门限消噪法应用中分解层数及阈值的确定[J].中国电机工程学报, 2004, 24(2):118-122.

Zhang Jixian，Zhong Qiumei，Dai Yaping. The determination of the threshold and the decomposition order in threshold de-nosing method based on wavelet transform[J].Proceedings of the CSEE, 2004, 24(2): 118-122. (in Chinese)

[15] Jaynes E T. Information theory and statistical mechanics[J].Physical Review，1957，106: 620-630.

[16] Sang Yanfang，Wang Dong，Wu Jichun. Entropy-based method of choosing the decomposition level in wavelet threshold de-noising[J]. Entropy，2010，12:1499-1513.

[17] 丰彦，高国荣.小波阈值消噪算法中分解层数的自适应确定[J].武汉大学学报：自然科学版，2005,51(S2): 11-14.

Feng Yan， Gao Guorong. Self-adaptive determination of decomposition order inthreshold de-noising method based on wavelet transform[J]. Journal of Wuhan University：Natural Science Edition, 2005, 51(S2):11-14. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.06.012

国家自然科学基金资助项目(6142805,61473040)

2016-03-02；

2016-04-28

TP216.1；TP274.2；TH864

刘彤，男，1975年8月生，讲师。主要研究方向为组合导航与智能导航。曾发表《An optimization method for self-calibration method of dual-axis rotational inertial navigation system》(《Control Conference (CCC)》2013，Vol. 32)等论文。

E-mail：liutong2002@bit.edu.cn