基于振型多分辨复杂度谱的板结构损伤检测

徐宗美， 白润波,2， 张建刚， 刘传孝

(1.山东农业大学水利土木工程学院 泰安，271018) (2.河海大学力学与材料学院 南京，210098)

基于振型多分辨复杂度谱的板结构损伤检测

徐宗美1， 白润波1,2， 张建刚1， 刘传孝1

(1.山东农业大学水利土木工程学院 泰安，271018) (2.河海大学力学与材料学院 南京，210098)

针对目前基于振型的结构损伤检测方法普遍存在抗噪能力弱、对弱小损伤不敏感等不足，开展了克服这些缺陷的板类结构损伤识别研究。鉴于结构振型中噪声、趋势和损伤信息具有不同的尺度分布特性，基于二维高斯小波变换，提出多尺度振型空间概念，使振型的各成分信息得以独立表达，以凸显损伤信息。通过定义点态复杂度指标，借助滑动窗口法，在多尺度振型空间上形成多分辨复杂度谱。多分辨复杂度谱可使损伤进一步显现，能描述损伤的位置、大小及形状，并能反应损伤程度，实现了在噪声条件下对板类结构轻微损伤的准确表征。基于一实际工程闸门的数值模拟和两个模型试验，验证了所提方法的正确性和有效性。

损伤检测； 振型； 复杂度； 板； 二维高斯小波

引 言

结构物的损伤会降低结构的安全性，并可能引发灾害性突发事故。对结构进行损伤识别，特别是结构无损检测在世界范围内都得到了极大关注，成为当前土木水利、机械及航空航天等领域的研究热点问题之一。现有结构损伤识别方法中，基于结构振动响应的损伤检测技术由于理论明确、操作方便且对结构物无损害而获得了广泛研究应用。与其他振动响应参数相比，振型既是对结构整体力学特征的描述，又包含了结构局部的状态信息，具有实现结构损伤识别与工程预警的潜力。目前，基于结构振型及其衍生量已产生了很多结构损伤识别方法，如模态保证标准判别法[1]、坐标模态保证标准判别法[2]、振型曲率法[3]、应变能振型法[4]及振型小波变换系数法[5]等。随着科学技术的发展，一些现代量测设备，如扫描式激光测振仪等已可用来精确获得某些结构的振型，使上述方法具备了应用于实际工程损伤检测的可能。然而，现有方法普遍存在抗噪能力弱、对轻微损伤不敏感等不足[6-8]，有些方法还依赖于无损结构模型作参照[9-10]，这些都限制了结构损伤检测技术的实际应用。

为克服现有方法的弊端，笔者基于结构的损伤会引起结构振型局部复杂程度的改变这一认识[11-12]，以及振型中损伤、噪声和趋势成分信息跨尺度传播的不同特性[13-15]，提出尺度振型和多分辨复杂度物理量，并据此构建板结构振型的多分辨复杂度谱这一损伤识别指标。数值算例通过在一平面钢闸门的有限元模型上预设损伤，由闸门振型多分辨复杂度谱上的凸起来判定损伤的发生及其损伤位置、形状和尺寸。两个板构件的模型试验分别验证了多分辨复杂度谱对板类结构中线型裂缝损伤和面域块状损伤检测的适用性和有效性。

1 多分辨复杂度谱

1.1 尺度振型

实测结构振型信号中不可避免含有噪声，对板结构振型W: (x,y,w)，w表示采样点(x,y)处的振型幅值，损伤会引起W的局部奇异性，因此，定位损伤可通过定位W中的奇异性来获得。但轻微损伤引起的W奇异性微弱，一般难以直接观察到。一些文献将W从时域转换到频域进行研究，试图揭示W不同频段上的信息属性。据文献[13-15]所述，实测含损伤结构的振型在不同尺度频段上包含有3种信息成分：小尺度高频段上以噪声信号为主；大尺度低频段上以反应结构振动波形的趋势信号为主；中间一些频段上以损伤信息为主。振型的不同尺度特性可通过对振型进行小波变换得到

Ws:(x,y,ws)=W:(x,y,w)⊗ψs(x,y)

(1)

其中：ψs(x,y)为二维小波函数；s为尺度参数；⊗表示卷积；ws为尺度s下采样点(x,y)处的尺度振型幅值(s变化会引发一组尺度化的振型空间Ws: (x,y,ws)，原始振型是s趋近于0时尺度振型的特殊形式)。

与其他小波函数相比，二维高斯小波函数gs(x,y)具有对称性、平滑性、可微分及局部性等诸多适应损伤检测的特点[16-17]。笔者在对板结构振型进行尺度化时，选取gs(x,y)作为ψs(x,y)的一个优选形式

(2)

通过对板振型作高斯小波变换可分解得到一组尺度振型，在中间频段的某些尺度振型上，由于去除了大部分噪声和趋势成分，使损伤信息成分得以凸显。这种凸显有时还不足以被直接观察到，也没有明确的物理意义，而下面提出的多分辨复杂度物理量提供了描述这种局部奇异性的可能。

1.2 多分辨复杂度

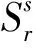
(3)

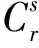
1.3 多分辨复杂度谱

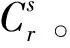
2 数值算例

平面钢闸门是水利枢纽中常用的开闭建筑物孔口的结构形式，其结构健康状况直接影响着水利枢纽能否正常运营。本节参照一实际工程平面钢闸门建立有限元模型，并假设其上存在线型损伤(如裂缝)和块状损伤(如腐蚀)两种形式，采用多分辨复杂度谱进行损伤定位和损伤程度度量。

2.1 含损伤闸门的有限元模型

某露顶式平面钢闸门的梁格布置如图1所示，在图1的A，B区格内预设一十字线型和一方形损伤。损伤采用降低刚度的方法模拟，对损伤处单元的弹性模量予以减少而质量保持不变，有Ed=(1-α)E，其中：E和Ed分别为损伤前后单元的弹性模量；α为损伤程度。本例考察了α=0.1，0.2，0.4这3种不同损伤程度的情况。闸门钢结构采用Q235-A·F，弹性模量E=210 GPa，泊松比ν=0.27，密度ρ=7 810 kg/m3。

采用有限元软件ANSYS建立闸门的有限元模型，闸门的面板采用SHELL63单元，闸门的主梁、次梁、边梁和底梁采用BEAM188单元。模型的底部采用竖向连杆约束，胶木滑块支撑处采用上下游方向连杆约束。整体有限元网格如图2所示。

考虑到闸门整体尺寸较大，而损伤仅存在于局部区域。为得到损伤位置周边较多的振动位移数据而不致使整体模型网格规模巨大，仅在A,B区格进行网格加密操作。A,B区格内的网格布置及损伤形式如图3所示，其中深色网格部分为发生损伤的单元，十字线型损伤的两条边长均为180 mm，方形损伤的边长为140 mm。这种对结构局部进行数据加密采集的操作在工程检测中具有重要现实意义：由于闸门尺寸较大而量测设备采样点数量有限，实际检测时，可将闸门分成几个区块，然后逐步量测每个区块的振动位移数据，进而对每个区块进行损伤检测。这样操作可以保证在有限的量测设备下尽可能地获得较精密的采样数据，避免了由于采样点过于稀疏导致的数据匮乏和结果粗糙。

2.2 模态振型及噪声施加

仅用闸门A,B区格范围内沿厚度方向的振动位移来作损伤检测，以任选的该区域某一模态振型为例进行分析。图4为固有频率66.2 Hz下损伤程度α=0.2时的模态振型W。由图4可见，仅从模态振型图上无法确定结构是否有损伤。

考虑到工程实际量测时不可避免含有噪声，损伤检测时，均在数值模态振型上加入信噪比SNR=50 dB的高斯白噪声以近似模拟真实的量测振型。

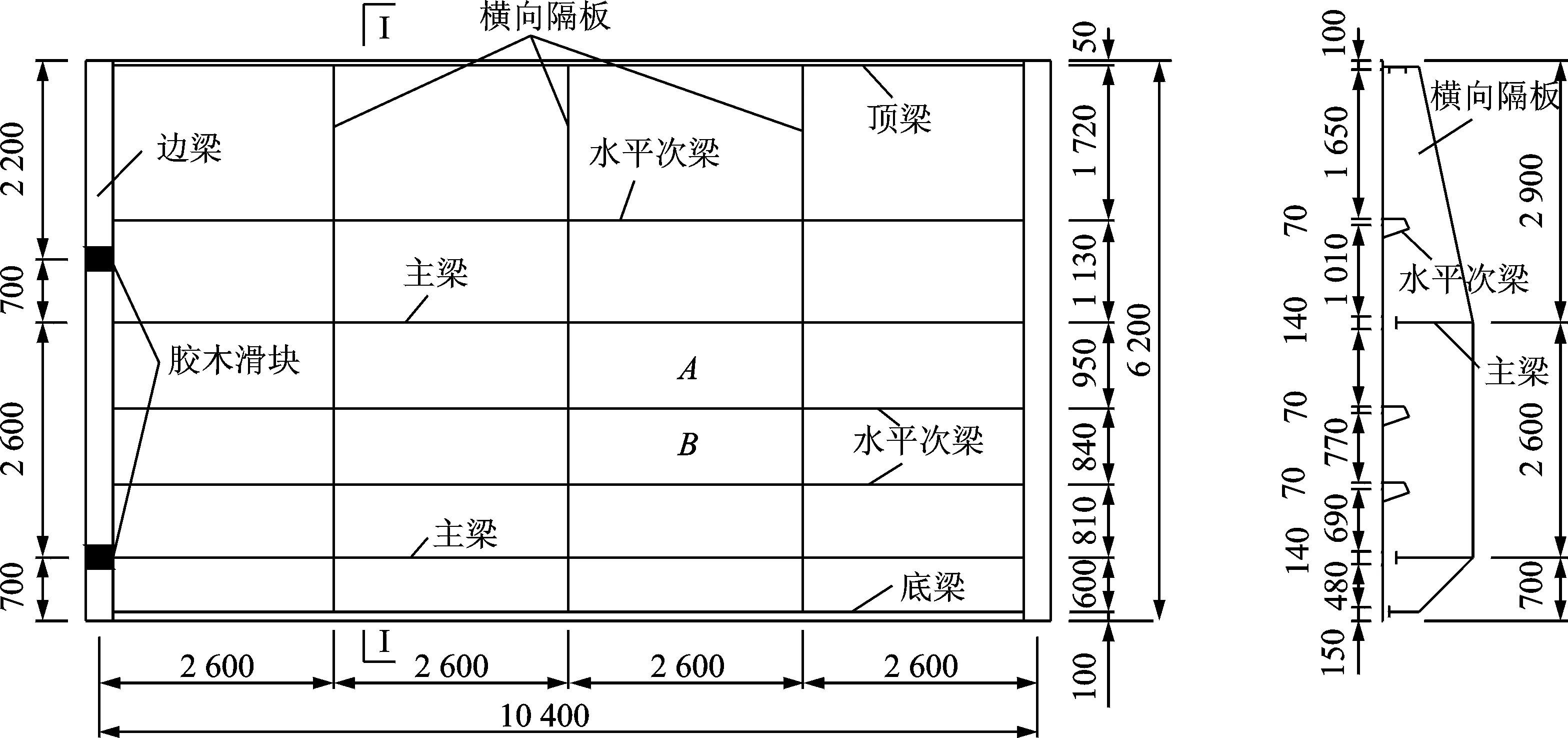
图1 闸门梁格布置图(单位：mm)Fig.1 Geometry of the hydraulic gate with stiff girder(unit: mm)

图2 闸门整体有限元网格图

Fig.2 Finite element model of the hydraulic gate

图3A,B区格网格细化及损伤布置 (单位：mm)

Fig.3 Refined mesh grid ofAandBarea with two type damage (unit: mm)

图4 固有频率66.2 Hz下A,B区格模态振型W

Fig.4 Mode shape at natural frequency of 66.2 Hz forAandBareas

2.3 损伤检测结果

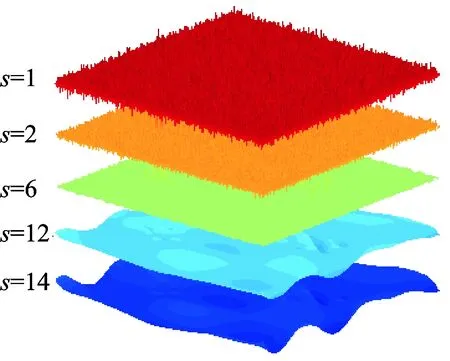
图5 W1, W2, W6, W12和W14Fig.5 W1, W2, W6, W12 and W14 of W

根据式(1)、式(2)对振型W作高斯小波变换得到一组尺度振型，按尺度参数s从小到大排列，代表性的尺度振型如图5所示。图中：s=1 和s=2的小尺度高频段上以噪声信号为主，表现为布满面域范围的不规则的众多小峰；s=12 和s=14的大尺度低频段上以趋势信号为主，表现为显示结构波动的振型轮廓；s=6的中间频段上，则显示出了损伤信息成分。以W6为分析对象，滑动窗口边长取r=4，按式(3)对W6进行逐点复杂度计算，得到图6所示的复杂度图Γ6。Γ6立体图中复杂度值大对应的凸起部分预示着该处可能存在损伤，从Γ6的平面图上可清晰地看到检测出的损伤位置、形状和尺寸，这与有限元模型中预设的损伤情况(图3)相吻合。多分辨复杂度谱检测出的是损伤的边界，如本例中Γ6在线型损伤和块状损伤的边缘有高的凸起，而损伤内部区域的复杂度值较小。

图6 α=0.2时的损伤检测图Γ6Fig.6 Identification of damage by Γ6 for α=0.2

图7 1-1截面图Fig.7 1-1 slices

不同损伤程度α下的检测效果与图6类似，但相应的多分辨复杂度计算值不同。图7为不同损伤程度下沿图6(b)1-1横断面所绘的Γ6的切片图，可见在α=0.1，0.2，0.4这3种情况下都能准确检测出损伤，且损伤处的多分辨复杂度峰值随着损伤程度的增大而增大，说明损伤程度增大会导致振型局部复杂程度的增加，多分辨复杂度谱在一定程度上能反应损伤程度的大小。

3 模型试验

为验证多分辨复杂度谱对板类结构损伤检测的适用性，做了两个模型试验。一个用于对线型损伤的检测，另一个用于对块状损伤的检测。

图8 铝板平面尺寸及划痕布置图(单位：mm)Fig.8 Geometry of the aluminum plate with a cross-like notch (unit: mm)

3.1 线型损伤检测试验

试件为一厚度4 mm的方形铝板，在铝板上刻划一“X”型交叉缝，划痕的每边长为40 mm，宽为1 mm，深为1 mm。铝板平面尺寸及划痕布置如图8所示。采用直径为10 mm的圆形压电陶瓷换能器(piezoceramic transducer，简称PZT)产生谐激励，由扫描式激光测振仪3D Polytec PSV-400量测板的振动模态。量测范围为图8中920 mm×920 mm的灰色区域，共包含451×449个均匀布置的采样点。

以试验测得的829 Hz激励下的振型W为例进行损伤检测。首先对W进行多尺度分解，观察各尺度振型的特点，注意到s=8时的W8已无很多杂乱毛刺和曲面波形，表示已去除了较多的噪声信息和趋势信息，为损伤信息的主要携带频段。对W8进行逐点复杂度计算，得到图9所示的复杂度图Γ8。Γ8立体图中复杂度值大处对应的凸起部分预示着该处可能存在损伤，凸起部分在Γ8平面图上对应着色彩亮度高的区域，清晰地显示了损伤的位置， 这与试验预设的损伤位置相吻合。Γ8检测出的是损伤的边界，这正是试验刻划的“X”型交叉缝的边界。

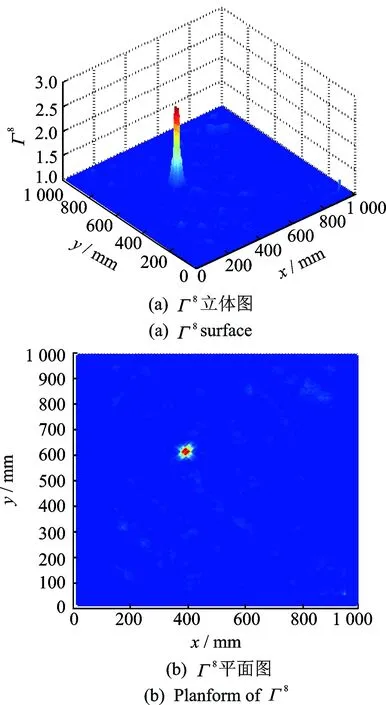
图9 铝板损伤检测图Γ8Fig.9 Identification of damage for the cracked aluminum plate by Γ8

3.2 块状损伤检测试验

试件为一厚度1.5 mm的方形玻璃纤维增强塑料(glass fiber-reinforced polymer, 简称GFRP)压层板，GFRP板厚度方向上由4层单向排列的玻璃纤维毡组成。在GFRP板局部用热风机以500℃温度持续6 s生成一微小局部分层。GFRP板平面尺寸及分层损伤位置如图10所示。同样采用PZT激励和3D Polytec PSV-400量测板的振动模态，共包含385×383个均匀布置的采样点。

图10 GFRP压层板平面尺寸及分层损伤位置图(单位：mm)Fig. 10 Geometry of GFRP plate with a small area of thermal delamination(unit: mm)

图11 GFRP压层板损伤检测图Γ8Fig.11 Identification of damage for the delaminated GFRP plate by Γ8

以试验测得的1 264 Hz下的振型W为例进行分析。通过对W作高斯小波变换得到一组尺度振型，观察到在s=8时去除了较多的噪声信息和趋势信息。对W8进行逐点复杂度计算，得到图11所示的复杂度图Γ8。Γ8立体图中复杂度值大处对应的凸起部分预示着该处可能存在损伤，凸起部分在Γ8平面图上对应着色彩亮度高的区域，清晰地显示了损伤的位置、形状和尺寸，这与试验预设的分层损伤情况相吻合。

4 结束语

借助小波变换将振型分解为多尺度振型空间，传统振型是多尺度振型在尺度趋近于0时的特殊形式。从损伤检测角度，鉴于结构振型信号中噪声、趋势和损伤信息具有不同的尺度分布特性，多尺度振型空间提供了各成分信息独立表达的机制，在一些特定的尺度振型上可以使损伤信息凸显，为噪声条件下轻微损伤检测创造了条件。

复杂度的定义使尺度振型空间下的凸显有了明确的物理意义。多分辨复杂度谱可使损伤进一步显现，能描述损伤的位置、形状及尺寸，并能定性反应损伤程度。多分辨复杂度谱的损伤检测方法不依赖于无损基准模型，实现了噪声条件下对板类结构轻微损伤的准确表征。数值算例和模型试验验证了本研究方法的正确性和有效性。

[1] 安永辉，欧进萍. 简支梁桥损伤程度识别的模拟和试验[J]. 振动、测试与诊断，2013，33(1)：60-65.

An Yonghui, Ou Jinping. Experimental and numerical studies on damage severity identification of simply supported beam bridges[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(1)：60-65. (in Chinese)

[2] Balsamo L, Mukhopadhyay S, Betti R, et al. Damage detection using flexibility proportional coordinate modal assurance criterion[C]∥Topics in Modal Analysis．New York： Springer, 2014:1-8.

[3] 徐华东，王立海，胡志栋. 运用曲率模态技术的木梁损伤定量识别[J]. 振动、测试与诊断，2011，31(1)：110-114.

Xu Huadong, Wang Lihai, Hu Zhidong. Quantitative identification of wood beam damage using modal curvature theory[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(1)：110-114. (in Chinese)

[4] 黄立新，杨真真，赵文举. 基于模态应变能变化率法的 Euler-Bernoulli 功能梯度梁的损伤识别[J]. 玻璃钢/复合材料，2015，8:14-17.

Huang Lixin, Yang Zhenzhen, Zhao Wenju. Damage identification of Euler-Bernoulli functionally graded beam by the modal strain energy change ratio method[J]. Fiber Reinforced Plastics/Composites, 2015, 8:14-17. (in Chinese)

[5] 丁科. 曲率模态小波分析在桥梁损伤检测中的应用[J]. 噪声与振动控制，2013，33(5)：131-135.

Ding Ke. Application of wavelet analysis of curvature modal to damage detection of bridges[J]. Noise and Vibration Control, 2013，33(5)：131-135. (in Chinese)

[6] 刘国华，谢中凯. 一种用于检测梁结构损伤的改进传递熵[J]. 振动工程学报，2014，27(1)：136-144.

Liu Guohua, Xie Zhongkai. A modified transfer entropy method for damage detection of beam structures[J]. Journal of Vibration Engineering, 2014, 27(1): 136-144. (in Chinese)

[7] Bai R B, Cao M S, Su Z, et al. Fractal dimension analysis of higher-order mode shapes for damage identification of beam structures[J]. Mathematical Problems in Engineering, 2012, 2012:454568.

[8] 刘才玮，张毅刚，吴金志. 基于动力测试的单层柱面网壳损伤定位与试验研究[J]. 土木工程学报，2014, 47(6)：9-17.

Liu Caiwei, Zhang Yigang, Wu Jinzhi. Experimental study on damage location of single-layer latticed cylindrical shell based on the dynamic testing[J]. China Civil Engineering Journal, 2014, 47(6): 9-17. (in Chinese)

[9] Cao M S, Ostachowicz W, Bai R B, et al. Fractal mechanism for characterizing singularity of mode shape for damage detection[J]. Applied Physics Letters, 2013, 103(22):221906.

[10] 邱飞力，张立民，张卫华. 改进的特征值灵敏度在结构损伤识别中的应用[J]. 振动、测试与诊断，2016，36(2)：264-268.

Qiu Feili, Zhang Limin, Zhang Weihua. Structure damage detection based on improved eigen value sensitivity[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(2): 264-268. (in Chinese)

[11] 朱宏平，余璟，张俊兵. 结构损伤动力检测与健康监测研究现状与展望[J]. 工程力学，2011，28(2)：1-11.

Zhu Hongping, Yu Jing, Zhang Junbing. A summary review and advantages on vibration-based damage identification methods in structural health monitoring[J]. Engineering Mechanics, 2011, 28(2):1-11. (in Chinese)

[12] Bai R B, Song X G, Radzieński M, et al. Crack location in beams by data fusion of fractal dimension features of laser-measured operating deflection shapes[J]. Smart Structures and Systems, 2014, 13(6): 975-991.

[13] Bai R B, Ostachowicz W, Cao M S, et al. Crack detection in beams in noisy conditions using scale fractal dimension analysis of mode shapes[J]. Smart Materials and Structures, 2014, 23(6):065014.

[14] Masoumi M, Ashory M R. Damage identification from uniform load surface using continuous and stationary wavelet transforms[J]. Latin American Journal of Solids and Structures, 2014, 11: 738-754.

[15] Xu W, Radzieński M, Ostachowicz W, et al. Damage detection in plates using two-dimensional directional Gaussian wavelets and laser scanned operating deflection shapes[J]. Structural Health Monitoring, 2013, 12(5-6): 457-468.

[16] Bai R B, Radzieński M, Cao M S, et al. Non-baseline identification of delamination in plates using wavelet-aided fractal analysis of two-dimensional mode shapes[J]. Journal of Intelligent Material Systems and Structures, 2015, 26(17)：2338-2350.

[17] Jiang X, John Ma ZG, Ren W X. Crack detection from the slope of the mode shape using complex continuous wavelet transform[J]. Computer-Aided Civil and Infrastructure Engineering, 2012, 27(3): 187-201.

10.16450/j.cnki.issn.1004-6801.2017.06.030

国家自然科学基金资助项目(51508156)；中国博士后科学基金资助项目(2014M560386)；山东省自然科学基金资助项目(ZR2014EL034)

2015-11-21；

2016-06-12

TH113.1； TB123

徐宗美，女，1980年4月生，博士生、讲师。主要研究方向为结构损伤检测。曾发表《Singularity detection of 2D signals using fractal dimension analysis of scale information》(《Journal of Vibroengineering》2016, Vol.18,No.2)等论文。

E-mail: xuzongmei_1999@126.com

(第37卷卷终)