罕遇地震下自定心支撑张弦桁架振动响应分析
2018-01-04朱冬平刘德军
曾 滨, 周 臻, 朱冬平, 刘德军
(1.中冶建筑研究总院有限公司 北京,100088)(2.东南大学混凝土及预应力混凝土结构教育部重点实验室 南京,210096)
罕遇地震下自定心支撑张弦桁架振动响应分析
曾 滨1, 周 臻2, 朱冬平2, 刘德军1
(1.中冶建筑研究总院有限公司 北京,100088)(2.东南大学混凝土及预应力混凝土结构教育部重点实验室 南京,210096)
针对带自定心耗能支撑张弦桁架在罕遇地震作用下的振动响应,将自定心耗能支撑与大跨张弦桁架结构相结合,利用有限元软件建立单榀带自定心耗能支撑张弦桁架的分析模型,采用弹塑性时程分析研究结构在罕遇地震激励下主桁架结构屈服时的振动响应。分析结果表明,自定心耗能支撑能够改善结构的振动特性,可有效减小结构震后残余变形。研究了自定心耗能支撑的启动力、启动位移和强度比等关键滞回参数对结构振动响应的影响,结果表明:增大支撑启动力可以有效控制水平方向的残余变形;减小支撑强度比可以增强自复位能力,但会降低支撑自身耗能能力;启动位移对结构峰值位移有一定影响,对残余变形影响较小,但当启动位移过大时,支撑的自复位能力会有所降低。
张弦桁架;自定心;耗能支撑;有限元分析
引 言
张弦结构是由上弦受弯受压构件与下弦拉索通过撑杆形成的自平衡受力体系[1],其最初形式采用Saitho等[2]提出的张弦梁结构。随着结构跨度的增大,张弦梁上部构件内力增大,为了提高结构的经济性和承载能力,将上部的实腹式梁更换为管式桁架,从而形成了张弦桁架结构[3-4]。
随着张弦桁架在各类大型公共建筑的广泛应用,其在强震作用下的安全性和震后修复问题日益受到重视。目前,对于张弦桁架的研究主要集中于其结构设计分析[5]、优化设计[6]以及抗倒塌分析[7]等方面,对其减震的研究相对较少。近年来,自定心耗能支撑(self-centering energy dissipative brace, 简称SCEDB)由于兼具良好耗能能力和残余变形控制能力,已经被广泛研究和使用。Christopoulos[8]通过在内外套筒中张拉预应力芳纶纤维形成自定心系统,并在自定心耗能支撑的内外套筒间引入摩擦耗能装置,从而使得自定心支撑能够进行耗能。Miller等[9]将形状记忆合金(shape memory alloy, 简称SMA)与自定心屈曲约束支撑(self-centering buckling restrained brace,简称SC-BRS)相结合,构成带形状记忆合金的自定心屈曲约束支撑(SMA-SC-BRS)并进行相应的试验,结果表明这种支撑的耗能和复位能力较好。谢钦等[10]将SMA的本构与流变模型进行结合,构建了一种分析SMA-SC-BRB的流变分析方法。在其抗震性能方面,Tremblay等[11]对安装有自定心耗能支撑的框架进行时程分析和pushover分析,结果表明相对于安装有BRB的框架,安装有自定心耗能支撑的框架在达到相同的地震动水准下具有较小的残余位移角。笔者将SCEDB引入张弦桁架中,研究其在双向(水平和竖向)罕遇地震激励下结构的振动响应,并分析SCEDB滞回参数对张弦结构减震效果的影响。
1 分析模型
1.1 张弦桁架模型
图1所示为某张弦桁架结构单榀的分析模型。结构支座采用一端(A点)固定铰支座,一端(B点)滑动支座。模型中跨为80.75m,两端分别悬挑18.25m和16.50m。上弦桁架采用平滑连接的3段圆弧组成,宽为4m,高为2.49m。下弦拉索线型为近似抛物线型,矢高为4m。中间均匀布置7根撑杆,撑杆间距为10.22m,撑杆高度有4种尺寸,依次为2.6,5.4,7.4和8.00m。杆件均采用圆形截面钢管,材质为Q345钢材。拉索采用直径为7mm的塑料护套半平行钢丝索,抗拉强度为1 570MPa。结构主要杆件截面规格见表 1。
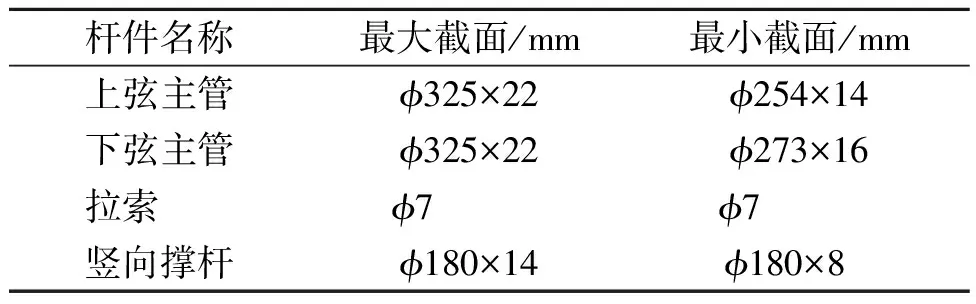
表1 结构主要构件截面规格
利用有限元软件ANSYS建立分析模型,由于要进行结构在罕遇地震作用下的弹塑性时程分析,张弦桁架构件可能屈服,因此材料模型采用理想弹塑性,考虑为双线性随动强化准则。上部张弦桁架中采用BEAM188单元模拟弦杆;腹杆以及结构的竖向撑杆采用7根LINK8单元进行模拟;而预应力筋拉索由于不考虑受压,可以采用8根LINK10只拉单元进行模拟。本研究采用单榀结构分析,因此分析时,在实际工程中的横向檩条处施加平面外约束。在支座A点约束所有位移自由度,在B点约束z向和x向自由度。原结构在使用阶段的荷载等效为质量附加于节点上。预应力采用降温方式施加,荷载值为100kN。
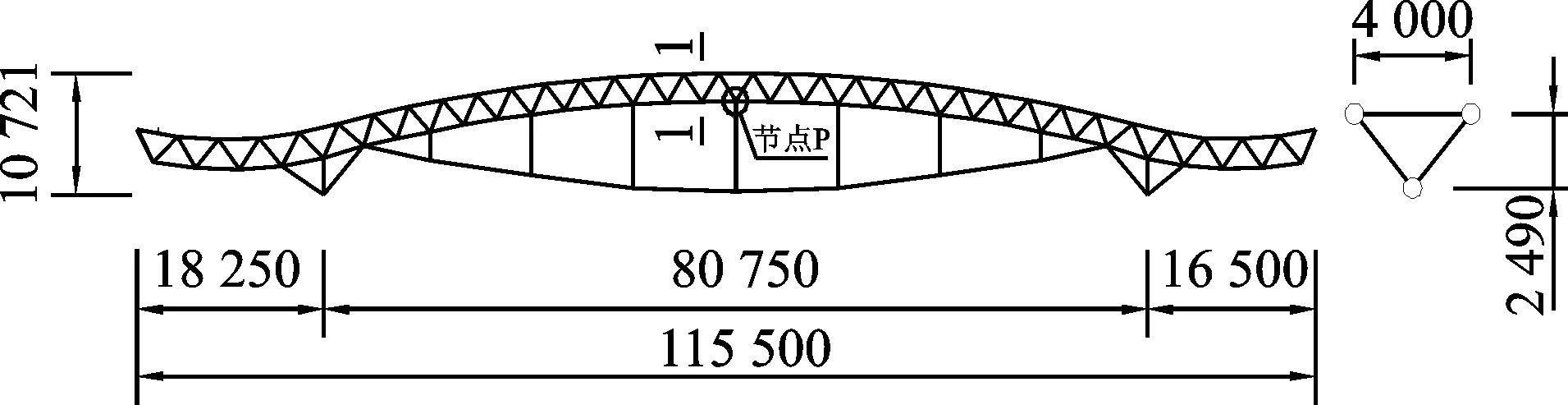
图1 单榀张弦桁架分析模型(单位:mm)Fig.1 Schematic diagram of cable-supported truss(unit:mm)
1.2 自定心耗能支撑的模拟
图 2给出了圆管截面的SCEDB构造示意,其基本部件由内套管、外套管、预应力筋及摩擦耗能件组成。摩擦耗能件设置在内、外套管之间,利用支撑变形过程中产生的相对运动耗能。在内、外套管的端部增加端板,并在两端端板之间增设预张拉的预应力筋,为支撑提供稳定的自复位力,使支撑在外荷载消失后仍能自动复位[8]。
在地震过程中,支撑承受往复拉压荷载,其基本受力过程为:当支撑所受外力小于摩擦力和预应力筋初张力之和时,支撑不会发生变形;当所受外力超过初张力和摩擦力之和时,支撑内外套管会发生相对位移,此时摩擦装置启动并耗能,而预应力筋则无论支撑处于受压状态还是受拉状态其均为受拉状态,为整个支撑提供自复位能力。因此,SCEDB的滞回曲线具有典型的旗帜型特征[10-12],见图 3(a),其中:Sy为支撑启动位移;Fy为支撑启动力;k1为支撑第1刚度;k2为支撑第2刚度。
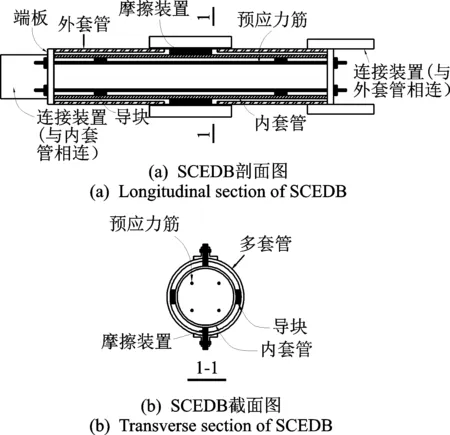
图2 圆管式SCEDB构造示意Fig.2 Schematic diagram of SCEDB
由于在ANSYS中没有自定心耗能单元,因此可采用自定心单元与耗能单元并联来模拟。其中,自定心单元采用图3(b)所示的具有双线性弹性材料的拉压杆,耗能单元采用图3(c)所示的具有理想弹塑性材料的拉压杆。定义支撑强度比β为支撑中摩擦装置摩擦力Fd与弹性材料强化力Fe之比
β=Fd/Fe
(1)
要保证结构的自复位能力,则β取值应小于1。
在进行分析时保证两种材料具有相同的启动位移Sy。由于支撑长短不同,为保证支撑在罕遇地震下能够工作,可以控制支撑具有相同的启动力,因此设置较短支撑启动位移为3.2mm,启动力为103.5kN;较长支撑启动位移为3.5mm,启动力为103.5kN。
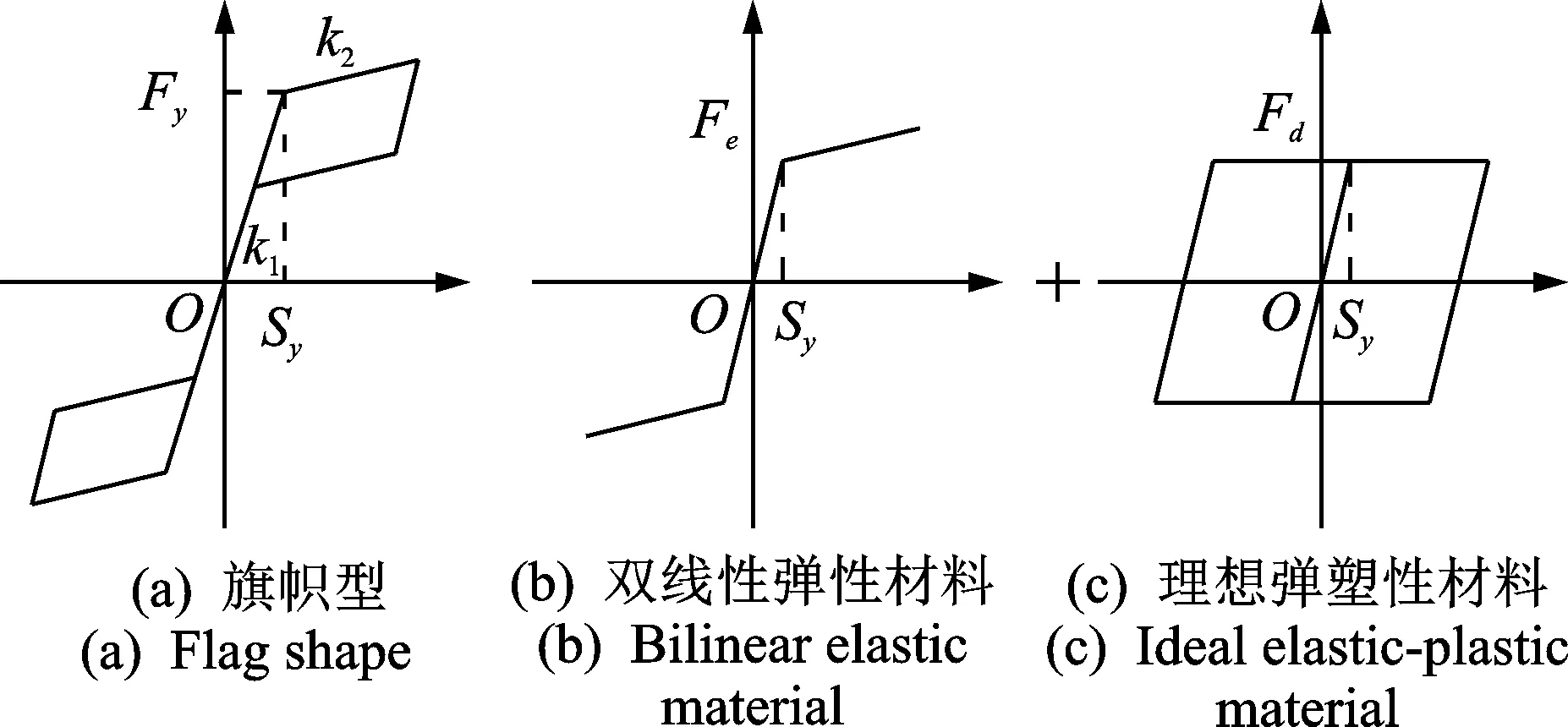
图3 自复位支撑本构曲线Fig.3 Hysteretic curve of SCEDB
为使SCEDB耗能作用充分发挥,应尽可能将其布置于相对变形差较大的位置。因此,笔者分析时,将SCEDB设置于靠近支座的上弦桁架与下弦拉索之间,并采用左右对称布置,如图 4所示。

图4 自定心耗能支撑布置示意Fig.4 Arrangement type of SCEDB
2 时程分析
首先进行结构自振分析,前4阶振型见图 5,自振频率计算结果见表 2。可以看出,支撑的增加改变了结构的固有频率,并使结构的振型发生改变。
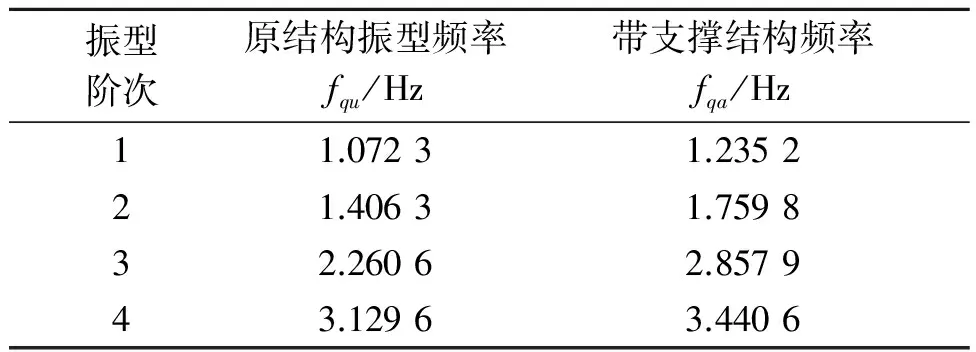
表2 结构自振频率
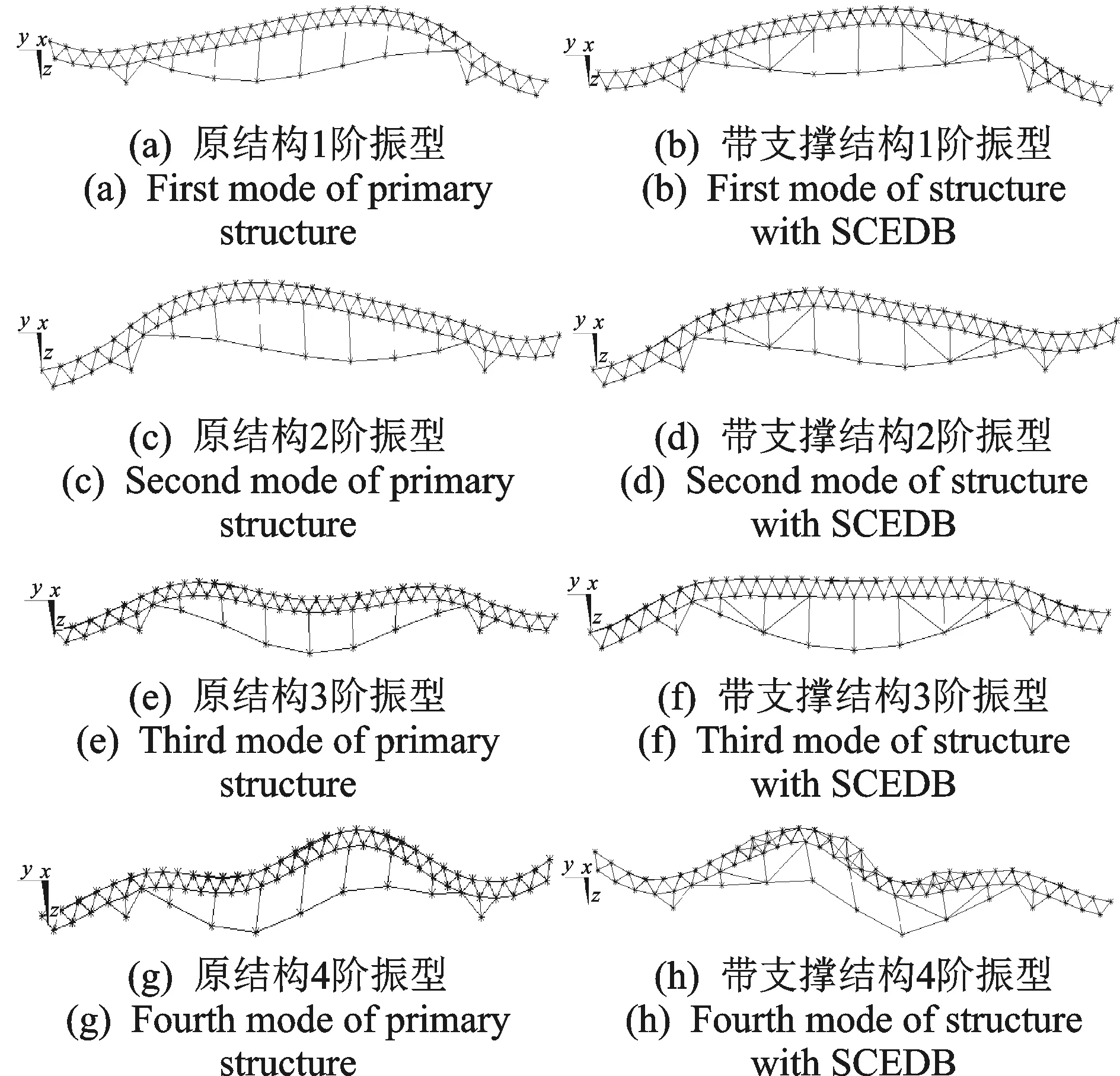
图5 原结构与带支撑前4阶振型Fig.5 First four structure modes of vibration
时程分析中假定结构阻尼比ζ=0.02,采用考虑瑞雷阻尼(比例)。分析采用El Centro地震波,加速度峰值为3.12m/s2,同时施加水平地震波和竖向地震波。根据GB50011-2010《建筑抗震设计规范》规定,竖向地震强度按水平地震强度的65%进行调幅。为考察在罕遇地震激励下桁架屈服后自定心耗能支撑的作用,将地震幅值增加5倍。分析过程分两步:a.首先考虑预应力和使用荷载作用;b.在此基础上施加地震加速度激励。
图 6给出了上弦桁架跨中下节点P在El Centro地震波作用下的时程曲线。由图 6可以看出,在罕遇地震作用下,原张弦桁架将会出现较大震动幅度,并且震后出现较大的残余变形。其中在水平方向桁架振幅接近0.43m,竖直方向接近0.53m。原结构的残余变形也较大,水平方向达到0.10m,竖直方向为0.28m。当结构增加自定心耗能支撑后,结构水平方向负向最大幅值与原结构相同,但结构振动接近于初始平衡位置,且残余变形得到有效的控制,其水平方向残余变形为0.06m,减小了40%。在竖直方向,结构正向振幅由0.44m减小为0.36m,并且残余变形减小为0.21m,减小了25%。
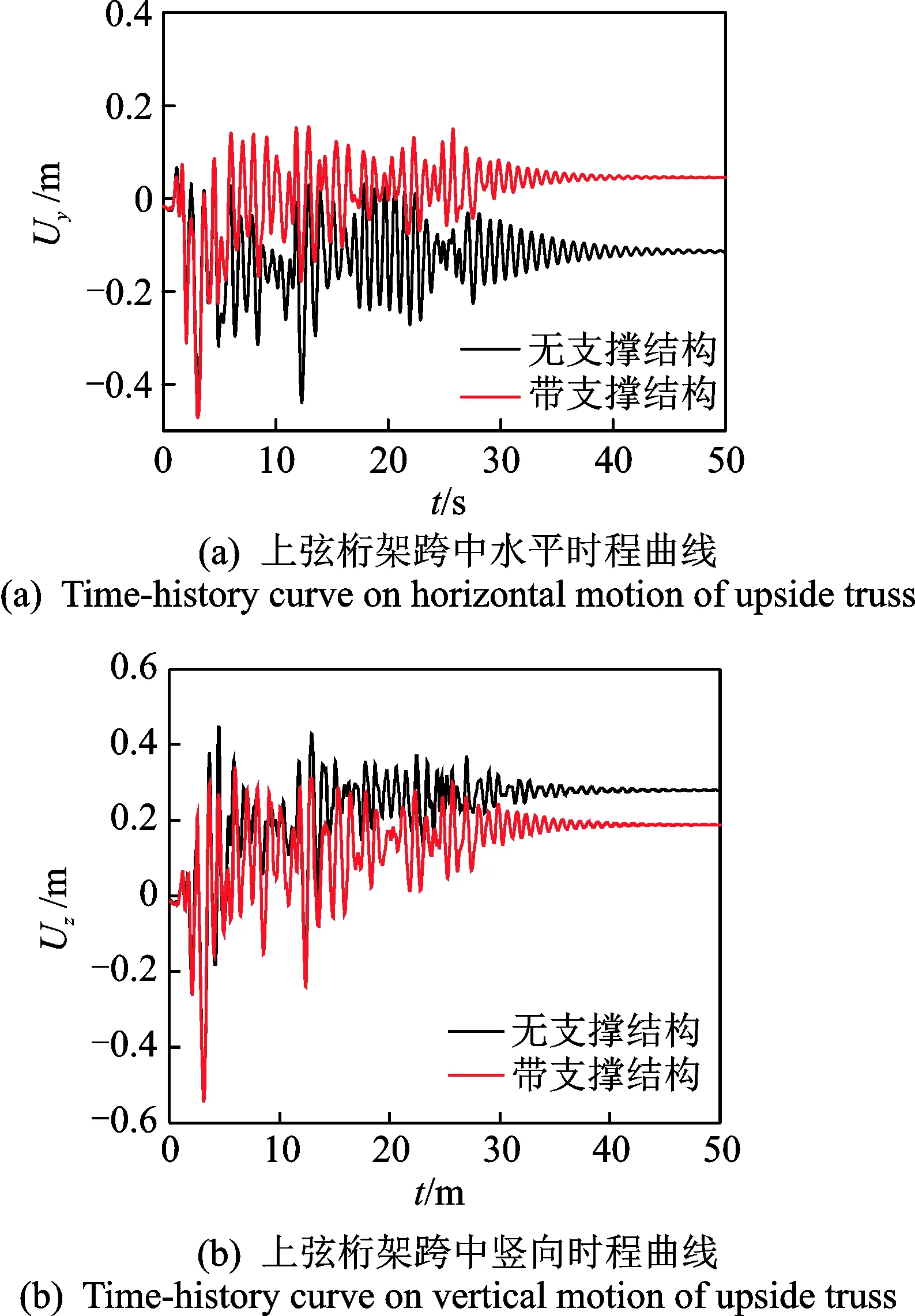
图6 结构时程曲线对比Fig.6 Comparison of time-history curve
图7给出模型中模拟自定心耗能支撑的2根拉压杆应力-应变的叠加曲线,由于2根杆件具有相同的面积,因此可以直接将二者相加。从图中可以看出,在地震波激励的过程中,支撑整体滞回曲线呈旗帜型,且具有较大的滞回面积,在结构中起到复位耗能的作用。在增加自定心耗能支撑的张弦桁架中,由于自定心耗能支撑的作用,可以使得结构在罕遇地震作用下尽可能处于初始位置附近振动,改善结构振动特性,并减小结构的残余变形。
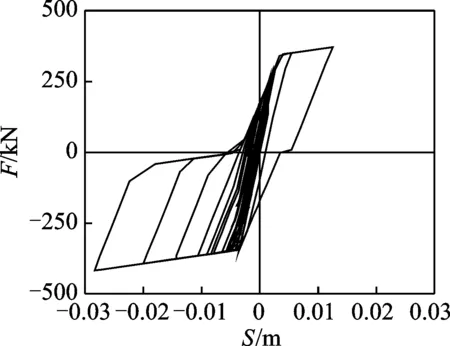
图7 自定心耗能支撑滞回曲线Fig.7 Hysteretic curve of SCEDB
3 参数化分析
根据自定心耗能支撑特征,对自定心耗能支撑的参数进行变化,分析其对张弦桁架减震的影响。
3.1 启动力
在保证材料属性一定的情况下,自定心耗能支撑的启动力Fy决定支撑何时进入耗能阶段。较小的启动力可以使得支撑尽快进入耗能阶段,但是支撑整体的滞回面积将会变小,支撑耗能会降低;较大的启动力可能会使支撑一直处于弹性状态。因此在实际结构中,自定心耗能支撑的启动力要经计算得到。笔者调节支撑启动力由小变大,分析其对于结构的影响。
图 8给出了自定心耗能支撑启动力对于结构跨中振幅以及残余变形的影响,设置模型中的拉压杆截面积变化控制其启动力。当Fy=0时则表示拉压杆截面积为零,即不增加自定心耗能支撑。从图 8(a)可以看出,自定心耗能支撑的启动力与水平方向的振幅(PUY)影响不大;但是随着启动力的增大,竖直方向的振幅(PUZ)先增加后减小,即在Fy=138kN时达到最大值,之后随着启动力增加逐渐减小。这主要与支撑布置形式有关。根据图 5所示的结构振型可以看出,在支撑布置后,局部区域反而会出现位移增大的情况。图 8(b)给出了结构的残余变形与自定心耗能支撑启动力之间的关系曲线,从图中可以看出,增加支撑后竖向残余变形(RUZ)立即减小,但与支撑的启动力关系不大,残余变形降幅保持在约36%;其水平方向残余变形(RUY)可以通过调节支撑启动力使其基本为零。
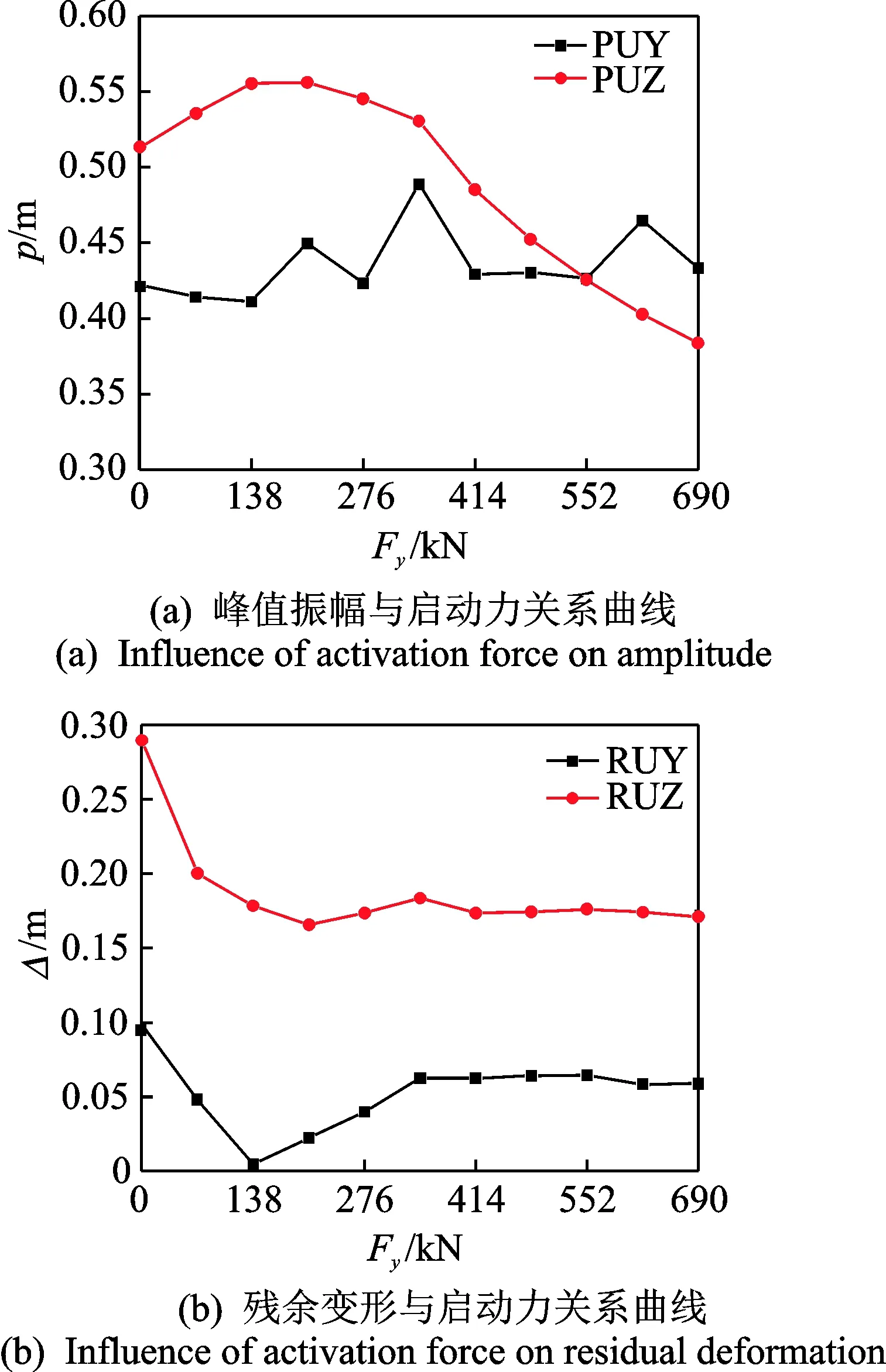
图8 自定心耗能支撑启动力影响曲线Fig.8 Influence curve by different activation force of SCEDB
因此,调节自复位耗能支撑的启动力可有效减小结构残余变形,结构水平方向的残余变形可以减小为零,竖直方向残余变形可以减小36%左右。
3.2 支撑强度比
在自定心耗能支撑中通过调整预应力筋的参数值以及相应的摩擦装置设置支撑的恢复能力以及耗能能力。定义支撑强度比α为支撑中摩擦装置摩擦力Fd与总启动力Fy之比,即
α=Fd/Fy=β/(1+β)
(2)
为满足支撑自定心的要求,α值要求小于0.5。通过控制α值可以在保持总启动力不变的情况下控制支撑的滞回面积以及残余变形,因此本节将在保持支撑总启动力不变的情况下,改变α值,分析其对结构在地震作用中的振幅及残余变形的影响。
图9给出了张弦桁架跨中的峰值振幅以及残余变形与结构自定心耗能支撑强度比关系曲线。由图 9(a)可以看出,在α增大后,水平方向的振幅出现一定的波动,但变幅不大;竖直方向的峰值振幅在α值为0.5时达到最大,相对于α=0.4时扩大了14%。这表明支撑耗能的增加并不一定会减小结构的振幅,这与振型分析结果相吻合。由图 9(b)可以看出,在α增大后,水平方向与竖直方向的残余变形具有相同的变化趋势,当α增加到较大值时,其残余变形也会增加,这与支撑在增加摩擦耗能之后,其恢复力下降,残余变形增大有关。
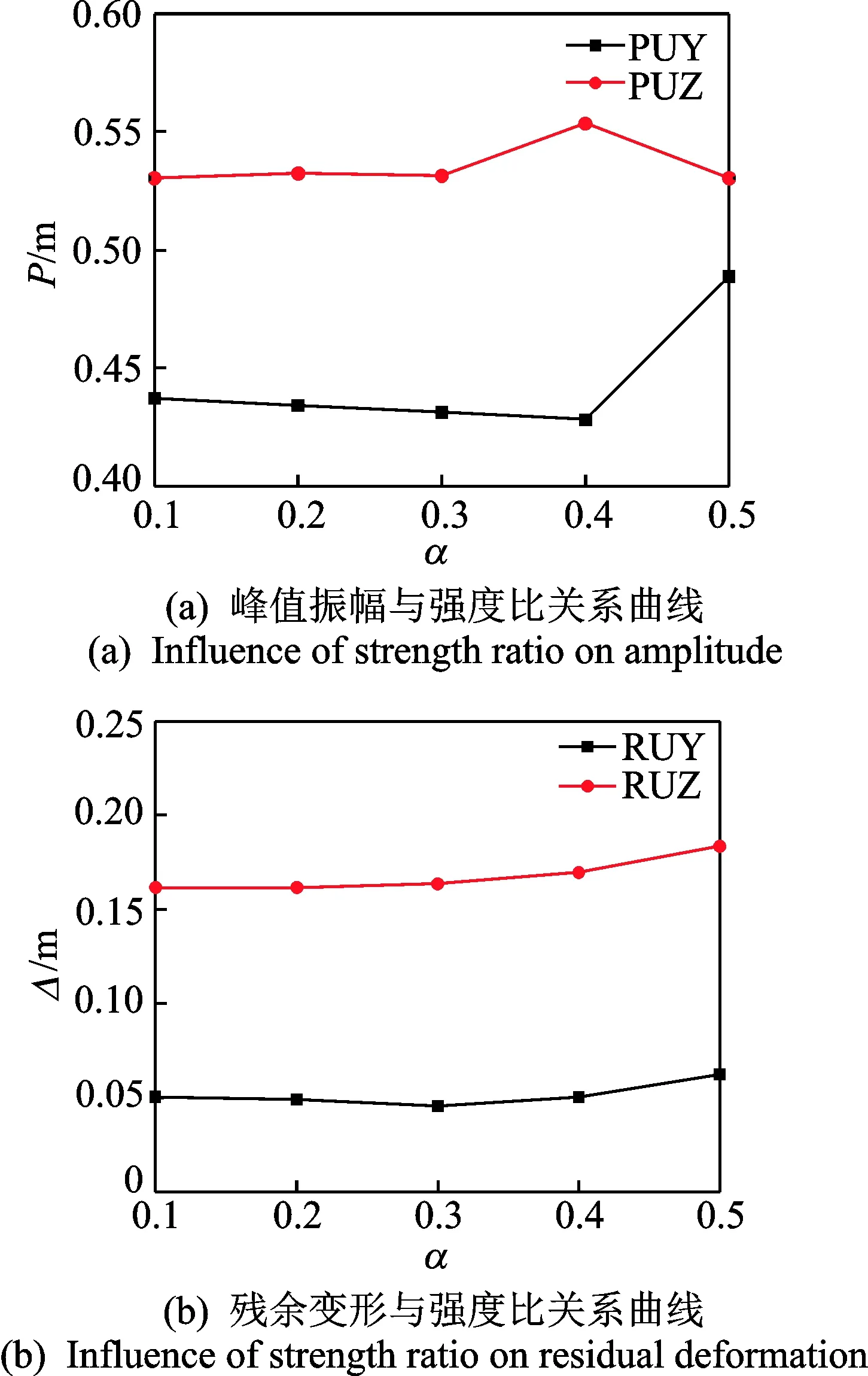
图9 自定心耗能支撑强度比影响曲线Fig.9 Influence curve by different strength ratio of SCEDB
图 10给出了两组不同α值下的自定心耗能支撑滞回曲线比较,可以看出,在保持总启动力不变的情况下,较小的摩擦力设置(α=0.1)使得支撑的滞回面积变小。同时由于保持启动力不变,因此预应力筋截面积增加,支撑第2刚度增加,但此时的支撑具有良好的自复位能力,其自身残余变形很小,可以忽略。当摩擦力设置较大时(α=0.5),其滞回曲线饱满,耗能较多,但是其第2刚度下降,且残余变形增加。因此,α值增大可以提高支撑耗能,但会产生一定的残余变形,并减小结构的自复位能力。
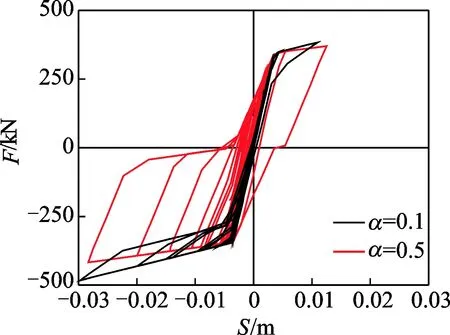
图10 不同强度比下滞回曲线Fig.10 Hysteretic curve with different strength ratio
3.3 启动位移
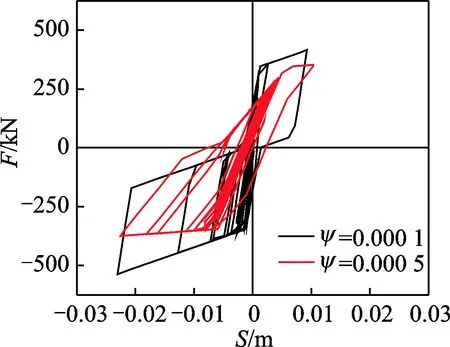
自定心耗能支撑的启动位移Sy对于支撑性能具有较大的影响。通常在多遇地震作用下,支撑处于弹性状态,即支撑位移S 为保证支撑在地震作用下的耗能作用,本研究中控制材料屈服应变ψ<0.000 5,并分析其对于张弦结构跨中峰值振幅以及残余变形的影响,分析结果见图 11和图 12。 图11 自定心耗能支撑屈服应变影响曲线Fig.11 Influence curve by different yield strain of SCEDB 图12 不同屈服应变下滞回曲线Fig.12 Hysteretic curve with different yield strain 图 11(a)给出了结构峰值振幅与屈服应变关系曲线,从图中可以看出,随着屈服应变的增加,水平和竖直方向的振幅出现增加,且竖直方向增幅较为明显。从图 11(b)可以看出,屈服应变对于结构整体残余变形的影响较小。 图 12给出了ψ=0.000 1和ψ=0.000 5时的滞回曲线对比,可以看出屈服应变的增加使得支撑的滞回性能下降,自复位能力降低,同时支撑的残余变形将会增大。 1) 相对于原结构,增加自定心耗能支撑的结构在罕遇地震作用下能够有效地控制结构的残余变形,有利于结构在余震下的抗倒塌及震后的修复工作,但自定心耗能支撑对于结构峰值振幅影响较小。 2) 自定心支撑的启动力、支撑强度比以及支撑启动位移对于结构的振动响应以及抗震性能均有影响。启动力对于支撑结构水平方向的残余变形可以进行有效的控制,调整可使得结构水平方向残余变形接近于零,并能有效降低竖直方向的残余变形,有助于减小结构损伤。同时,支撑强度比对于支撑的耗能以及残余变形有着显著的影响,减小强度比将会减小结构残余变形并提高自复位能力,但同时其耗能将会减小。另外,支撑启动位移的增加会增加结构的峰值位移和支撑残余变形,并降低其耗能能力,同时其对于结构的残余变形影响不显著。因此,在结构抗震设计时,应控制支撑的启动位移。 [1] 周臻,孟少平,吴京. 大跨弦支穹顶结构的振动模态与地震响应分析[J]. 振动、测试与诊断,2013,33(4):609-613. Zhou Zhen, Meng Shaoping, Wu Jing. Vibration modal and earthquake response analysis of large span chord dome[J]. Journal of Vibration,Measurement & Diagnosis, 2013, 33(4): 609-613.(in Chinese) [2] Saitho M, Okada A, Maejima K, et al. Study on mechanical characteristics of light-weight complex structure composed of a membrane and a beam string structure[C]∥Procedings of the IASS-ASCE International Symposium 1994 on Spatial, Lattice and Tension Structures.Atlanta:ASCE, 1994:632-641. [3] 黄明鑫, 钱卫军, 黄开龙,等. 哈尔滨国际会展体育中心大跨张弦桁架结构的安装技术[J]. 工业建筑,2007, 37(9): 41-44. Huang Mingxin, Qian Weijun, Huang Kailong, et al. Erection technology of large span chord-tension truss structure for harbin international exhibition center[J]. Industrial Construction, 2007, 37(9): 41-44. (in Chinese) [4] 孙文波, 杨叔庸, 陈荣毅,等. 广州国际会展中心张弦桁架竖向刚度性能[J].华南理工大学学报:自然科学版, 2003, 31(11): 33-36. Sun Wenbo, Yang Shuyong, Chen Rongyi, et al. Stiffness performance of truss-string structure of guangzhou international convention and exhibition center[J]. Journal of South China University of Technology: Natural Science Edition, 2003, 31(11): 33-36. (in Chinese) [5] 罗尧治, 余佳亮. 北京北站站台大跨度张弦桁架雨棚设计研究[J]. 中国铁道科学, 2013,34(1): 35-42. Luo Yaozhi, Yu Jialiang. Design and research of the long-span truss string structure for the platform canopy of beijing north station[J]. China Railway Science, 2013,34(1): 35-42. (in Chinese) [6] 熊伟, 吴敏哲. 张弦桁架的桁架优化设计[J]. 西安建筑科技大学学报:自然科学版, 2005, 37(2): 215-219. Xiong Wei, Wu Minzhe. Truss optimization design of truss string structure[J]. Journal of Xi′An University of Architecture & Technology: Natural Science Edition, 2005,37(2):215-219. (in Chinese) [7] 朱奕锋, 冯健, 蔡建国, 等. 梅江会展中心张弦桁架抗连续倒塌分析[J]. 建筑结构学报,2013,34(3):45-53. Zhu Yifeng ,Feng Jian ,Cai Jianguo , et al. Analysis on progressive collapse resistance of truss string structure of Meijiang Exhibition Center[J]. Journal of Building Structures, 2013, 34(3): 45-53. (in Chinese) [8] Christopoulos C, Tremblay R, Kim H J, et al. Self-centering energy dissipative bracing system for the seismic resistance of structures: development and validation[J]. Journal of Structural Engineering, 2008, 134(1):96-107. [9] Miller D J, Fahnestock L A, Eatherton M R. Development and experimental validation of a nickel-titanium shape memory alloy self-centering buckling-restrained brace[J]. Engineering Structures, 2012, 40:288-298. [10] 谢钦, 周臻, 孟少平,等. SMA预拉杆式自定心屈曲约束支撑的滞回性能分析[J]. 东南大学学报:自然科学版,2014,44(4):799-804. Xie Qin, Zhou Zhen, Meng Shaoping, et al. Hysteretic performance analysis of self-centering buckling-restrained braces with pretensioned SMA tendons[J]. Journal of Southeast University :Natural Science Edition, 2014, 44(4): 799-804. (in Chinese) [11] Tremblay R, Lacerte M, Christopoulos C. Seismic response of multistory buildings with self-centering energy dissipative steel braces[J]. Journal of Structural Engineering, 2014, 134(1):108-120. [12] Zhou Zhen, He Xianting, Wu Jing,et al. Development of a novel self-centering buckling-restrained braces with BFRP composite tendons[J]. Steel and Composite Structures, 2014, 16(5): 491-506. 10.16450/j.cnki.issn.1004-6801.2017.06.019 国家自然科学基金资助项目(51578558,51208095);中国京冶工程技术有限公司重大课题资助项目(JAF2014KJ01);江苏省“青蓝工程”和江苏省2015年度普通高校研究生实践创新计划共同资助项目(SJLX15_0033) 2016-03-01; 2016-05-03 TU393.3 曾滨,男,1961年1月生,博士。主要研究方向为预应力技术及装备、预应力结构、结构检测鉴定改造加固及新型结构抗震体系。曾发表《新型柔性张拉悬挂体系及其受力性能分析》(《土木工程学报》2010年第43卷增刊)等论文。 E-mail:zengbin@cribc.com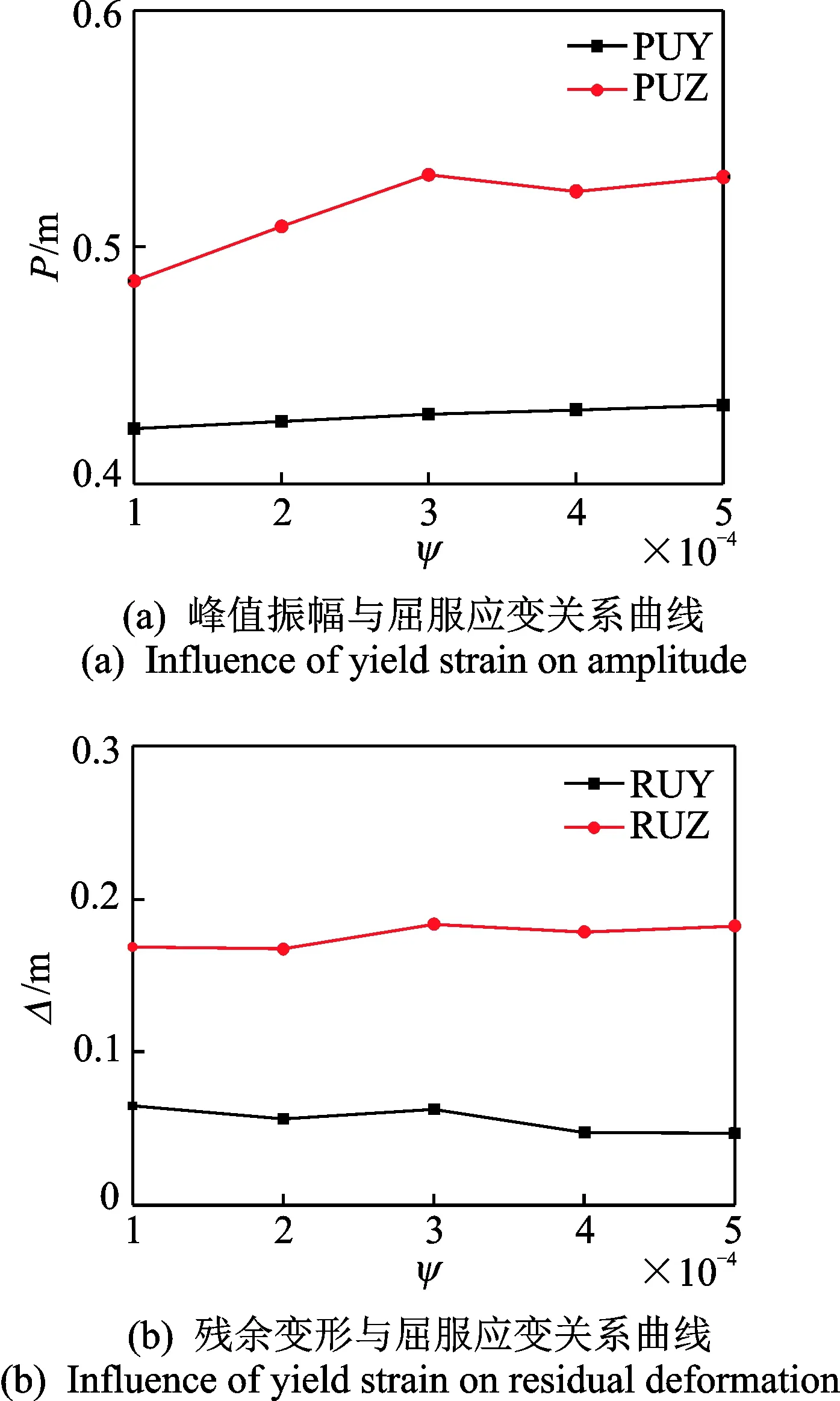
4 结 论

