IEWT和FSK在齿轮与滚动轴承故障诊断中的应用

2018-01-04高雪媛张力佳李媛媛

振动、测试与诊断 2017年6期

关键词：峭度谱分析分量

向玲，高雪媛，张力佳，李媛媛

(华北电力大学(保定)机械工程系保定，071003)

IEWT和FSK在齿轮与滚动轴承故障诊断中的应用

向玲，高雪媛，张力佳，李媛媛

(华北电力大学(保定)机械工程系保定，071003)

改进的经验小波变换方法(improved empirical wavelet transform，简称IEWT)是一种新的自适应性信号处理方法，将这种方法和快速谱峭度(fast spectral kurtosis，简称FSK)相结合，进行齿轮与滚动轴承的故障诊断。首先，采用IEWT对信号进行分解，筛选出故障特征最为明显的2个分量并重构信号；其次，对重构信号进行快速谱峭度滤波；最后，对滤波后的信号进行包络谱分析，提取出信号的故障特征。分析齿轮断齿及滚动轴承故障信号，与直接包络谱和基于EMD经验模态分解(empirical mode decomposition,简称EMD)方法的FSK滤波包络谱分析方法相比可知，采用IEWT处理后再进行FSK滤波的信号进行包络谱分析更具有区分性，可有效识别齿轮和滚动轴承的故障特征。

经验小波分解；快速谱峭度滤波；包络谱分析；故障诊断

引言

齿轮和滚动轴承的故障信号均为非平稳调制信号。共振解调技术[1]是目前最常用的齿轮、轴承故障诊断方法，该方法需要先对信号进行带通滤波，再进行包络谱分析。由于带通滤波器的中心频率选择困难，且对分析结果影响较大，其应用受到了限制。峭度能够敏锐地反映出瞬态冲击成分，可作为选择带通滤波器中心频率的衡量标准，但是峭度无法在强噪声信号中检测到瞬态冲击成分，谱峭度[2-3]可以适应强噪声环境，但其估计值只在平稳状态下是稳定的。Antoni[4]为了解决这些问题提出快速谱峭度滤波方法，通过计算故障信号中每个频段的谱峭度值，可以迅速找到谱峭度值最大时所对应的频率和频率分辨率，以此作为滤波器的中心频率和带宽，虽然在强噪声环境中效果有所改善，结果仍不理想。蒋超等[5]利用EEMD和快速谱峭度，提出了一种敏感IMF选取方法。蔡艳平等[6]提出的方法解决了包络谱分析中主观性给结果带来的影响，但是EMD方法仍存在诸多问题，如过包络、欠包络、模态混叠和端点效应等[7-9]。Gilles[10]提出一种对信号傅里叶频谱进行自适应地划分滤波的信号处理方法，即经验小波变换(empirical wavelet transform,简称EWT)，滤波后可以得到一组单分量，该信号处理方法的计算速度快，模态混叠和端点效应减弱。为了进一步抑制模态混叠效应产生的负面影响，Gilles等[11]提出了EWT方法中窗函数边界线选择的优化方法，但仅将该方法应用于脑电波及地震信号，并未应用到齿轮及轴承故障诊断的研究领域中。在以上研究基础上，笔者提出一种基于IEWT和FSK滤波的诊断方法，将其应用到齿轮与滚动轴承故障实例，并与直接包络谱和基于EMD方法的FSK滤波包络谱分析方法进行对比。

1 改进的EWT

经验小波变换是一种自适应的信号处理方法。首先，规定规范化的信号傅里叶频谱的频率范围为[0,π]，假设将傅里叶频谱分成N个部分，并且以ωn表示相邻两个区域的分界点，共需要确定N+1条分界线，其中0和π分别为第1条和最后一条分界线，那么，还需要确定其余N-1条分界线，以相邻两个连续极大值的中点为分界线所在点[9]。于是，最终得到傅里叶频谱分界点为

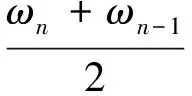
(1≤n≤N-1;ω0=0;ωN=π)

(1)

当傅里叶频谱中的两个分量简单易分时，将两个连续极大值的中点作为分界点十分简单有效，但是当连续的两个分量分别为紧支撑和宽支撑时，该种方法就会失效，导致分界线落在支撑较宽的分量内部，产生模态混叠。Gilles[10]提出了避免该种情况出现的最简单的方法，即找到两个连续极大值之间的极小值，以该点作为两个连续分量的分界线。如果以Ωn表示ωn-1和ωn之间的局部极小值，则

ωn=argminΩn

(1≤n≤N-1;ω0=0;ωN=π)

(2)

图1 分界线示意图Fig.1 Dividing line diagram

对分割区间Λn加小波窗，按照Meyer小波的构造方法，得到经验尺度函数和经验小波函数[10]为

F1,t(ψn)(ω)=

(3)

F1,t(φ1)(ω)=

(4)

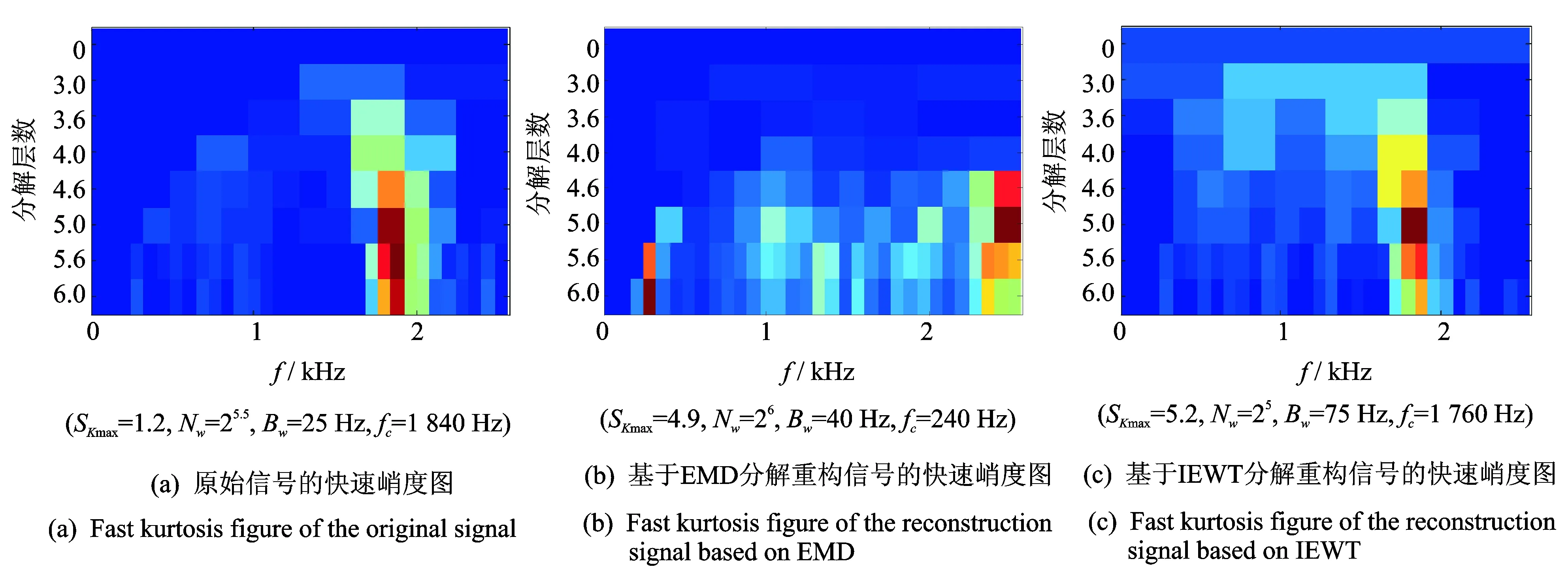
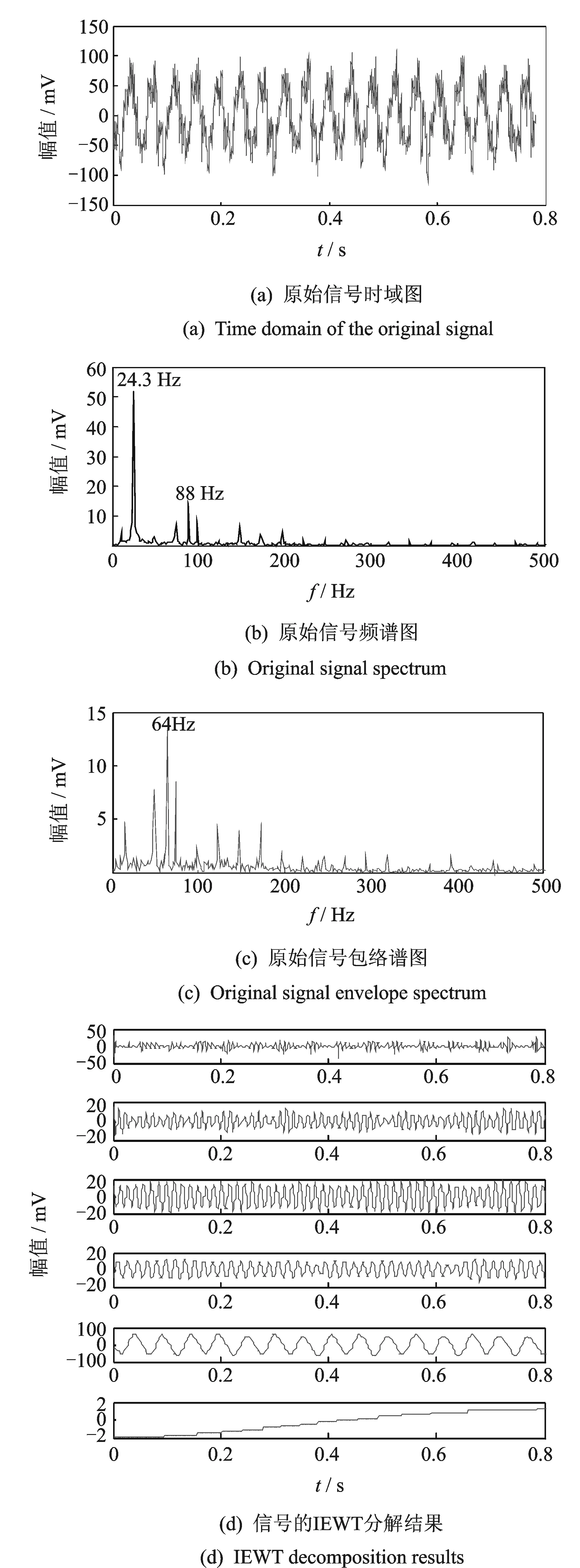
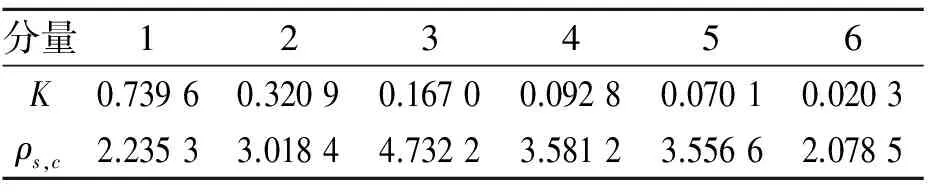
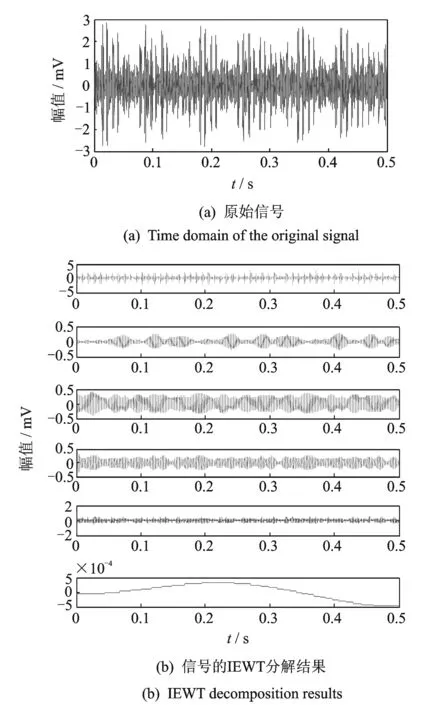
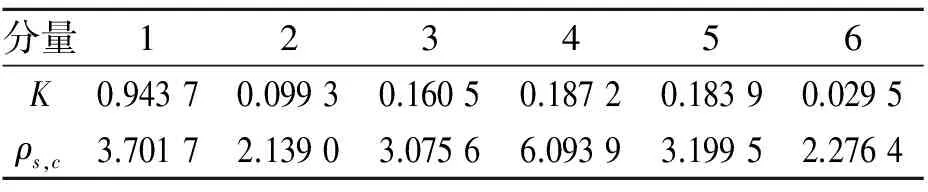
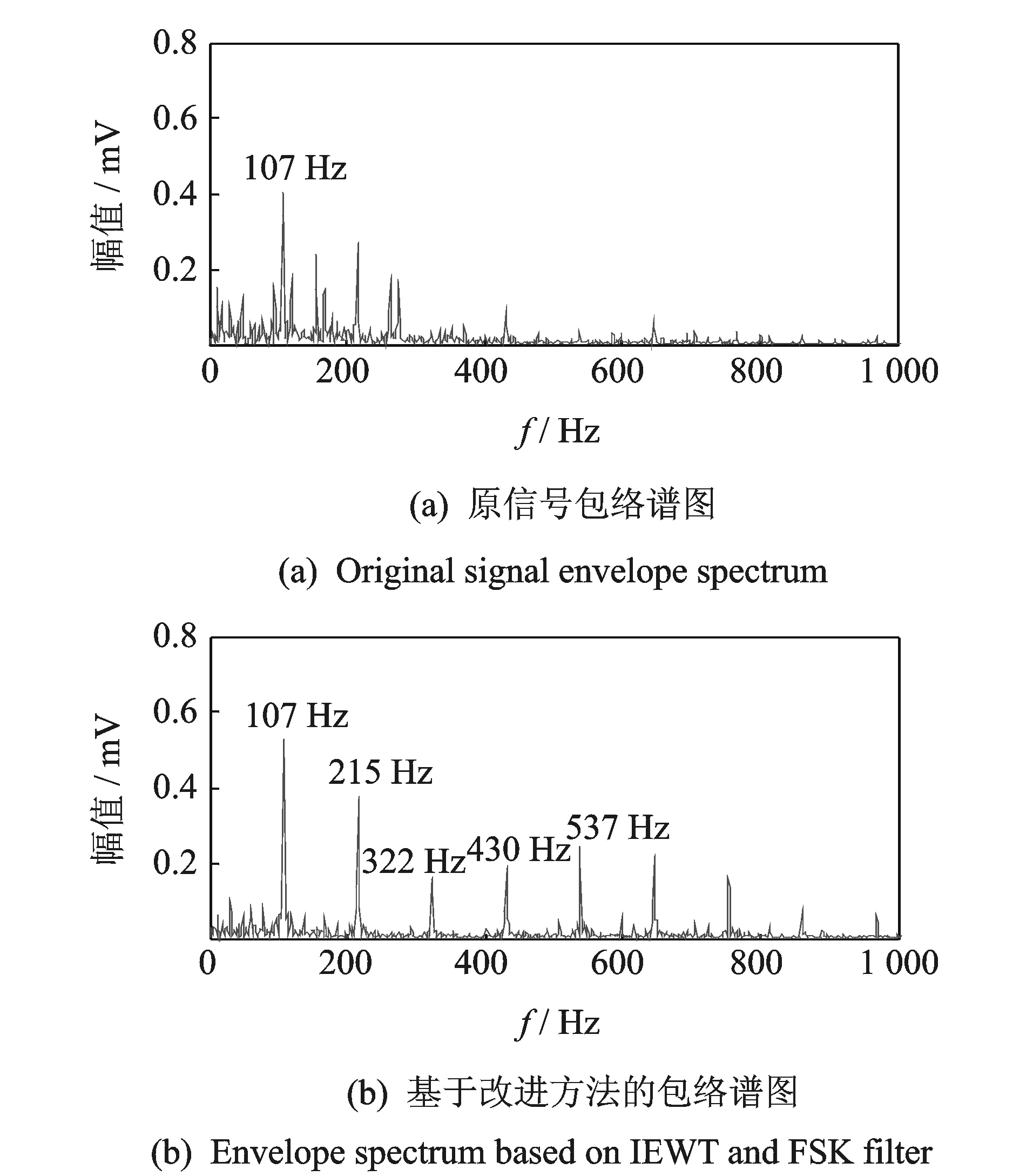
其中：γ

由经验小波函数内积计算得到的细节系数以及由经验尺度函数的内积计算得到的近似系数[11]分别为

(5)

(6)

对信号进行重构，则重构信号[11]可以表示为

(7)

2 快速谱峭度图

对于非平稳信号，如何选择最优频率和频率分辨率是关键问题，为了解决该问题，并达到快速计算谱峭度的目的，文献[12]提出快速峭度图方法。该方法将信号按照每层2n个频段进行分解，然后计算每层每个频段的谱峭度值，谱峭度估计值是频率f和频率分辨率Δf的函数，通过计算时频图上每个频率成分的谱峭度值从而得到谱峭度值最大时对应的f和Δf，即最优带通滤波器中心频率以及带宽，其中Δf≈fs·2/Nω[13]。快速谱峭度图如图2所示，其横坐标为频率值f，纵坐标为分解层数n，图中频段颜色越深代表谱峭度值越大，可以方便确定谱峭度值最大时所对应的f和Δf的最优组合。

图2 断齿故障快速峭度图Fig.2 Fast kurtosis figure of broken teeth failure

3 故障诊断流程

谱峭度法在齿轮和轴承故障诊断应用中获得了一定的成果，但无法适应高噪声环境。胡爱军等[14]提出基于集合经验模态分解(ensemble empirical mode decomposition,简称EEMD)与谱峭度准则的包络谱分析方法，用峭度最大准则选取IMF分量进行包络谱分解，提取出轴承故障的特征信息。苏文胜等[15]提出基于相关系数和谱峭度准则的EMD降噪方法对信号进行预处理，更好地诊断出滚动轴承早期故障。利用上述文献中提出的采用相关系数和谱峭度准则剔除无关分量方法，采用基于互相关系数和峭度准则的IEWT来对信号进行预处理，突出高频共振成分，减少噪声。基于IEWT和FSK滤波的具体诊断流程如下：

1) 对信号进行IEWT分解；

2) 计算分解后各分量的峭度值和相关系数，筛选出相关系数和峭度值最大的分量重构信号；

3) 利用快速谱峭度图方法计算得到带通滤波器的最优中心频率和带宽，然后对滤波后的信号进行包络谱分析，以确定故障特征频率。

4 试验信号诊断方法对比

4.1 齿轮断齿故障

QPZZ-II旋转机械振动故障模拟实验平台如图3所示，可快速模拟旋转机械多种故障状态。齿轮传动比为75∶55。

图3 QPZZ-II模拟实验平台Fig.3 QPZZ-II simulation experiment platform

在输入轴的大齿轮上加工出断齿故障，将加速度传感器安装在齿轮箱箱体上。其中，输入轴转速为1 500 r/min，断齿故障频率与轴的转频相同为25 Hz，采样频率为5 120 Hz。图4给出了原信号的时域图、频域图、包络谱图及经IEWT分解后各分量的时域波形图。

图4 断齿故障信号分析Fig.4 The signal analysis for broken teeth fault

在图4中，断齿故障信号的时域波形虽然有明显的冲击成分，但难以分辨出具体特征；频谱图中能看到旋转频率，但不存在倍频成分等故障特征频率；包络谱图中，频率成分混乱，无法判断齿轮发生何种故障。由式(8)和式(9)计算齿轮断齿故障信号经EMD和IEWT分解后各分量的峭度值和相关系数，结果如表1、表2所示。

峭度值

(8)

4.2 轴承外圈故障

轴承外圈故障信号为凯斯西储大学轴承数据。实验所选用轴承为SKF6205深沟球轴承，布置单点外圈故障，故障直径为0.178 mm。其中，驱动电机转速为1 797 r/min，采样频率设置为12 kHz。轴承节圆直径为39 mm，滚动体直径为7.9 mm，压力角α=0°，由式(10)可计算得到轴承外圈故障频率为107 Hz

(10)

其中：d为滚动体直径；D为轴承的节圆直径；α为接触角；N为滚动体个数；fr为轴的转频。

原信号和经IEWT分解后各分量的时域波形如图6所示。

图6 轴承外圈故障信号分析Fig.6 The signal analysis for outer ring fault of bearing

计算轴承外圈故障信号经IEWT分解后各分量的峭度值和相关系数，结果如表3所示。

表3各分量相关系数K及峭度值ρs,c

Tab.3Thecorrelationcoefficientandkurtosisvalueofeachcomponent

分量123456K0．94370．09930．16050．18720．18390．0295ρs，c3．70172．13903．07566．09393．19952．2764

由表3可知，分量1和分量4的互相关系数及谱峭度值最大，故取这2个分量对信号进行重构。对重构的信号进行快速谱峭度分析，得到如图7所示的快速谱峭度图。

图7 轴承外圈故障快速峭度图Fig.7 Fast kurtosis figure of bearing outer ring fault

由图7可知，重构信号的最大谱峭度值为3.7，谱峭度值最大时所对应的分解层数为3，滤波器中心频率和带宽组合为[750，750]Hz。以该中心频率和带宽构造滤波器，对信号进行滤波，再对滤波后的信号进行包络谱分析，得到如图8所示的原始信号包络谱及基于IEWT和FSK滤波的信号包络谱。

图8 外圈故障信号包络谱图Fig.8 The signal envelope spectrum for outer ring fault

图8(a)为对原始信号直接进行包络谱分析的结果，图中显示故障特征频率107 Hz明显，但故障频率倍频成分的幅值较低，不易分辨。基于IEWT和FSK滤波的包络谱分析结果中，30，107，215，322和430 Hz等频率成分的幅值都比较突出，分别对应故障信号的转频、故障频率及故障频率的2倍频、3倍频及4倍频，故障特征明显，由此可以判断该故障为滚动轴承外圈故障。

5 结束语

提出基于IEWT降噪和快速谱峭度FSK滤波的包络谱分析方法，将IEWT方法代替传统的EMD方法，对信号进行分解重构，克服了EMD方法产生的模态混叠和端点效应，降噪效果更加突出。将该方法应用到断齿齿轮故障和滚动轴承外圈故障的实验模拟数据中，并对IEWT方法和EMD方法的诊断性能进行比较，结果表明，IEWT降噪和FSK滤波的包络谱分析方法得到的包络谱图故障特征更加明显，证明了该方法的有效性。

[1] 王平, 廖明夫. 滚动轴承故障诊断的自适应共振解调技术[J]. 航空动力学报, 2005,20(4):606-612.

Wang Ping, Liao Mingfu. Adaptive demodulated resonance technique for the rolling bearing fault diagnosis[J]. Journal of Aerospace Power, 2005, 20(4):606-612. (in Chinese)

[2] Dwyer R F. Detection of non-Gaussian signals by frequency domen Kurtosis estimation[C]∥Acoustics Speech and Signal Processing, IEEE International Conference on ICASSP.Boston:IEEE, 1983:607-610.

[3] Antoni J, Randall R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines[J]. Systems and Signal Processing, 2006, 20(2):308-331.

[4] Antoni J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 21(1):108-124.

[5] 蒋超, 刘树林, 姜锐红,等. 基于快速谱峭度图的EEMD内禀模态分量选取方法[J]. 振动、测试与诊断, 2015(6):1173-1178.

Jiang Chao, Liu Shulin, Jiang Ruihong, et al. Feature extraction method of intrinsic mode function in EEMD based on fast kurtogram in machinery fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2015(6):1173-1178. (in Chinese)

[6] 蔡艳平, 李艾华, 石林锁, 等. 基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击, 2011, 30(2):167-172,191.

Cai Yanping, Li Aihua, Shi Linsuo, et al. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock, 2011, 30(2): 167-172,191.(in Chinese)

[7] Loh C H, Wu T C, Huang N E. Application of the empirical mode decomposition-Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses[J]. Bulletin of the Seismological Society of America, 2001, 91 (5): 1339-1357.

[8] 孟宗, 顾海燕, 李姗姗. 基于神经网络集成的B样条经验模态分解端点效应抑制方法[J]. 机械工程学报, 2013, 49(9):106-112.

Meng Zong, Gu Haiyan, Li Shanshan. Restraining method for end effect of B-spline empirical mode decomposition based on neural network ensemble[J]. Journal of Mechanical Engineering, 2013,49 (9):106-112. (in Chinese)

[9] 陈浩, 郭军海, 齐巍. 基于经验小波变换的目标加速度估计算法[J]. 北京航空航天大学学报, 2014, 41(1):14-19.

Chen Hao, Guo Junhai, Qi Wei. Estimation of target′s acceleration based on empirical wavelet transform[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 41(1):14-19. (in Chinese)

[10] Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16):3999-4010.

[11] Gilles J, Tran G, Osher S. 2D empirical transforms.wavelets, ridgelets and curvelets revisited[J]. Siam Journal on Imaging Sciences, 2014, 7(7):157-186.

[12] Francis A, Muruganantham C. An adaptive denoising method using empirical wavelet transform[J]. International Journal of Computer Applications, 2015, 117(21):18-20.

[13] 彭畅, 柏林, 谢小亮. 基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J]. 振动与冲击, 2012, 20(31):143-146.

Peng Chang, Bo Lin, Xie Xiaoliang. Fault diagnosis method of rolling element bearings based on EEMD， measure-factor and fast kurtogram[J]. Journal of Vibration and Shock, 2012, 20(31):143-146. (in Chinese)

[14] 胡爱军, 马万里, 唐贵基. 基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J]. 中国电机工程学报, 2012, 32(11):106-111,153.

Hu Aijun, Ma Wanli, Tang Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]. Proceedings of the CSEE, 2012, 32(11):106-111,153. (in Chinese)

[15] 苏文胜, 王奉涛, 张志新,等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击, 2010, 29(3):18-21,201.

Su Wensheng, Wang Fengtao, Zhang Zhixin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock, 2010, 29(3):18-21,201. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.06.028

国家自然科学基金资助项目(51675178,51475164)

2016-01-27；

2016-05-23

TH165.3； TN911.7