渐进成形锥形件壁厚的正弦定理预测精度研究

陈继平 钱健清 王会廷

安徽工业大学冶金工程学院,马鞍山,243032

渐进成形锥形件壁厚的正弦定理预测精度研究

陈继平 钱健清 王会廷

安徽工业大学冶金工程学院,马鞍山,243032

采用不同加工参数渐进成形铝板锥形件，分析渐进成形过程中锥形件的壁厚变化规律，通过比较不同加工条件下实测板料厚度的变化和差异，并与正弦定理的预测值进行对比，研究了正弦定理对渐进成形锥形件壁厚预测的适用范围和精确度。结果表明：渐进成形锥形件过程中板料壁厚的变化经历了壁厚减薄、壁厚回升和壁厚稳定三个阶段，板料在壁厚减薄区和壁厚回升区之间的“最小值点”最易破裂。通过对比实测壁厚与正弦定理理论预测的壁厚发现，在壁厚稳定区的壁厚值最接近正弦定理的理论预测值，正弦定理适用范围在板料的壁厚稳定区。一次加工产生加工硬化，导致二次加工时在接合处的板料难以变形，平均误差率较高。大部分渐进成形锥形件壁厚稳定区实测的板料壁厚比正弦定理的理论预测值略低1%～2%，且进给量对正弦定理精确度的影响较大。此外，采用列文伯格-麦夸特算法和通用全局优化法建立了锥形件壁厚稳定区以及壁厚减薄区和壁厚回升区的壁厚模型经验公式。

渐进成形；铝板；壁厚；锥形件；正弦定理

0 引言

渐进成形是一种通过局部变形的累积产生整体变形的无模成形技术,它以计算机技术为支撑，其中心思想是,将待加工零件的三维数模离散成等高层面的集合，通过CAM软件生成每一层面上的数控加工代码并驱动成形工具逐层成形，最后累积形成所需零件。由于是无模成形，渐进成形不需要专用的模具，而且重复性好，金属的流动能够很好地控制，可以加工出形状复杂的零件。对航天、汽车、家用电器等新产品的开发具有较大的经济价值和广阔的发展前景。

渐进成形技术目前大部分处于实验室研究阶段，研究方法主要为物理实验和数值模拟。很多学者对渐进成形中加工路径的优化[1]、板料的成形性能描述[2-3]、渐进成形数值模拟[4]、提高成形精度[5-6]以及渐进成形的应用[7]等方面进行了深入的研究，但关于板料成形区厚度变化规律的研究不多。周六如[8]认为数控渐进成形中材料厚度变化遵循正弦定律，成形极限和厚度有很大关系。马琳伟等[9]利用数值模拟对板料壁厚进行了研究，并把板料分为4个变形区来考察变形特点。渐进成形中零件的板料壁厚的变化问题目前还没有一个统一的结论，预测壁厚的正弦定理适用范围和精度问题还需要进行深入的研究。

本文旨在揭示渐进成形中锥形件的壁厚变化规律，探索不同条件下板料壁厚的变化情况，通过比较板料厚度的差异，并与正弦定理的预测值进行对比，分析正弦定理的适用范围和精确性，以求增强对渐进成形过程中板料壁厚变化的控制，提高板料的成形极限与成形能力，加工出高质量的钣金零件。

1 实验方案和材料

锥形件形状比较简单，是板料数控渐进成形的典型制件之一，理论上采用数控渐进成形工艺能够实现逐点控制板料的变形，成形出较高质量的锥形件。由于锥形件渐进成形过程比较典型，可以很好地用于研究渐进成形板料壁厚的变化规律，所以本文采用锥形件渐进成形实验，研究不同工具头直径、进给量、成形角度、润滑条件(lubrication condition，LC)和二次成形(secondary forming，SF)条件下渐进成形锥形件的壁厚变化规律和厚度分布。锥形件的渐进成形加工参数如表1所示。残余波峰高度是UG中定义进给量的一种方法。本次实验中，0.005 mm的残余波峰高度约相当于0.48 mm的垂直进给量，其他的按倍数增加。锥形件5和锥形件6在进行二次加工时，锥形件5第一次加工后没有拆卸下机床就进行二次加工，锥形件6第一次加工后从夹具上拆卸下来，重新安装进行二次加工。

表1 锥形件渐进成形加工参数

渐进成形实验用板料为3003铝板，板料厚度为0.735 mm，其为Al-Mn系合金，抗拉强度σb为120～160 MPa，屈服强度σ0.2≥85 MPa。

渐进成形时先将铝板用剪板机裁剪为150 mm×150 mm的矩形板料，利用高精度电化打标机和丝网模板在铝板的一面印制网格，网格直径为2 mm，网格间隙为零，用UG建模圆锥件，再后处理生成刀具轨迹和NC代码，然后将代码拷入NH4050渐进成形数控机床，将印好网格的铝板装夹在渐进成形机床工作台的夹具上对刀后开始加工。

成形结束后网格的畸变采用光学方法进行测量，测量工具为显微镜测量仪。将加工好的锥形件放置于工作台上，透过放大镜观察网格，测量其长轴与短轴的长度。长轴与短轴长度分别记为d1和d2，网格原始直径记为d0，测量结果显示板料周向应变为0，得出d2=d0，根据体积不变定律，计算出成形后板料的厚度。由体积不变定律可知，每一个网格单元变形前后体积不变，即

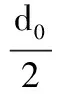
得出

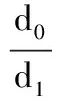
(1)

式中，V0为变形前的网格圆体积；V为变形后的网格圆体积；t0为板料原始厚度；t为板料成形后的厚度。

本次实验选取d0=2 mm，t0=0.735 mm，代入式(1)得t=1.47/d1，测量成形后板料网格圆长轴的长度d1并将其代入式(1)即可计算板料成形后的壁厚t。测量壁厚数据时，壁厚测量点沿圆锥母线从锥口开始编号，相邻测量点间隔为2 mm，距锥口距离s依次记为0，2，4，…，62 mm。

2 实验结果和分析

2.1板料壁厚的正弦定理预测值

MATSUBARA[10]提出了金属板料数控渐进成形技术，对锥形钣金件的渐进成形过程进行了实验研究，认为渐进成形过程金属的变形与旋压成形类似，并且成形后板料的厚度变化与锥形钣金件的半锥角有关，即

t=t0sinθ

(2)

这一研究发现被称为渐进成形正弦定理。根据式(2)得到的板料成形后的壁厚值即为渐进成形正弦定理的壁厚预测值。

2.2板料变形后的壁厚分布

锥形件4与7加工时成形刀具头直径分别为8 mm与6 mm，其他加工参数相同。成形角为35°时，实测壁厚分布与理论预测壁厚关系如图1所示。

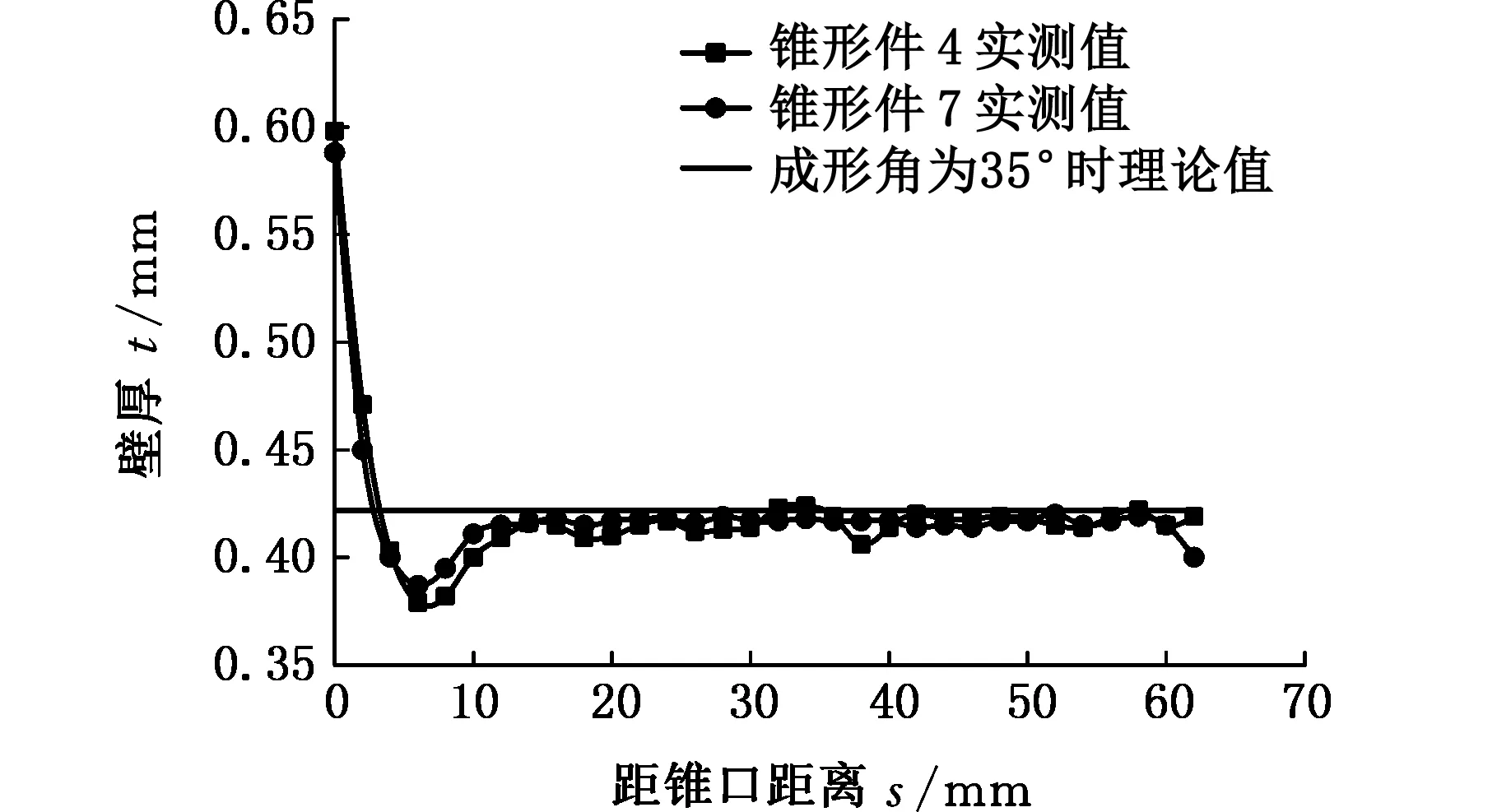
图1 不同工具头直径的锥形件实测壁厚与理论预测壁厚Fig.1 The measured wall thickness and the theoretical predicted values of parts with different tool head diameters

锥形件4在加工时成形工具头与板料之间用机油润滑，锥形件8加工时成形工具头与板料之间无润滑，其他加工参数相同。成形角为35°时，实测壁厚分布与理论预测壁厚关系如图2所示。

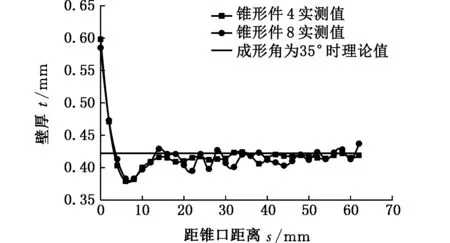
图2 不同润滑条件的锥形件实测壁厚与理论预测壁厚Fig.2 The measured wall thickness and the theoretical predicted values of parts with different lubrication conditions

锥形件1～4加工时进给量分别为残余波峰高度0.100 mm、0.050 mm、0.010 mm、0.005 mm，成形角为35°时，实测壁厚分布与理论预测壁厚关系如图3所示。

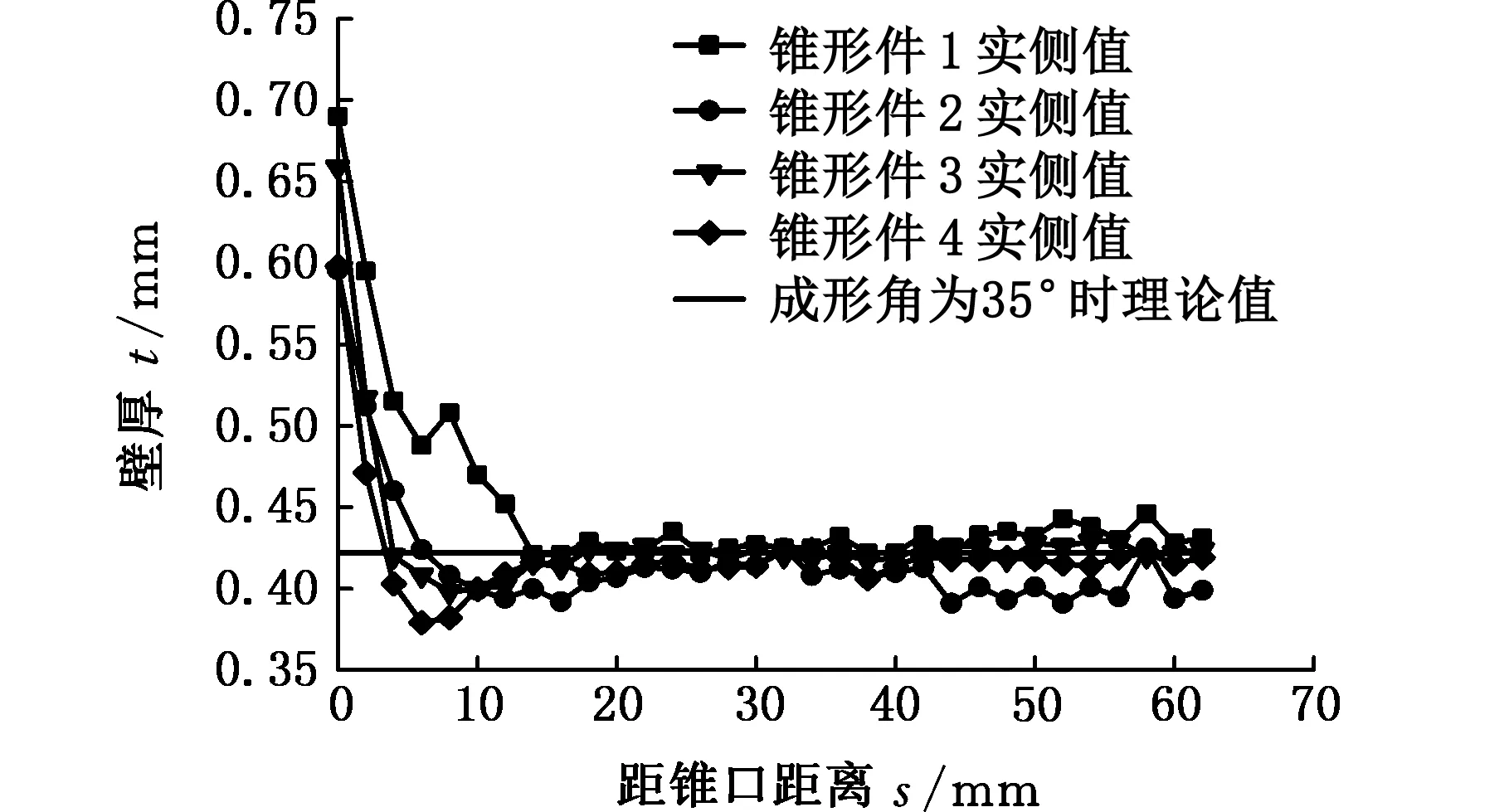
图3 不同进给量的锥形件实测壁厚与理论预测壁厚Fig.3 The measured wall thickness and the theoretical predicted values of parts with different feed amount

锥形件9、4、10的成形角分别为40°、35°、30°(成形角度越小，板料成形后越接近直壁)，其他加工参数相同。实测壁厚分布与理论预测壁厚关系如图4所示。

图4 不同成形角的锥形件实测壁厚与理论预测壁厚Fig.4 The measured wall thickness and the theoretical predicted values of parts with different forming angles

锥形件4、5、6采用的加工方法分别是：一次成形、二次成形(板料不下机床)、二次成形(板料下机床)，其他加工参数相同。二次成形操作步骤为：圆锥件分两次成形，第一次成形深度为30 mm，第二次成形深度为30 mm，其中锥形件5在数控成形机床上不下机床进行二次成形，锥形件6第一次成形后从夹具上卸下，进行网格测量，测量后重新固定在夹具上进行第二次成形，锥形件4为对比件。成形角为35°时，实测壁厚分布和理论预测壁厚关系如图5所示。

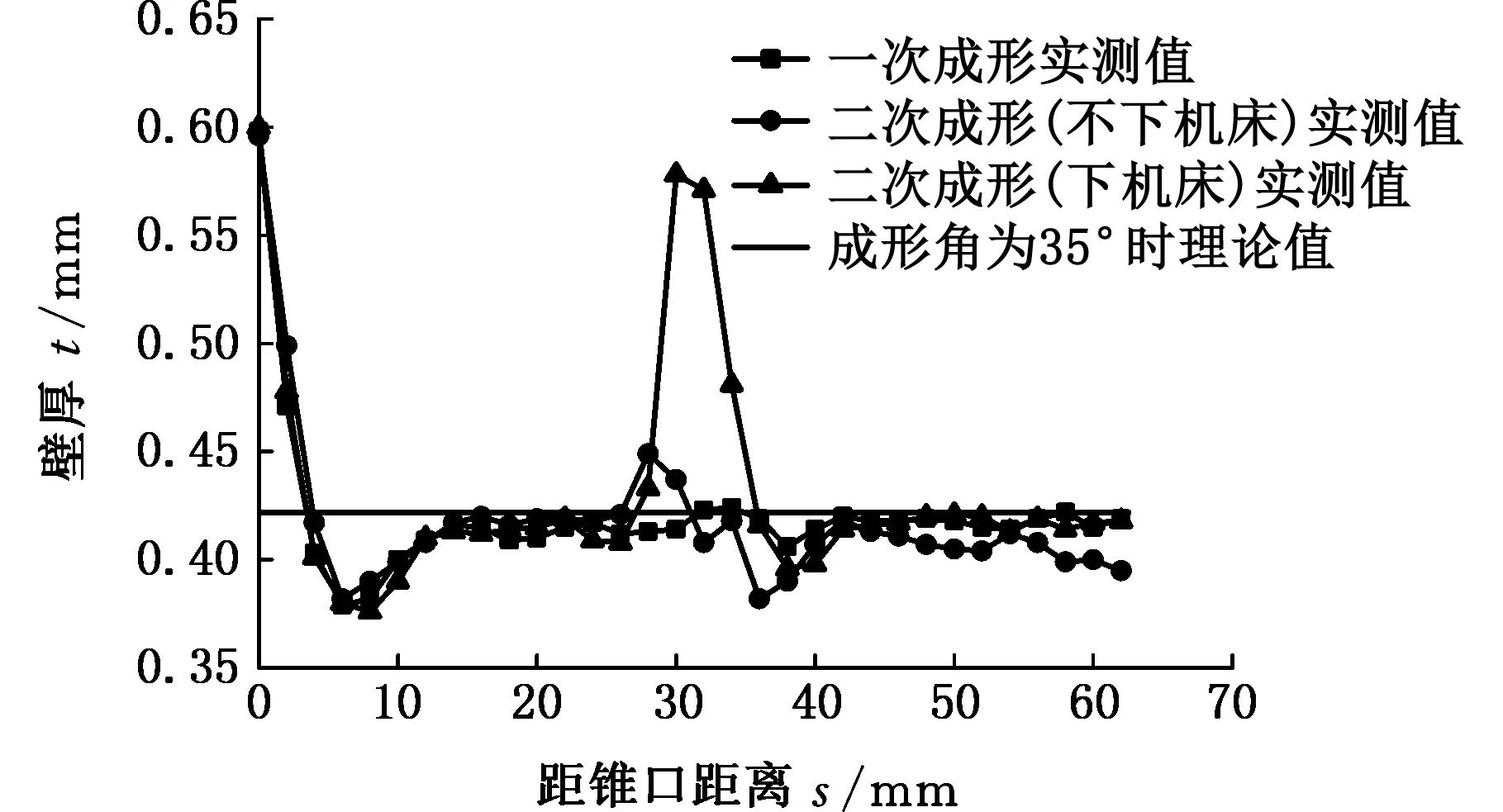
图5 不同二次成形的锥形件实测壁厚与理论预测壁厚Fig.5 The measured wall thickness and the theoretical predicted values of parts with different secondary forming

从上述五种不同的加工参数得到的渐进成形板料壁厚的分布情况可以看出，虽然有些阶段壁厚有差异，但可以从图1～图5中找到板料壁厚分布的共同点：板料壁厚都是从加工边缘起点开始不断减小，到距锥口距离为6 mm左右处板料的厚度同时到达最低点。然后从6 mm一直到14 mm处，壁厚值进入到一个回升的阶段。从14 mm处一直到最后，壁厚值进入到一个稳定的波动阶段，壁厚值都略小于理论预测值。

2.3实验结果的理论分析

在锥形件渐进成形过程中，随着成形角的增大，在制件侧壁上部会出现薄壁区域，该区域在圆周上呈带状分布，称为“减薄带”。在减薄带出现之前制件壁厚与壁厚理论值基本吻合，制件壁厚基本均匀；减薄带出现时，制件壁厚与壁厚理论值在减薄带处相差较大，但制件的其他部分的壁厚值与壁厚理论值仍然基本吻合。

根据上文得到的板料壁厚变化规律，把壁厚发生变形的区域分为三个阶段来进行分析：壁厚减薄区、壁厚回升区和壁厚稳定区(除去了板料压边部位的未变形板料和锥形件的锥尾部分)。把这三个阶段的壁厚变化作为整个渐进成形过程的板料壁厚变化规律来进行研究。

(1)壁厚减薄区。根据上述的实验结果，在不同加工参数和加工条件下，在壁厚减薄区，渐进成形圆锥件壁厚都呈抛物线形逐渐减薄，长度一般为6～7 mm，约占整个板料变形区的十分之一。但是从图3中可以看出，进给量对壁厚减薄区的影响较大，进给量越大，壁厚减薄区持续的长度越长，锥形件1达到了14 mm。这是因为，锥形件杯口边缘距离夹具有一定的距离，存在一段未变形板料，成形时发生弹性变形和弯曲变形，使锥形件杯口边缘的部分很难发生变形。随着进给量的增大，加工层数减少，刀具头在水平方向上的进给量也相应增大，使水平方向上的层与层之间距离增大，弯曲弧长增大，变形不充分，增大了未变形板料区域弹性变形和弯曲变形对板料减薄的影响，使板料减薄速率减小。当进给量相同时，板料原本从水平方向到目标制件的倾斜角度有一个过渡的过程，会发生一定角度的弯曲变形，而板料发生弯曲变形与板料发生纯拉伸变形相比，板料的减薄速率减慢，从图5中可以看出，随着成形角度的增大，弯曲变形的范围增大，壁厚减薄区的长度也同时增大[11]。

(2)壁厚回升区。当板料壁厚减薄区的壁厚值到达最小值之后，板料壁厚会进入一个回升阶段，长度一般为8～10 mm，板料壁厚值一直回升到略小于理论预测值。在壁厚回升区，板料的弹性变形和弯曲变形对壁厚减薄的影响消失，板料变形进入稳定的拉伸变形阶段，壁厚逐渐恢复，直至接近稳定值。

(3)壁厚稳定区。在这个区域，板料壁厚值处在一个稳定的波动阶段，壁厚值最接近正弦定理的理论预测值，一直持续到锥角部分。正弦定理在壁厚稳定区对壁厚的预测具有一定的指导意义。

在壁厚减薄区和壁厚回升区之间的壁厚最小值点(实物图中称为“减薄带”)可以作为判断板料成形时能否破裂以及如何避免破裂的一个参考点。最小值点随着板料尺寸的变化，距离杯口边缘的位置发生变化。总体来说，一般约占板料整体变形部分长度的十分之一。

本文采用五种不同加工参数(成形工具头、摩擦条件、进给量、成形角度和二次加工)成形锥形件来研究渐进成形板料的壁厚变化规律，目的是使得到的壁厚变化规律具有普遍性，不会因为加工参数或者加工条件的改变而变化。

3 关于正弦定理适用范围和精确度的讨论

由式(2)可知，渐进成形锥形件壁厚t只与成形角θ和板料原始壁厚t0有关，而采用正弦定理推导过程中也做了一定的假设：①变形材料是均匀各向同性的；②变形前后的材料不发生体积变化，即满足体积不变定律；③成形工具头与板料之间的摩擦有时可忽略不计；④在成形工具头下的板料瞬间变形时，其他材料不参与变形，即假定是刚性的；⑤在变形过程中，成形工具头、夹具和设备认为是绝对刚性的；⑥板材在渐进成形过程中不发生切向变形，即变形区材料被视为平面变形状态。

在实际板料渐进成形过程中并非完全符合以上假设，存在着复杂的弹塑性变形现象，还有一些不确定因素的影响。因此，正弦定理预测值在实际应用中就存在一些误差，为了提高渐进成形锥形件加工的精度，有必要研究正弦定理对渐进成形锥形件壁厚预测的适用范围和精确度。

3.1正弦定理的适用范围

根据上述渐进成形板料壁厚变化规律可以看出：在板料的整体变形区域中，壁厚减薄区锥形件壁厚t呈抛物线形逐渐减小，正弦定理不适用。壁厚回升区锥形件壁厚t呈抛物线形逐渐增大，正弦定理也不适用。在壁厚稳定区，壁厚值最接近正弦定理理论预测值，虽然有上下波动的情况，但波动幅度都非常小，且分布得比较均匀，所以正弦定理的适用范围在壁厚稳定区。

3.2正弦定理的精确度

通过上述渐进成形板料壁厚在壁厚稳定区的变化规律还可以看出：虽然壁厚稳定区的壁厚值非常接近，但均略小于正弦定理的理论预测值，说明正弦定理的理论预测值和板料的实测壁厚有一定误差。可以把这些误差值ε通过图形方式直观表达出来，形象地说明正弦定理的精确度。锥形件1由于进给量过大，在壁厚最小值点和板料锥尾部分均发生了破裂，排除在外，锥形件2到锥形件10的实测壁厚与理论壁厚的误差柱状图如图6所示。再计算出每个锥形件壁厚稳定区的平均误差率ηε，最后对比可以得出正弦定理的精确度。

用正弦定理的理论壁厚预测值减去每个测量点的实测壁厚值，再除以理论预测值，可以计算出平均误差率(不计正负)。经过计算，锥形件2到锥形件10的实测壁厚与正弦定理的理论预测值的壁厚稳定区的误差率如表2所示。由表2可以看出，锥形件5和锥形件6由于一次加工时产生加工硬化，导致二次加工时在接合处的板料难以变形，所以平均误差率比较高，如图6d和图6e所示。锥形件2由于进给量比较大，平均误差率也比较高。其余锥形件在壁厚稳定区的壁厚平均误差率都比较小，从1%到2%不等。所以可以得出，实测的大部分板料壁厚比正弦定理的理论预测值小1%～2%不等，且进给量对正弦定理精确度的影响较大。

4 渐进成形锥形件的壁厚回归模型

根据3.1节分析结果，正弦定理的适用范围在壁厚稳定区，故对锥形件壁厚稳定区的壁厚数据采用多元非线性模型t=t0sin((ax1+b)(cx2+d)(ex3+f)(gx4+h))进行回归分析。渐进成形锥形件的壁厚减薄区和壁厚回升区的壁厚呈抛物线形逐渐减薄或增厚，对此区段壁厚数据采用多元非线性模型t=t0(ax1+b)(cx2+d)(ex3+f)4sin(gx4+h)进行回归分析。其中t0=0.735 mm，自变量x1表示工具头直径，x2表示进给量，x3表示距锥形件锥口距离，x4表示成形角。

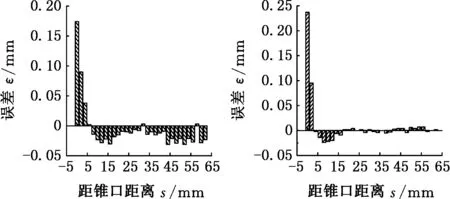
(a)锥形件2 (b)锥形件3

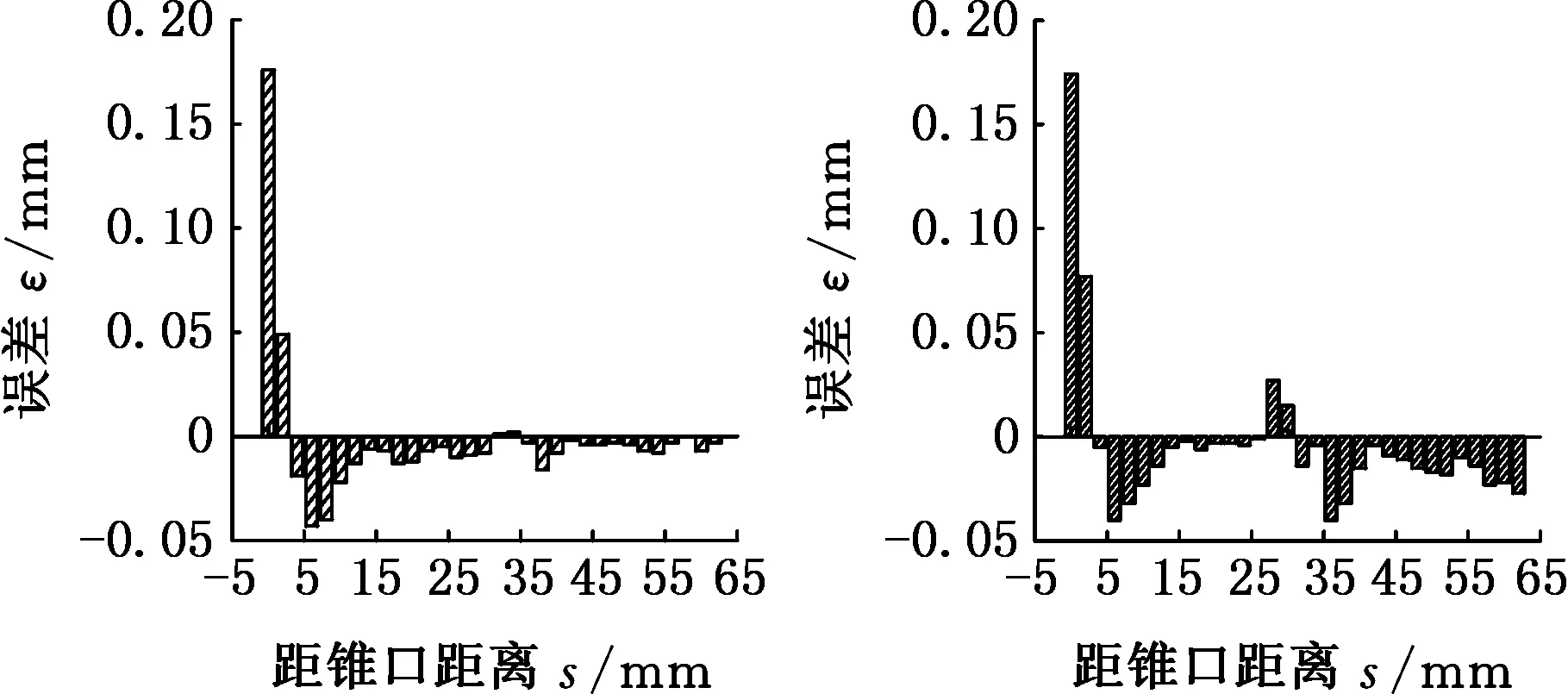
(c)锥形件4 (d)锥形件5

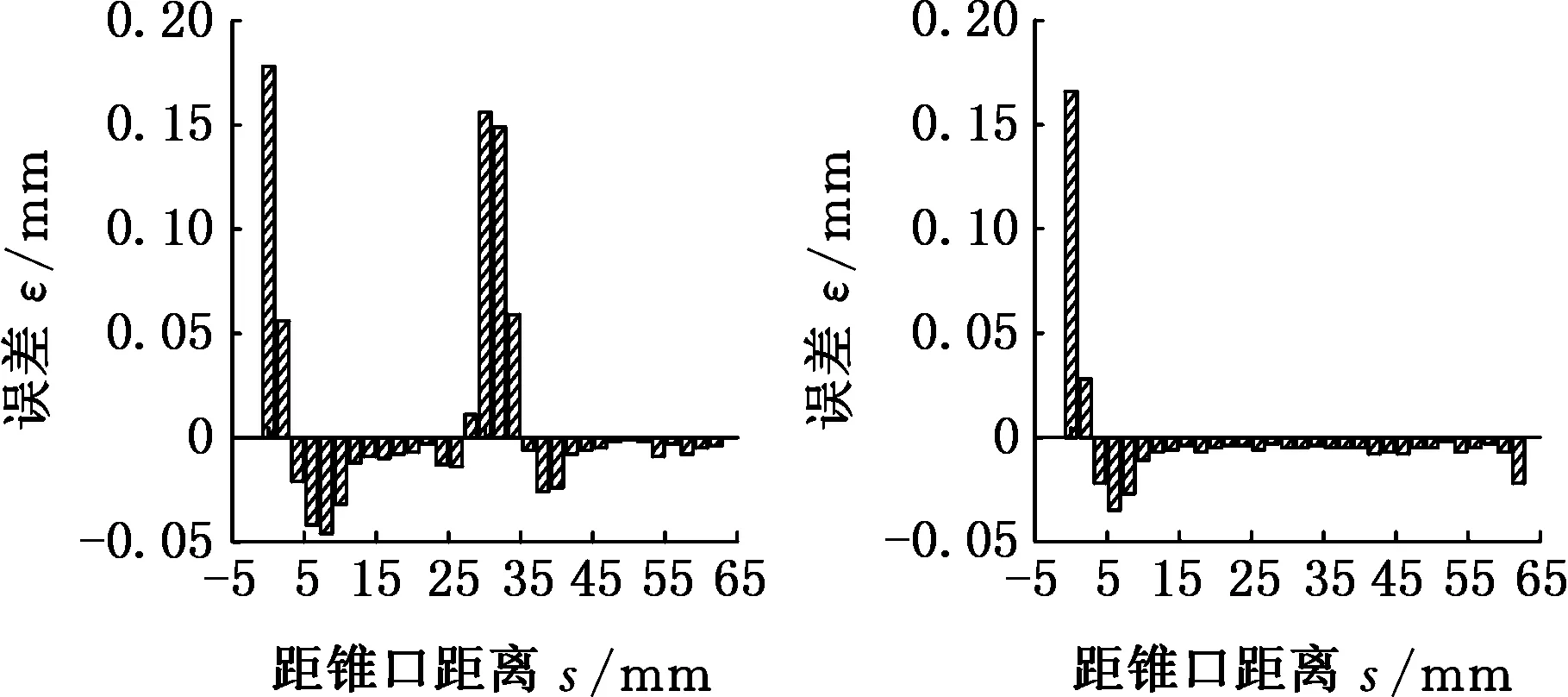
(e)锥形件6 (f)锥形件7

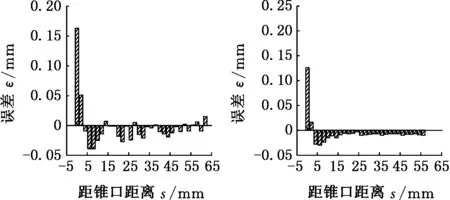
(g)锥形件8 (h)锥形件9

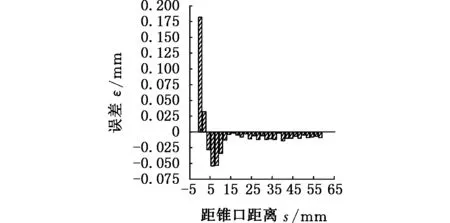
(i)锥形件10图6 实测壁厚与理论预测壁厚的误差Fig.6 The errors between the measured wall thickness and the theoretical predicted values

对锥形件壁厚稳定区的壁厚采用列文伯格-麦夸特算法和通用全局优化法[12]进行回归分析，得到系数a=-12.988 29，b=66.108 87，c=-0.015 62，d=1.105 71，e=-3.587 62，f=1.716 96，g=0.034 82，h=-1.051 64，故壁厚稳定区的壁厚模型经验公式为t=0.735sin((-12.988 29x1+66.108 87)(-0.015 62x2+1.105 71)(-3.587 62x3+1.716 96)(0.034 82x4-1.051 64))，模型的复相关系数R=0.9455，说明锥形件壁厚稳定区的壁厚回归模型的线性相关性高度显著，因此，可以采用此模型对渐进成形锥形件壁厚稳定区的壁厚进行定量分析计算。同理，通过壁厚减薄区和壁厚回升区的模型对锥形件壁厚减薄区和壁厚回升区的壁厚采用列文伯格-麦夸特算法和通用全局优化法进行回归分析，得到系数a=-0.084 39、b=-3.289 97、c=3.388 72、d=1.479 75、e=-0.005 56、f=0.599 91、g=-0.066 89、h=1.073 32，故锥形件壁厚减薄区和壁厚回升区的壁厚模型为t=0.735(-0.084 39·x1-3.289 97)(3.388 72x2+1.479 75)(-0.005 56·x3+0.599 91)4sin(-0.066 89x4+1.073 32)，模型的复相关系数R=0.8767，说明锥形件壁厚减薄区和壁厚回升区的壁厚回归模型高度线性相关，可以采用此模型对渐进成形锥形件壁厚减薄区和壁厚回升区两个强烈非线性变形区域的壁厚进行定量分析计算。上述壁厚回归模型为渐进成形锥形件的壁厚理论预测和实际锥形件渐进成形加工参数的确定和优化提供了较为重要的参考。

5 结论

渐进成形板料壁厚的变化经历了壁厚减薄区、壁厚回升区和壁厚稳定区；锥形件板料在壁厚减薄区和壁厚回升区之间的“最小值点”最易破裂；在壁厚稳定区，壁厚值最接近正弦定理理论预测值，虽然有上下波动的情况，但波动幅度都非常小，且分布得比较均匀，所以正弦定理的适用范围在壁厚稳定区。渐进成形正弦定理的适用范围在板料的壁厚稳定区；一次加工产生加工硬化，导致二次加工时在接合处的板料难以变形，平均误差率较高。大部分渐进成形锥形件壁厚稳定区的实测板料壁厚比正弦定理的理论预测值略小1%～2%，且进给量对正弦定理精确度的影响较大。为了获得渐进成形锥形件的壁厚理论模型，主要考虑工具头直径、进给量、成形角和距锥形件锥口距离等因素的影响，通过锥形件相关变形区域的壁厚回归模型采用列文伯格-麦夸特算法和通用全局优化法获得了锥形件壁厚稳定区以及壁厚减薄区和壁厚回升区的壁厚模型经验公式。

[1] 莫健华，丁勇，黄树槐.金属板材数控单点渐进成形加工轨迹优化研究[J]．中国机械工程，2003，14(24)：2138-2140.

MO Jianhua, DING Yong, HUANG Shuhuai. Research on Tool-path Optimization of Sheet Metal Numerical Control Single Point Incremental Forming[J].China Mechanical Engineering, 2003,14(24):2138-2140.

[2] 肖士昌，高锦张，贾俐俐，等.单道次渐进成形锥形件壁厚均匀临界成形角的研究[J].锻压技术，2012，37(1)：49-54.

XIAO Shichang, GAO Jinzhang, JIA Lili, et al. Research on Critical Forming Angle of Uniform Thickness in Single-path Incremental Forming for Conical Part[J]. Forging amp; Stamping Technology,2012,37(1): 49-54.

[3] YAMASHITA M, GOTOH M, ATSUMI S Y. Numerical Simulation of Incremental Forming of Sheet Metal[J].Journal of Materials Processing Technology,2008,199:163-172.

[4] 李磊，周晚林，刘丹成，等.金属板料单点无模渐进成形数值模拟及分析[J].南京航天航空大学学报，2009，41(5)：611-614.

LI Lei, ZHOU Wanlin, LIU Dancheng, et al. Numerical Simulation and Analysis of Sheet Metal Single-point Dieless Incremental Forming[J].Journal of Nanjing University of Aeronautics amp; Astronautics, 2009, 41(5): 611-614.

[5] AMBROGIO G, FILICE L, NAPOLI L D. A Simple Approach for Reducing Profile Diverting in a Single Point Incremental Forming Process[J]. Part B: Journal of Engineering Manufacture, 2005,219:823-830.

[6] 韦红余，胡铭明，高霖，等.圆锥形渐进成形制件成形精度研究[J].机械工程学报，2010，46(9)：193-198.

WEI Hongyu, HU Mingming, GAO Lin，et al.Investigation on Forming Accuracy of Cone Type Sheet Metal Incremental Forming Parts[J].Journal of Mechanical Engineering, 2010, 46(9):193-198.

[7] AMBROGIO G, NAPOLI L D, FILICE L. Application of Incremental Forming Process for High Customised Medical Product Manufacturing[J]. Journal of Materials Processing Technology, 2005, 162/163:156-162.

[8] 周六如.板料数控渐进成形变形区厚度变化规律的研究[J].机械工程学报，2011，47 (18)：40-50.

ZHOU Liuru.Research on the Thickness Change Laws in Numerical Control Incremental Sheet Forming[J].Journal of Mechanical Engineering, 2011,47(18):40- 50.

[9] 马琳伟，莫建华.基于有限元仿真的金属板材单点渐进成形分析[J].塑性工程学报，2007，14(6)：96-100.

MA Linwei, MO Jianhua. The Mechanical Analysis of Sheet Metal Incremental Formingby Numerical Simulation Based on Solid Element[J].Journal of Plasticity Engineering, 2007, 14(6): 96-100.

[10] MATSUBARA S. A Computer Numerically Controlled Dieless Incremental Forming of a Sheet Metal[J].Proceedings of the Institution of Mechanical Engineers B, Journal of Engineering Manufacture, 2001, 215:959-966.

[11] ALLWOOD J M, SHOULER D R, TEKKAYA A E. The Increased Forming Limits of Incremental Sheet Forming Processes[J]. Journal of Materials Processing Technology, 2007, 344:621-628.

[12] LAN Shuhuai, LEE Heyjin, LEE Soohun, et al. Experimental and Numerical Study on the Viscoelastic Property of Polycarbonate Near Glass Transition Temperature for Micro Thermal Imprint Process[J]. Materials and Design, 2009, 30(9): 3879-3884.

(编辑王艳丽)

StudyonWallThicknessPredictionAccuracybySineLawforIncrementallyFormedConicalParts

CHEN Jiping QIAN Jianqing WANG Huiting

School of Metallurgical Engineering,Anhui University of Technology,Ma’anshan,Anhui,243032

The wall thickness variations of aluminium conical parts were analyzed during incremental forming with different processing parameters. The application scope and accuracy of wall thickness variation by the sine law for incrementally formed aluminium conical parts was studied through comparing the variations and differences of measured wall thicknesses for different processing parameters with the values predicted by the sine law. The results show that the wall thickness variations of conical parts during incremental forming have three stages, i.e. wall thickness thinning stage, wall thickness pick-up stage and wall thickness stable stage. The extremely easy rupture points of sheet metal are “the minimum value points” between the thinning regions and pick-up areas. Through comparing the measured and the predicted wall thickness values, it is found that the wall thickness measured in the stable region is close mostly to the predicted wall thickness values of sine law. The application scopes of wall thickness variation sine law for incrementally formed aluminium conical parts are in the stable regions. Work hardening produced in the primary processing may result in difficult deformations at joints of the sheet metals in secondary processing with higher average error rates. Most measured wall thicknesses in the stable regions for incrementally formed conical parts are 1%～2% lower than the predicted values of sine law. The feed amounts have greater influences on the accuracy of sine law. Furthermore, the wall thickness empirical equations of the wall thickness thinning region, pick-up area and stable region for conical parts were established through Levenberg-Marquardt algorithm and global optimization calculating methods.

incremental forming; aluminum sheet; wall thickness; conical part; sine law

TG386

10.3969/j.issn.1004-132X.2017.22.017

2017-01-03

国家自然科学基金资助项目(51275003)；安徽省自然科学基金资助项目(1508085ME78)

陈继平，男，1975年生。安徽工业大学冶金工程学院副教授。研究方向为渐进成形技术。发表论文30余篇。E-mail: leavejames9443@163.com。钱健清(通信作者)，男，1963年生。安徽工业大学冶金工程学院教授。王会廷，男，1974年生。安徽工业大学冶金工程学院副教授、博士。