基于改进分散搜索算法的多资源跨单元调度问题研究

范佳静 曹玉华 曹 敏

1.浙江科技学院经济与管理学院，杭州，3100232.浙江科技学院机械与汽车工程学院，杭州，310023

基于改进分散搜索算法的多资源跨单元调度问题研究

范佳静1曹玉华1曹 敏2

1.浙江科技学院经济与管理学院，杭州，3100232.浙江科技学院机械与汽车工程学院，杭州，310023

针对单元制造系统中不同设备、操作人员和自动导引小车的特点以及对制造系统的作用，提出了多资源约束下的跨单元调度问题。以零件延期交货、员工工作人数及跨单元移动次数、自动导引小车数量最少为目标，构建目标规划模型。针对模型的特殊性，提出了改进分散搜索算法，算法中应用遗传算法获得新解，应用模式搜索法改进新解，进一步提高了算法的收敛速度。最后将此模型及算法应用于不同规模的8个算例，证明了模型和算法的有效性，针对算例进行详细分析，说明设备、人员和自动导引小车在调度过程中的相互作用。

跨单元；调度；多资源；改进分散搜索算法

0 引言

单元制造(cellular manufacturing，CM)既能结合工作车间方式的灵活性和流水线方式的高效率，又能以近似刚性流水线的成本来生产多品种小批量商品，满足市场在时间、质量、成本、柔性等多方面的要求，代表着生产方式的新方向。单元制造主要包括单元构建、单元设计和单元调度，三方面既相互独立又交互影响[1]。单元调度是实现企业资源优化配置、提高准时交货率的关键因素。在现代制造企业中，多技能员工技术能力的提高、全自动化设备的广泛应用以及AGV小车等自动运输工具的推广使得制造单元间的关系变得更加复杂和紧密，特别是跨单元调度问题中如果仅涉及设备单元调度，而忽略其他要素对生产进度的影响，将导致整个调度方案在实施过程中与计划产生较大偏差，出现延期交货等问题，因此，需对制造单元进行多资源跨单元调度，从而满足调度系统多方面的要求。

目前学者已从不同角度对单元调度问题进行了研究。王跃岗等[2]研究了一类带有时间窗口的自动化制造单元调度问题，即工件在工作站上的加工时间必须在给定的上下限时间范围内，并采用混合量子算法求解调度模型。韩文民等[3]提出在单元制造中，零件可以被分为不同批量，并采用不同的加工方式，从而提高设备效率。在单元调度问题中，部分零件不仅需要在所属单元内的设备上加工，还可能需要跨单元操作，相对于被忽略的单元内物料之间的移动时间，单元间的物料移动时间则必须加以考虑，由此产生了跨单元调度问题。KARTHIKEYAN等[4]在单元构建的基础上提出采用启发式方法进行跨单元调度研究。李冬妮等[5]针对单元制造系统中需要多个单元协作完成的特殊件，提出柔性路径下跨作业单元的特殊工件调度方法——基于信息素的方法 (pheromone-based approach，PBA)，并建立了Agent模型。贾凌云等[6]在文献[5]的基础上，提出了运输能力有限条件下的跨单元调度模型，并采用混合蛙跳和遗传算法求解模型。SOLIMANPUR等[7]以流程时间为标准，结合单元间物料移动时间约束构建了跨单元调度模型，并提出了模型求解的禁忌搜索算法。季少梅[8]、MENG等[9]、PAJOUTAN等[10]均考虑了跨单元调度问题。目前随着AGV小车在单元制造系统中的广泛应用，不少学者针对AGV小车调度问题进行了相关研究。马帅[11]针对带AGV约束的作业车间调度问题工程实例，提出了双系统优化算法与混合编码方式，对约束车间作业问题进行了优化调度。刘旭等[12]解决了混流作业车间中物料配送多自动导引车的调度优化问题，以AGV配送物料行驶时间最短为目标建立数学优化模型，并提出改进遗传算法进行AGV任务分配和配送路径优化。NISHI等[13]针对制造系统中多AGV 路径规划问题，建立了多AGV调度模型，提出分解算法进行求解。从目前AGV小车的调度来看，更多的是将其作为单一资源进行研究，没有同时考虑它对设备调度的影响，有时AGV小车的就近任务分配会导致一些设备上已加工完零件的等待，造成设备堵塞，从而延长整个加工周期，因此需要将AGV小车任务分配与设备调度统一规划。

单元制造系统是一个复杂系统，除机器设备外，人力资源对系统柔性、高效的运行也起着重要作用，随着设备操作技术水平的不段提升，人与设备技术的融合问题显得尤为突出。人们针对双资源单元调度问题进行了研究，如FAN等[14]不仅考虑了人员对单元调度的影响，同时还在制造单元构建和调度中引入了员工学习能力因素，使得模型更加符合实际生产需求。但是在跨单元调度问题中涉及人员调度的研究相对较少。由于多技能员工可以操作不同单元的不同设备，故不仅需要考虑物料在单元间的移动，还需考虑操作人员在单元间的移动。零件的加工顺序和工人工作内容的安排具有很强的关联性，为了缩短零件加工周期，调度方案可能会要求部分技能水平高的人员操作较多的设备，而增加了员工在单元间来回走动的次数；也有可能会为了避免员工在单元间的走动时间，而调整不同零件的加工顺序，在不延期交货的情况下，略微增加零件的整个流程时间。这就需要研究者在跨单元调度中不仅考虑零件在单元间的移动，同时要关注员工的任务分配以及员工的跨单元操作的情况。

本文在多资源跨单元调度问题中同时分析设备、人员和AGV小车等多个资源对零件跨单元操作的影响，进行合理的多资源任务分配，从而获得整体效果的最优，同时也对拓展单元调度问题的内涵和研究方向提供一定的借鉴作用。

1 问题的描述及数学模型的构建

本文提出的多资源约束下的跨单元调度问题认为制造系统中包括K个单元，M台设备(包括一定量的半自动设备和全自动设备，其中全自动设备不需要员工进行配合操作)及需要加工的P种零件，根据零件加工工艺顺序以及设备单元归属情况，零件需要依靠制造系统中的J辆AGV小车实现单元间移动并进行跨单元操作，同时结合无储存条件，当物料被送至指定设备时，如设备上仍有零件在加工，则物料需暂存在AGV小车上，直到设备上的零件加工完为止。在单元制造系统中共有H个多技能员工加工制造系统中的半自动设备，不同员工的技能水平不同，不同员工操作相同设备上的同种零件所需时间不同，为了节约人力资源成本，允许员工操作不同单元内的不同设备。

1.1模型假设及变量设定

为了简化模型的复杂程度，本文提出的目标规划模型基于以下假设：①系统最初所有的设备、AGV小车和员工都处于等待工作状态；②零件只能按一条加工路线进行加工，且加工顺序为已知；③零件在设备上加工的时间、零件设备单元划分、零件的交货时间等基本信息是已知的；④每台设备和AGV小车加工或运输工件都是非中断非抢占式的；⑤每种设备均只有一台，但是AGV小车有若干台；⑥员工操作设备的基本信息为已知；⑦零件需要在不同单元操作时，需考虑零件的搬运时间，但单元内的搬运时间忽略不计；⑧需要考虑操作人员在单元间的走动时间，但单元内的走动时间忽略不计；⑨零件在半自动设备上操作需要员工的辅助配合；⑩不考虑设备的故障问题。

1.2数学模型

1.2.1目标函数分析

结合调度问题的一般要求以及多资源调度问题的特点，本文问题包含四部分目标。

第一部分为调度的基本目标，总延期时间最小，即

(1)

式中，w1为第一个目标函数;Fp为零件p的完工时间；Dp为零件p的交货时间；P为零件总数。

第二部分为人员目标，所需的加工人员最少，即

(2)

式中，w2为第二个目标函数;H为目前员工总数;zh表示第h个员工是否有生产任务，zh=1表示员工h有生产任务，否则zh=0。

加工人员越少，则企业投入的成本越小。

第三部分同为人员目标，员工在单元间移动次数最少，即

(3)

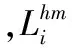
从人的因素考虑，员工在单元间移动次数越少，对跨单元调度的影响就越小，员工的劳动强度也随之下降。

第四部分为AGV小车的使用量最小，即

(4)

式中，w4为第四个目标函数;sj为AGV小车j是否有运输任务，sj=1表示AGV小车j有生产任务，否则sj=0;J为AGV小车的总数。

1.2.2约束条件分析

结合调度一般约束及多资源调度的特点，本文从以下5个方面设定相应的约束条件。

(1)选择约束(操作人员及运输设备的选择约束)。任何零件的任何工序都必须选择一个人来进行操作，对于全自动设备而言，不需要员工的辅助操作，在此虽然安排了人员操作，但是其操作时间为0，故对员工的调度没有任何影响，因此有

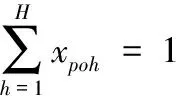
(5)

如果某个零件前后所需设备不在同一单元，则必须选择一台AGV小车对该零件进行单元间的移动，因此有

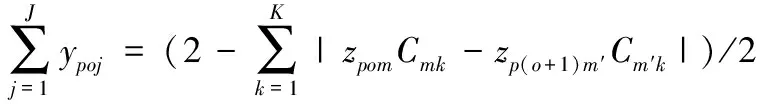
(6)

∀p,o=1,2,…,Op-1

式中，xpoh、ypoj、zpom均为0-1变量，xpoh=1表示零件p的工序o由工人h操作，否则为0；ypoj=1表示零件p的工序o完成后由AGV小车j来进行单元间的运输，否则为0；zpom=1表示零件p的工序o需要在设备m上加工，否则为0；Op为零件p的工序数。

(2)操作时间的约束(零件不同时间的确定)员工开始操作具体零件工序的时间

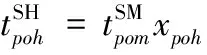
(7)

零件某道工序结束的时间

(8)

∀p，o，m

零件所有工序加工完成的时间

(9)

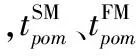
(3)操作顺序约束(零件前后工序操作及运输顺序的约束)。零件后一道工序开始加工的时间必须大于等于前一道工序开始加工的时间与设备加工时间、员工加工时间以及零件移动时间之和,因此有

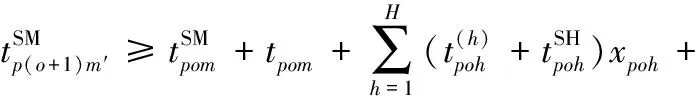
(10)

∀p,o,m,m′

如果零件的某道工序结束后需要应用AGV小车运输，则其开始运输的时间必须大于等于该零件的该道工序结束时间才能进行，因此有

(11)

∀p,o,m,m′,j

当AGV小车将零件运至指定设备后，需要该设备上前一零件加工完才算运输结束，此约束考虑设备堵塞对AGV小车运输的影响，因此有

(12)

∀p,o,p′,o′,m,j

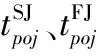
(4)能力约束(设备、人员及AGV小车的能力约束)。在同一时间任何一台设备、人员和AGV小车只能操作或运输一个零件，因此有

(13)

∀p,o,p′,o′,m

(14)

∀p,o,p′,o′,m

(15)

∀p,o,p′,o′,j

式中，ypop′o′h=1表示员工h先操作零件p的工序o，再操作p′的工序o′，否则为0；zpop′o′j=1表示AGV小车j在零件p的工序o操作完后先运输零件p，然后在p′的工序o′操作完后运输零件p′，否则为0；tHT为人员在单元间的移动时间；B为无穷大的数。

(5)变量的逻辑及取值约束如下：

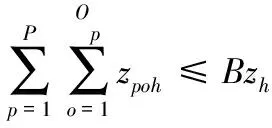
(16)

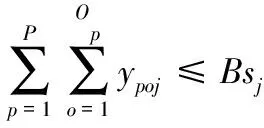
(17)

1.2.3目标规划模型

在企业实际调度中，有时并不需要所有目标达到最优效果，而是根据实际能力来确定具体的要求，故上述模型可以转化为目标规划模型，假设零件超期交货的总时间不得超过G1，员工人数不得超过G2，员工在单元间的移动次数不得超过G3，AGV小车数量不得超过G4，则上述的目标函数可以转化为目标约束：

(18)

(19)

(20)

(21)

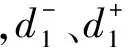
在上述目标中，第一部分与零件的生产时间有关；第二部分和第三部分与员工有关；第四部分与AGV小车的运作有关，则目标规划模型可以转换为

(22)

其中，p1、p2、p3为不同目标的权重值。假设p1≫p2≫p3，即表示首先要求满足零件交货目标，在满足该目标的基础上再求解满足目标人员目标，最后考虑AGV小车数量目标。

2 基于改进分散搜索法的多目标规划模型求解

分散搜索(scatter search, SS)法[15]是一种求解整数规划的启发式算法，后来其应用范围逐步扩展到求解组合优化、非线性优化及排列等问题，并收到了较好的效果。分散搜索算法是一种基于种群进化的算法，其主要步骤包括：产生多样性的初始解、参考解集的更新、子集的产生以及子集合并和解的改进。

针对上文建立的数学模型，本文采用改进分散搜索(advanced scatter search，ASS)法进行问题的求解，与传统分散搜索法的区别主要在于：①运用遗传算法来代替以往的子集生成和合并，直接对参考集中的解进行交叉和变异，产生新解；②在解的改进中，通过采用模式搜索算法，对产生的新解进行局部搜索，加快收敛的速度。改进后的算法流程如图1所示。

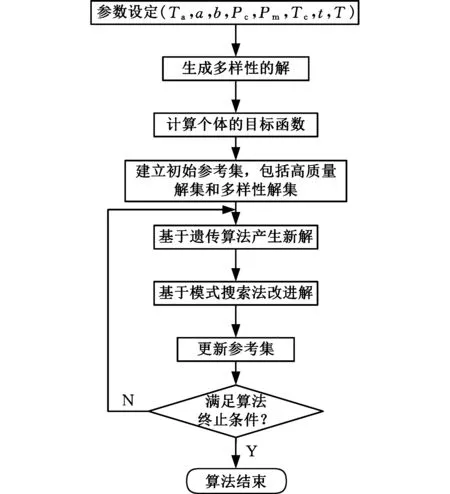
图1 算法流程图Fig.1 Algorithm flow chart

为了更好地说明算法的具体过程，本文首先提出一个简单的多资源跨单元调度问题，假设有5种零件需要在2个单元的6种设备上加工，部分零件需要在2个单元间来回加工，需用3辆AGV小车来运输，具体相关的数据关系见表1和表2。

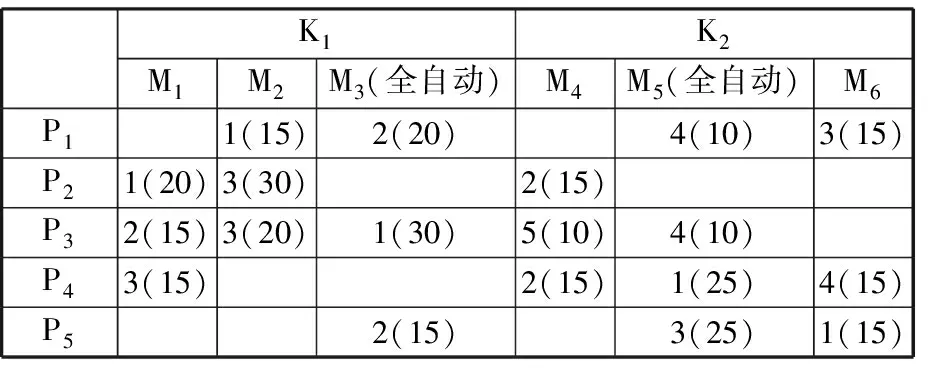
表1 设备单元划分及零件工艺过程表

注：M表示设备， P表示零件。表中数字表示零件某道工序所需的设备时间，如P1行M2列所对应的数据1(15)表示零件1的第一道工序需要设备M2，所需的时间为15 min。K1和K2表示两个不同的制造单元。

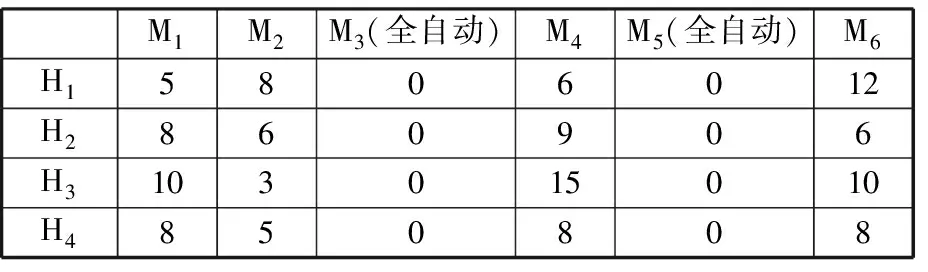
表2 员工操作设备技能一览表

注： H表示员工，表内数据表示员工操作设备的时间，min。因为全自动设备不需要员工的辅助工作，所以员工操作机器手的时间为0。

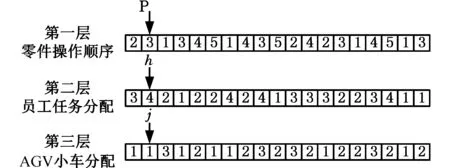
图2 编码Fig.2 Coding

第一层中的2-3-1-3-4-5-1-4-3-5-2-4-2-

3-1-4-5-1-3表示零件在设备上的排序，从P2零件的第一道工序开始加工，最后加工的是P3零件的第5道工序。第二层的人员和第三层的AGV小车分配与第一层的零件工序相对应，第二层h箭头指向的数字为4，表示零件P3的第1道工序由第4个员工操作。如果该工序是由全自动设备操作的，则可以设定该工人操作此工序的时间为0，从而符合调度模型的基本假定。第三层j箭头所指向的数字1表示P3零件的第一道工序完成后，如果需要单元间移动则选择1号AGV小车 ，如果不需要单元间转移，虽然选择了AGV小车，但由式(10)可知，其运输时间不计入零件的整个运作时间内。

(2)产生多样性解。多样性解是指解集分布的均匀性和广泛性，可以采取随机的方式产生多样性解，但是本文为了提高多样性的程度，通过设置阈值来控制多样性，从而避免产生的解过于集中。本文通过计算新入个体与已有群体内个体的欧氏距离是否超过阈值来判断该个体是否能够加入种群，从而使得种群中的个体始终保持一定的距离。欧氏距离

(23)

其中，dT为新个体与种群中第j个个体的距离；N为新产生的个体；Qj为已有种群中第j个个体。

当所有的dT≥Ta时，接受该新个体，其中Ta为阈值，可以是固定值，也可以是动态值，但是根据文献[16]的实验，动态阈值并没有获得较好的效果，因此本文采用固定阈值。

(3)个体目标函数值的计算。根据模型目标函数计算个体的目标函数：

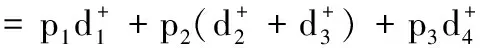
(24)

(4)建立初始参考集。在分散搜索算法中，参考集由两部分子集组成，第一部分为高质量解集Set1，第二部分为多样性解集Set2。对于高质量解集，只要计算解集中个体的目标函数，并根据目标函数值的优劣进行排序，在T个个体中选择a个最优的进入高质量解集Set1。对于初始多样性解子集，首先在剩余初始解T-a个个体中选择与高质量解集中个体欧氏距离之和最大的个体放入多样性解集Set2中，然后在剩余的个体中选择一个与现有Set1和Set2集合中个体欧氏距离之和最大的个体放入Set2中，重复此过程直到选择b个个体填充Set2集为止。

(5)产生新解。在分散搜索法中，一般采用子集合并的方法来产生新解，本文采用遗传算法产生新解，具体步骤如下：①根据轮盘赌选择法分别在高质量解集Set1和多样性解集Set2中选择一个体分别作为父代和母代；②根据一定的交叉率Pc对个体进行交叉，产生新的染色体；③根据一定的交叉率Pm对个体进行变异，产生新的染色体。

(6)解的改进。解的改进主要是对产生的多样性解集采用局部搜索的方法进行改进，本文采用模式搜索(pattern search，PS)的方法改进解，根据目标函数进行判断，当改进解的目标函数更优时，则用新解代替原有解；反之，则仍使用原有解。

模式搜索作为动态排序算法(dynamic sorted algorithm，DS)中的一种，主要是借助模式向量在当前点周围产生一组网格，如果在这些网格点中找到一个新点使目标函数值得以改善，则下一步迭代将以新点作为当前点。其基本算法步骤如下：①确定初始点并计算其目标函数。②产生网格点。网格点产生的方法是在当前点处加上m倍的模式向量，m为网格尺寸。③评价目标函数，如果发现某一网格点的函数值优于当前点，则接受该网格点为新的当前点，并将网格尺寸扩大m倍，否则当前点不变，并将网格尺寸收缩1/m，m可根据实际情况而定。④重复步骤②和③，直到满足迭代终止条件。

本节仅通过模式搜索方法进行解的优化，因此其终止条件只需满足迭代次数即可，为了减少算法的计算时间，迭代次数不宜过多，一般取2～3次。

(7)更新参考集。更新参考集是在现存参考集和改进后的新解中选择a个高质量的解，而对于多样性解的选择，除考虑多样性外，还需兼顾其目标函数值。本文设置一个阈值Tc，在现存参考集和改进后的解集中去除a个高质量解后，计算剩余解的目标函数值，将目标函数值超过阈值Tc的解按照多样性优劣排列，选择多样性最好的b个解作为多样性解集，从而将新解中优质和多样性的解加入到参考集中，剔除现存参考集中质量和多样性最差的解。

(8)算法终止准则。本文采用参考集收敛作为算法终止的标准，也就是当参考集中的个体连续t代没有发生变化时，算法终止，t≥2。

3 算法实验及算例分析

3.1算法比较

由于上述模型与前人研究具有一定差异，没有相似的标杆数据进行对比分析，故将本文所提的改进分散搜索算法(ASS)与遗传算法(GA)、分散搜素算法(SS)对不同规模的8个算例进行比较分析，应用MATLAB语言编程实现，并在Thinkpad X250计算机(运行内存4G)上实现8个算例的求解，具体可见表3。

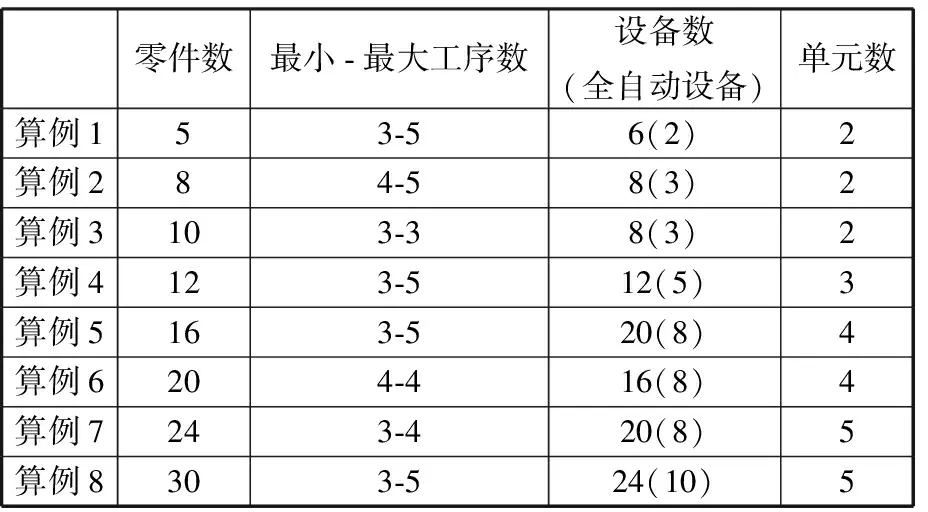
表3 算例求解信息

应用改进分散搜索算法、遗传算法以及分散搜索算法对8个算例分别求解，最终结果如表4所示，三种算法在最优解及运行时间方面的比较可见图3、图4。从表4可以看出，对于规模较小的算例，如算例1～算例3，三种算法所得结果是相同的，但是运行时间上，改进搜索算法要优于后两种算法。随着算例规模的不断扩大，改进搜索算法的最优解明显优于后两种算法，而所需运行时间的差距也逐步扩大。由此可以证明，改进搜索算法在最优解获取方面以及运算时间方面都要优于遗传算法和分散搜索算法。

表4中，PD为零件延迟时间；NW为所需工人数量；NC为所需AGV小车数量；RT为运行时间。算例1、算例2由于规模较小，故设置的个体集T和参考集的数量均较小，Set1和Set2均为10，而算例3～算例8的规模较大，故参考集的数量设置为25。

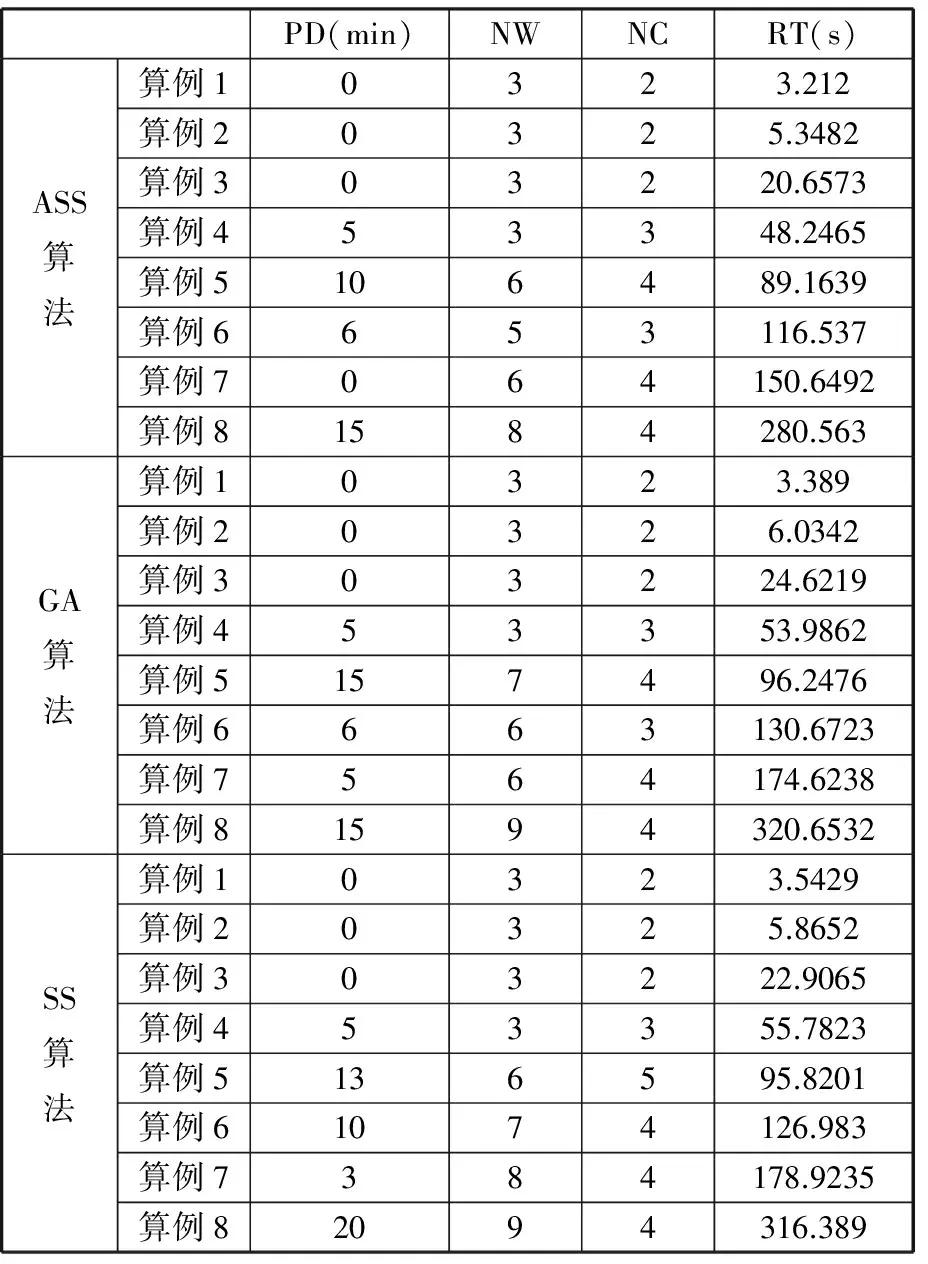
表4 三种不同算法结果比较

3.2算例分析

3.2.1算例1结果

本节根据算例1所得结果进行详细分析。算例1相关参数见表1、表2和表5，具体运算结果的甘特图见图5，从中可知不同零件各工序在不同设备上的操作顺序，以及不同设备具体操作人员的工作安排。

图5中H1，H2，H3为员工；M1，M2，…，M6为设备，其中M3和M5是全自动设备；P为零件，PX-Y则表示零件PX的第Y道工序。

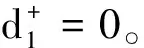
3.2.2人员对调度的影响分析

根据算例1的结果可知，员工有5次跨单元操作，关键在于H1操作M1和M4的时间较短，从而能够满足零件的交货时间。根据表2可知，如果由H3操作M1，则每次操作所需时间为10 min，远远超过了H1操作的5 min。这样的安排虽然移动次数减少了，但零件的完工时间会超过110 min的要求，如果让H4操作M1，此安排不仅会延迟零件的完工时间，也增加了员工人数。这些都直接说明了工人跨单元操作及任务分配对零件加工周期的影响。

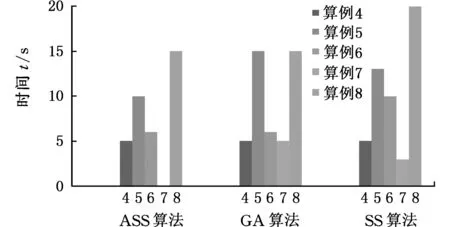
(a)PD

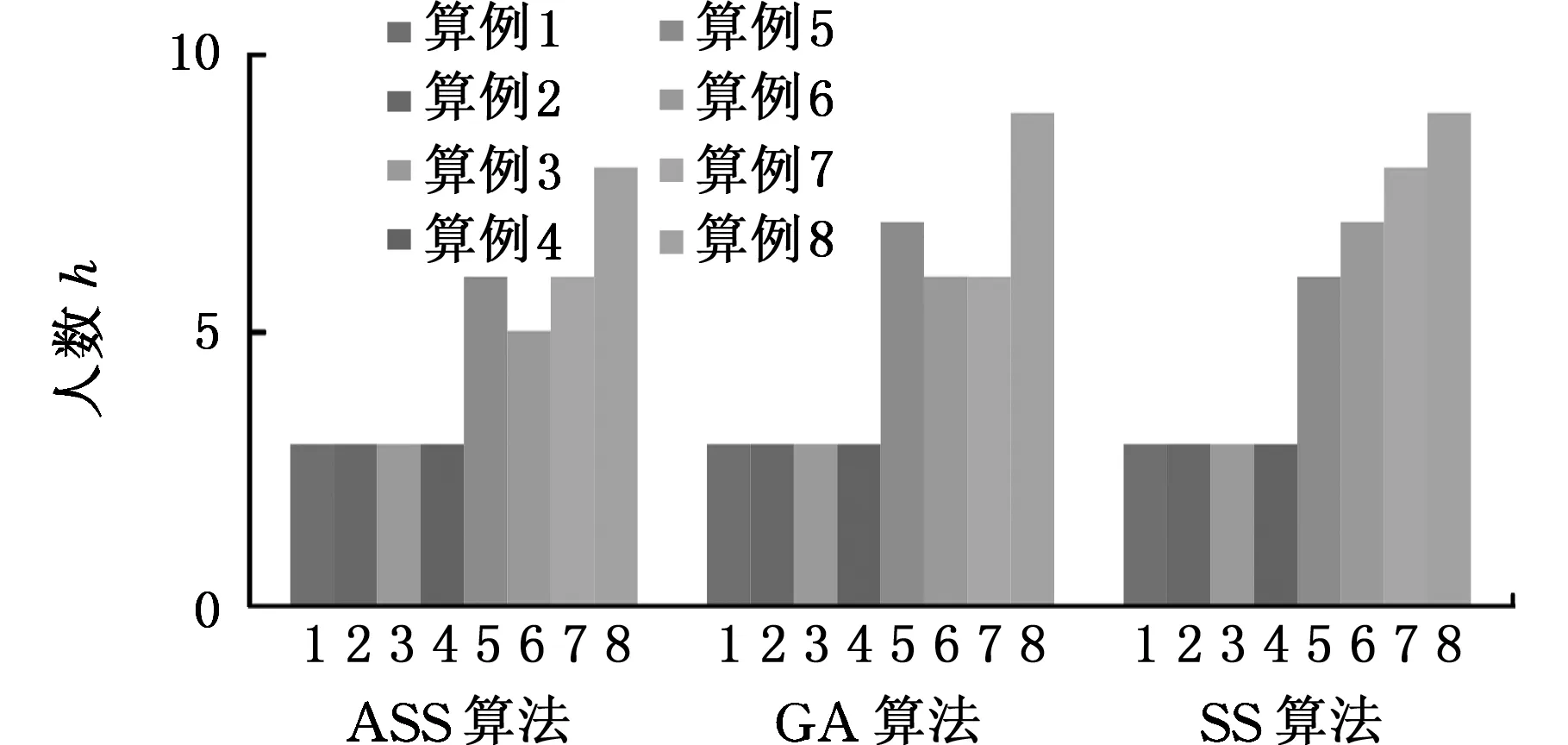
(b)NW

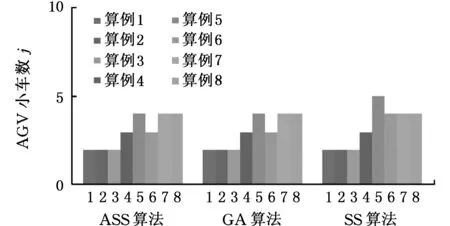
(c)NC图3 三种算法不同算例计算结果比较Fig.3 The example results comparisonunder three algorithms

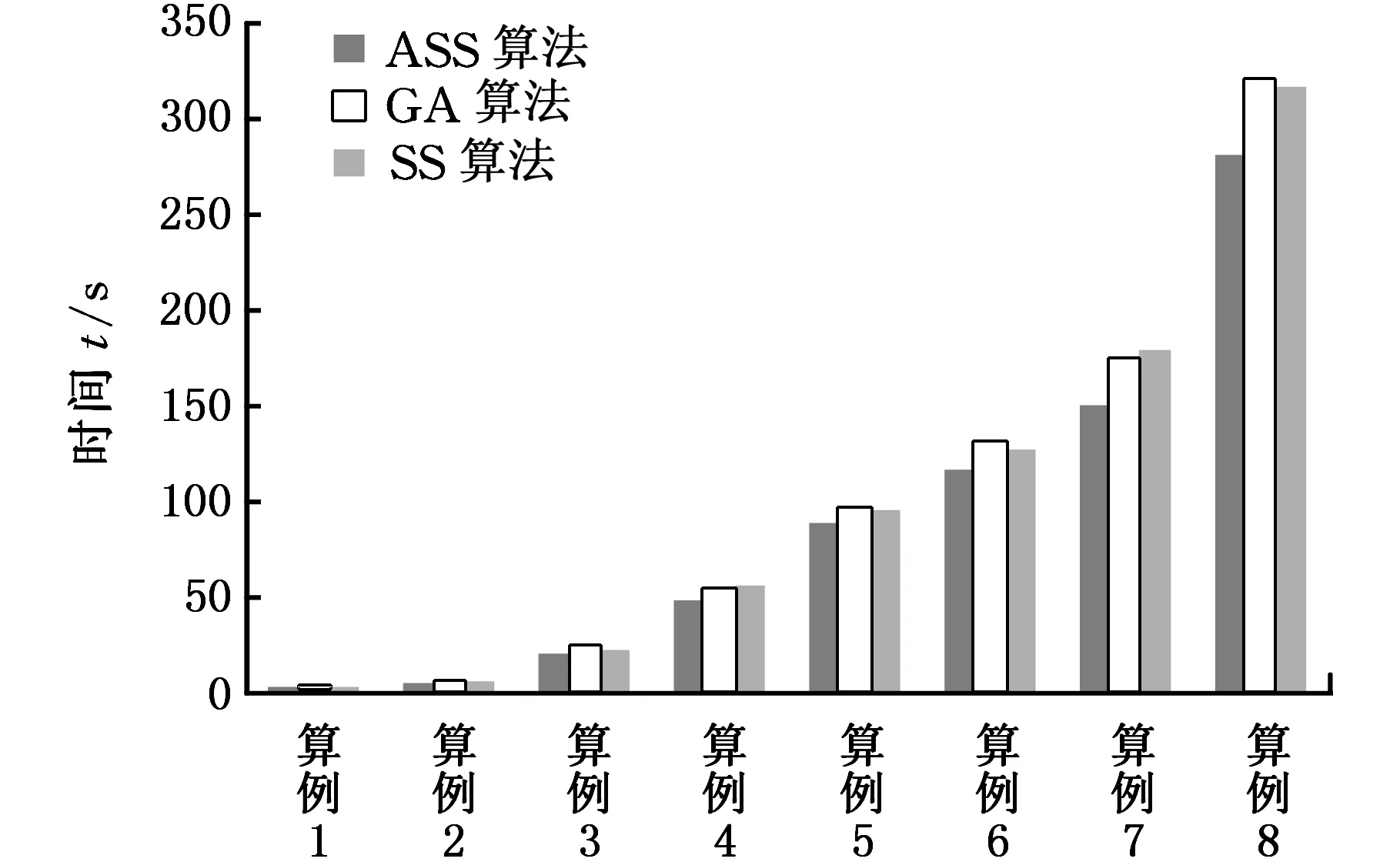
图4 三种算法不同算例运行时间比较Fig.4 The running time comparison under three algorithms

AGV单元间运输时间(min)3员工单元间移动时间(min)5零件交货时间(min)110G10G23G33G42

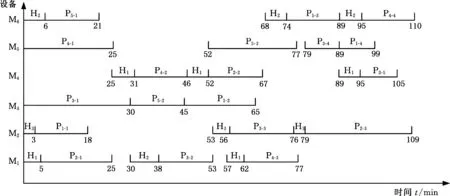
图5 零件操作顺序甘特图Fig.5 The Gantt chart of operation sequence

AGV小车序号运输零件起始位置终点位置运输起始时间(min)运输终止时间(min)零件在小车上等待至(min)运输后所在单元1P5M6M3212430C11P2M1M4303346C21P4M4M1464953C12P5M3M5454876C21P2M4M26770C12P3M2M57679C21P1M3M66568C21P4M1M6778089C2

如果将目标函数改为

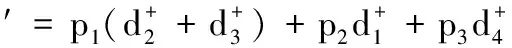
即首先保证第二和第三部分目标的要求，然后考虑第一和第四部分目标，则整个调度方案就会有微小的变化。此时为了首先保证人员目标，由H3操作M1和M2， H1操作M4，H2操作M6，员工人数仍然满足既定要求，而员工跨单元操作数量为0，同样满足要求，但是零件完工的最晚时间变为115 min，超过了既定要求。

3.2.3 AGV小车对调度的影响分析

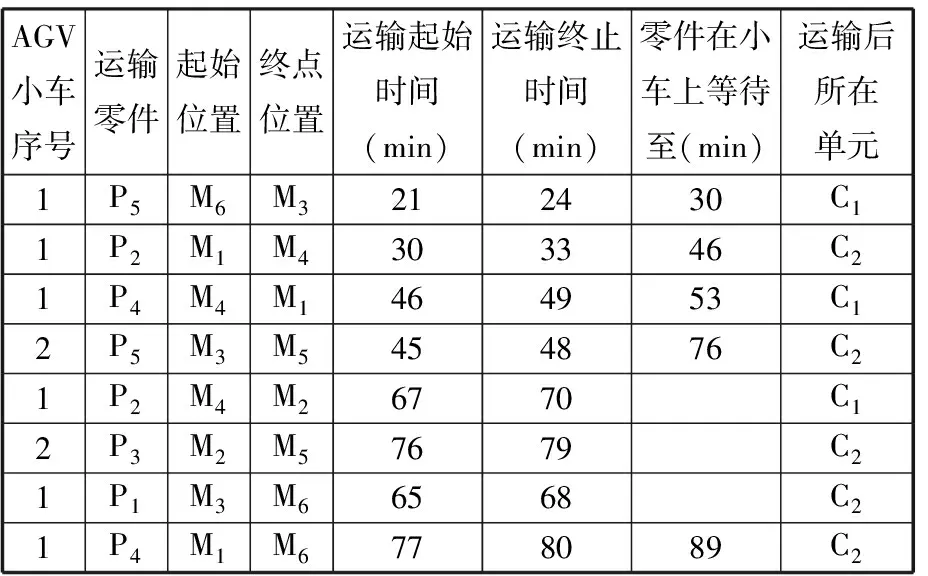
根据表6可知， AGV小车的任务分配满足了零件加工在时间上的要求。根据模型要求考虑了设备堵塞的问题，如1号AGV小车在将P4零件从C2的M4运至C1的M1的时间(49 min)，但是由于此时M1上还在加工零件P3，所以P4零件在小车上等待至P3加工完为止，也就是到53 min时，1号小车才可以使用，而在45 min时，M3上的P5必须运走，否则会影响P1-2的操作，故此时采用2号AGV小车进行运输。

假设目前企业只有1辆AGV小车，并改变目标函数:

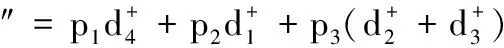
而G4=1，则整个人员安排以及操作时间都将有所变化，具体可见表7及图6所示。可以看出，此时由H1操作设备M1，H3操作设备M2，H2操作设备M6和M4，而H1只操作P3-5在M4上的加工，主要原因是只有1辆AGV小车进行零件运输，导致设备堵塞，故让H2操作M4设备，虽然操作时间增加，但是部分时间可与设备堵塞时间相抵消，另一方面也减少了员工的移动次数，所以AGV的任务安排也在一定程度上影响了人员的安排。由H1操作P3-5主要是考虑人员在同一时刻只能加工一个产品，若由H2操作P3-5会导致P4-4的完工时间达到120 min，故该处增加了人员操作的一次移动。按照该调度方案，除了P4的加工时间比规定的时间延迟了7 min外，其他情况都符合目标规划的要求。

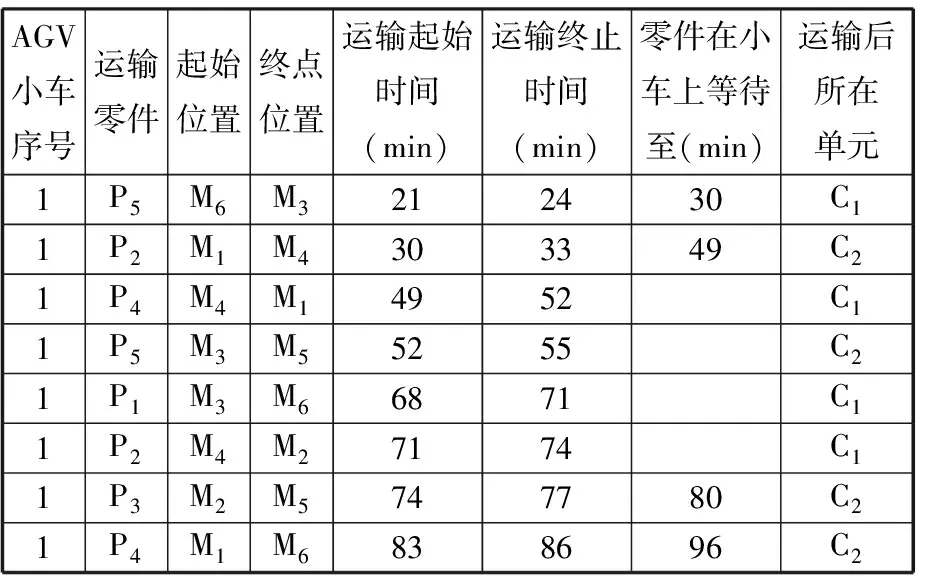
表7 AGV小车运输过程(1辆AGV小车)

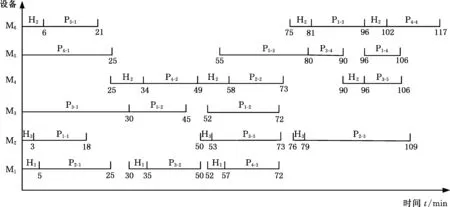
图6 零件操作顺序甘特图(1辆AGV小车)Fig.6 The Gantt chart of operation sequence(1 AGV)

4 结语

本文基于各种资源的特点以及在制造系统中的作用，在以往研究基础上，提出了多资源跨单元操作的调度问题，建立了相应的数学模型，应用改进分散搜索法求解模型，并应用于不同规模的8个案例中，在时间和求解结果方面都获得了较好的效果。

本文为了多资源跨单元调度问题的简化，假设每种零件只有一条加工工艺路径，且每一种设备类型均只有一台，这在一定程度上限制了模型在实际问题中的应用范围，因此在后续研究中，将进一步研究多工艺路径及员工流动环境下的多资源跨单元调度问题，进一步拓展单元调度问题的内涵。

[1] 于洋, 查建中, 牟建斌. 单元制造技术及其实施方法[J]. 制造业自动化, 2001, 13(4): 4-6.

YU Yang,ZHA Jianzhong, MOU Jianbin. Introduction and Implementation of Cellular Manufacturing [J]. Manufacturing Automation, 2001, 13(4): 4-6.

[2] 王跃岗，车阿大. 基于混合量子进化算法的自动化制造单元调度[J].计算机集成制造系统, 2013,19(9): 2193-2201.

WANG Yuegang, CHE Ada. Robotic Cells Scheduling Based on Hybrid Quantum Evolutionary Algorithm [J]. Computer Integrated Manufacturing Systems, 2013,19(9): 2193-2201.

[3] 韩文民, 吴满成, 王洁, 等.考虑批量分割的虚拟单元调度研究[J]. 制造业自动化, 2015,37(8):14-20.

HAN Wenmin,WU Mancheng, WANG Jie, et al. Research on Lot-streaming in Virtual Manufacturing Cellular Scheduling [J]. Manufacturing Automation, 2015,37(8):14-20.

[4] KARTHIKEYAN S, SARAVANAN M, GANESH K. GT Machine Cell Formation Problem in Scheduling for Cellular Manufacturing System Using Meta-heuristic Method[J]. Procedia Engineering, 2012, 38(5):2537-2547.

[5] 李冬妮, 肖广雪, 王妍, 等. 一种柔性路径下的跨单元调度方法[J]. 自动化学报, 2012, 38(6): 969-975.

LI Dongni, XIAO Guangxue, WANG Yan, et al. An Intercell Scheduling Approach Considering Flexible Processing Routes [J]. Acta Automatica Sinica, 2012, 38(6): 969-975.

[6] 贾凌云, 李冬妮, 田云娜. 基于混合蛙跳和遗传规划的跨单元调度方法[J]. 自动化学报, 2015, 41(5):936-948.

JIA Lingyun, LI Dongni, TIAN Yunna. An Intercell Scheduling Approach Using Shuffled Frog Leaping Algorithm and Genetic Programming [J]. Acta Automatica Sinica, 2015, 41(5):936-948.

[7] SOLIMANPUR M, ELMI A. A Tabu Search Approach for Cell Scheduling Problem with Makespan Criterion[J]. International Journal of Production Economics, 2013, 141(2): 639-645.

[8] 季少梅. 柔性路径下基于混合粒子群算法的跨单元调度方法[D].北京：北京理工大学, 2011.

JI Shaomei. Hybrid Particle Swarm Optimization Algorithm in Inter Cell Scheduling Problem with Flexible Routes [D]. Beijing: Beijing Institute of Technology, 2011.

[9] MENG X W, JU Y H, WANG X H, et al. An ACO-based Approach for Intercell Scheduling with Various Types of Machines[C]//Proceedings of the 25th Chinese Control and Decision Conference (CCDC). Guiyang, 2013:1812-1817.

[10] PAJOUTAN M, GOLMOHAMMADI A, SEIFARGHY M. CMS Scheduling Problem Considering Material Handling and Routing Flexibility[J]. The International Journal of Advanced Manufacturing Technology, 2014, 72(5/8): 881-893.

[11] 马帅. 双系统优化及约束作业车间调度应用研究[D]. 大连：大连理工大学, 2013.

MA Shuai. A Dual-system Optimization Method for Constrained Job Shop Scheduling [D]. Dalian: Dalian University of Technology, 2013.

[12] 刘旭, 楼佩煌, 钱晓明, 等. 基于改进遗传算法的物料配送多AGV 调度优化[J].机械设计与制造工程, 2015, 44(3):17-22.

LIU Xu, LOU Peihuang, QIAN Xiaoming, et al. Scheduling of Automated Guided Vehicles for Material Distribution Based on Improved Genetic Algorithm [J]. Machine Design and Manufacturing Engineering, 2015, 44(3):17-22.

[13] NISHI T, HIRANAKA Y, GROSSMANN I E. A Bi-level Decomposition Algorithm for Simultaneous Production Scheduling and Conflict-free Routing for Automated Guided Vehicles[J]. Computers and Operations Research, 2011, 38(5):876-888.

[14] FAN Jiajing, FENG Dingzhong. Design of Cellular Manufacturing System with Quasi Dynamic Dual Resource Using Multi-objective GA[J]. International Journal of Production Research, 2013, 51(14):4134-4154.

[15] GLOVER F. Heuristics for Integer Programming Using Surrogate Constraints [J]. Decision Science, 1977, 8: 156-166.

[16] 刘衍民, 赵庆祯, 邵增珍. 一种自适应多样性保持的多目标粒子群算法[J]. 济南大学学报(自然科学版), 2011, 25(3): 296-300.

LIU Yanmin, ZHAO Qingzhen, SHAO Zengzhen. Multi-objective Particle Swarm Optimizer with Adaptive Diversity Maintenance [J]. Journal of University of Jinan (Science and Technology), 2011, 25(3): 296-300.

(编辑王旻玥)

StudyonMulti-resourceIntercellularSchedulingProblemBasedonASSAlgorithm

FAN Jiajing1CAO Yuhua1CAO Min2

1.School of Economics and Management,Hangzhou,Zhejiang University of Science and Technology,Hangzhou,310023 2.School of Mechanical amp; Automotive Engineering，Zhejiang University of Science and Technology,Hangzhou,310023

An intercellular scheduling problem based on multi-resource constraint was put forward considering the characteristics and important roles of equipment, human resources and AGVs in cellular manufacturing system. Aiming at minimum sum of part late delivery times, the numbers of employee and intercellular moving times and the numbers of AGV, a goal programming mathematical model was built. An ASS algorithm was presented to solve this model according to the model particularity. In the ASS algorithm, a genetic algorithm was used to get the new solution sets and the pattern search(PS) was used to improve the reference solution sets to enhance the rate of convergence. The mathematical model and algorithm were applied into 8 different size examples to prove validity of the model and algorithm. At last, the interactions of equipment, human resource and AGV were explained based on the analyses of the examples.

intercellular; scheduling; multi-resource; advanced scatter search(ASS) algorithm

TH166

10.3969/j.issn.1004-132X.2017.22.012

2016-10-17

范佳静，女，1977年生。浙江科技学院经济与管理学院副教授、博士。主要研究方向为单元制造系统的构建、调度。出版专著1部，发表论文10余篇。 E-mail：carole_cn@163.com。曹玉华，女，1976年生。浙江科技学院经济与管理学院讲师。曹敏，女，1965年生。浙江科技学院机械与汽车工程学院教授。