基于定向距离理论的五轴加工刀具轨迹规划算法
2017-12-02尹业熙秦衡峰周后明
尹业熙 秦衡峰 周后明
1.湘潭大学机械工程学院,湘潭,4111052.湘潭大学复杂轨迹加工工艺及装备教育部工作研究中心,湘潭,411105
基于定向距离理论的五轴加工刀具轨迹规划算法
尹业熙1,2秦衡峰1周后明1
1.湘潭大学机械工程学院,湘潭,4111052.湘潭大学复杂轨迹加工工艺及装备教育部工作研究中心,湘潭,411105
针对环形刀五轴加工自由曲面的残留误差问题,在传统等残留高度算法的基础上,提出了一种基于定向距离理论的等最大残留高度刀具轨迹规划算法。首先根据微分几何理论计算已知刀触点的初始侧向行距,并在侧向行距方向进行偏置得到相邻刀触点;然后以基于定向距离理论的残高误差计算模型对相邻刀触点间的实际残高值进行计算;最后通过迭代计算规划出等最大残留高度的相邻刀具轨迹。如此循环,从而获得整个曲面的刀具轨迹。实验结果表明,相对于商用软件MasterCAM9.0,该算法在充分保证曲面加工质量的同时最大限度地减小了刀具轨迹的总长度,从而提高了加工效率。
环形刀;自由曲面;等最大残留高度;定向距离理论;刀具轨迹规划
0 引言
自由曲面五轴数控加工中,刀具轨迹的优劣和规划效率直接决定了加工精度和生产效率[1]。刀具轨迹生成的主要方法有等参数法[2]、截平面法[3]和等残留高度法[4-12]等。对于等参数法和截平面法,为了保证加工精度,在进行刀具轨迹间的行距计算时通常较为保守,使得生成的刀具轨迹分布较为密集、冗余轨迹较多、加工效率低;而等残留高度法的基本思想是在容许误差范围内控制两相邻轨迹间的残留高度相等且使得刀具的切削宽度达到最大值。传统的等残留高度法由美国SURESH等[4]提出,以允许的弓高、残高误差最大值进行刀轨的步长和行距计算,经过偏置和拟合得到覆盖整个自由曲面的刀具轨迹,在理论上可以最大限度地增加刀轨间的行距、缩短刀轨总长度,以获得最高的加工质量和加工效率。许多学者对该算法进行了优化。赵世田等[5]提出了一种改进后的等残留算法;杨长祺等[6]以消除传统等残留高度算法中对相邻刀轨在切削方向及局部几何信息的近似为目的,对传统等残留高度算法进行了优化;林志伟等[7-8]提出了基于切割曲面法矢的五轴等残高刀具轨迹生成算法。上述算法的计算思想基本都是:首先计算刀具处于已知刀触点时满足精度要求的残高点及其投影点,然后根据所求得的残高点投影点寻找相邻的刀轨,在计算过程中近似地认为所求得的残高点投影点和相邻刀轨中相对应的刀触点拥有相同的局部几何信息上述算法忽略了相邻刀触点的刀具姿态问题,对局部情况复杂的刀触点进行这种近似处理会导致很大的计算误差,使得实际残留高度可能超出容许值范围。
针对上述问题,本文以定向距离理论为基础,提出一种环形刀加工自由曲面的等最大残留高度刀具轨迹规划算法,使得加工后的实际残留高度恰好等于容许残留误差值,在充分保证曲面加工质量的基础上最大限度地加大相邻刀轨间的行距和缩短刀具轨迹总长度,从而提高加工效率。
1 定向距离理论
如图1所示,在三维空间中有两个曲面S1(u,v)、S2(u,v),若E(u1,v1)、F(u2,v2)分别表示曲面S1、S2上的任意一点,那么两曲面间的距离可表示为[13-14]:
d=inf‖E(u1,v1)-F(u2,v2)‖
(1)
其中,inf表示取范数集中的最小值,范数值‖·‖指欧氏域范数值,即对于空间上任意一点O(x,y,z),则该点的范数值可表示为

(2)
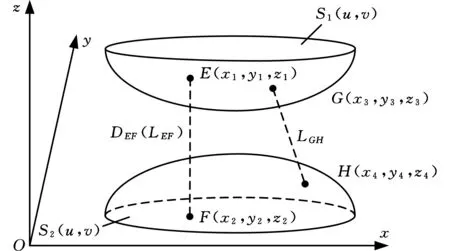
图1 定向距离模型Fig.1 Directional distance model
由泛函数分析可知,对于两个不相交的曲面,至少存在一对相对点使其距离最小;特别地,当有一对相对点间的距离为0时,那么两曲面间至少有一个交点;其中各相对点之间的距离称为有向距离。根据两点间有向距离概念可知两曲面间可以作无数条有向直线,若所作有向直线平行于一个预先给定的方向矢量,则称所作的有向直线为定向直线,其距离为定向距离,定向直线与两曲面的两个交点称为定向相对点。如图1所示,假设给定的方向矢量为坐标系中的z轴,若E(x1,y1,z1)、F(x2,y2,z2)两点分别位于两曲面S1、S2上,且E、F间的有向直线EF平行于坐标轴z轴,则称有向直线EF为定向直线,其有向距离LEF为定向距离DEF,E、F两点称为定向相对点,那么必有x1=x2、y1=y2,且定向距离DEF可表示为
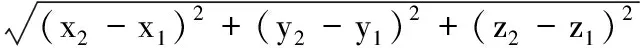
(3)
因此对定向相对点可作以下定义:
如果在坐标轴z轴方向上,两曲面S1:z=f2(x,y),S2:z=f2(x,y)上两点的x、y坐标值相等,就可称其为一对定向相对点,即若有
(4)
则称P1、P2为一对定向相对点;同理,对x=f(y,z)或者y=g(x,z)也可以作出相似的定义。事实上,一对定向相对点就是用一系列平行于某给定矢量的直线截取两曲面,所得到的两交点就是一对定向相对点,如图1所示,E、F两点为一对定向相对点,而G、H两点则不是。
2 等最大残留高度刀具轨迹规划
2.1初始侧向行距计算
在环形刀五轴加工切削中,根据微分几何理论可求得刀具位于当前刀触点(刀触点)时的有效切削半径re[9,15]为
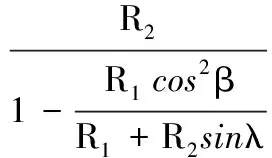
(5)
其中,R1、R2为环形刀刀具半径尺寸,如图2所示。λ、β分别为刀具姿态中的倾斜角和旋转角。
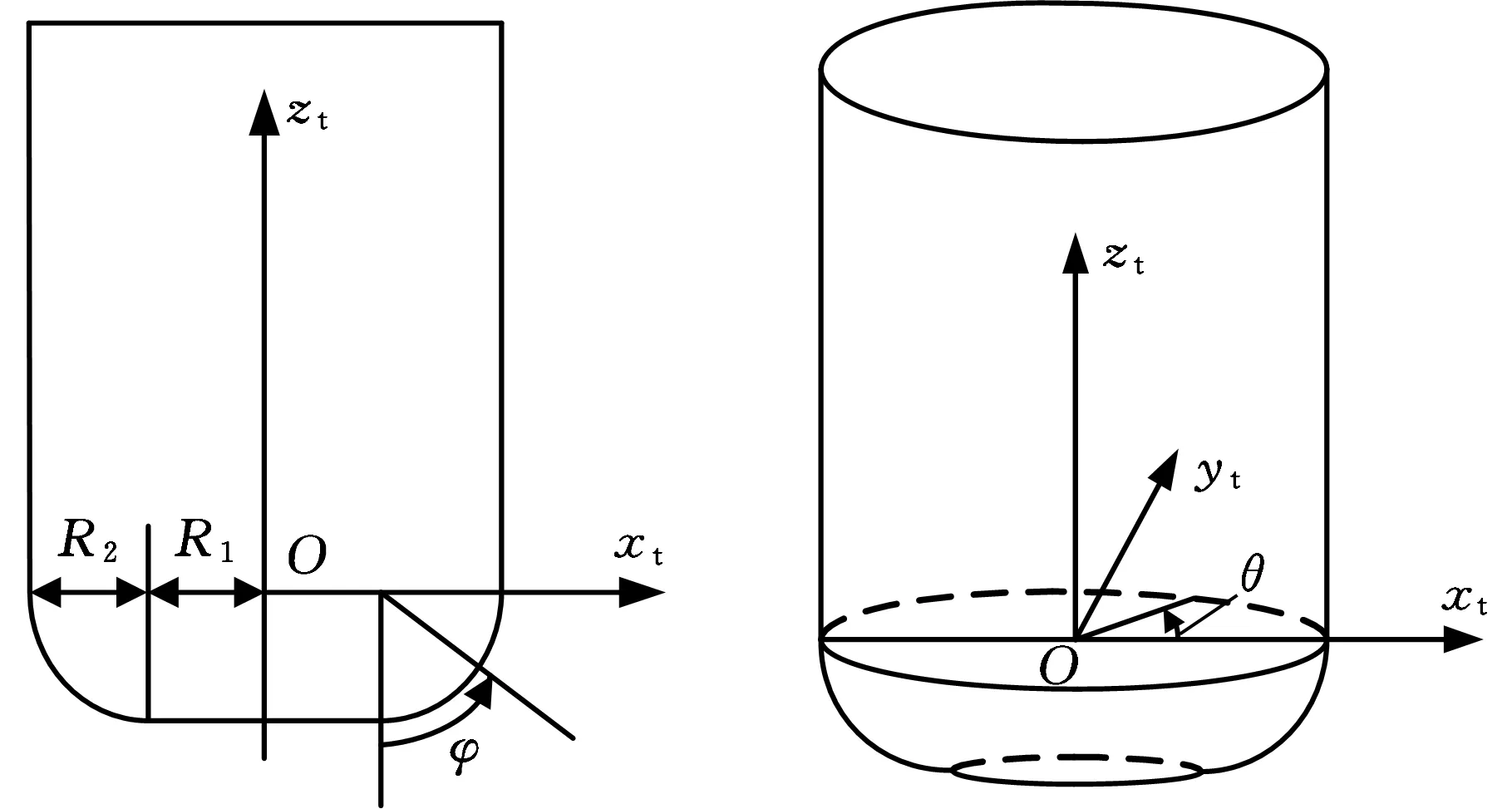
图2 环形刀与刀具局部坐标系Fig.2 Toroidal cutter and tool local coordinate system
若工件曲面在当前刀触点的法曲率半径为rb,容许残留高度误差值为δ,则可计算出行距D[9]为
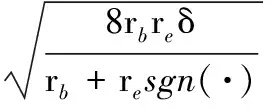
(6)
式中,sgn(·)为取值函数,当工件曲面为凸曲面时取值为1,为平面时取值为0,为凹曲面时取值为-1。
令工件曲面S(u,v)的当前刀具路径Pi=S(u(w),v(w))上的已知刀触点为Ci,j=S(u(wj),v(wj)),则与其相对应的下一刀具路径和刀触点分别为Pi+1和Ci+1,j,假设在行距方向(垂直于Ci,j点进给方向)上寻找Ci+1,j,则有
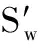
(7)
D=‖Ci+1,j-Ci,j‖
(8)
将Ci+1,j在Ci,j处按泰勒公式展开并略去二阶以后的余项,结合微分几何理论可得
(9)
式中,E、F、G为曲面的第一类基本量。
根据式(9)即可求得Ci+1,j的参数坐标值:
Ci+1,j=S(u(wj)+Δu,v(wj)+Δv)
(10)
2.2残留高度计算
在数控加工中,两相邻刀轨间刀具包络曲面所形成的交线称为残高曲线,残高曲线上的点称为残高点[16-17],计算实际残高点其实质是计算刀具位于两相邻刀轨间对应刀触点时刀具包络曲面的交点,而在CAM刀具轨迹规划中,要规划出满足精度要求的相邻刀轨,只要将已知刀轨中的所有刀触点进行精确的偏置即可,因此,可以假设该偏置过程为刀具在两刀触点间的一个平移运动,偏置方向为刀具平移过程的终结运动方向,根据包络加工理论[11,13,18]和定向距离理论[13-14],可将残高点的计算转化为在终结运动方向上两刀具切削面的定向最小距离计算,即为寻找定向相对点为一重合点的过程。
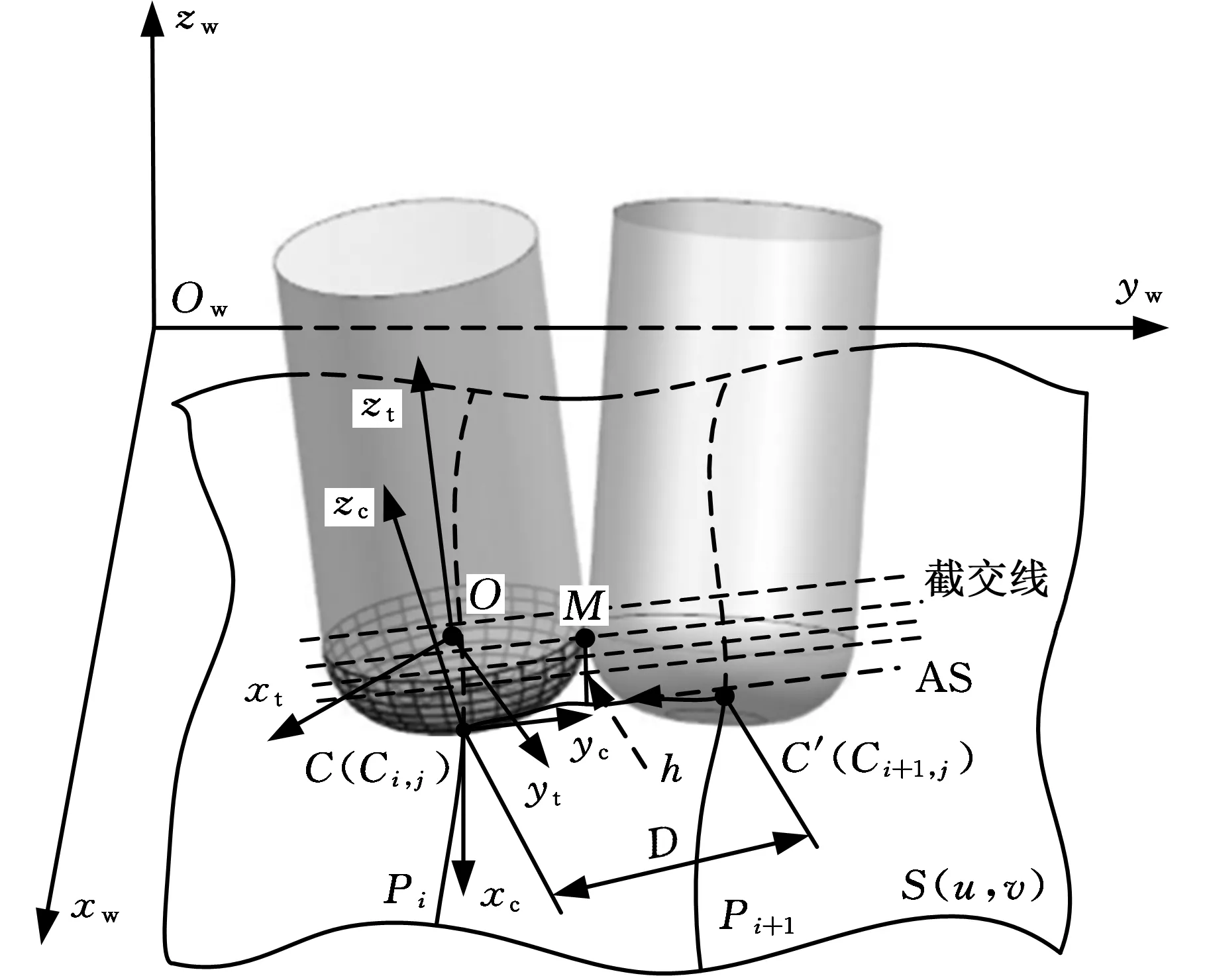
图3 残留高度示意模型Fig.3 Schematic model of scallop-height
图3所示为环形刀加工自由曲面过程中刀具位于相邻刀轨相对应的刀触点时的切削状态,S(u,v)为工件曲面,Pi、Pi+1为两相邻刀轨,坐标系Ww(Owxwywzw)和Wc(Cxcyczc)分别表示工件坐标系和位于刀触点Ci,j上的工件局部坐标系,其中,xc轴和zc轴分别表示位于当前刀触点Ci,j的进给方向(即为该刀轨Pi在参数t=ti处的切向方向)和工件曲面在Ci,j点的法矢(单位矢量为n),Ci+1,j为Pi+1刀轨上与Ci,j相对应的刀触点,AS表示Ci,j、Ci+1,j间的实际曲面曲线,D和h分别表示两相邻刀轨间的行距和残留高度值,M为残高点。假设刀触点Ci,j的刀位点(CL点)与刀轴矢量分别用O和T表示,以O点为支点绕yc轴旋转一个λ角(刀具倾斜角,λ∈(-π/2,π/2)),然后再以刀触点C为支点绕zc轴旋转一个β角(刀具旋转角,β∈(0,2π)),即可得到刀具位于Ci,j时的刀具局部坐标系Wt(Oxtytzt), 在Wt(Oxtytzt)下环形刀如图2所示,其刀具的圆环切削面参数方程可由下式表示:
(11)
ω∈(-π/2,0)θ∈(0,2π)
根据切削原理可知:计算相邻刀轨间的残留高度,其实质是计算相邻刀轨中所有相对应的刀触点间的残留高度,现以计算刀触点Ci,j、Ci+1,j间的残留高度为例进行描述。
2.2.1残高点计算
根据图2,刀触点Ci+1,j由已知刀触点Ci,j向yc轴方向偏置一个初始行距D所得,位于该点的进给方向f′可表示为
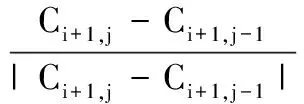
(12)
式中,Ci+1,j-1与Ci+1,j为同一刀轨的相邻刀触点。
在Ci+1,j点按上述方法建立工件局部坐标系Wc′(C′xc′yc′zc′)和刀具局部坐标系Wt′(O′xt′yt′zt′),由式(11)可得刀具位于Ci,j、Ci+1,j点时的刀具切削面参数表达式Ti,j(ω,θ)、Ti+1,j(ω,θ),假设Ci,j、Ci+1,j的刀具姿角分别为(λ,β)、(λ′,β′),通过坐标平移、旋转可得到在坐标系Wc(Cxcyczc)中的参数表达式:
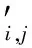
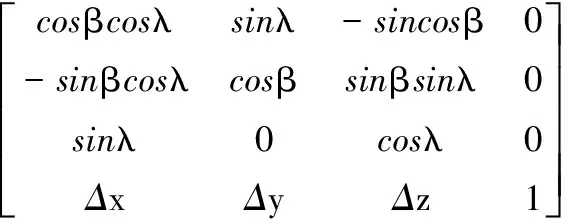
(13)
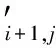
(14)
式中,α、γ分别为yc轴与yc′轴、zc轴与zc′轴的夹角;Δx、Δy、Δz为刀具位于Ci点时刀位点到Ci点的平移距离;Δx′、Δy′、Δz′为刀具位于Ci+1点时刀位点到Ci+1点的平移距离。
在坐标系Wc(Cxcyczc)中,令刀具位于Ci,j、Ci+1,j点的切削面分别为曲面A、B,根据定向相对点定义,要求两曲面在终结方向yc轴方向上的定向相对点,其实质是用一系列平行于yc轴的截交线分别截曲面A、B,其交点即为在yc轴方向上的定向相对点。假设某截交线与曲面A上的交点为M(x,y,z),若曲面B存在一点N与其为定向相对点,那么N点的坐标值定为N(x,y′,z)。根据上述对残高点计算的转化可知,若某定向相对点为刀触点Ci,j与Ci+1,j间形成的残留高度的残高点,那么该定向相对点必定为一重合点,即M、N两点的x、y、z坐标值全都相等,此时将出现以下三种情况:
(1)不存在符合条件的定向相对点。刀具分别位于刀触点Ci,j、Ci+1,j进行包络加工后,两刀触点间仍有一部分区域刀具无法对其进行切削,很显然,该情况下所产生的残留高度必然会大于残留高度允许值,此时残高点输出为空集。
(2)存在符合条件的定向相对点且仅有一个。刀具位于刀触点Ci,j、Ci+1,j进行包络加工时,两刀具切削面在该定向相对点处接触且相切,则此定向相对点为所求残高点。
(3)存在符合条件的定向相对点且不止有一个。刀具位于刀触点Ci,j、Ci+1,j进行包络加工时,两刀具切削面相交,此时选取符合条件的定向相对点中z坐标轴值最小的点作为残高点。
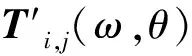
2.2.2残留高度计算
已知残高点计算残留高度的过程,其实质是计算残高点M到该点在工件曲面上垂足点的距离。若点Q(uQ,vQ)为S(u,v)上的任意一点,其偏导数为SuQ和SvQ,如图4所示,根据微分几何理论,其领域内的点P(up,vp)可表示为
P=Q+ΔuSuQ+ΔvSvQ
(15)
其中,当Δu=0,Δv=0时,P、Q两点为曲面上的重合点。
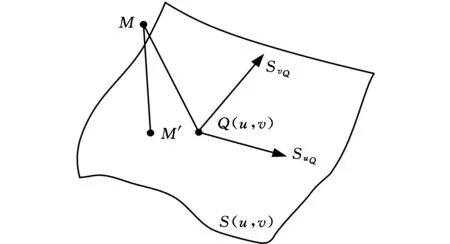
图4 残留高度计算模型Fig.4 Calculation model of scallop-height
那么M到Q的有向线段可表示为
MQ=Q-M+ΔuSuQ+ΔvSvQ
(16)
将式(16)两边同时乘以SuQ和SvQ可得
(17)
理论上,如果Q为残高点M在曲面的垂足点,那么MQ与曲面垂直,则一定有
(18)
因此,若满足式(18),则Q为残高点M在工件曲面S(u,v)上的垂足点M′,MQ间的距离即为残留高度;若不成立,根据式(17)计算Δu、Δv,在曲面上以Q(uQ,vQ)为起点、(Δu,Δv)为步长寻找下一可能满足要求的点Qi+1,直到满足式(18)停止迭代;在残留高度计算时可以选择Ci,j或Ci+1,j作为迭代起点进行迭代计算。
综上所述,残留高度h计算流程如图5所示。
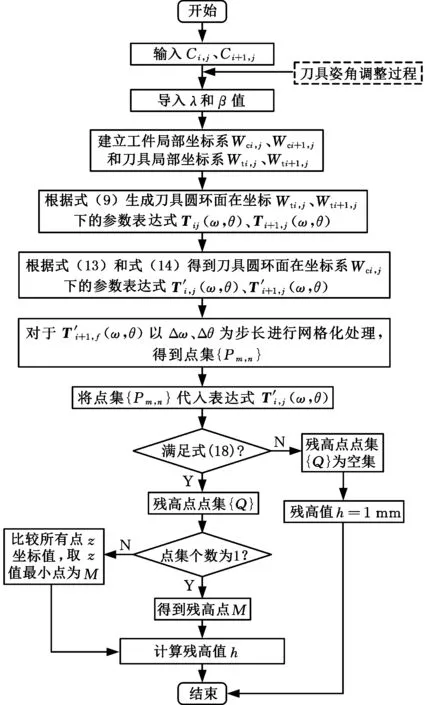
图5 残留高度h计算流程Fig.5 Calculation procedure of scallop-height h
2.3刀具轨迹规划
设工件曲面为S(u,v),以参数方向u=0的曲面边界曲线作为初始刀具轨迹线,记为Pi(u(t),v(t)),Pi,1,Pi,2,…,Pi,n-1,Pi,n为初始刀具轨迹线上的刀触点,根据这些已知刀触点,利用等最大残留高度方法来确定下一条刀具轨迹线Pi+1上的刀触点Pi+1,1,Pi+1,2,…,Pi+1,n-1,Pi+1,n,残留高度误差允许值为δ,为了使行距在残留高度误差允许值内达到极限值,设置残留高度差值的迭代阈值为h′,则等残留高度轨迹线计算流程如下:
(1)对刀触点Pi,n在参数方向v向上偏置一个初始行距D的距离得到相邻刀轨Pi+1上的刀触点Pi+1,1,按式(10)计算点Pi+1,1参数坐标值u,并比较u与1的大小,若u≤1,则ui+1,1=u,否则取ui+1=1。
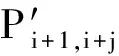
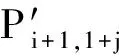
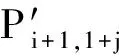
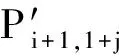
(6)对最终确定的刀触点进行曲线插值,得到第i+1条刀具轨迹线Pi+1(u(t),v(t))。
(7)重复步骤(1)~步骤(6)直到生成的刀具轨迹线覆盖整个工件曲面。
综上,等残留高度刀具轨迹规划流程如图6所示。
3 实例分析
对图7所示的自由曲面进行刀具轨迹生成,所选的环形刀半径为R1=2.5 mm,R2=2.5 mm,残留高度差值的迭代阈值为h′=0.001 mm,刀具倾斜角和旋转角分别为λ=10°,β=0°。以参数方向u=1的曲面边界曲线为初始刀轨,初始刀轨的刀触点采用圆弧近似法进行规划,其容许弓高误差值ε=0.02 mm,同时在相同的规划参数情况下,利用商用软件MasterCAM 9.0对该自由曲面进行刀具轨迹生成。当容许残留高度值δ取值分别为0.01 mm、0.02 mm和0.04 mm时,其两种方法刀轨规划结果的参数对比如表1所示,若取δ=0.02 mm,其规划出的刀具轨迹曲线如图8、图9所示。
由上述刀轨规划过程可知,本文算法在进行刀轨规划时可以极大地减小刀轨的总长度、加大刀轨的侧向行距。对上述两种刀具轨迹进行后置处理并在Vericut软件上进行五轴加工仿真,半精加工后的仿真时间如表2所示,仿真结果如图10所示。确认刀具轨迹无误后,在Mikron UCP800 Duro双回转工作台AC型五轴加工中心进行实验验证,其半精加工结果如图11所示,通过与表面粗糙度对比样块进行对比,其半精加工后的工件表面粗糙度均可定为Ra=3.2 μm。从实际加工结果可以看出,相对于MasterCAM 9.0,本文算法规划的刀具轨迹加工自由曲面后的刀具切削路径和残留分布较为均匀,保证了自由曲面的加工表面质量。

图6 刀具轨迹规划流程Fig.6 Tool path planning flow
4 结论
(1)提出了一种基于定向距离理论的环形刀加工自由曲面刀具轨迹规划算法,首先根据定向距离理论精确计算相邻刀轨中相对应的刀触点间实际残留高度,根据容许误差值对初始行距进行精确修正,获得最大限度的加工行距,充分的利用环形刀的有效切削宽度。
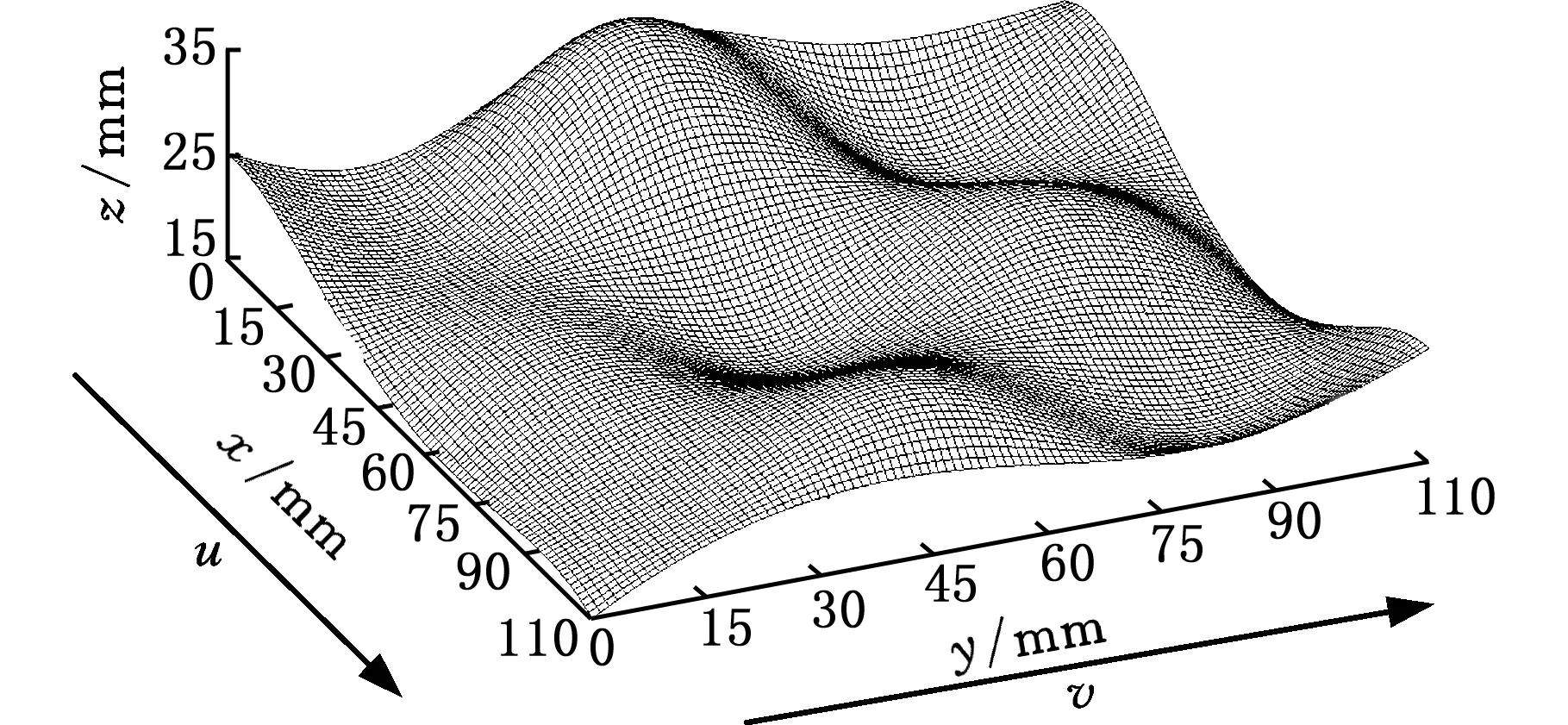
图7 原自由曲面Fig.7 Original free-surface
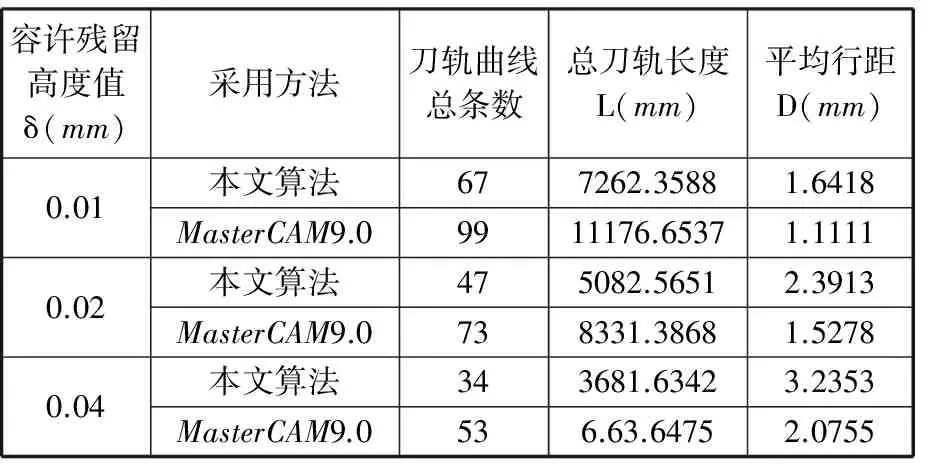
容许残留高度值δ(mm)采用方法刀轨曲线总条数总刀轨长度L(mm)平均行距D(mm)0.01本文算法677262.35881.6418MasterCAM9.09911176.65371.11110.02本文算法475082.56512.3913MasterCAM9.0738331.38681.52780.04本文算法343681.63423.2353MasterCAM9.0536.63.64752.0755
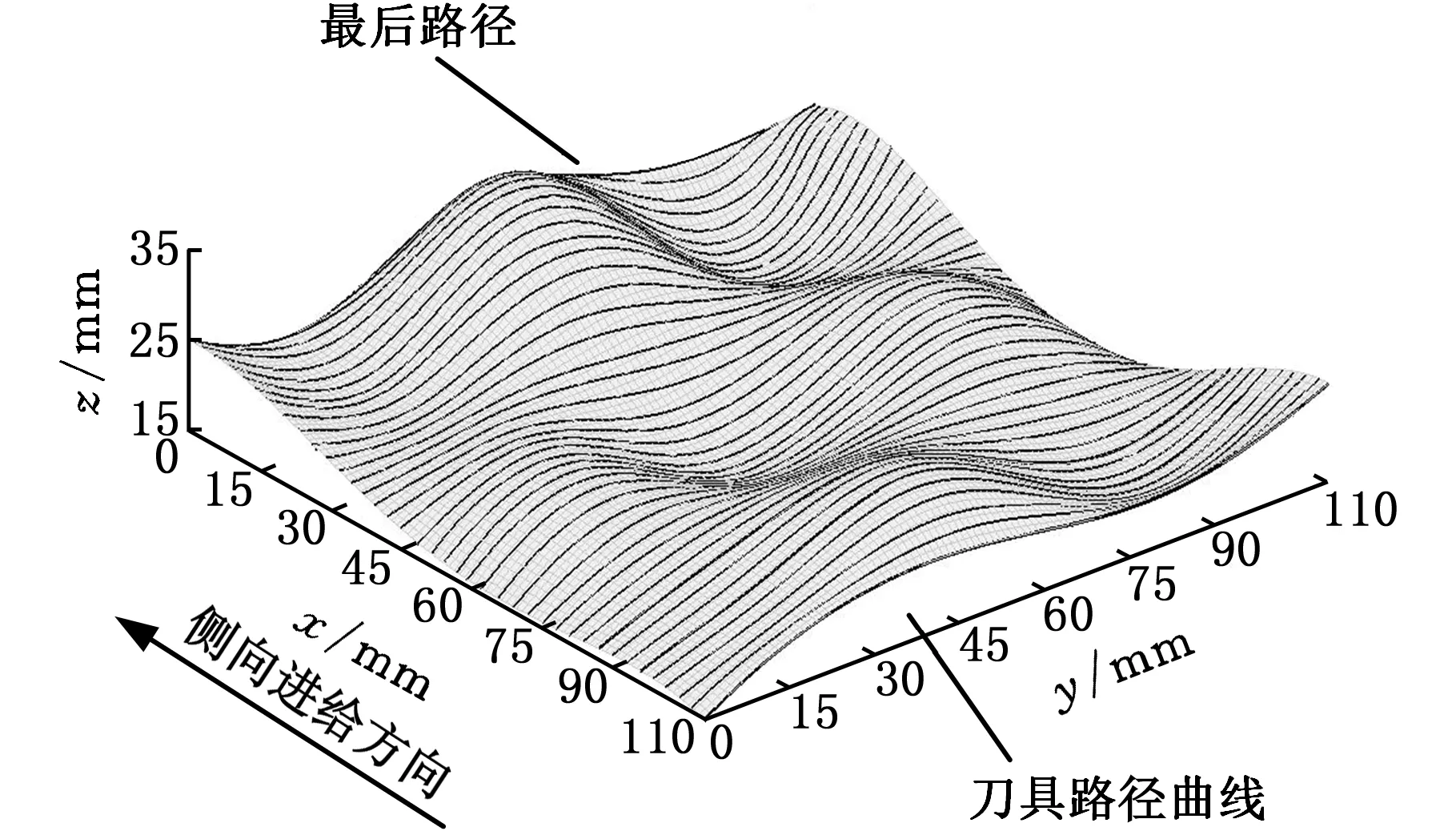
图8 本文算法刀轨规划图Fig.8 The tool-path planning of the proposed algorithm
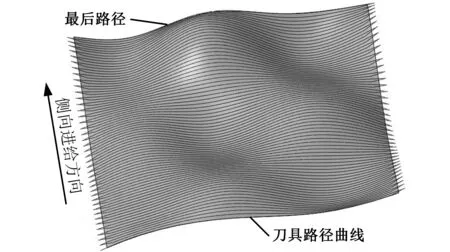
图9 MasterCAM 9.0刀轨规划图Fig.9 The tool-path planning of MasterCAM 9.0

方法本文算法MasterCAM9.0方法仿真时间54min3s1h17min24s

(a)本文方法
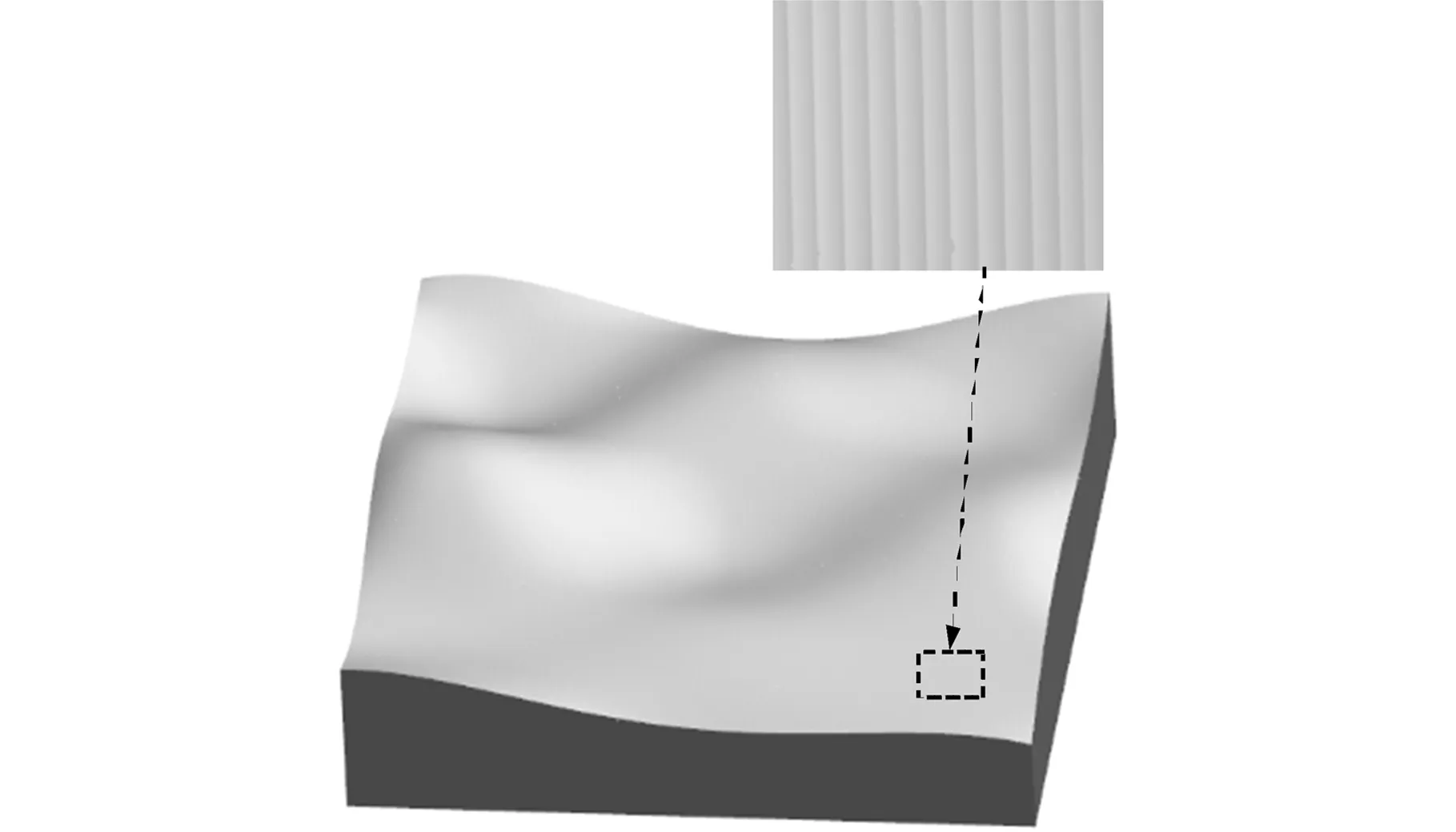
(b)MasterCAM 9.0方法图10 Vericut仿真加工结果Fig.10 Vericut simulation results

图11 实际加工结果Fig.11 Actual machining results
(2)本文算法相对于商用软件MasterCAM 9.0生成的刀轨总长度和加工仿真时长分别减少了38.99%和29.87%。
(3)采用本文算法生成刀具轨迹时,不存在工件曲面形状、环形刀具尺寸及切削形态等方面的假设,适用于任意尺寸的环形刀以及各种形状的自由曲面刀具轨迹规划,算法通用性好。
(4)实验结果表明,该研究提供了一种自由曲面加工刀路规划的方法,此方法生成的刀轨在加工自由曲面后刀具切削路径和残留高度分布较为均匀,既能充分地保证自由曲面的表面质量,又能提高加工效率。
[1] 梁媛,孙建业,王国勋. NURBS曲面五轴加工刀具规迹生成技术研究[J]. 工具技术,2014,48(7):37-42.
LIANG Yuan, SUN Jianye, WANG Guoxun. Research of Five Axis Machining Tool Trajectory Planning of NURBS Surface[J]. Tool Engineering, 2014,48(7): 37-42.
[2] LONEY G C, OZSOY T M. NC Machining of Free Form Surfaces[J]. Computer-Aided Design, 1987, 19(2):85-90.
[3] HUANG Y, OLIVER D J H. Non-constant Parameter NC Tool Path Generation on Sculptured Surfaces[J]. The International Journal of Advanced Manufacturing Technology, 1994, 9(5):281-290.
[4] SURESH K, YANG D C H. Constant Scallop-height Machining of Free-form Surfaces[J]. Journal of Engineering for Industry, 1994, 116(2):253-259.
[5] 赵世田, 赵东标, 付莹莹,等. 改进的等残余高度加工自由曲面刀具路径生成算法[J]. 南京航空航天大学学报, 2012, 44(2):240-245.
ZHAO Shitian, ZHAO Dongbiao, FU Yingying, et al. Improved ISO-scallop Tool Path Generation Algorithm for Free-Form Surface Machining[J]. Journal of Nanjing University of Aeronautics amp; Astronautics, 2012, 44(2):240-245.
[6] 杨长祺, 秦大同, 石万凯. 自由曲面五轴等残余高度高精度加工的路径规划[J]. 计算机辅助设计与图形学学报, 2003, 15(5):621-625.
YANG Changqi, QIN Datong, SHI Wankai. Precision Constant Scallop-height Tool-path Planning for Five-axis Free-form Surface Machining[J]. Journal of Computer-Aided Design amp; Computer Graphics, 2003, 15(5):621-625.
[7] Lin Z, FU J, SHEN H, et al. Tool Path Generation for Multi-axis Freeform Surface Finishing with the LKH TSP Solver [J]. Computer-Aided Design, 2015, 69:51-61.
[8] 林志伟. 五轴数控加工无干涉无奇异高效轨迹生成与优化研究[D].杭州:浙江大学,2014.
LIN Zhiwei. Research on Non-interference Non-singular Efficient Tool Path Planning and Optimization for Five-axis Machining[D]. Hangzhou:Zhejiang University, 2014.
[9] 陈良骥, 程俊伟, 王永章. 环形刀五轴数控加工刀具路径生成算法[J]. 机械工程学报, 2008, 44(3):205-212.
CHEN Liangji, CHENG Junwei, WANG Yongzhang. Tool Path Generation Algorithm for Five-axis NC Machining with a Toroidal Cutter[J]. Chinese Journal of Mechanical Engineering, 2008, 44(3):205-212.
[10] 王进波. 复杂曲面无干涉刀具轨迹生成算法研究[D]. 武汉:武汉工程大学, 2013.
WANG Jinbo. Study of the Algorithm of Interference-free Tool Trajectory Generation of Complex Surface[D]. Wuhan:Wuhan Insitute of Technology,2013.
[11] 杨旭静, 王小芳, 郑娟,等. 基于包络面的网格曲面等残留高度路径规划[J]. 湖南大学学报(自科版), 2013, 40(10):38-42.
YANG Xujing, WANG Xiaofang ,ZHENG Juan, et al. Constant Scallop-height Tool Path Generation for Mesh Surface Based on Tool Envelope Surface[J]. Journal of Hunan University(Natural Sciences), 2013, 40(10):38-42.
[12] 王太勇, 张志强, 王涛,等. 复杂参数曲面高精度刀具轨迹规划算法[J]. 机械工程学报, 2007, 43(12):109-113.
WANG Taiyong, ZHANG Zhiqiang, WANG Tao, et al. High Precision Tool Path Planning Algorithm for Complex Parametric Surface[J]. Chinese Journal of Mechanical Engineering, 2007, 43(12):109-113.
[13] 王建军. 汽轮机叶片圆环形盘铣刀包络加工理论研究[D]. 沈阳:沈阳工业大学, 2015.
WANG Jianjun. Research on Circular Disk Cutter Envelop Milling Theory for Turbine Blade[D]. Shenyang:Shenyang University of Technology, 2015.
[14] 喻德生. 平面有向几何学[M]. 北京:科学出版社, 2014.
YU Desheng. Plane Geometrical Geometry[M]. Beijing:Science Press,2014.
[15] 陈涛, 罗宏志, 钟毅芳,等. 基于曲率的曲面加工刀位轨迹生成算法[J]. 图学学报, 2001, 22(2):29-34.
CHEN Tao, LUO Hongzhi, ZHONG Yifang, et al. Curvature Based Algorithm of Cutter Location Path Generation for NC Machining of Freeform Surfaces[J]. Journal of Engineering Graphics, 2001, 22(2):29-34.
[16] CAO S K, DENG Y H, ZHANG K, et al. Free Surface NC Machining Tool Path Optimization Algorithm Based on the ISO-Scallop Method[J]. Applied Mechanics amp; Materials, 2015, 799/800:1193-1196.
[17] LIU Z, LU H, YU G, et al. A Novel CNC Machining Method for Enveloping Surface[J]. The International Journal of Advanced Manufacturing Technology, 2016(1):1-12.
[18] 严思杰, 周云飞, 陈学东. 五轴NC加工中刀具运动包络面的计算[J].中国机械工程, 2005, 16(23):2120-2124.
YAN Sijie, ZHOU Yunfei, CHEN Xuedong. Calculation for the Cuter Envelope Surface in 5-axis NC Machining[J]. China Mechanical Engineering, 2005, 16(23):2120-2124.
(编辑王旻玥)
ToolPathPlanningAlgorithmofFive-axisMachiningBasedonDirectionalDistanceTheory
YIN Yexi1,2QIN Hengfeng1ZHOU Houming1
1.School of Mechanical Engineering,Xiangtan University,Xiangtan,Hunan,411105 2.Engineering Research Center of Complex Track Processing Technology and Equipment, Ministry of Education,Xiangtan University,Xiangtan,Hunan,411105
For the residual error problems of five-axis machining free-form surface of toroidal cutter, a tool path planning algorithm with maximum ISO-scallop due to directional distance theory was proposed based on traditional ISO-scallop algorithm. Firstly, the initial lateral spacing distance of the known cutter contact (CC) point was calculated according to differential geometry theory, and the adjacent CC point was obtained in lateral direction. And then the actual scallop height of the adjacent CC point was calculated by scallop error calculation model based on the directional distance theory. Finally, the maximum ISO-scallop of the adjacent tool path was planned through the iterative calculation. Repetitions went on until the tool paths of the whole surface were obtained. The experimental results show that compared with the commercial software MasterCAM 9.0, the algorithm may greatly reduce total length of tool paths while ensuring the quality of surface machining, and improving the processing efficiency.
toroidal cutter; free-form surface; maximum ISO-scallop; directional distance theory; tool path planning
TG659
10.3969/j.issn.1004-132X.2017.22.006
2017-05-03
国家自然科学基金资助项目(51375418);湖南省自然科学基金资助项目(2017JJ4038)
尹业熙,男,1990年生。湘潭大学机械工程学院硕士研究生。主要研究方向为数控系统轨迹规划。秦衡峰(通信作者),男,1973年生。湘潭大学机械工程学院副教授。E-mail: qinhfxtu@sina.cn。周后明,男,1970年生。湘潭大学机械工程学院教授。
