一种改进的SCARA机器人动力学参数辨识方法
2017-12-02白瑞林
严 浩 白瑞林 吉 峰
1.江南大学轻工过程先进控制教育部重点实验室,无锡,2141222.无锡信捷电气股份有限公司,无锡,214072
一种改进的SCARA机器人动力学参数辨识方法
严 浩1白瑞林1吉 峰2
1.江南大学轻工过程先进控制教育部重点实验室,无锡,2141222.无锡信捷电气股份有限公司,无锡,214072
针对SCARA机器人动力学参数辨识问题,提出了一种基于优化改进傅里叶级数的辨识方法。根据SCARA机器人完整动力学方程,推导得到动力学模型的线性形式。采用改进傅里叶级数作为机器人关节的激励轨迹,使得关节角度满足连续周期性,并且关节角速度和角加速度在轨迹起始和停止时刻为零。为进一步提高辨识精度,以SCARA机器人观测矩阵的条件数为目标函数,采用基于排挤机制的小生境遗传算法对激励轨迹的系数进行优化。考虑到测量噪声的影响,采用加权最小二乘法(WLS)作为参数估计方法。实验结果表明,采用所提方法能准确辨识出SCARA机器人的动力学参数,两关节力矩测量值和预测值的残差均方根分别减小了11.50%和26.35%。
机器人;动力学;小生境遗传算法;激励轨迹;参数辨识
0 引言
随着工业机器人应用于生命医疗、激光焊接、汽车电子等高精密领域[1-2],机器人技术向高速高精度方向发展。目前,国产工业机器人大部分仍采用传统PID控制策略,难以实现高精度控制。设计基于机器人动力学模型的控制策略是实现高速高精度运动控制的有效方法[3-4],但该类控制策略要以机器人的精准动力学参数为基础。
机器人动力学参数的获取方法可分为解体测量法、CAD法以及整体辨识法。机器人结构复杂,很多参数难以通过直接测量得到。采用计算机建模的CAD法忽略了机器人的装配误差和材料的分布特性;整体辨识法能够考虑机器人实际工作中的各种因素影响,因而受到了广泛关注[5-6]。
机器人动力学参数辨识包括6个步骤:动力学建模、模型线性化、激励轨迹优化、数据采样与处理、参数估计方法、试验验证[7]。ATKESON等[8]构造5次多项式作为关节空间的激励轨迹,并采用最小二乘法作为动力学参数估计方法。SWEVER等[9]提出基于周期性傅里叶级数的辨识方法,使得机器人可以循环执行激励轨迹。但传统傅里叶级数无法保证各关节的角速度和角加速度在轨迹的起始和停止时刻为零,导致机器人在执行激励轨迹时存在抖动。同时由于采样误差的存在,由未经优化的傅里叶级数得到的观测矩阵会放大采样误差的影响[10]。丁亚东等[11]针对多关节机器人的动力学参数辨识,提出一种分步辨识方法,降低了辨识方程复杂性。陈恩伟等[12]探讨了人工神经网络在动力学参数辨识中的一般规律,使神经网络的结构与权值具有明确物理意义,但仅分析了机器人末端连杆惯性参数的辨识问题。
为了提高SCARA机器人的动力学参数辨识精度,本文对传统傅里叶级数进行改进,使得关节角速度和角加速度在轨迹起始和停止时刻为零。同时,以观测矩阵的最小条件数作为目标函数,采用基于排挤机制的小生境遗传算法对傅里叶级数的系数进行优化,降低采样误差对辨识精度的影响。为进一步降低采样误差的影响,采用加权最小二乘法对动力学参数进行辨识。
1 动力学模型及其线性化
对于n关节的机器人系统,考虑关节摩擦的影响,其动力学方程可以用二阶非线性微分方程来表示[13]:
(1)

SCARA机器人第3、第4关节共用一个连杆,第2、3、4关节的伺服电机、同步带、滚珠丝杠、升降台等都安装在关节2的连杆上,因此,关节1、关节2决定SCARA机器人的平面定位精度和轨迹跟踪精度,关节3决定竖直方向上的运动。由于关节3与前两关节垂直,所以前两关节的运动不会对关节3产生影响。由此,仅对关节1和关节2进行动力学建模及动力学参数辨识。式(1)的标量表达式如下:
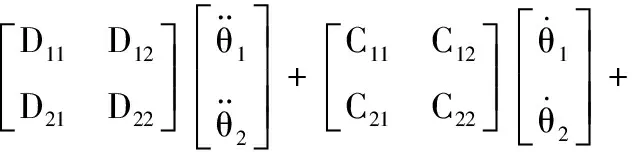
(2)
根据SCARA机器人结构,利用拉格朗日法对SCARA机器人进行动力学建模[14],得到式(2)中的各项参数:

式中,m1、m2分别为连杆1和连杆2的质量;l1、l2分别为连杆1和连杆2的长度;(x1,y1,z1)、(x2,y2,z2)分别为前两连杆的质心在坐标系1和坐标系2中的位置坐标;IZz1、IZz2分别为连杆1和连杆2沿Z轴的转动惯量;fci和fvi分别表示第i关节的库仑摩擦因数和黏性摩擦因数。
文献[15]已经证明存在一依赖于机器人参数的参数向量,使得机器人动力学方程可以线性化,即
(3)

根据式(2)的SCARA机器人动力学方程具体形式,得到线性化方程的显式表达如下:
(4)
式中各项参数如下:
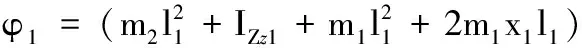
机器人动力学参数辨识实验过程为:机器人各关节跟踪特定的激励轨迹,通过采样或间接计算得到关节的输入力矩、关节角度、角速度、角加速度,估计动力学参数φ。机器人各关节跟踪激励轨迹时,在采样时刻t1,t2,…,tN对关节输入力矩等进行N次直接或间接采样,则可以得到如下方程:
YNφ=τN
(5)
即
(6)

2 激励轨迹优化设计
采用周期性的傅里叶级数作为激励轨迹,能充分激励机器人的动力学特性,并且多次采样取均值可以提高信噪比。但在轨迹的起始和停止时刻,传统傅里叶级数不能保证关节角速度和角加速度为零,使机器人无法平滑运行。
对于n阶非齐次方程组YNφ=τN,当由N组观测数据构成的观测矩阵YN和N组测量得到的输出力矩τN各有扰动δYN和δτN时,则添加扰动后的非齐次方程组为
(YN+δYN)(φ+δφ)=(τN+δτN)
(7)
由此解得
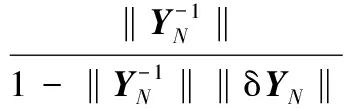
(8)
因YNφ=τN,则有‖τN‖≤‖YN‖‖φ‖,则式(8)可转化为
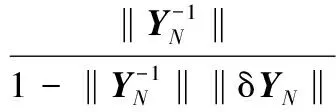
(9)
则动力学参数φ解的相对误差为
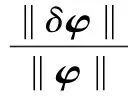
(10)


(11)

2.1改进的傅里叶级数
传统的M阶傅里叶级数定义如下:
(12)
式中,i为第i个关节;ωf为傅里叶级数的基频,每个关节的基频相同;ai,k、bi,k为傅里叶级数的系数;θ0i为偏移量;M为傅里叶级数的阶数,决定轨迹的带宽;ai,k、bi,k、θ0i为自由系数。
相应的关节运行速度和加速度为
(13)
机器人动力学参数辨识过程中,为保证运行的连续周期性,以及起始和结束时刻的平稳性,需要激励轨迹满足如下约束条件:
(14)
t0=0ttf=2π/(2πωf)
式中,t0、ttf分别为周期运动的起始和结束时刻;θi_init为第i关节的起始和结束时刻角度。
传统的傅里叶级数难以保证上述约束条件,因此,对传统傅里叶级数的激励轨迹进行改进,将常数项θ0i用5次多项式来代替,得到改进傅里叶级数的激励轨迹:

(15)
解得5次多项式的系数为

2.2激励轨迹优化

确定激励轨迹的形式之后,以一定频率对改进傅里叶级数进行采样,得到对应的关节角度、角速度和角加速度,共采集N组数据,从而构造观测矩阵YN。以观测矩阵YN的条件数作为目标函数,即适应度函数,为增强全局寻优能力,采用基于排挤机制的小生境遗传算法对傅里叶级数的系数进行优化,获得最小条件数时对应的系数ai,k、bi,k。
基于排挤机制的小生境遗传算法寻优步骤如下:
(1)选择编码策略。取M=5,改进的傅里叶级数共有20个待优化参数,因此,将20个参数进行实数编码,构成可行解的集合。
(2)确定适应度函数。根据式(6)计算得到观测矩阵YN,并以其条件数作为目标函数,即适应度函数。
(3)建立排挤机制。记第i个个体为pi,第j个个体为pj,则个体pi和pj之间的欧氏距离为‖pi-pj‖,取一较小整数ξ,f(·)表示个体的适应度值。在对每一代进行选择、交叉、变异操作之前,比较种群中任意两个个体的相似性,若‖pi-pj‖lt;ξ,则表明pi和pj的相似程度较大。通过对适应度较小者施加一较强的惩罚函数,使其适应度变得极小,从而排挤掉其中适应度较小者,即若f(pi)gt;f(pj),则令f(pi)=δf(pj)(δ为一很小的正数),则在以后的进化中pj会以极大的概率被淘汰掉。
(4)确定遗传算法参数。共进化400代,设置种群规模为50,交叉概率为0.4,变异概率为0.1。
(5)选择操作。种群中个体的选择操作采用轮盘赌法,并且将种群中个体适应度值取倒数,使得在轮盘中适应度值越小的个体在轮盘中被选中的概率越大。选择操作控制进化方向,使得下一代种群优于上一代种群。
(6)交叉操作。以一定概率对种群中的个体进行染色体交叉操作,被选中染色体的交叉位置相同。
(7)变异操作。对种群中染色体以一定概率进行变异操作,得到新的种群个体。
(8)判断是否已完成预定的进化代数,达到则停止进化。
采用改进的傅里叶级数作为激励轨迹,并用对改进傅里叶级数的20个参数进行寻优,优化得到的傅里叶级数参数如表1所示。观测矩阵YN的条件数随进化代数的变化过程如图1所示。
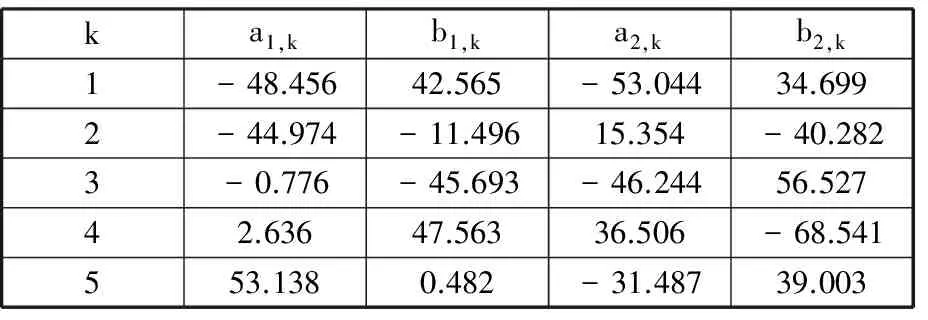
表1 优化后的傅里叶级数参数

图1 观测矩阵条件数Fig.1 Condition number of the observation matrix
得到的SCARA机器人两关节位置输入如图2所示,对应的两关节角速度和角加速度分别如图3、图4所示。从图中可以看出,各关节的起始和结束时刻位置相同,保证了轨迹运行的周期性,并且起始和结束时刻的关节角速度和角加速度为零,保证了机器人平滑运行。
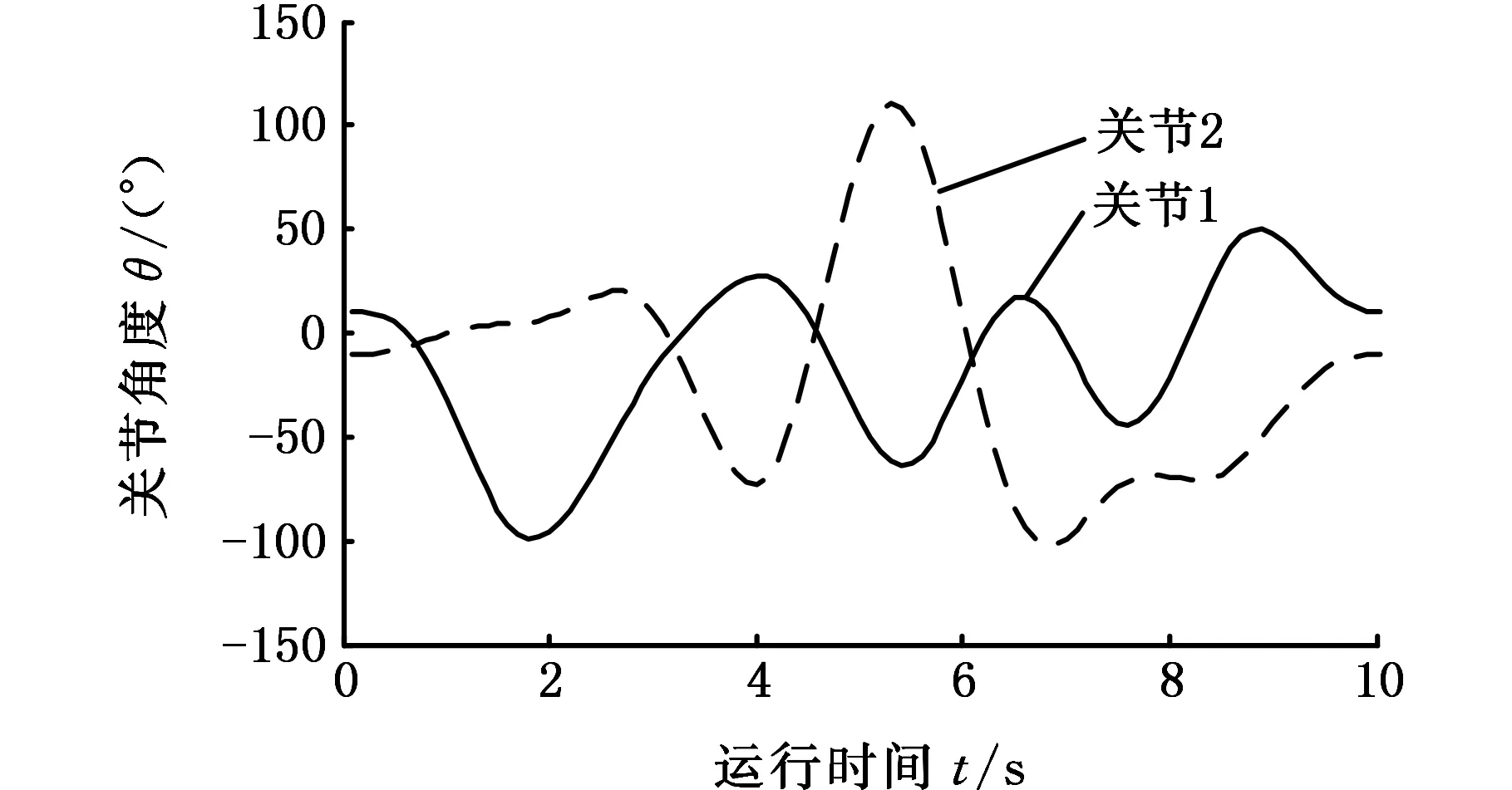
图2 激励轨迹角度Fig.2 Angle of the excitation trajectory

图3 激励轨迹角速度Fig.3 Angular velocity of the excitation trajectory

图4 激励轨迹角加速度Fig.4 Angular acceleration of the excitation trajectory
3 采样数据处理与参数估计
3.1采样数据处理
采用优化后的改进傅里叶级数作为机器人各关节激励轨迹,运行时对关节的输入力矩、关节角度和角速度进行采样。由于采样得到的数据易受测量噪声的影响,所以多次重复执行激励轨迹,对采样得到的关节角度、角速度和关节力矩取均值以提高信噪比:


为避免速度测量噪声给加速度计算带来的影响,文献[9]根据采样得到的各关节角度,反向拟合成傅里叶级数形式,再微分得到各关节角速度和角加速度。目前伺服电机一般采用高精度编码器,根据关节角度求角速度也经过滤波处理,得到的角速度信号比较准确,所以本文仅将采样得到的关节角速度拟合成傅里叶级数形式,关节速度的傅里叶级数

采用线性最小二乘法得到参数ai,k、bi,k,再对关节速度的傅里叶级数进行微分,得到关节角加速度信号,避免了两次微分带来的传递误差。
3.2加权最小二乘估计
机器人在重复跟踪激励轨迹时,在N个时间节点t1,t2,…,tN,通过高精度光电编码器对机器人关节角度和角速度进行采集,由于电机输出力矩不易直接测量,所以根据电机反馈输入电流和电机转矩系数计算得到关节输入力矩。最终得到式(5)中的观测矩阵YN和关节力矩向量τN。
式(5)的求解可采用加权最小二乘法[16]。在数据的采样中,关节角度和角速度是通过高分辨率的光电编码器经过滤波处理后测得的,相比关节力矩的测量噪声可以忽略不计。由力矩测量噪声的方差构成加权矩阵,从而区分准确数据和不准确数据,以此进一步提高辨识精度。此时,动力学参数φ的加权最小二乘估计
(16)

力矩测量噪声方差通过下式进行估算:
式中,Ν为一个周期内采样的点数;τij(k)为第j周期内,第i关节在第k次采样得到的力矩输出。
4 实验设计与结果分析
辨识实验在4自由度SCARA机器人的前两关节进行,如图5所示。机器人各个关节采用永磁同步伺服电机驱动,关节位置通过伺服电机的17位光电编码器测量,速度通过对位置信号滤波后计算得到,力矩信号通过伺服电机的电枢反馈电流Iq和电机转矩系数计算得到。机器人各个关节由伺服驱动器进行独立PID控制,在NI实时系统上通过NI板卡进行激励轨迹的位置给定。

图5 SCARA机器人前两关节Fig.5 The first two joints of SCARA robot
改进的激励轨迹为5阶傅里叶级数,即M=5,则两个关节共有20个参数需要进行优化,优化后的关节激励轨迹角度、角速度和角加速度分别如图2、图3和图4所示。傅里叶级数基频ωf=0.1 Hz,轨迹周期为10 s,重复执行激励轨迹周期数L=5。
采用文献[9]中提出的方法和本文提出的方法分别进行辨识,得到辨识结果如表2所示。

表2 辨识结果
机器人动力学参数的实际值是无法提前测得的,不能将两种方法辨识得到的值与实际值进行对比。所以,选取一条不同于激励轨迹的可执行轨迹作为验证轨迹,使机器人跟踪验证轨迹,同时对关节输入力矩信号进行采样,再根据辨识出的动力学参数φ和期望的运动轨迹,用式(3)计算出关节力矩的预测值。为评价参数辨识的精度,采用力矩测量值和预测值的残差均方根εRMS作为评价指标:

式中,τm(k)、τpred(k)分别为跟踪验证轨迹时,第k个采样点处的采样力矩和力矩预测值;K为每次运行的采样点总数。
为满足速度和加速度的边界条件,仍选取式(15)所示形式的轨迹作为验证轨迹,如图6所示。

图6 SCARA机器人关节验证轨迹Fig.6 The joint validation trajectory of the SCARA robot
将上述验证轨迹作为机器人两关节的位置给定,根据两种方法辨识得到的动力学参数,计算得到相应的各关节预测力矩输出。同时采集各个关节的实际输出力矩,得到两关节测量力矩和预测力矩如图7所示。
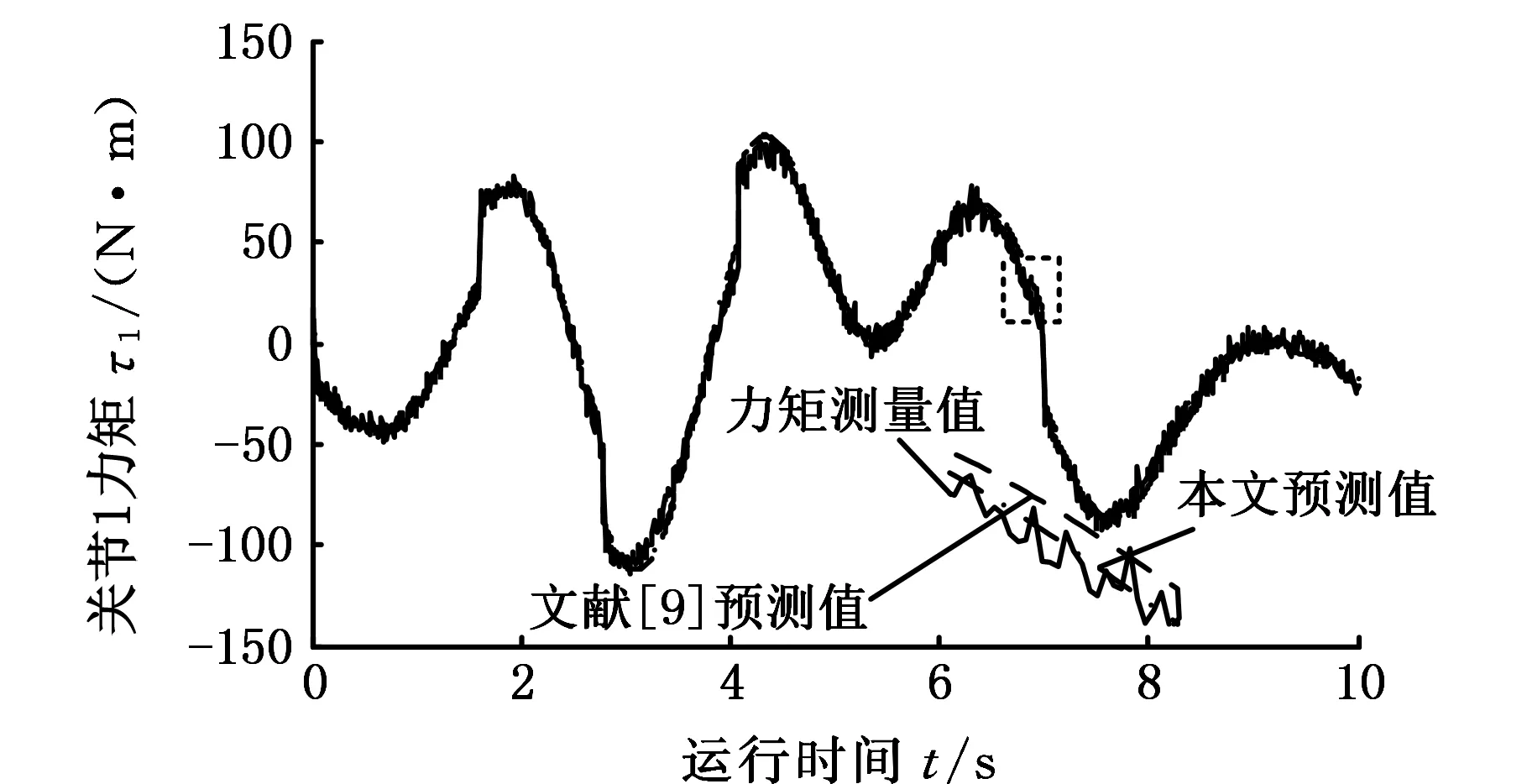
(a)关节1

(b)关节2图7 关节力矩测量值和预测值Fig.7 The measured values and predicted values ofthe joint torque
根据式(16)计算得到两种方法对应的各关节力矩残差均方根,如表3所示。可以看出:对傅里叶级数进行改进,使得角速度和角加速度在轨迹起始和停止时刻为零,并且使用基于排挤机制的小生境遗传算法优化观测矩阵条件数的方法,可以明显提高辨识精度。采用所提方法,两关节力矩测量值和预测值的残差均方根分别降低了11.50%和26.35%。

表3 两关节力矩残差均方根
5 结论
根据SCARA机器人的完整动力学方程,推导得到动力学模型的线性形式。采用改进的傅里叶级数作为机器人关节的激励轨迹,使得关节角度满足连续周期性,并且关节角速度和角加速度在轨迹起始和停止时刻为零。为提高辨识精度,采用基于排挤机制的小生境遗传算法对激励轨迹的系数进行优化,以最小化SCARA机器人观测矩阵的条件数。考虑到测量噪声的影响,采用加权最小二乘法(WLS)作为参数估计方法。实验结果表明,采用所提方法能准确辨识出SCARA机器人的动力学参数,并且相比于文献[9],两关节力矩测量值和预测值的残差均方根分别降低了11.50%和26.35%。
[1] 王田苗, 陶永. 我国工业机器人技术现状与产业化发展战略 [J]. 机械工程学报, 2014, 50(9): 1-13.
WANG Tianmiao, TAO Yong. Research Status and Industrialization Development Strategy of Chinese Industrial Robot [J]. Journal of Mechanical Engineering, 2014, 50(9): 1-13.
[2] BROGARDH T. Robot Control Overview: an Industrial Perspective [J]. Modeling Identification and Control, 2009, 30(3): 167-180.
[3] WU J, WANG J, YOU Z. An Overview of Dynamic Parameter Identification of Robots [J]. Robotics and Computer-Integrated Manufacturing, 2010, 26(5): 414-419.
[4] BONA B, INDRI M, SMALDONE N. Rapid Prototyping of a Model-based Control with Friction Compensation for a Direct-drive Robot [J]. IEEE/ASME Transactions on Mechatronics, 2006, 11(5): 576-584.
[5] 耿令波. 工业机器人动力学参数辨识方法研究 [D]. 南京:南京航空航天大学, 2013.
GENG Lingbo. Study on Method of Dynamic Parameter Identification of Industrial Robots [D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2013.
[6] BENIMELI F, MATA V, VALERO F. A Comparison between Direct and Indirect Dynamic Parameter Identification Methods in Industrial Robots [J]. Robotica, 2006, 24(5): 579-590.
[7] QIN Z, BARON L, BIRGLEN L. A New Approach to the Dynamic Parameter Identification of Robotic Manipulators [J]. Robotica, 2010, 28(4): 539-547.
[8] ATKESON C G, AN C H, HOLLERBACH J M. Estimation of Inertial Parameters of Manipulator Loads and Links [J]. International Journal of Robotics Research, 1986, 5(3): 101-119.
[10] 黎柏春, 王振宇, DEMIN A,等. 一种改进的机器人动力学参数辨识方法 [J]. 中国工程机械学报, 2015, 13(5): 381-387.
LI Baichun, WANG Zhenyu,DEMIN A, et al. Improved Parametric Identification Method Based on Robot Dynamics [J]. Chinese Journal of Construction Machinery, 2015, 13(5): 381-387.
[11] 丁亚东, 陈柏, 吴洪涛,等. 一种工业机器人动力学参数的辨识方法 [J]. 华南理工大学学报: 自然科学版, 2015, 43(3): 49-56.
DING Yadong, CHEN Bai, WU Hongtao, et al. An Identification Method of Industrial Robot’s Dynamic Parameters [J]. Journal of South China University of Technology (Natural Science Edition), 2015,43(3): 49-56.
[12] 陈恩伟, 刘正士, 干方建. 机器人末端臂惯性参数辨识的人工神经网络方法 [J]. 中国机械工程, 2006, 17(3): 268-271.
CHEN Enwei, LIU Zhengshi, GAN Fangjian. Application of ANN Method in Inertial Parameter Identification of the End Effector of Robot [J]. China Mechanical Engineering, 2006, 17(3): 268-271.
[13] 蔡自兴.机器人学[M].北京:清华大学出版社,2005: 87-94.
CAI Zixing. Robotics [M]. Beijing:Tsinghua University Press, 2005: 87-94.
[14] 陆金伟, 李跃民. SCARA机器人的完整动力学显方程的推导[J]. 振动、测试与诊断, 1995(3): 23-29.
LU Jinwei, LI Yuemin. The Derivation of the Complete Dynamic Equation of the SCARA Robot [J]. Journal of Vibration and Measurement and Diagnosis, 1995(3): 23-29.
[15] LIN S K. Minimal Linear Combinations of the Inertia Parameters of a Manipulator [J]. IEEE Transactions on Robotics and Automation, 1995, 11(3): 360-373.
[16] CALANCA A, CAPISANI L M, FERRARA A, et al. MIMO Closed Loop Identification of an Industrial Robot [J]. IEEETransactions on Control Systems Technology, 2011, 19(5): 1214-1224.
(编辑王旻玥)
AnImprovedDynamicsParameterIdentificationMethodforSCARARobots
YAN Hao1BAI Ruilin1JI Feng2
1.Key Laboratory of Advanced Process Control for Light Industry,Jiangnan University,Wuxi,Jiangsu,214122 2.Xinjie Electronic Co.,Ltd.,Wuxi,Jiangsu,214072
In order to identify the dynamics parameters of SCARA robots, a new identification method was proposed based on improved Fourier series. According to the complete dynamics equations of the SCARA robots, a linear form of the dynamics model was derived. The improved Fourier series was used as the excitation trajectory of the robot joints, and the joint angles satisfied the continuous periodicity, and the angular velocities and angular accelerations were as zero at the beginning and end of the trajectory. In order to further improve the identification accuracy, the condition numbers of the observation matrix of the SCARA robots were used as the objective function, and based on crowding mechanism the niche genetic algorithm was used to optimize the coefficients of the trajectory. Considering the influences of measurement noises, the weighted least square method (WLS) was used as the parameter estimation method. The experimental results show that the proposed method may accurately identify the dynamics parameters of the SCARA robots, torque measurements and predictive values of two joints, the residual root mean square values are reduced by 11.50% and 26.35% respectively.
robot; dynamics; niche genetic algorithm; excitation trajectory; parameter identification
TP242
10.3969/j.issn.1004-132X.2017.22.010
2016-12-08
江苏省产学研前瞻性联合研究项目(BY2015019-38);江苏高校优势学科建设工程项目(PAPD)
严浩,男,1992年生。江南大学物联网工程学院硕士研究生。主要研究方向为检测技术与自动化装置、机器人控制技术。E-mail:jiangnan_yh@163.com。白瑞林,男,1955年生。江南大学物联网工程学院教授、博士研究生导师。吉峰,男,1981年生。无锡信捷电气股份有限公司工程师。
