基于数据/极值联合对称延拓的端点效应处理及其应用

吴 琛， 项 洪， 杜喜朋

(1.福建工程学院 土木工程学院，福州 350118; 2.福建省土木工程新技术与信息化重点实验室，福州 350118)

基于数据/极值联合对称延拓的端点效应处理及其应用

吴 琛1,2， 项 洪1,2， 杜喜朋1,2

(1.福建工程学院 土木工程学院，福州 350118; 2.福建省土木工程新技术与信息化重点实验室，福州 350118)

Hilbert-Huang变换在EMD分解中因端点非极值点，无法满足样条插值的要求导致包络线异常，产生端点飞翼；在Hilbert变换中又因卷积计算和Fourier变换能量泄露的原因，也使端点产生飞翼。提出数据/极值联合对称延拓的方法，通过端部数据对称延拓，把EMD分解和Hilbert变换过程中产生的端点效应释放到数据外端，一举解决两阶段的端点飞翼问题；通过极值点对称延拓进一步控制三次样条包络曲线的走势，使原始数据的包络曲线更加准确。经仿真信号验证，联合对称延拓的方法具有良好的抑制效果。当该方法应用于结构动力响应非线性特征分析时，不仅具有明确的物理意义，而且能较准确地表征结构进入非线性状态时出现“频带扩展”和“主导频率飘移”的力学特征。

Hilbert-Huang变换; 端部数据; 极值点; 对称延拓; 非线性力学特征

Hilbert-Huang变换(Hilbert-Huang Transforms, HHT)是由Huang等[1]于1998年在经典的Hilbert变换基础上提出的一种非平稳信号处理技术。该方法由经验模态分解(Empirical Mode Decomposition, EMD)与Hilbert谱分析(Hilbert Spectral Analysis, HSA)两部分组成，不仅赋予了瞬时频率合理的定义、物理意义和求解方法，而且不需要先验基底，可依据数据本身的时间尺度特征进行模态分解，具有很强的局部自适应性。目前，该方法已广泛地应用于地震信号及响应研究[2]、系统识别[3]、生物医学[4]、故障诊断[5]、噪声处理[6]、图像处理[7]等各个领域。但是，由于HHT建立在经验筛分的基础上，必然存在一些固有的问题亟待改进。除筛分终止条件、模态混叠、包络线和均值曲线的拟合外，端点飞翼的抑制是使HHT分析结果具有有效性的一项重要工作[8]。

根据端点处理的原理，端点效应抑制的方法大致可分为三类：①极值延拓，如极值点对称延拓[9]、相似极值延拓[10]、极值平移延拓[11]、多项式拟合延拓[12]等，这类方法不延拓信号本身数据点，仅以端点附近极值点的特性决定延拓极值，这对于宽频带、非平稳的复杂信号而言，显然不能准确反应信号的真实趋势。②波形延拓，即通过在信号两端增加波形数据的方式进行端点延拓，其中最为典型的是由Huang等提出并在美国申请了专利的特征波法[13]和由黄大吉教授提出的波形镜像延拓法[14]。前者对于不同特征尺度的信号在不同的端点位置所添加的特征波也应不同，因此正如Huang等曾经指出的，EMD所面临的边界延拓问题仍未得到很好的解决；后者虽具有良好的抑制效果，但由于镜像延拓后得到的极值点数量是原来的2倍，因而计算用时大大增加。③数据预测延拓法，如神经网络预测[15]、自回归模型预测[16]和支持向量回归机法等[17]，这些方法有的仅适用于平稳或简单非平稳信号，有的由于复杂的模型和不定性的参数和较长的运算时间，限制了其应用范围，有的需要在EMD分解和Hilbert变换两阶段分别进行端点处理，工作量较大。因此，HHT的端点效应仍然是近十年来专家学者们重点关注和研究的问题。本文将提出一种计算简单、高效，计算精度良好的端点抑制方法，并通过仿真信号和结构响应非线性力学行为的工程实例验证其抑制效果。

大部分结构在强震作用下将会表现出非线性的力学行为，这恰是结构产生破坏的前兆，因此探究结构进入非线性的特征具有重要的意义[18]。非线性体系动力响应频谱成分的时变特性是体系非线性力学行为的重要特征。由于Fourier变换全局意义上的传递函数不能很好地描述这种时变特征，小波变换也存在着类似于Fourier变换的伪谐波分量，因此采用HHT时频分析方法进行结构响应非线性特征分析不失为一种好方法。但在这一研究中，如不能对HHT的端点效应进行良好处理，将直接影响到分析的正确性。本文将采用联合对称延拓的方法进行结构地震响应的非线性力学行为分析。

1 HHT端点效应

HHT的端点效应在EMD和Hilbert变换中都存在，两种失真的叠加造成了HHT无法正确反应信号所包含的信息，影响了分析结果的有效性。

1.1 EMD分解的端点效应

在EMD分解中，需要对数据序列的极值点进行三次样条插值，获得信号的上、下包络线。由于三次样条插值要求具有光滑的一次微分和连续的二次微分，但对于有限长度的数据序列而言，信号的两个端点不一定是极值点，无法提供样条插值函数所需要条件，也无法根据端点附近的信息获得端点外侧的信息，这必然导致拟合包络线在信号两端发生偏离实际包络线趋势的现象。并且，随着“筛分”的进行，发散现象将逐渐由数据两端向内部“污染”。因此，对于短数据信号以及极值点之间时间跨度较大的低频分量而言，端点飞翼尤为明显。

1.2 Hilbert变换的端点效应

(1)

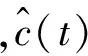
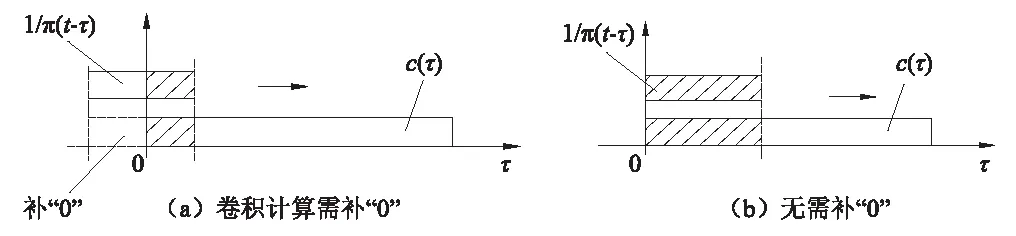
图1 卷积示意图Fig.1 Convolution schematic

此外，Hilbert变换的快速算法是基于Fourier变换实现的，在端点处容易引起能量泄露，也会造成信号的失真。

1.3 端点效应抑制效果评价指标

仿真信号通常可通过HHT结果与理论曲线的比较来检验端点效应的抑制效果，而对工程实际中的复杂信号，获得理论曲线作为评价参照是困难的。因此，需要通过一定评价指标加以验证端点抑制的有效性。

首先，为避免端点效应引起信号包络线畸变、产生虚假成分致使信号总能量增加，可通过比较EMD分解前后的能量来评估端点效应的程度。定义采样步数为m的信号S(t)的有效能量为

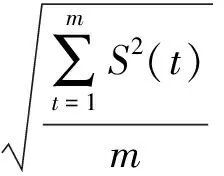
(2)

则分解前后的能量比为

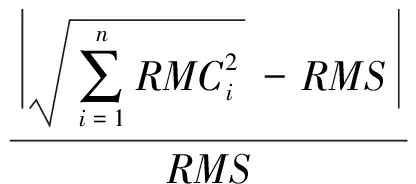
(3)

式中：n为IMF分量总数；RMCi为IMF分量ci的有效能量，可依式(2)计算。能量比θ越小说明虚假成份越少。

其次，由于信号S(t)的分解特性受到端点效应的影响，因此可通过各IMF分量c(t)之间的局部正交性指标IO判别端点处理的效果

(4)

该指标越小说明正交性越好。

再次，端点抑制算法的运行时间t也是一个重要的衡量指标，用时越长，算法越复杂，计算的成本越高。

2 数据/极值联合对称延拓

2.1 改进思路

根据端点效应产生的原因，提出如下改进思路：

(1) 为避免数据迅速受到端点效应的“污染”、缓解Hilbert变换卷积计算中的“褶皱”现象，可通过端点附近的数据延拓，增加信号长度，并使Hilbert变换卷积“褶皱”外延，实现EMD分解和Hilbert变换两阶段端点效应的抑制。延拓的数据应能反映端部数据的自然趋势，如采用端部数据对称延拓，既能使延拓后的波形反映出原信号在端点处的变化趋势，又能体现原信号已知极值点的信息。又由于三次样条插值时需要用到前后各两个临近点。因此，每端延拓的数据长度应含盖两个极大值点和两个极小值点。

(2) 数据序列的端点很可能不是极值点, 若将它作为对称点，当端点与其相邻极值相差较小时，包络线如图2所示，在端点处突然收缩产生畸形，因此需要判别端点是否为对称点。

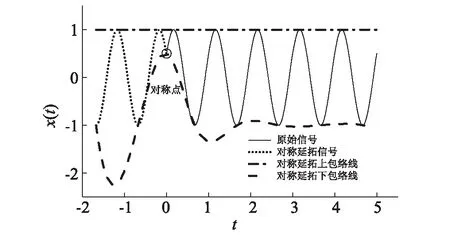
图2 包络线在端点处畸变Fig.2 Envelopes distortion at the endpoint

(3) 如图3所示，对数据序列较短或信号频率较低的情况，当端点值与相邻极值相差较大时，如直接取端部数据延拓后的端点作为极值点，延拓部分的包络线将不能完整包络所有信号，并影响到原始信号包络曲线的准确性。为进一步控制数据延拓后的包络线走向，并考虑到上、下包络是分别由极大值和极小值连接而成的，因此可仅对极大值和极小值进行进一步对称延拓，以获得较为准确的包络线参与EMD筛分。

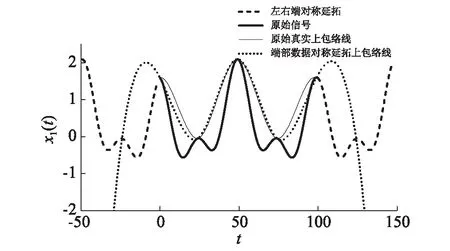
图3 端部数据对称延拓Fig.3 Symmetrical extension of the end data

基于以上改进思路，本文提出数据/极值联合对称延拓的方法实现HHT的端点抑制。

2.2 技术要点

数据/极值联合对称延拓法旨在通过EMD筛分之前的端部数据对称延拓，把EMD分解和Hilbert变换过程中产生的端点飞翼释放到数据外端，一举解决两阶段的端点效应，后续计算无需再对端点进行处理；通过极值点对称延拓进一步控制三次样条包络曲线的走势，避免首次延拓的信号落到包络线之外，影响到原始数据的内部。该方法的技术要点如下：

(1) 端部数据对称延拓。

设原始信号x(t)的端点为x(0)，极大值为U(1)，U(2)，…，U(n)，极小值为L(1)，L(2)，…，L(m)。以信号左端为例，当x(0)≥U(1)或x(0)≤L(1)时(见图4(a)和图4(b))，以x(0)为对称点进行数据延拓；当L(1)lt;x(0)lt;U(1)时(见图4(c)和图4(d))，以与x(0)相邻的极值点为对称点进行数据延拓。对称延拓的数据范围含盖了极大值点U(1)，U(2)和极小值点L(1)，L(2)。信号右端延拓方法与左端相同，经端部数据对称延拓后的信号记为x1(t)。

图4 左端数据对称延拓Fig.4 The left data symmetrical extension

(2) 极值点对称延拓。

记信号x1(t)的端点为x1(0)，端点极大值点为U1(1)，U1(2)，…，U1(n+4)，极小值为L1(1)，U1(2)，…，U1(m+4)。仍以信号左端为例，当x1(0)≥U1(1)或x1≤L1(1)时(见图5(a)和图5(b))，以为对称点对称延拓极大值点U1(1)、U1(2)和极小值点L1(1)、L1(2)；当L1(1)lt;x1(0)lt;U1(1)时(见图5(c)和图5(d))，以与相邻的极值点为对称点进行上述四个极值点的对称延拓。信号x1(t)右端的延拓方法同左端。

图5 左端极值点对称延拓Fig.5 The left extremum symmetrical continuation

(3) Hilbert-Huang变换。

按数据/极值联合对称延拓的结果进行三次样条插值，获得信号x1(t)的上下包络线，经EMD分解，截取原始信号x(t)时域范围内的IMF分量，并通过Hilbert变换可获得Hilbert幅值谱、能量谱、瞬时能谱等分析结果。其中，Hilbert能量谱能清晰地反映信号的能量在频域的分布情况。

3 仿真信号验证

为验证本文提出的数据/极值联合对称延拓法的有效性，现以一列仿真信号为例进行HHT端点处理和时频分析。已知信号

x(t)=cos(2πt/50)+60cos(2πt/25)+0.5cos(2πt/200)

3.1 EMD筛分结果的比较

图6为直接以端点为极值获得的IMF分量，图7为本文方法的筛分结果，二者分别与理论曲线进行了比较。对比两图可知，经数据/极值联合对称延拓后，不仅使各IMF分量端点附近的飞翼现象得到了良好的抑制，更避免了端点效应向信号内部的传递。可见，本文方法对处理EMD筛分过程中产生的端点飞翼具有良好的效果。

3.2 瞬时频率的比较

图8(a)和图8(b)分别为端点处理前后仿真信号的瞬时频率。如图可知，如直接以端点为极值点，Hilbert谱的两端飞翼现象严重。经数据/极值联合对称延拓后，Hilbert谱的频率分别集中在0.005 Hz, 0.02 Hz和0.04 Hz处，分别对应仿真信号的三个频率成分，可见本文方法对于Hilbert变换所产生端点飞翼也具有良好的抑制效果。

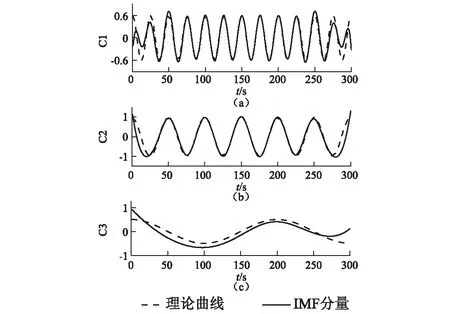
图6 未经端点处理的IMF分量与理论曲线的比较Fig.6 Comparison between the IMF components without endpoint processing and the theoretical curves

图7 联合对称延拓获得的IMF分量与理论曲线的比较Fig.7 Comparison between the IMF components with joint symmetrical extension and the theoretical curves

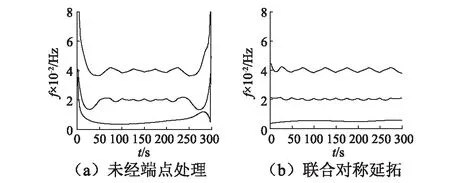
图8 仿真信号的瞬时频率对比Fig.8 Comparison of instantaneous frequency for the simulation

3.3 Hilbert能量谱的比较

为进一步对比仅采用极值点对称延拓、仅采用端部数据对称延拓以及联合对称延拓后端点效应的改善效果，现从Hilbert能量谱的角度展示三种方法对应的信号能量分布情况。如图9(a)、图9(b)所示，单一方法在原信号并不存在的0.01 Hz上分布了较高的能量，出现了模态混叠。经联合对称延拓后，如图9 (c)所示，Hilbert能量分别集中于仿真信号的三个主要频率成份，可见本文方法还具有避免模态混叠的效果。

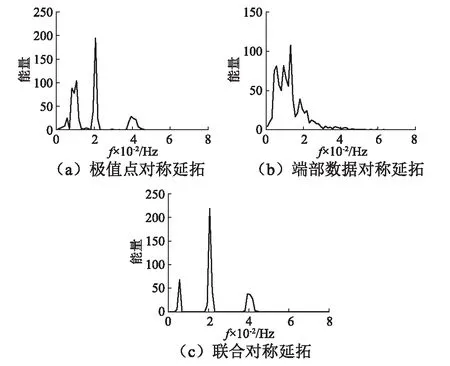
图9 仿真信号的Hilbert能量谱对比Fig.9 Comparison of Hilbert energy spectra for the simulation

3.4 评价指标的比较

为进一步评价端点处理的效果，能量比θ、IO值、用时t等评价指标，如表1所示。

表1 各种延拓方法评价指标

显然，任意一种端点处理方法均能达到抑制端点效应的目的。其中，联合对称延拓的能量一致性和局部正交性最优；计算用时方面，即使在普通计算机上运行也与其他方法不相上下；并且，该方法相对其他两种单一处理方法而言，具有一次延拓一举解决两阶段端点效应的优势，还可缓解模态混叠。

4 地震响应非线性特征分析

现进行单自由度体系在地震作用下的弹性时程分析和弹塑性时程分析，并通过HHT进行地震响应的非线性力学行为研究。为避免阻尼对分析结果的干扰，阻尼比不参与计算。

4.1 线性体系动力响应HHT分析

将峰值为200 gal、持时为30 s的Elcentro地震波输入基本频率为3.25 Hz的单自由度线性体系，经弹性时程分析得绝对加速度响应，如图10所示。该响应端点处理前后的EMD分解结果比较及Hilbert能量谱的比较，分别如图11和图12所示。

如图11(a)所示，未经端点处理时，C2～C6为端点效应引起的虚假模态分量，并导致了图12(a)Hilbert能量谱在0.16 Hz附近出现虚假主导频率。

经本文方法端点处理后，图11(b)中C1～C7均描述了线性体系动力响应的本征振动模态。其中，C1分量幅值最大，频率如图12(b)所示保持在以基本频率3.25 Hz为中心的窄小频带内，反映了线性体系自振特性对动力响应的影响，说明线性结构对输入信号具有滤波和放大的作用。而C2～C7则来源于非平稳地震动自身的波内调制(即一个IMF分量内频率随时间不断小幅变化)，其值微小至可忽略不计，说明地震动原有的波内调制在通过结构体系后即被相应地 “滤掉”。

图10 线性体系加速度响应Fig.10 Acceleration of linear system

图11 线性体系加速度响应EMD分解结果对比Fig.11 Comparison of EMD decomposition for acceleration of the linear system

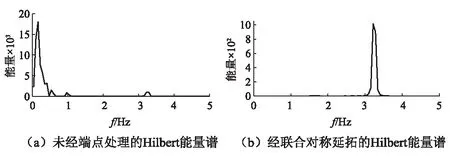
图12 线性体系加速度响应Hilbert能量谱对比Fig.12 Comparison of Hilbert energy spectra of linear system

4.2 非线性体系动力响应HHT分析

将峰值为400 gal、持时为30 s的Elcentro地震波输入基本自振周期为3.25 Hz的非线性体系，弹塑性时程分析采用三线性刚度退化模型，第一刚度折减系数为0.4，第二刚度折减系数为0.1。取开裂位移为1 mm，屈服位移为6 mm。经弹塑性时程分析的结构绝对加速度响应，如图13所示。

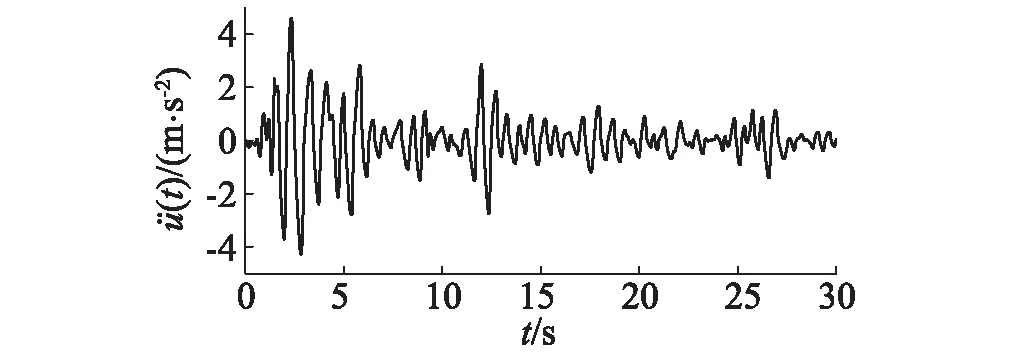
图13 非线性体系加速度响应Fig.13 Acceleration of non-linear system

从绝对加速度响应的EMD分解结果来看，图14(a)中C2～C6存在明显的端点发散，并导致图15(a)Hilbert能量谱在0.09 Hz处出现虚假主导频率。经本文方法处理后，图14(b)则表现为符合IMF两个基本特征的本征模态分量，对应的图15(b)Hilbert能量谱也更具合理性。

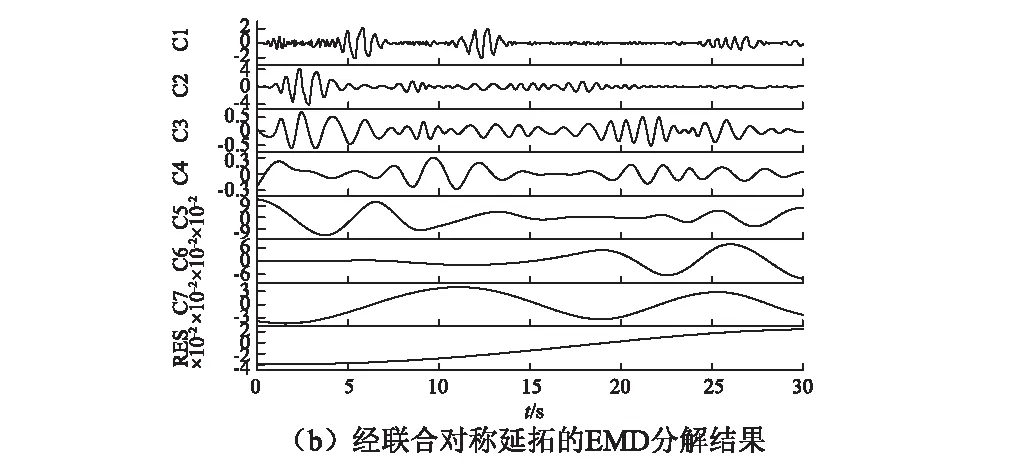
图14 非线性体系加速度响应EMD分解结果对比Fig.14 Comparison of EMD decomposition for acceleration of the non-linear system

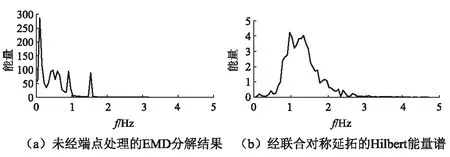
图15 非线性体系加速度响应Hilbert能量谱对比Fig.15 Comparison of Hilbert energy spectrum of non-linear system

由于各IMF分量的幅值和频率都随时间不停变化着，说明体系的加速度响应是若干IMF分量波间组合与各IMF分量波内调节共同作用的结果。这种波内调制或来自于输入的地震动，或来源于结构的阻尼特性，或来自于体系屈服与卸载的非线性力学行为。如“4.1”所述，地震动的波内调制可被体系相应滤掉，又因本算例不计阻尼，不存在阻尼使频带扩展的可能性。因此，体系的非线性是造成加速度时程蕴含波内调制的主要原因，非线性体系Hilbert能量谱也正由于这种波内调节机制形成了分布离散的宽频带，如图15(b)所示。这一宽频带的产生具有明确的物理意义：它是非线性体系在地震动输入下非线性力学行为的标志。

并且，主导频率并非结构的基本自振频率，而是向低频方向飘移，如图15(b)所示。这是由于非线性体系同时受初始频率、开裂频率和屈服频率的影响，因此其主导频率并不对应结构基本频率，而有向着开裂频率和屈服频率靠近的趋势。这是动力响应非线性特征的又一个标志。

5 结 论

本文分析了EMD分解与Hilbert变换两阶段产生端点飞翼的原因，提出基于数据/极值联合对称延拓的改进思路，给出改进的技术要点。经仿真信号和实际地震响应非线性力学特征的分析，得到如下结论：

(1) 端部数据对称延拓可避免信号数据迅速受到端点效应的“污染”，并缓解Hilbert变换卷积计算中的“褶皱”现象；数据延拓对称点的判别可避免包络线在端点处突然收缩，产生畸形；端部数据对称延拓后再对称延拓极值点可进一步调整包络线走势，使其更加接近理想曲线。

(2) 仿真信号的验证算例表明，经数据/极值联合对称延拓后，EMD分解和Hilbert变换两阶段的端点飞翼现象均得到了良好的抑制。与极值点对称延拓、端部数据对称延拓等单一处理方法相比，本文方法在计算用时相当的前提下，端点处理效果更佳，还可减小模态混叠、改善局部正交性、所获得的Hilbert能量更为集中。并且，该方法简单易实施，只需在EMD分解之前一次延拓，在随后的Hilbert变换中无需再进行端点处理。

(3) 实际地震动响应的HHT分析表明，数据/极值联合对称延拓法可抑制由于端点飞翼产生的多余虚假能量。由该方法所产生的良好端点效应抑制效果是进行结构动力响应非线性力学特征分析的必备前提。倘若端点效应使HHT结果失真，则后续的非线性力学特征分析将失去意义。

(4) 经端点效应处理后的HHT以蕴涵在结构动力响应本征振动模态中的波内调节机制来描述体系非线性力学行为。这种波内调节机制将使相应的IMF的瞬时频率产生波动，并必然导致体系动力响应的Hilbert能量谱中出现“频带展宽”和“主导频率飘移”的现象。

[ 1 ] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proc.R.Soc.Lond., 1998, 454: 903-995.

[ 2 ] 吴祚菊,张建经,王志佳,等.改进HHT算法在地震动特性分析中的应用研究[J].地震工程与工程振动, 2015,35(2): 86-93.

WU Zuoju, ZHANG Jianjing, WANG Zhijia, et al. Research on seismic instantaneous frequency characteristics based on modified HHT algorithm [J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(2): 86-93.

[ 3 ] 韩建平,李林,王洪涛, 等. 基于Hilbert-Huang变换和随机减量技术的模态参数识别[J]. 世界地震工程,2011, 27(1): 72-77.

HAN Jianping, LI Lin, WANG Hongtao, et al. Modal parameter identification based on Hilbert-Huang transform and random decrement technique [J]. World Earthquake Engineering, 2011, 27(1): 72-77.

[ 4 ] TSENG Yili, KO Pinyu, JAW Fushan. Detection of the third and fourth heart sounds using Hilbert-Huang transform[J]. BioMedical Engineering Online, 2012,11(1): 1-8.

[ 5 ] LEI Yaguo, LIN Jing, HE Zhengjia, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery [J]. Mechanical Systems and Signal Processing, 2013, 35(1/2): 108-126.

[ 6 ] 杨光亮,朱元清,于海英.基于HHT的地震信号自动去噪方法[J]. 大地测量与地球动力学,2010,30(3): 39-42

YANG Guangliang, ZHU Yuanqing, YU Haiying.Automatic de-nosing algorithm of earthquake signal based on HHT decomposition[J].Journal of Geodesy and Geodynamics, 2010,30(3): 39-42.

[ 7 ] IOANNIDIS K, ANDREADIS I. A digital image stabilization method based on the Hilbert-Huang transform [J]. IEEE Transaction on Instrumentation and Measurement, 2012,61(9): 2446-2457.

[ 8 ] HUANG N E, WU M, LONG S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis [J]. Proc.R.Soc.Lind.,2003, 459: 2317-2345.

[ 9 ] 舒忠平, 杨智春.抑制经验模分解边缘效应的极值点对称延拓法[J]. 西北工业大学学报,2006,24(5): 639-643.

SHU Zhongping , YANG Zhichun. A better method for effectively suppressing end effect of empirical mode decomposition (EMD)[J]. Journal of Northwestern Polytechnical University, 2006, 24(5): 639-643.

[10] 沈路,周晓军,张志刚,等.Hilbert-Huang变换中的一种端点延拓方法[J].振动与冲击,2009,28(8): 168-171.

SHEN Lu, ZHOU Xiaojun, ZHANG Zhigang, et al. Boundary- extension method in Hilbert-Huang transform[J].Journal of Vibration and Shock, 2009,28(8): 168-171.

[11] 王学敏,黄方林. EMD端点效应抑制的一种实用方法[J]. 振动、测试与诊断， 2012，32(3): 493-497.

WANG Xuemin, HUANG Fanglin. Practical method to restrain the end effect of EMD [J]. Journal of Vibration, Measurement amp; Diagnosis, 2012,32(3): 493-497.

[12] 刘慧婷,张旻,程家兴. 基于多项式拟合算法的EMD端点问题的处理[J].计算机工程与应用, 2004, 40(16): 84-86.

LIU Huiting, ZHANG Min, CHENG Jiaxing. Dealing with the end Iusse of EMD based on polynomial fitting algorithm [J]. Computer Engineering and Applications, 2004, 40(16): 84-86.

[13] HUANG N E. Empirical mode decomposition apparatus, method and article of manufacture for analysing biological signals and performing curve fitting: US 6381559[P].2002-02-04.

[14] 黄大吉,赵进平,苏纪兰. 希尔伯特-黄变换的端点延拓[J]. 海洋学报, 2003,25(1): 1-11.

HUANG Daji, ZHAO Jinping, SU Jilan. Practical implementation of Hilbert-Huang transform algorithm [J]. Acta. Oceanologica Sinica, 2003,25(1): 1-11.

[15] 邓拥军,王伟,钱成春,等. EMD方法及Hilbert 变换中边界问题的处理[ J].科学通报, 2001, 46(3): 257-263.

DENG Yongjun, WANG Wei, QIAN Chengchun, et al. Management of boundary problem in EMD and HHT [ J]. Chinese Science Bulletin, 2001, 46( 3): 257-263.

[16] 窦东阳,赵英凯.利用ARIM A改进HHT端点效应的方法[J].振动、测试与诊断, 2010, 30( 3): 249-253.

DOU Dongyang, ZHAO Yingkai. Method of improving ending effect of Hilbert-Huang transform using autoregressive integrated moving average model [J]. Journal of Vibration, Measurement amp; Diagnosis, 2010, 30(3): 249-253.

[17] 李雪耀,张汝波,王武.基于支持向量回归机的HHT边界效应处理[J].智能系统学报,2007,2(3): 39-44.

LI Xueyao, ZHANG Rubo, WANG Wu. End effects processing in HHT based on support vector regression machines [J]. CAAI Transaction on Intelligent Systems, 2007,2(3): 39-44.

[18] 吴琛,周瑞忠. 基于Hilbert谱的结构动力响应非线性特征分析[J].振动与冲击,2013,32(14): 70-76.

WU Chen, ZHOU Ruizhong. Nonlinear behavior analysis of structural dynamic response based on Hilbert spectrum [J]. Journal of Vibration and Shock,2013,32(14): 70-76.

AprocessmethodforendeffectsofHHTbasedondata/extremasymmetricalextensionanditsapplication

WUChen1,2,XIANGHong1,2,DUXipeng1,2

(1.SchoolofCivilEngineering,FujianUniversityofTechnology,Fuzhou350118,China;2.FujianProvincialKeyLaboratoryofAdvancedTechnologyandInformatizationinCivilEngineering,Fuzhou350118,China)

End effects appear in EMD decomposition because an end point is not an extreme point and the requirements of spline interpolation can not be met. End effects are produced in Hilbert transform due to the convolution calculation and the energy leakage of Fourier transform. In this paper, a data/ extrema symmetrical extension method was proposed to solve the problem. Using end data symmetrical extension, the end swings resulted from EMD and Hilbert transform could be released to the outside of the data. Through extrema symmetrical extension, the shape of the cubic spline envelope curve was further controlled and the envelope curve of the original data was more accurate. The simulation demonstrates the effectiveness of the method. When this method is applied to the structural dynamic non-linear characteristics analysis, clear physical meaning and two non-linear mechanical characteristics including "frequency band extension" and "main frequency drift" can be described accurately.

Hilbert-Huang transforms; end data; extrema; symmetrical extension; non-linear mechanical characteristics

国家自然科学基金项目(51108083)；福建省自然科学基金项目(2015J01631)；福建省高校新世纪优秀人才支持计划项目(GYZ-160144)；福建工程学院科研发展基金(GYZ-160126)

2016-06-23 修改稿收到日期： 2016-09-15

吴琛 女，博士，教授，硕士生导师，1978年生

TN911.72; TB123

A

10.13465/j.cnki.jvs.2017.22.028