薄壁管拉扭复合相变波的实验研究

王 波， 张 科， 唐志平

(中国科学技术大学 中国科学院材料力学行为和设计重点实验室，合肥 230026)

薄壁管拉扭复合相变波的实验研究

王 波， 张 科， 唐志平

(中国科学技术大学 中国科学院材料力学行为和设计重点实验室，合肥 230026)

为了观察相变波在复合应力加载条件下的传播特性，通过一套薄壁管预扭冲击拉伸的实验装置，对相变材料NiTi合金薄壁管进行了预扭冲击拉伸的实验研究。实验观察到明显的拉扭耦合快波结构，证明了复合应力下相变波确实具有耦合特性，此外，实验结果还表明相变材料NiTi合金在拉扭复合应力下的相变临界点具有明显的率无关性。由于拉扭耦合慢波部分的应变变化较小，在实验波形中不易分辨，对实验过程进行了数值模拟，模拟结果和实验基本吻合，并能观察到相应的耦合慢波部分。

复合应力；薄壁管；冲击拉伸；应力波；相变

相变会强烈的影响材料的力学行为，在材料的冲击相变领域，已经有了广泛的研究成果[1-3]，近年来，相变波以及相边界的传播问题越来越引起关注，并取得了一系列的研究结果[4- 5]，但是，大部分的工作主要集中在一维相变纵波上。对于复合应力下相变行为的研究，目前主要集中在准静态条件下，Sittner等[6]对相变材料薄壁管进行了准静态拉扭实验，发现了相变响应行为在准静态复合应力下的一些特征，越来越多的相变本构研究[7-10]也开始考虑复合应力的影响，但是依然以准静态研究为主。动态复合应力下的相变情况，尤其是相变波的传播问题的研究还相对较少，并且以理论分析为主[11-12]，目前还没有对复合应力相变波进行直接观察的相关实验报道。

常见的实现复合应力加载条件的实验手段主要有两种，分别为平板的压剪以及薄壁管的拉(压)扭，其优点在于应力状态或应变状态相对简单，都只包含特定的应力分量或应变分量，使得既能研究复合应力下材料或结构响应的特点，又能排除不关心的分量的影响。Yang等[13-14]曾经使用轻气炮对相变材料NiTi合金进行了一维应变平板压剪实验，以研究应力诱发下的马氏体相变，由于测量的是背表面的粒子速度，而相变波的传播较慢，故仅能观察到弹性前驱波以及相变波的波前状态，没能观察到压剪复合相变波本身的传播情况。薄壁管的拉(压)扭方面，Lipkin等[15-18]的研究组曾经在霍普金森压杆的基础上建立了一套薄壁管预扭冲击压缩的实验装置，并分别对率无关材料3003铝以及率相关材料α-Ti进行了实验研究，观察到了相应的压扭耦合塑性波的传播情况。

从研究复合应力相变波的传播角度出发，薄壁管的预扭冲击实验较为可行，参考Lipkin等对弹塑性材料的预扭冲击压缩实验，我们选取了相变材料NiTi合金薄壁管进行了预扭冲击压缩的实验尝试。然而，由于NiTi合金的压缩相变点较高，需要的加载幅值也较高，但材料偏脆性，实验中常常在加载幅值没有达到薄壁管的压缩相变点时，薄壁管的局部就发生了断裂，无法在实验中观察到复合应力相变波的传播情况。考虑到NiTi合金具有拉压不对称性，拉伸比压缩更容易进入相变，并且拉伸相比压缩，可以避免屈曲的产生，我们最后选择对NiTi合金薄壁管进行预扭冲击拉伸加载，并成功在实验中观察到了NiTi合金中的拉扭复合相变波。

1 实验原理及装置

Song等从特征线理论出发，对薄壁管中的复合应力相变波的传播特性进行了理论预测。对于如图1所示的相变材料薄壁管，当端面受到轴向力F以及力矩M的冲击加载的时候，拉伸波和剪切波将沿X方向传播。在发生相变之前，薄壁管中传播的是相互独立的一维弹性拉伸波以及一维弹性剪切波，如果加载到了材料的相变点，理论上将会产生相变耦合波，耦合波中拉伸分量和剪切分量以相同的速度传播，并满足特定的相容关系。相变耦合波分为两种，分别为波速范围介于弹性纵波和弹性横波的波速之间的相变耦合慢波以及波速范围介于0到弹性横波的波速之间的相变耦合慢波。对于NiTi合金，Song等给出了σ-τ空间中的应力路径分布情况，如图2所示。初始相变面在σ-τ空间中为一偏心的椭圆，初始相变面外为相变区。在相变区内，相变耦合快波和相变耦合慢波的路径成网状分布，同一应力状态点处的两种波系路径相互垂直，并且沿着图2中箭头的方向，耦合波的波速会发生递减。

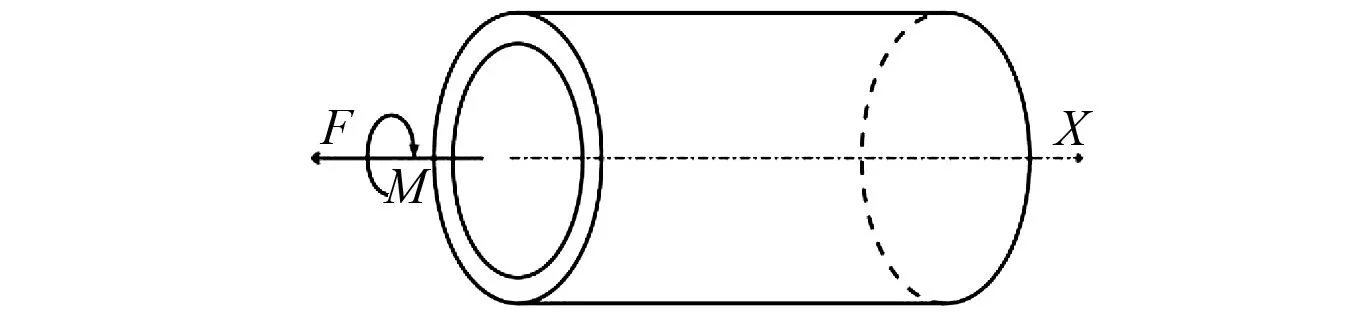
图1 薄壁管受力示意图Fig.1 The thin walled tube under tension and torsion

对薄壁管同时施加轴向冲击以及动态扭转在实验技术上较难实现，而预先进行扭转并保持扭转角度，然后进行轴向冲击的方法不仅更容易实现，而且理论上同样能产生耦合快波以及耦合慢波。通常的预扭冲击实验为预扭后进行冲击压缩，然而NiTi合金的压缩相变点较高，并且材料偏脆性，管端保持扭转角度的部分在冲击压缩下常常先发生断裂，使得扭转角度无法保持，此外，理论预测中，在τ轴和椭圆形相变临界面的短轴之间的波系传播也相对复杂，不利于波形分析。考虑到相变材料NiTi合金具有拉压不对称性，拉伸方向更容易进入相变，并且拉伸方向的波系传播情况相对简单，利于分析，我们采用对相变材料NiTi合金薄壁管施加扭转并保持，随后进行冲击拉伸的方式来产生复合应力相变波。

实验时先将薄壁管纯扭转至相变区某一应力点，如图2中点A所示，随后进行进行冲击拉伸，最终的应力值为第一象限的某一应力点，如图2中点C所示。过点A的耦合快波路径和过点C的耦合慢波路径交于点B，由于相变波在应力空间中必须沿着耦合快波或耦合慢波的路径发展，并且耦合快波的波速大于耦合慢波，所以薄壁管中的波系结构理论上为A-B的耦合快波以及B-C的耦合慢波。

图2 相变耦合波的应力路径Fig.2 The stress path of coupling waves

实验在一套基于霍普金森压杆基础上改造的预扭冲击拉伸实验装置[19]上进行，图3为薄壁管受预扭冲击拉伸实验的示意图，在薄壁管的一端内侧黏接一圆柱，称这一端为闭口端，另一端外侧黏接一圆环，称为开口端，闭口端和开口端的圆柱及圆环都固定有销钉，可在两端套筒的滑槽中沿轴向滑动。其中，闭口端的套筒不可旋转，开口端的套筒可绕轴向旋转任意角度并保持。入射杆由薄壁管的开口端插入，与闭口端的圆柱贴合。开始实验前，旋转开口端的套筒到一定角度并固定，使薄壁管整体进入扭转相变区，随后通过霍普金森压杆在入射杆中产生一道压缩方波。压缩方波到达闭口端后，会传入圆柱块并在自由面发生反射，使得圆柱块向后运动，通过黏接层的传递，最终在薄壁管中形成一道拉伸载荷。在靠近管拉伸信号输入端的方向对称粘贴应变花，应变花的三个敏感栅与轴向的夹角分别为±45°以及0°，通过±45°方向上的线应变，可以反算出剪应变的值，0°方向上的敏感栅测量的为轴向应变。

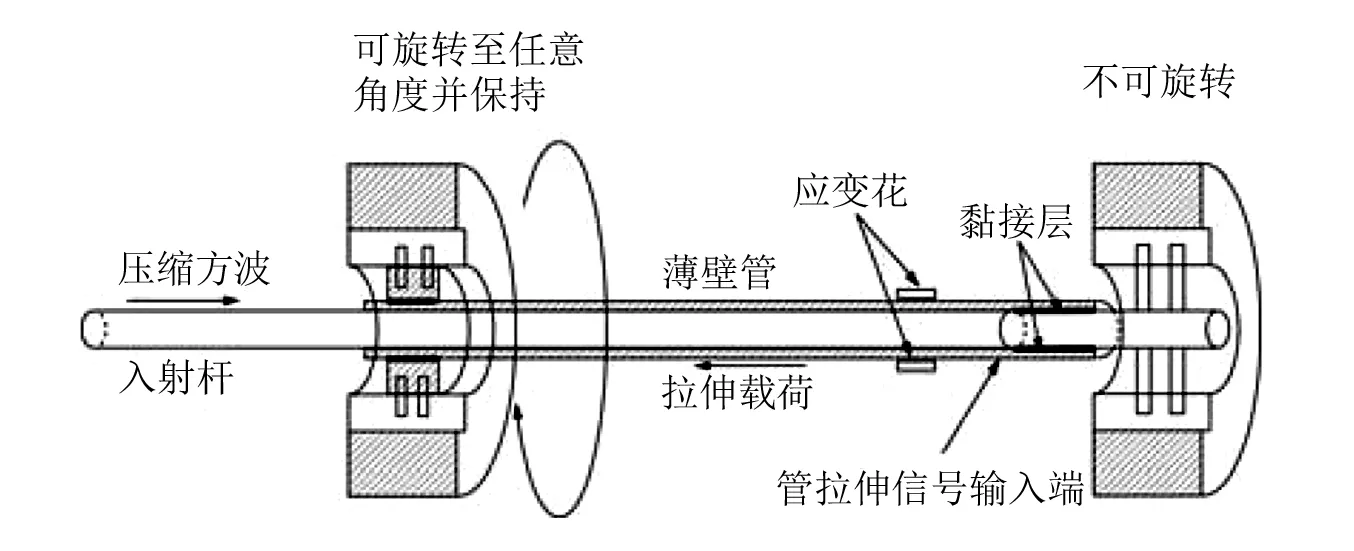
图3 薄壁管预扭冲击拉伸示意图Fig.3 The schematic diagram of the device

2 实验结果及讨论

实验中所用薄壁管为近等原子比NiTi合金薄壁管，外径为8 mm，内径7.26 mm，长600 mm。材料在室温下处于奥氏体相，其加卸载过程符合NiTi合金的伪弹性特性，当加载达到马氏体相变起始点时，开始相变，由奥氏体相进入混合相，材料模量降低，如果进一步加载到马氏体相变完成点，则材料将按照马氏体相弹性曲线进行响应。当材料从混合相区或马氏体相区进行卸载时，首先进行弹性卸载，达到相应的奥氏体相变起始点时，开始进行奥氏体相变，模量发生改变，奥氏体相变完成后，材料继续弹性卸载回到原点，如图4所示。实验过程中，由于卸载过程并不干脆，并且薄壁管另一端的反射信号紧接着卸载信号，所以目前仅研究加载过程，即马氏体相变过程中产生的相变波。

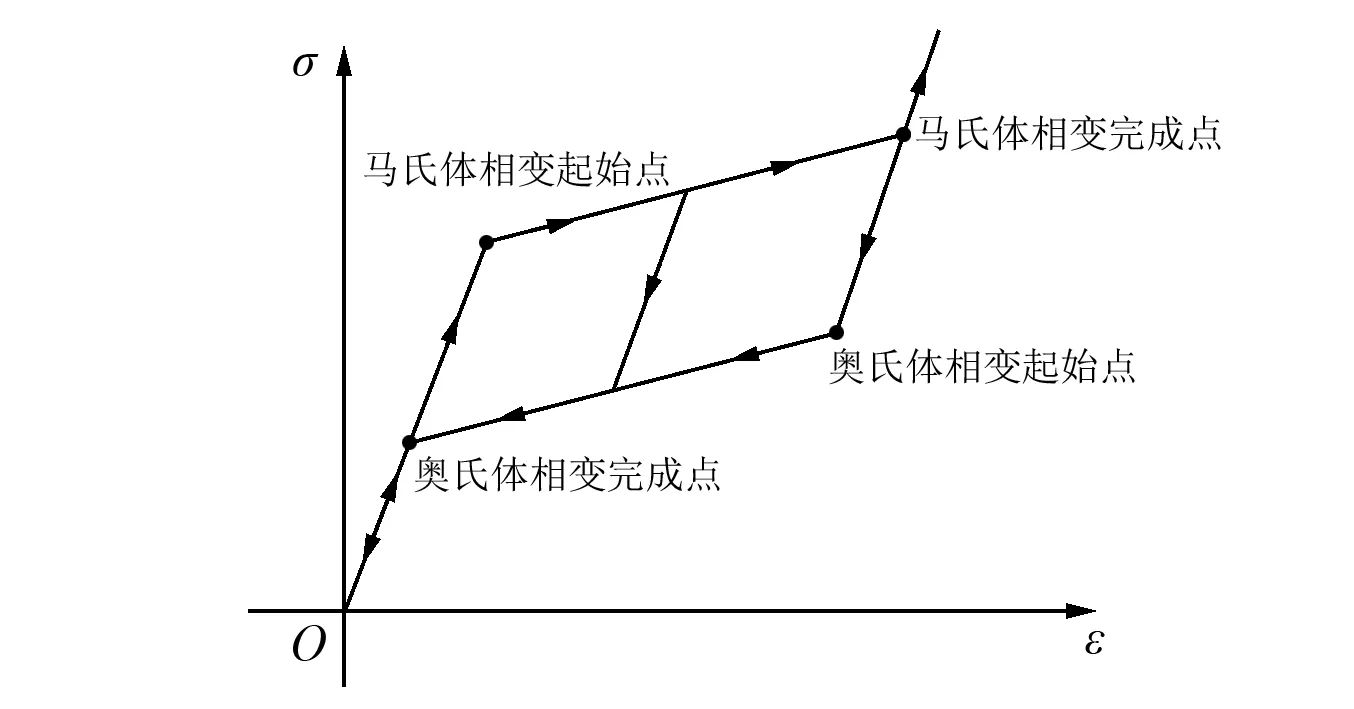
图4 NiTi合金加卸载过程示意Fig.4 Loading and unloading curve of NiTi

2.1 薄壁管纯冲击拉伸

在进行预扭冲击拉伸实验前，为了观察产生的拉伸载荷的特性，首先进行了纯冲击拉伸实验。保持开口端和闭口端的滑槽角度相同，此时薄壁管受到的扭转载荷始终为0。实验中子弹直径为12 mm，长500 mm，入射杆有两种，一种直径为12 mm，长1 500 mm，一种直径为6.8 mm，共两根，每根长450 mm，其中6.8 mm的入射杆插入薄壁管内部。子弹首先撞击直径12 mm的入射杆，理论上会产生一道约195 μs的压缩方波，压缩方波随后传入直径6.8 mm的入射杆中，获得更高幅值的一道压缩方波，再经过闭口端以及黏接层的传递，最终将会在薄壁管中产生一道拉伸载荷，典型结果如图5所示。

从图5可知，入射杆中的压缩方波最终转换成了NiTi管中的一道拉伸方波。与入射杆中的压缩信号相比，NiTi管中的拉伸信号的脉宽略有缩短，约185 μs，拉伸信号上升沿的时间显著变长，从压缩信号10 μs左右变长到65 μs左右。此外，上升沿分成了斜率不同的两段，其中，第一段约25 μs左右，上升至最终幅值的75%左右。由于图5所示的纯冲击拉伸实验中的子弹速度并不高，薄壁管中的拉伸应变也比较低，约0.4%，而NiTi合金的拉伸相变点通常在0.7%左右，所以图5对应的纯冲击拉伸实验理论上传播的应该是纯弹性纵波。改变子弹的撞击速度，拉伸信号的幅值跟着改变，但脉宽基本不变，此外，上升沿同样会分成两段，并且对应的时间以及幅值比例基本类似。我们认为拉伸载荷的这一特点可能是入射杆中的压缩信号在薄壁管闭口端转换为拉伸信号的复杂过程中造成的，属于装置的固有特点。

图5 纯冲击拉伸典型波形Fig.5 The wave of tensional experiment

2.2 薄壁管预扭冲击拉伸

旋转薄壁管开口端的套筒，使预扭剪应变达到1.2%左右，固定套筒的旋转角度，保持预扭载荷，随后进行冲击拉伸，薄壁管中的典型实验信号如图6所示，应变花距离拉伸信号输入端100 mm。

图6 预扭冲击拉伸典型实验信号Fig.6 The wave of impact tension on a pre-torqued tube

从图6可知，在拉伸载荷到达测量位置前，薄壁管保持预扭状态，纵向应变为0，剪切应变约为1.2%，记此应变点为A’，随着拉伸载荷的到达，纵向应变增加到0.88%左右，同时剪切应变减小到0.96%左右，记此应变点为B’，A’-B’这一区域的应变变化特征与理论预测的相变耦合快波区的变化特征一致，表明A’-B’为相变耦合快波区。此外，点A’处纵向信号和剪切信号同时起跳，表明点A’处的动态相变临界点和静态预扭下的相变临界点一致，没有与应变率相关的强化效应，说明在复合应力情况下，相变临界点与应变率无关。A’-B’区域内，纵波上升沿有一拐点，与之前纯冲击拉伸实验中拉伸载荷上升沿的情况类似，说明该拐点是由于拉伸载荷上升沿本身的形状特点造成的，与拉扭复合相变波的传播特性无关。点C’处拉伸信号开始卸载，纵向应变约为0.90%，剪切应变约为1.09%，理论上B’-C’应该包含恒值应变区以及相变耦合慢波区，然而由于慢波部分所对应的应变变化较小，而纵向应变和剪切应变信号本身的绝对值较大，目前的实验波形中暂时并不能清晰的区分出来慢波部分的结构。

2.3 数值模拟

为了区分出慢波部分的波系结构，也为了对实验结果和理论预测进行比较，我们需要得到实验过程的理论预测解。尽管从理论解出发，可以给出实验波形和应变路径的理论预测，但是由于理论解中考虑的是理想的瞬时突加载荷，与实际情况并不相同，无法反映实际情况中加载过程的影响，我们从理论解所用本构模型出发，采用有限差分法对实验过程进行了数值模拟，将模拟结果作为NiTi合金薄壁管预扭冲击拉伸的理论预测解。

薄壁管复合拉扭的控制方程为

σX=ρ0ut

(1)

τX=ρ0vt

(2)

uX=εt

(3)

vX=γt

(4)

式中：ρ0为密度；σ,τ分别为纵向应力和剪应力;u和v分别为纵向粒子速度和环向粒子速度；ε和γ分别为纵向应变和剪切应变。

材料在没有进入相变区时，可采用弹性本构，进入相变后，本构采用理论预测中所用本构，简单回顾如下，材料在相变区满足

(5)

式中：α为拉压不对称系数；θ=[3/(1-α2)]0.5；β=-θα，相变起始时的k为k0。令θv=θ+β，σv=σ-βk，则材料符合如下的增量型本构

(6)

(7)

式中：E为杨氏模量；μ为弹性剪切模量；g为一维拉伸时混合相的的模量。

采用lax格式对控制方程式(1)～式(4)进行有限差分，结合本构方程式(6)，即可对薄壁管预扭冲击拉伸进行数值模拟，模拟所用参数如表1所示。

表1 模拟所用参数

为同时满足迎风条件以及lax格式的网格黏性很小的条件，采用100 m，100 s，1 kg作为计算中的量纲单位，模拟中采用时间步为Δt=1×10-10，网格大小为ΔX=1×10-6，共10 001个网格点。由纯拉伸实验知拉伸载荷的上升沿分为两段，其中第一段约25 μs，占总加载幅值的75%左右，以此作为边界条件，进行模拟。

模拟结果和实验结果的对比如图7所示。从图7可知，模拟结果和实验结果基本吻合。A’-B’段的拉扭耦合快波部分无论是实验结果还是模拟结果，结构都比较清晰。至于B’-C’段，实验波形由于变化较小，且实验中信号可能存在一定的波动和误差，仅从实验波形很难区分出拉扭耦合慢波部分，但是通过模拟，我们可以从模拟信号中区分出来两部分，分别为B’-D’的恒值区部分以及D’-C’的耦合慢波部分，这一点与理想的瞬时突加载荷的预测结果是一致的，从图7还可知，模拟结果中B’-D’段的恒值区对应的平台时间并不长，同时D’-C’的耦合慢波部分的应变变化确实较小，因此造成了实验波形中慢波部分的结构不明显。尽管实验中慢波部分结构不明显，由于模拟结果和实验结果吻合较好，且模拟中能够区分出来恒值区部分和耦合慢波区部分，我们认为实验中的B’-C’段也应当经历了和模拟结果相似的过程。

由实验波形以及模拟结果，可以得到卸载前NiTi合金薄壁管中的拉扭复合相变波在应变空间中的路径情况，如图8所示，其中A’-B’段对应的为拉扭耦合快波，D’-C’段对应的为拉扭耦合慢波，其基本结构也与图2中应力空间中的路径结构基本一致，与理论预测相符，由实验波形的D’-C’的应变路径也可以看出，实验过程中应当确实存在耦合慢波部分。

图7 模拟和实验的对比Fig.7 The comparison of simulation and experiment

图8 实验以及模拟中的应变路径Fig.8 The strain path of experiment and simulation

3 结 论

在相变波的研究中，考虑复合应力影响的研究相对较少，复合应力下相变波本身传播情况的实验研究则几乎没有。本文通过对相变材料NiTi合金薄壁管进行预扭冲击拉伸实验，成功观察到了拉扭复合应力下相变波的传播情况。

实验结果表明在预扭冲击拉伸实验中，会出现与理论预测基本一致的相变耦合快波，表明复合应力条件下，相变波的传播确实具有耦合特性。实验结果中，与理论预测的相变耦合慢波区相对应部分的应变变化值较小，而所处的应变状态点本身的绝对值相对较大，实验精度可能会受到影响，故实验波形中相变耦合慢波部分的结构并不明显。对实验过程进行数值模拟，我们得到了与实验波形较吻合的模拟结果，并能在模拟结果中区分出耦合慢波部分的波系结构，表明实验过程中应当确实存在耦合慢波部分。

此外，实验结果还表明，相变材料NiTi合金的相变临界准则在复合应力情况下具有率无关的特点。

[ 1 ] 唐志平. 冲击相变[M]. 北京: 科学出版社,2008.

[ 2 ] DUVAL G E, GRAHAM R A. Phase-transitions under shock-wave loading[J]. Rev Mod Phys, 1977, 49(3): 523-579.

[ 3 ] 唐志平. 冲击相变研究的现状与趋势[J]. 高压物理学报, 1994, 8(1): 14-22.

TANG Zhiping. Some topics in shock-induced phase transitions[J]. Chinese Journal of High Pressure Physics, 1994, 8(1): 14-22.

[ 4 ] CHEN Y C, LAGOUDAS D C. Wave propagation in shape memory alloy rods under impulsive loads[C]//Proceedings Mathematical, Physical and Engineering Sciences, 2005, 461: 3871-3892.

[ 5 ] BEREZOVSKI A, MAUGIN G A. Stress-induced phase-transition front propagation in thermoelastic solids[J]. European Journal of Mechanics-A/Solids, 2005, 24(1): 1-21.

[ 6 ] SITTNER P, HARA Y, TOKUDA M. Experimental study on the thermoelastic martensitic transformation in shape memory alloy polycrystal induced by combined external forces[J]. Metallurgical and Materials Transactions A, 1995, 26(11): 2923-2935.

[ 7 ] QIDWAI M A, LAGOUDAS D C. On thermomechanics and transformation surfaces of polycrystalline NiTi shape memory alloy material[J]. International Journal of Plasticity, 2000, 16(10/11): 1309-1343.

[ 8 ] 郭杨波，唐志平，徐松林. 一种考虑静水压力和偏应力共同作用的相变临界准则[J].固体力学学报, 2004, 25(4): 417-422.

GUO Yangbo, TANG Zhiping, XU Songlin. A critical criterion for phase transformation considering both hydrostatic pressure and deviatoric stress effects[J]. Acta Mechanica Solida Sinica, 2004, 25(4): 417-422.

[ 9 ] SALEEB A F, PADULA S A, KUMAR A. A multi-axial, multimechanism based constitutive model for the comprehensive representation of the evolutionary response of SMAs under general thermomechanical loading conditions[J]. International Journal of Plasticity, 2011, 27(5): 655-687.

[10] LAGOUDAS D, HARTL D, CHEMISKY Y, et al. Constitutive model for the numerical analysis of phase transformation in polycrystalline shape memory alloys[J]. International Journal of Plasticity, 2012, 32/33(2): 155-183.

[11] SONG Q, TANG Z. Combined stress waves with phase transition in thin-walled tubes[J]. Applied Mathematics and Mechanics, 2014, 35(3): 285-296.

[12] WANG B, TANG Z. Study on the propagation of coupling shock waves with phase transition under combined tension-torsion impact loading[J]. Science China Physics Mechanics amp; Astronomy, 2014, 57(10): 1977-1986.

[13] YANG S Y, ESCOBAR J, CLIFTON R J. Computational modeling of stress-wave-induced martensitic phase transfor-mations in NiTi[J]. Mathematics and Mechanics of Solids, 2009, 14(1/2): 220-257.

[14] ESCOBAR J C, CLIFTON R J, YANG S Y. Stress-wave-induced martensitic phase transformations in NiTi[C]// AIP Conference Proceedings. [S. l.]: AIP, 2000: 267-270.

[15] LIPKIN J, CLIFTON R J. Plastic waves of combined stresses due to longitudinal impact of a pretorqued tube—Part 1: experimental results[J]. Journal of Applied Mechanics, 1970, 37(4): 1107-1112.

[16] LIPKIN J, CLIFTON R J. Plastic waves of combined stresses due to longitudinal impact of a pretorqued tube—Part 2: comparison of theory with experiment[J]. Journal of Applied Mechanics, 1970, 37(4): 1113-1120.

[17] HSU J C C, CLIFTON R J. Plastic waves in a rate sensitive material—I. Waves of uniaxial stress[J]. Journal of the Mechanics and Physics of Solids, 1974, 22(4): 233-253.

[18] HSU J C C, CLIFTON R J. Plastic waves in a rate sensitive material—II. Waves of combined stress[J]. Journal of the Mechanics and Physics of Solids, 1974, 22(4): 255-266.

[19] 王波, 唐志平. 薄壁管预扭冲击拉伸实验装置的研制[J]. 实验力学, 2016, 31(3): 299-305.

WANG Bo, TANG Zhiping. Development of a device for impact tension of pre-torqued thin walled tube[J]. Journal of Experimental Mechanics, 2016, 31(3): 299-305.

Anexperimentalstudyonthestresswaveswithphasetransitionundercombinedtension-torsionloading

WANG Bo ，ZHANG Ke ，TANG Zhiping

(CAS, Key Laboratory of Mechanical Behavior and Design of Materials (LMBD),University of Science and Technology of China, Hefei 230026, China)

In order to investigate the propagation of stress waves with phase transition under combined stress loading conditions, impact tension loading was applied on a pre-torqued thin walled tube made of NiTi alloy, which transformed its phase under stress loading. The coupling fast waves were observed, proving that the stress waves with phase transition under combined loading were coupling. The results show that the critical criterion for phase transition under combined stress is rate-nonsensitive. The signal of coupling slow waves was very small. A simulation was performed, which fit well with the experiment. The coupling slow waves could be distinguished.

combined stress; thin walled tube; impact tension; stress waves; phase transition

国家自然科学基金(11072240；11272311)

2016-05-20 修改稿收到日期： 2016-08-09

王波 男，博士生，1988年生

唐志平 男，硕士，教授，1945年生

O347

A

10.13465/j.cnki.jvs.2017.22.005