均匀流下柔性立管涡激振动响应及涡激力载荷特性研究

宋磊建， 付世晓， 任 铁,3， 于大鹏， 张萌萌

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240； 2. 上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240；3. 中国船舶及海洋工程设计研究院，上海 200011； 4. 海军装备研究院，北京 100161)

均匀流下柔性立管涡激振动响应及涡激力载荷特性研究

宋磊建1,2， 付世晓1,2， 任 铁1,2,3， 于大鹏4， 张萌萌1,2

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240； 2. 上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240；3. 中国船舶及海洋工程设计研究院，上海 200011； 4. 海军装备研究院，北京 100161)

采用模型试验的方法研究了均匀流下柔性立管的涡激振动(VIV)响应特性及涡激力载荷特性。对均匀流场中柔性立管的VIV响应特性进行了分析，而后通过欧拉-伯努利梁动态响应控制方程和最小二乘法求取了柔性立管顺流向(IL)和横流向(CF)的涡激力系数。研究结果表明：均匀流下柔性立管的VIV为位移和主导频率不随时间变化的稳态响应，顺流向涡激振动的主导频率为横流向的2倍；柔性立管的激励系数与强迫振动试验获得的系数不一致，无因次频率处于激励区间的激励系数存在负值，激励系数不仅和无因次频率及无因次振幅相关，还与CFamp;IL方向位移相位角相关；在无因次频率0.13～ 0.22时，横流向的附加质量系数在1.5～ 3.0振荡变化；而顺流向的附加质量系数在无因次频率在0.26～ 0.42内从-1.0迅速增大到1.2后基本保持不变。

柔性立管; 涡激振动；涡激力; 激励系数；附加质量系数

在洋流作用下，立管两侧会出现交替的泄涡，当泄涡频率接近于立管某一阶固有频率时，会引起立管在顺流向(In-Line, IL)及横流向(Cross-Flow, CF)发生振动，即：涡激振动(Vortex-Induced Vibration, VIV)。VIV的出现会使得立管产生严重的疲劳损伤。因此准确预测立管的VIV在立管的设计中占有重要地位。在立管VIV的预报中，涡激力载荷的构建直接决定着立管VIV预报结果的准确性，而当前VIV的预报中对涡激力载荷的构建均是基于刚性圆柱体单自由度(纯CF或纯IL)强迫振荡试验建立的涡激力系数数据库，包括激励系数数据库和附加质量系数数据库进行的。在刚性圆柱体单自由度强迫振荡试验中假设立管CF方向的涡激振动与IL方向的涡激振动互不影响，圆柱体只在纯CF或纯IL方向上运动，忽略二者的耦合作用。然而，真实情况下，柔性立管的CF与IL方向均会发生VIV，且两个方向上的VIV相互耦合，这种运动上的耦合使得两个方向上的涡激力也相互影响，已有的研究表明，IL方向的VIV会使得CF方向涡激力的激励系数数据库产生新的峰值[1]。Sumer等[2]指出，当CF方向VIV振幅超过0.2D～0.3D时，脱落涡会变的整齐有序，泻涡强度增大，此时IL方向的涡激力会被明显放大。正是由于柔性立管双向VIV的这种耦合作用，使得当前对柔性立管VIV的预报结果不准确[3]，在海洋立管的设计中，不得不采用高达10倍以上的安全系数来确保其结构设计的安全性[4]。然而，随着油气开采进一步向更深的水域发展，仅靠提高设计安全系数仍然无法确保管线结构的安全，这极大地制约了油气开发向更深水域的发展。因此，研究柔性立管CF与IL方向均发生VIV时的涡激力载荷特性显得越来越重要。

计算流体力学方法(Computer Fluid Dynamics, CFD)是研究VIV这种复杂流固耦合问题的理想方法[5-6]。为了研究涡激振动发生时柔性立管的水动力特性，Yamamoto等[7]采用直接涡流法估算柔性立管的水动力，并利用准3维数值模型研究柔性立管的振动与其水动力之间的关系。Evangelinos等[8]利用直接数值模拟方法模拟刚性圆柱体以及柔性圆柱体的3 维流场，并得到了流场作用在刚性圆柱体和柔性圆柱体上的阻力。然而上述数值模拟结果均未得到试验的验证。此外，CFD对流场和结构的网格质量要求十分精细，其计算量特别巨大，即便是一个6 m长的试验立管，每个流速工况计算都需耗时数月[9]，因而目前采用CFD方法系统的研究细长柔性立管的涡激力是不太现实的。

鉴于CFD的局限性，Mukundan等[10-11]强迫振荡试验获得的激励系数数据库参数化，利用将经验模型VIVA预测结果与试验结果之间的误差最小化得到最优参数的方法，获得了CF方向上新的激励系数数据库，新的数据库具有更大的激励区间，且主激励区间与第二激励区间混合在一起。然而，Mukundan的方法不能用于研究立管CF方向VIV高阶响应下的涡激力以及IL方向的涡激力。Huarte等[12]利用试验中测得的剪切流下竖直顶张力立管模型CF与IL方向上的应变信息结合梁有限元方程得到了作用在立管CF与IL方向上的水动力载荷，然而其没有进一步获得立管CF与IL方向的涡激力系数，即：激励系数和附加质量系数。Wu等[13-14]分别利用梁有限元状态矢量空间方程和基于最优控制理论的逆分析法获得了剪切流下立管CF方向上的涡激力及其载荷系数，然而二者均没有对立管IL方向上的涡激力进行研究。

本文通过利用拖车拖动两端承受恒定预张力的柔性立管模型在拖曳水池中做匀速运动的方法，研究均匀流下CF与IL方向均发生VIV时的柔性立管VIV响应特性及涡激力特性。文中利用试验中测得的立管模型的VIV应变信息，采用FFT(Fast Fourier Transform)、小波分析法和模态分析法研究均匀流场中柔性立管CF与IL方向上的VIV响应特性。同时，利用欧拉-伯努利梁动态响应控制方程和最小二乘法求取VIV发生时柔性立管CF与IL方向的涡激力系数，包括激励系数和附加质量系数。

1 试验描述

本试验在拖曳水池中进行，水池尺寸为192 m×10 m×4.2 m(长×宽×深)，立管模型横置于水池中，其中心距离水面1.5 m，试验装置示意图如图1所示。立管模型利用万向节与端部装置进行连接，可在IL与CF方向上弯曲并可以沿轴向方向运动。端部装置可以为立管模型提供恒定预张力。试验中均匀来流的模拟方法是将立管横置于拖曳水池中，由拖车带动立管在拖曳水池中匀速前进，从而形成相对均匀来流。

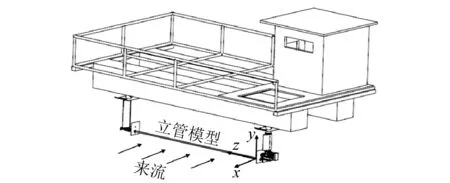
图1 试验模型简图Fig. 1 Schematic of the test apparatus

试验中所使用的立管模型为缩尺模型，模型的外径为30 mm，有效长度为7.9 m，模型具体参数如表1所示。表1中的结构阻尼比为立管模型在空气中的结构阻尼比。

表1 立管模型基本参数

立管模型表面布置有88个光纤光栅应变传感器，分别布置于模型的CF1、CF2、IL1以及IL2四个方向，用于测量模型在此四个方向上的应变，即εCF1、εCF2、εIL1和εIL2，如图2所示。其中CF1和CF2方向上的传感器分别为19个，IL1和IL2方向上分别为25个。传感器在CF与IL方向上均匀分布，CF与IL方向上相邻测点的间距分别为0.42 m和0.315 m。光纤光栅传感器的采样频率为250 Hz。

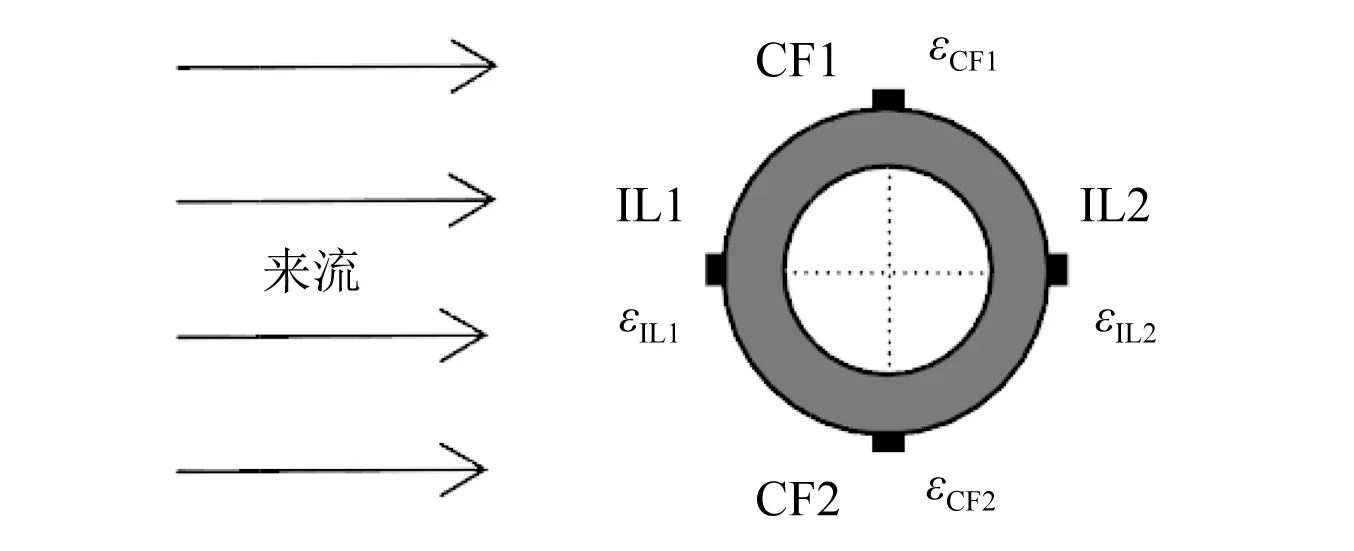
图2 立管模型表面光纤光栅传感器布置方式Fig. 2 Arrangement of strain gauges on the surface of the riser model

2 数据处理

2.1 涡激振动产生的弯曲应变

试验中受预张力的立管模型，由光纤光栅应变传感器测量的立管模型CF方向各测点处的应变εCF1和εCF2均包含两部分:轴向张力产生的拉伸应变εCF-T以及VIV产生的弯曲应变εCF

εCF1=εCF-T+εCF
εCF2=εCF-T-εCF

(1)

对式(1)进行简单的变换, 便可得到CF方向由VIV引起的弯曲应变εCF

εCF=[εCF1-εCF2]/2

(2)

立管模型IL方向各测点处由光纤光栅应变传感器测量的应变εIL1和εIL2包含三部分：张力产生的拉伸应变εIL-T、VIV产生的弯曲应变εIL以及平均拖曳力产生的弯曲应变εmb

εIL1=εIL-T+εIL+εmb
εIL2=εIL-T-εIL-εmb

(3)

由于立管模型IL方向的VIV为均值为零的周期性振动，故由VIV引起的弯曲应变εIL的时间平均值为零，即

(4)

此外，由平均拖曳力产生的弯曲应变εmb不随时间变化，因此在试验稳定段内平均弯曲应变εmb满足

(5)

由式(3) 可以得到

εmb+εIL=[εIL1-εIL2]/2

(6)

对式(6)的两端求时间的平均值，结合式(5)和式(4)可得到立管模型IL方向各测点处由VIV引起的弯曲应变εIL

(7)

2.2 柔性立管涡激力载荷

将试验中所用的立管模型理想化为受张力的欧拉-伯努利梁[15]，在忽略立管模型轴向扭转变形的基础上，立管CF与IL方向上的VIV可以通过欧拉-伯努利梁的结构动力学方程进行描述。定义坐标系O-XYZ：坐标系的原点位于立管模型的某一端点；Z轴沿立管的轴向方向；X轴沿来流方向，即IL方向；Y轴与X轴和Z轴相互垂直，即CF方向，如图1所示。在此坐标系下，立管模型CF和IL方向VIV的控制方程可表示为

(8)

(9)

式中：EI为立管模型的弯曲刚度；m为立管模型单位长度质量；C为立管模型在空气中的结构阻尼；T为VIV发生时立管两端轴向张力的时间平均值；fx(z,t)和fy(z,t)分别为使得立管在IL与CF 方向上发生VIV的涡激力；x(z,t)和y(z,t)分别为立管模型IL与CF方向VIV的位移；∂y(z,t)/∂t与∂2y(z,t)/∂t2分别为立管模型CF方向VIV的速度和加速度；∂x(z,t)/∂t与∂2x(z,t)/∂t2分别为立管模型IL方向VIV的速度和加速度。

立管IL与CF方向的VIV位移x(z,t)和y(z,t)可由式(2)和式(7)求得的立管CF与IL方向的VIV弯曲应变结合模态分析法[16]求得。立管CF与IL方向的VIV速度和加速度可由对VIV位移求时间的一阶偏导和二阶偏导获得。

2.3 柔性立管涡激力载荷系数

本节中将给出柔性立管CF与IL方向涡激力载荷系数，即：激励系数与附加质量系数的求解方法。以立管CF方向为例。

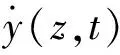
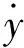
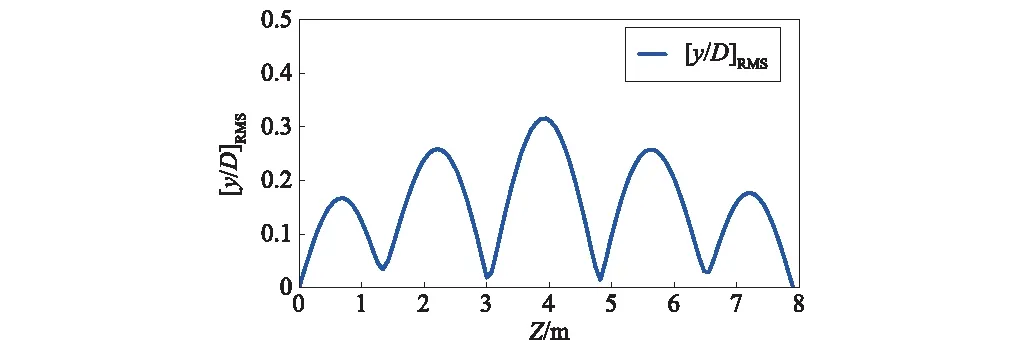
(10)

式中：y0(z)为横截面z处的VIV位移响应幅值；ω为立管模型CF方向VIV响应圆频率。

在此情况下，立管横截面z处的涡激力载荷fy(z,t)可表示为

fy(z,t)=f0(z)sin(ωt+φ(z))

(11)

式中：f0(z)为涡激力载荷的幅值；φ(z)为横截面z处的涡激力与此横截面处VIV位移之间的相位角。将式(11)展开，可得

fy(z,t)=f0(z)sin(φ(z))cos(ωt)-
[-f0(z)cos(φ(z))sin(ωt)]

(12)

式中,f0(z)sin(φ(z))cos(ωt)为与速度同相位的涡激力，可将其表示为

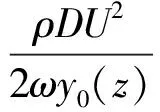
(13)

式中：CLe(z)为横截面z处的激励力系数；ρ为流体密度；U为流速；D为立管模型的水动力直径。

式(12)中的-f0sin(φ)cos(ωt)项为与加速度同相位的涡激力，即附加质量力，可以表示为

(14)

式中,CLa(z)为横截面z处的附加质量系数。

由式(13)和式(14)可得横截面z处的涡激力载荷fy(z,t)表示为

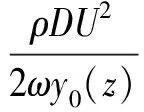
(15)

若已知立管横截面z处的VIV涡激力载荷以及VIV

响应速度和加速度后，可采用最小二乘法求解立管横截面z处的激励系数CLe(z)和附加质量系数CLa(z)，具体过程为:

将根据式(8)计算得到的VIV涡激力载荷fy(z,t)看作为t时刻立管横截面z处涡激力载荷的测量值，将fp(z,t)看作同一时刻立管横截面z处涡激力载荷的预测值，如式(16)表示

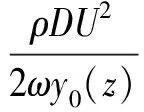
(16)

根据最小二乘法基本原理，激励系数CLe(z)和附加质量系数CLa(z)的选取要使得整个采样时间内涡激力载荷的预测值与测量值误差的平方和为最小

(17)

式中：n为整个采样时间内的采样点个数；e2(z)为整个采样时间内立管横截面z处涡激力载荷预测值与测量值误差的平方和。

将式(17)的右边项进行展开，可得

(18)

令

则式(18)可简化为

(19)

若要使得激励系数CLe(z)和附加质量系数CLa(z)的选取使得e2(z)为最小，则

(20)

结合式(19)和式(20)，可得

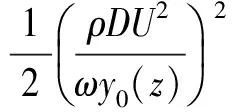
(21)

由式(21)可求得立管横截面z处CF方向上的VIV激励系数CLe(z)和附加质量系数CLa(z)，如式(22)所示

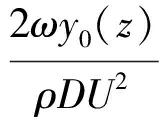
(22)

柔性立管IL方向上各横截面处的VIV激励系数Cde(z)和附加质量系数Cda(z)可采用与CF方向同样的方法求得。

3 结果分析与讨论

3.1 立管模型VIV响应特性

流速2.6 m/s下立管模型在测点Z=3.95 m处CF与IL方向VIV弯曲应变的时历曲线、频率谱及小波分析结果，如图3所示。从图3可知：①立管模型CF和IL方向上的VIV均为幅值稳定的稳态振动；②立管模型CF与IL方向VIV的主导频率分别为16.79 Hz和33.62 Hz，立管模型CF与IL方向上VIV的主导频率随时间的发展均保持不变，且IL方向上的主导频率约为CF方向上主导频率的2倍，Fu等[18-19]都发现了VIV的这种双倍频率现象；③立管CF方向的VIV出现了明显的3倍主导频率的高阶响应，Vandiver等[20]也发现了VIV的这种高阶响应。

图 3 流速2.6 m/s下立管模型CF与IL方向上测点Z=3.95 m处VIV应变时历、频率谱及小波分析结果Fig. 3 Time histories, frequency spectra and result of the wavelet analysis of strain because of VIV in the CF and IL directions at Z=3.95 m for a 2.6 m/s current

本文只关心立管模型CF与IL方向主导频率下的VIV响应及其涡激力，故采用带通滤波对采集到的立管模型的VIV应变信号进行滤波处理，从而获得主导频率下的VIV响应。流速2.6 m/s 下立管模型CF与IL方向的滤波宽度为15.0～18.0 Hz 和32.0～35.0 Hz。

在通过滤波得到流速2.6 m/s立管模型CF与IL方向主导频率下的VIV应变后，利用模态分析法求解立管模型CF与IL方向的VIV位移响应。图4为立管模型CF与IL方向VIV无因次位移RMS值([y/D]RMS和[x/D]RMS)沿立管轴向的分布。从图4可知，立管VIV响应的主导模态分别为5阶和7阶。如图4所示，立管模型CF方向的VIV位移响应远大于IL方向的VIV位移响应，而图3显示立管CF与IL方向的VIV应变在同一量级。这表明同一流速下，虽然立管CF方向的VIV位移大于IL方向的VIV位移，然而两个方向的VIV应变在同一量级，考虑到IL方向的VIV响应频率为CF的两倍，故而相比于CF方向的VIV，IL方向的VIV会使得立管产生同量级甚至更为严重的疲劳损伤。

3.2 柔性立管激励系数

(a)

(b)图4 流速2.6 m/s下立管模型CF与IL方向VIV的无因次位移RMS值沿轴向分布Fig. 4 Axial distributions of the RMS values of the non-dimensionalized VIV displacement in the CF and ILdirectionsfor a 2.6 m/s current

图5给出了流速2.6 m/s下立管模型CF与IL方向的VIV激励系数CLe和Cde以及无因次幅值(A/D)CF和(A/D)IL沿立管模型轴向的分布。图5显示在振动节点处，激励系数会发生突变，这是由于振动节点处的振动幅值太小导致的。基于刚性圆柱体强迫振荡试验的半经验频域预报理论指出无因次频率在0.125～0.2为VIV的激励区[21]，本试验中流速2.6 m/s下立管CF方向VIV的无因次频率为0.192，因此整个立管在CF方向应该均处于激励区；但从图5可知，立管模型某些区域内的激励系数CLe为负值，这表明均匀流速下，无因次频率处于激励区间的立管仍存在着激励区和阻尼区，在激励区内，能量从流场传到立管，而在阻尼区内，能量从立管传到流场。从图5还可知，在激励系数CLe为负值的区域内立管的无因次幅值并不总是最大的，这与Gopalkrishnan所发的规律是不一致的，Gopalkrishnan指出在同一无因次频率下，只有当幅值增大到某一值后，其激励系数才变为负值。此外，还可发现，同一流速，即同一无因次频率下，无因次幅值相同的立管各横截面处的激励系数并不相同，甚至差别很大，这是由于立管各横截面的运动轨迹以及CF与IL方向VIV位移相位角的不同，导致立管尾流区具有不同的泄涡模式，继而引起VIV水动力的变化[22]。这表明：柔性立管的激励系数不仅与无因次频率和无因次振幅相关，还与CFamp;IL方向的VIV位移相位角相关。立管IL方向上VIV的激励系数Cde沿立管轴向的分布规律与CF方向的激励系数CLe有类似的规律。

(a)

(b)图5 流速2.6 m/s下立管模型CF与IL方向激励系数及无因次位移幅值沿模型轴向分布Fig.5 Axial distributions of the CF and IL excitation coefficients and non-dimensionalized response amplitudes for a 2.6 m/s current

3.3 柔性立管附加质量系数

图6给出了流速2.6 m/s下立管模型CF与IL方向的附加质量系数CLa和Cda以及无因次幅值(A/D)CF和(A/D)IL沿立管模型轴向的分布。从图6可知，立管CF与IL方向的振动节点处，附加质量会发生突变，其原因与激励系数的一致。图6显示，均匀流场中当立管的CF与IL方向均发生VIV时，在同一流速，即同一无因次频率下，立管CF方向上不同无因次幅值下的附加质量系数并不相等，IL方向亦是如此。这与半经验频域预报模型VIVANA以及Aronsen[23]认为在一定的振动幅值范围内，附加质量系数与VIV振动幅值关系不大，只与无因次频率的结论并不一致。

(a)

(b)图6 流速2.6 m/s下立管模型CF与IL方向附加质量系数及无因次位移幅值沿模型轴向分布Fig. 6 Axial distributions of CF and IL added-mass coefficients and non-dimensionalized vibration amplitudes for a 2.6 m/s current

为了检验本文中用于计算立管模型涡激力载荷方法的正确性，利用图5和图6中的激励系数和附加质量系数，根据式(15)计算立管模型在流速2.6 m/s下CF与IL方向的涡激力。然后，根据表1中的立管模型参数在有限元软件ABAQUS中建立有限元模型，而后利用获得的涡激力计算立管模型的应变响应。图7为流速2.6 m/s下立管模型CF与IL方向测点Z=3.95 m处应变的测量值和计算值时历以及应变测量值和计算值的RMS沿立管轴向的分布。从图7可知，立管CF与IL方向应变响应的测量值和计算值非常吻合，这表明了本文中用于计算VIV发生时立管模型涡激力载荷的方法是正确的。

图7 流速2.6 m/s下立管模型CF与IL方向VIV应变的测量值及计算值在测点Z=3.95 m处的时历曲线以及应变RMS值沿立管轴向的分布Fig.7 Time histories of the measured and calculated values of CF and IL VIV strains at Z=3.95 m and axial distributions of the RMS values of the measured and calculated strains for a 2.6 m/s current

3.4 柔性立管平均附加质量系数

为了研究附加质量系数与无因次频率之间的关系，忽略VIV振幅对附加质量系数的影响，将附加质量系数在整个立管模型上进行平均，得到试验中各流速下CF与IL方向上的平均附加质量系数。根据立管模型的参数，建立立管模型的有限元模型，并将得到的平均附加质量系数带入到有限元模型中，计算立管模型CF与IL方向VIV主导模态对应的固有频率，将其与试验测得的主导频率相比较，如图8所示。从图8可以看出，利用平均附加质量系数计算得到的主导频率与试验测量值几乎相同。这表明虽然当CF与IL方向同时发生VIV时，立管CF与IL方向上各横截面处的附加质量系数不相等，但是在进行立管的VIV预报时，仍可以忽略VIV振动幅值对附加质量系数的影响，采用平均附加质量系数来计算立管的固有频率。

(a) CF

(b) IL图8 不同流速下立管模型CF与IL方向VIV主导频率的计算值和测量值Fig. 8 Comparison of the calculated and measured values of the dominant frequencies in the CF and IL direction fordifferent currents

将不同流速下立管模型CF的VIV主导频率进行无因次化，给出CF方向的平均附加质量系数与无因次频率的函数曲线，如图9所示。在图9中同时给出了半经验频域预报模型VIVANA 中的附加质量系数与无因次频率关系曲线。从图9可知，本文中立管CF方向的附加质量系数与无因次频率的关系与VIVANA给出的曲线并不相符，当无因次频率在0.13～0.16时，VIVANA中的附加质量系数为负值，大致保持为-0.6，而本文的附加质量系数大于2.5；在无因次频率0.16～0.22，VIVANA给出的附加质量系数随着无因次频率的增加迅速增大到约2.0后基本保持不变，而本文的附加质量系数在此无因次频率区间内在1.5～3.0振荡变化。

图9 立管CF方向上平均附加质量系数随无因次频率的分布Fig. 9 Distribution of the added-mass coefficient with the non-dimensional frequency in the CF direction

图10给出了立管模型IL方向的平均附加质量系数与无因次频率的函数曲线。基于刚性圆柱体纯IL方向的强迫振荡试验结果，Aronsen给出了IL方向附加质量系数与其无因次频率之间的关系曲线，如图10所示。图10显示：同一无因次频率下，本文中得到的IL方向的附加质量系数基本上大于Aronsen的值，且附加质量系数随无因次频率的变化关系也不太一致。在Aronsen给出的关系曲线中，当无因次频率从0.26增大到0.42时，附加质量系数从-0.3缓慢的增大到0.75；而在本文中，当无因次频率从0.26增大到0.32时，附加质量系数从-1.0迅速增大到1.2，而后，随着无因次频率的增大基本保持不变。

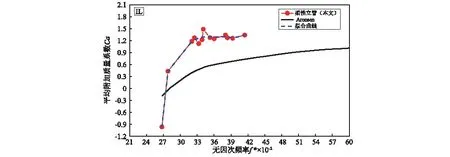
图10 立管IL方向上平均附加质量系数随无因次频率的分布Fig. 10 The distribution of the added-mass coefficient with the non-dimensional frequency in the IL direction

4 结 论

本文采用水池模型试验的方法研究了均匀流下柔性立管的涡激振动响应特性及涡激力载荷特性。文中采用FFT、小波分析法和模态分析法对均匀流场中柔性立管的VIV响应特性进行了分析，并通过欧拉-伯努利梁动态响应控制方程和最小二乘法求取了柔性立管IL和CF方向的涡激力系数。本文的主要结论如下：

(1)均匀流下柔性立管的VIV为响应幅值和主导频率不随时间变化的稳态响应，IL方向的主导频率为CF的两倍；CF方向的VIV位移大于IL方向，但两个方向的应变在同一量级。

(2)柔性立管的激励系数与圆柱体强迫振动试验获得的系数不一致：无因次频率处于激励区间的激励系数存在负值，激励系数不仅和无因次频率及振幅相关，还与CFamp;IL方向位移相位角相关。

(3)柔性立管的附加质量系数为无因次频率和VIV响应幅值的函数；但可以忽略VIV响应幅值对附加质量系数的影响，采用平均附加质量系数计算立管的固有频率。

(4)当无因次频率为0.13～0.22时，CF方向的平均附加质量系数为1.5～3.0；当无因次频率为0.26～0.42时，IL方向的平均附加质量系数从-1.0迅速增大到1.2，而后基本保持不变。

[ 1 ] MARCOLLOA H, HINWOODB J B. On shear flow single mode lock-in with both cross-flow and in-line lock-in mechanisms[J]. Journal of Fluids and Structures, 2006, 22(2): 197-211.

[ 2 ] SUMER B M, JERGEN F. Hydrodynamics around cylindrical structures[M]. Singapore: World Scientific, 2006: 334-

413.

[ 3 ] CHAPLIN J R, BEARMAN P W, FONTAINE E, et al. Blind predictions of laboratory measurements of vortex-induced vibrations of a tension riser[C]∥Fluid Induced Vibration Conference. [S. l.]: Journal of Fluids and Structures, 2005: 25-40.

[ 4 ] Design of risers for floating production systems (FPSs) and tension leg platforms (TLPs): API RP 2RD[R]. Washington: American Petroleum Institute, 1998.

[ 5 ] KAIKTSIS L, TRIANTAFYLLOU G S, ÖZBAS M. Excitation, inertia, and drag forces on a cylinder vibrating transversely to a steady flow[J]. Journal of Fluids and Structures,2007, 23(1): 1-21.

[ 6 ] SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations[J]. Journal of Fluids and Structures, 2004, 19(4): 389-447.

[ 7 ] YAMAMOTO C T, MENEGHINI J R, SALTARA F, et al. Numerical simulations of vortex-induced vibration on flexible cylinders[J]. Journal of Fluids and Structures, 2004, 19(4): 467-489.

[ 8 ] EVANGELINOS C, LUCOR D, KARNIADAKAS G E. DNS-derived force distribution on flexible cylinders subject to vortex-induced vibration[J]. Journal of Fluids and Structures, 2004, 14(3): 429-440.

[ 9 ] HUANG Z. CFD simulation of riser VIV[D]. College Station: Texas Aamp;M University, 2012.

[10] MUKUNDAN H. Vortex induced vibration and force recons-truction from field and experimental data[D]. Cambridge: Massachusetts Institute of Technology, 2008.

[11] GOPALKRISHNAN R. Vortex-induced forces on oscillating bluff cylinders[D]. Cambridge: Massachusetts Institute of Technology, 1993.

[12] HUARTE F J H, BEARMAN P W, CHAPLIN J R. On the force distribution along the axis of a flexible circular cylinder undergoing multi-mode vortex-induced vibrations[J]. Journal of Fluids and Structures,2006, 22(6/7): 897-903.

[13] WU J, LARSEN C M, KAASEN K E. A new approach for identification of forces on slender beams subjected to vortex induced vibrations[C]∥ Proceedings of Offshore Mechanics and Arctic Engineering Conference. Estoril: OMAE, 2008.

[14] WU J, MAINON P, LARSEN C M, et al. VIV force identification using classical optimal control algorithm[C]∥ Proceedings of Offshore Mechanics and Arctic Engineering Conference. Hawaii: OMAE, 2009.

[15] 陈铁云, 陈伯真. 船舶结构力学[M]. 北京：国防工业出版社, 1984: 29-30.

[16] LI L, FU S, YANG J, et al. Experimental investigation on vortex-induced vibration of risers with staggered buoyancy[C]∥ ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering. Rotterdam: OMAE, 2011.

[17] VIKESTAD K, VANDIVER J K, LARSEN C M. Added mass and oscillation frequency for circular cylinder subjected to VIV and external disturbance[J]. Journal of Fluids and Structures, 2000, 14(7): 1071-1088.

[18] FU S, REN T, LI R, et al. Experimental investigation on VIV of the flexible model within full scale Re number regime[C]∥ ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering. Rotterdam: OMAE, 2011.

[19] FANG S M, NIEDZWECKI J M, FU S, et al. VIV response of a flexible cylinder with varied coverage by buoyancy elements and helical strakes[J]. Marine Structures, 2014, 39: 70-89.

[20] VANDIVER J K, JAISWAL V, JHINGRAN V. Insights on vortex-induced, traveling waves on long risers[J]. Journal of Fluids and Structures,2009, 25(4): 641-653.

[21] LARSEN C M, YTTERVIK R, PASSANO E, et al. VIVANA theory manual[M].Trondheim: Norway, 2001.

[22] YIN D, LARSEN C M. Experimental and numerical analysis of forced motion of a circular cylinder[C]∥ Proceedings of Offshore Mechanics and Arctic Engineering Conference. Rotterdam: OM, 2011.

[23] AROSEN K H. An experimental investigation of in-line and combined in-line and cross-flow vortex induced vibrations[D]. Trondheim: NTNU, 2007.

Structuralresponsesandvortex-inducedforceofflexiblerisersundergoingvortex-inducedvibrationinuniformflow

SONG Leijian1, 2, FU Shixiao1,2, REN Tie1,2,3, YU Dapeng4, ZHANG Mengmeng1,2

(1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China;3. Marine Design amp; Research Institute of China, Shanghai 200011, China;4. Naval Academy of Armament, Beijing 100161, China)

In this study, the structural responses and vortex-induced forces of flexible risers undergoing vortex-induced vibration (VIV) in uniform flow were investigated. The VIV response characteristics were analyzed using the measured strains. Then, using the Euler Bernoulli beam structure dynamic equation and the least square method, the vortex-induced force coefficients in cross-flow (CF) and in-line (IL) direction were computed. The results indicate that the VIV of the flexible riser under uniform current is steady vibration with the amplitude and dominant frequency independent of time and the dominant frequency in the IL direction is twice as much as that in the CF direction. The excitation coefficients of the flexible riser do not always agree with those obtained by the forced oscillation tests. In the CF direction, when the non-dimensional frequency varies from 0.13 to 0.22, the added-mass coefficient oscillates between 1.5 and 3.0. In the IL direction, the added mass coefficient increases quickly from -1.0 to 1.2 and then keeps constantly when the non-dimensional frequency varies from 0.26 to 0.42.

flexible riser; vortex-induced vibration; hydrodynamic force; excitation coefficient; added-mass coefficient

国家自然科学基金资助项目(51239007； 51279101；51490674；51490675)

2016-03-29 修改稿收到日期： 2016-07-26

宋磊建 男，博士生，1987年生

付世晓 男，博士，研究员，博士生导师，1976年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.22.003