大口径高压管道物理爆炸冲击波传播规律的试验研究

程良玉， 龙 源， 毛益明， 徐全军， 纪 冲， 吴建源

(陆军工程大学 野战工程学院， 南京 210007)

大口径高压管道物理爆炸冲击波传播规律的试验研究

程良玉， 龙 源， 毛益明， 徐全军， 纪 冲， 吴建源

(陆军工程大学 野战工程学院， 南京 210007)

根据动态测试理论，构建基于DH5960的网络动态信号测试分析系统，开展直径为1 422 mm的大口径全尺寸高压气体管道爆炸试验。获取各测点空气冲击波的P(t)曲线，经小波变换滤波后采用最小二乘法对冲击波在空间上的传播特性进行数值拟合，得到了衰减曲线和衰减公式。对比试验组和对照组的冲击波曲线，发现高压管道物理爆炸空气冲击波在近地面自由场的传播具有非圆形波阵面的特征。

物理爆炸；小波变换去噪；超压衰减曲线；非圆形波阵面

天然气作为一种高效、清洁的能源为各国所青睐。未来10余年内，我国经济发展和居民对天然气的需求量仍将呈爆炸式增长。截至2015年底，我国天然气主干管道总里程达8.5万 km，已经形成相对完善的天然气管网。由于天然气管道受到近域施工行为、环境腐蚀、机械或材料失效、自然灾害及其他未知因素的影响，导致开裂爆炸事故时有发生。

天然气管道爆炸事故有两种：①物理爆炸，管道破裂后内部高压气体解除约束逸出并向自由场迅速膨胀[1]，瞬间压缩空气形成冲击波并向外传播；②化学爆炸，天然气与空气混合后，在一定外界条件作用下发生爆燃，形成化学爆炸事故。其中后者需要可燃气体在空气中扩散并受到外力作用，发生爆燃的可能性受引燃条件(如温度，混合比)的影响。而物理爆炸不需要可燃气体与氧化性气体混合，也不需要外界条件引燃。相较于天然气管道泄漏后发生的化学爆炸，物理爆炸发生的几率更高。

天然气管道泄漏后发生物理爆炸的问题一直为国内外一些专家学者所关注。Bariha等[2]理论分析了石油天然气管道发生泄漏时的气体冲击波压力场的状态；李伟等[3]采用CFD(Computer Fluid Dynamics)数值模拟计算了高压氢气输运装置物理爆炸事故后的空气冲击波状态场；Skacel等[4]通过激波管缩比试验研究了物理爆炸冲击波在管内传播规律，并验证了TNT当量法对于物理爆炸冲击波一维传播估算的可行性。这类研究通过不同的方法近似分析了物理爆炸冲击波的状态，但对于物理爆炸形成空气冲击波在自由场中传播的天然气管道全尺寸试验研究却鲜见报道。

本文基于大口径高压气体管道爆炸的全尺寸试验，获得了物理爆炸产生空气冲击波测试的数据。采用小波变换去噪方法，对物理爆炸空气冲击波在自由场的超压衰减规律及其压力场状态进行了研究。

1 试验设计与实施

1.1 高压气体管道

为研究高压天然气管道爆炸产生的空气冲击波的传播规律，开展了大口径高压气体管道爆炸的全尺寸试验。试验的管道采用X80钢材，管道长20 m，直径为1 422 mm，如图1所示。管道浅埋地下，并向管内充入一定量空气使压力升高至12 MPa，试验现场如图2所示。采用聚能切割器在管道的中心位置瞬间切割开一个50 cm的长条形切缝，管内高压气体解除约束瞬间逸出，形成物理爆炸。逸出气体到达地面上空自由场后向周围膨胀形成空气冲击波向外传播。

图1 高压气体管道中间段Fig.1 The middle section of high-pressure gas pipe

图2 高压气体管道爆炸试验现场Fig.2 The site of high-pressure gas pipe burst measuring

1.2 测点布设

为对比研究高压气体管道爆炸空气冲击波的传播规律，设置试验组和对照组两条冲击波压力测试线，分别为垂直于管道方向的垂直测试线和与管道成45°倾斜角的倾斜测试线。两条测试线各布设10个测点，共20个自由场压力测点。垂直测试线过起爆点并垂直于管道轴线，各测点距起爆点距离如表1所示；斜测试线过起爆点并沿管道东南方向，与管道轴线成45°夹角，各测点距起爆点距离如表2所示。各测点的位置示意图如图3所示。

为将压力传感器固定于近地面自由场中，避免受冲击波压力产生运动而影响测试，设计了自由场压力传感器支架。将杆式自由场传感器固定于各个对应的测点，使其距离地面1.9 m[5]。

1.3 测试系统

考虑到试验环境的特殊性，试验构建了基于DH5960的网络型动态信号测试分析系统，如图4所示。该系统采用集成的CYG411型压阻式压力传感器提高物理瞬态响应的灵敏度，并通过计算机对采集的数据进行实时存储，具有瞬态采样频率高，频率响应范围大等特点。为操作安全，设置两个采集点进行数据存储与收集，一个位于爆炸场内的测试间对数据进行直接采集，另一个位于安全范围的控制端，二者通过光纤网络联接。试验人员通过控制端计算机操控测试间计算机采集与传输试验数据，具有安全性高的特点。

表1 垂直测试线上各测点距起爆点距离

表2 斜测试线上各测点距起爆点距离

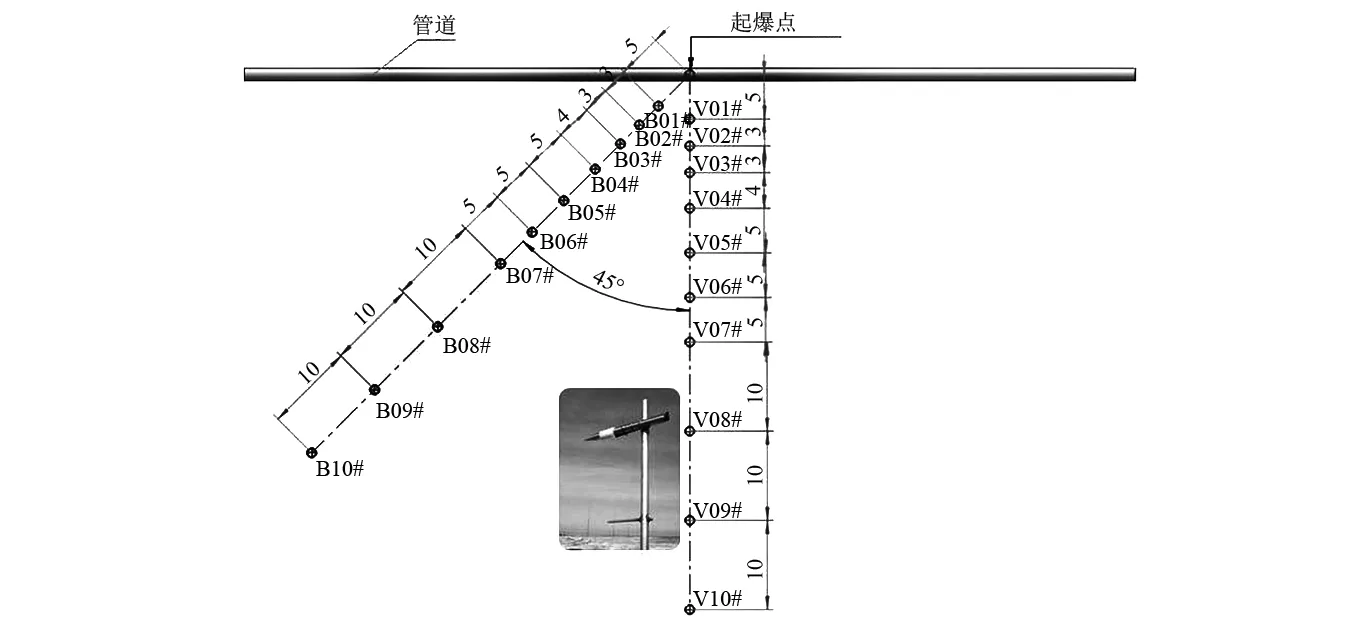
图3 测点布设示意图(单位：m)Fig.3 Schematic diagram layout of measuring point (unit: m)

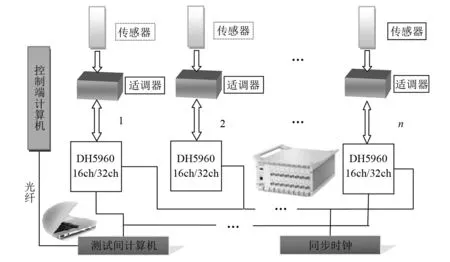
图4 DH5960动态信号测试分析系统Fig.4 DH5960 dynamic signal measurement and analysis system

2 试验结果及数据处理分析

试验共采集到20组冲击波信号。研究发现原始P(t)曲线有很多“毛刺”(噪声信号)，严重干扰有效信号的读取。通过分析发现这些噪声信号主要有两个来源：①大幅度扰动，频率范围在传感器支架固有频率附近，根据速度规律，推测为管道爆炸在土壤介质中形成的应力波扰动[6-7]。该扰动通过大地传至传感器支架底座，再通过传感器支架对传感器形成噪声干扰。这部分噪声可以通过测点布设规避，使之不出现在冲击波信号到达的时间段内，也可以通过滤波滤去。②小幅度扰动，频率范围在传感器固有频率附近，以声速在各个测点间传播，推测为冲击波形成与传播过程中对周围空气引起的扰动。该扰动通过空气介质直接对传感器形成干扰。这部分噪声无法规避，但是可以通过滤波除去。

采用小波变换对试验数据进行滤波处理[8-9]，以除去“毛刺”，获得清晰的冲击波信号，增强数据的可读性。

传感器对冲击波压力的物理响应为连续信号，但数字采集仪只能采集离散的数字信号，因此采用离散小波变换(Discrete Wavelet Transform，DWT)对原始信号进行处理。离散小波变换可通过离散化连续小波变换(Continuous Wavelet Transform，CWT)中的伸缩因子和平移因子得到[10]。离散小波为

(1)

相应的离散小波变换为

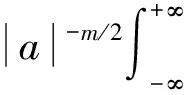
(2)

式中：ψ(t)∈L2(R);a为离散化的伸缩因子，b为离散化的平移因子，a,b∈R；m,n为离散因子，m,n∈R。

通过检验残差的收敛性，验证去噪信号与原始冲击波信号的相关性。原始P(t)曲线，去噪后的P(t)曲线和残差曲线对比如图5和图6所示。图中第一层为原始信号，第二层为去噪信号，第三层为残差曲线。

图5 垂直测线部分测点的原始曲线、滤波曲线和残差曲线Fig.5 Original signal、de-noised signal and residuals of points in vertical measuring line

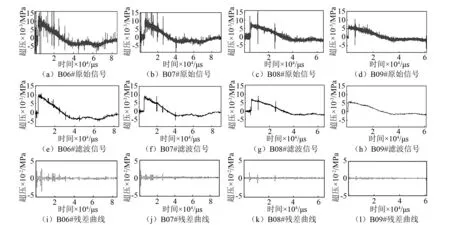
图6 倾斜测线部分测点的原始曲线、滤波曲线和残差曲线Fig.6 Original signal、de-noised signal and residuals of points in bevel measuring line

从P(t)曲线可以看出，当冲击波阵面到达测点时，压力突跃上升形成强间断面。随着气体向外膨胀压力迅速衰减，衰减至大气压力时，由于惯性作用继续下降形成一个压力稍小于大气压力的负压区。负压区被周围高压区压缩，压力升高至稍高于大气压力。接着又开始第二次膨胀和压缩的脉动过程。通过多次有阻尼脉动，压力衰减至大气压力；并且同一条测线上距离越远的测点所测到的超压峰值越小，衰减速度越慢。这与常规爆炸冲击波的传播规律类似。

从残差曲线图中可以看出，时域范围内，残差一直在零点附近波动，其主值基本收敛于直线P=0，说明小波变换去噪没有改变原始信号的冲击突跃部分，去噪结果清晰可靠。将读取的冲击波数据列于表3和表4(其中B05#测点未测到有效信息)。

表3 垂直测试线上各测点超压峰值

表4 斜测试线上各测点超压峰值

3 冲击波传播特性分析

3.1 超压衰减曲线拟合

空气冲击波在自由场中传播具有气体压力大，传播速度快等特点，此过程中气体的重力和黏性可忽略不计，气体可以假定为完全气体[11]，根据相似理论有

Δpm=f(E,r,P0,ρ0,k)

(3)

式中：被定量ΔPm为冲击波超压；主定量E为爆炸总能量；r为冲击波波阵面距爆心距离；P0为空气的初始压力；ρ0为空气的初始密度；k为绝热指数。

由π定理写出三个π项

(4)

根据量纲和谐条件求解得到

(5)

k一般取常数，P0一定的条件下，式(5)可写成

(6)

将式(6)展开

(7)

爆炸能量由管内气体唯一确定，冲击波传播过程中E不发生改变，可当作常量，则式(7)变为

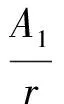
(8)

已知边界条件：当r→∞时，ΔPm=0，故A0=0，则

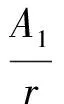
(9)

结合试验数据，采用最小二乘法分别对两条测线上的超压进行曲线拟合，获得拟合曲线和拟合函数，拟合曲线如图7和图8所示。

图7 Vertical测线的拟合曲线Fig.7 Fitting curve of vertical measuring line

图8 斜测线的拟合曲线Fig.8 Fitting curve of bevel measuring line

垂直方向的超压衰减拟合函数

(10)

45°角倾斜方向的超压衰减函数

(11)

3.2 冲击波阵面的非圆形特征

研究试验组与对照组的冲击波超压发现，相同距离时垂直测线上测点超压明显高于倾斜测线上对应测点的超压，即截取相同超压时，垂直测线上的距离比斜测线上的距离更远。说明在近地面自由场中空气冲击波超压的等压线为非圆形，如图9所示。冲击波阵面为压力最大的等压线，在近点面自由场中的分布也具有非圆形的特征。

图9 冲击波等压线Fig.9 Shockwave isobars schematic diagram

分析发现，非圆形波阵面的形成与管道破裂气体逸出及冲击波传播过程有关。如图10所示，切割器沿管道轴线切开一个长条形切缝。切缝轴向尺寸大于径向尺寸，即径向自由面大于轴向自由面，致使其径向强度小于轴向强度。在内部高压作用下，切缝先从中间位置沿径向发生塑性变形，撕裂成裂口如图11所示。由于径向塑性变形程度更大，气体从裂口逸出时，径向泄漏更快，更早形成冲击波，导致初始波阵面为非圆形波阵面。

各方面非均匀的空气冲击波在传播过程中有一个各方面渐近均匀化作用[12]，将非圆形波阵面均匀化为近似圆形的波阵面。化学爆炸形成的空气冲击波超压一般很大，因此各方面渐近均匀化作用很明显，很快形成近似圆形的冲击波阵面；而管道爆炸空气冲击波超压较小，各方面渐近均匀化作用不明显，因此在近地面自由场中具有明显的非圆形波阵面特征。

图10 爆炸切缝Fig.10 Blasting incision

图11 裂口变形及气体喷流示意图Fig.11 Crack deformation and gas jet schematic diagram

4 结 论

(1)冲击波测试过程中干扰信号主要有两部分：①管道爆炸在土壤介质中形成的应力波扰动；②冲击波在周围空气中形成的不规则扰动，这两部分噪声都与传感器和支架的固有频率有关。

(2)根据试验数据，拟合得到本试验物理爆炸空气冲击波在与管道垂直方向和与管道成45°角方向上的超压衰减曲线及其函数。可以为实际应用提供有效参考。

(3)高压气体管道物理爆炸形成空气冲击波，其波阵面形状受管道破裂变形过程和冲击波传播过程双重影响而具有非圆形特征，如本次试验所得的冲击波传播呈现与管道垂直方向最强，其他方向稍弱的非圆形波阵面特征。说明高压管道爆炸形成空气冲击波的安全防护不同方向具有不同的防护等级。

[ 1 ] STAWCZYK J. Experimental evaluation of LPG tank explosion hazards[J]. Journal of Hazardous Materials，2003，96 (2/3)：189-200.

[ 2 ] BARIHA N，MISHRA I M，SRIVASTAVA V C. Hazard analysis of failure of natural gas and petroleum gas pipelines[J]. Journal of Loss Prevention in the Process Industries ，2016，40： 217-226.

[ 3 ] 李伟，张奇. 高压氢气输运装置物理爆炸状态场特征及灾害效应研究[J]. 高压物理学报，2009，23(3)：203-208.LI Wei，ZHANG Qi. Study on the physical explosion character and ejection effect of the high-pressurized hydrogen transport device[J]. Chinese Journal of High Pressure Physics，2009，23(3)：203-208.

[ 4 ] SKACEL R，JANOVSKY B，DOSTAL L，et al. Small-scale physical explosions in shock tubes in comparison with condensed high explosive detonations[J]. Journal of Loss Prevention in the Process Industries，2013，26(6)：1590-1596.

[ 5 ] 杜红棉，祖静，马铁华，等. 自由场传感器外形结构对冲击波测试的影响研究[J]. 振动与冲击，2011,30(11)：85-89.

DU Hongmian，ZU Jing，MA Tiehua，et al. Effect of mount configuration of free-field transducers on shock wave measurement[J]. Journal of Vibration and Shock，2011,30(11)：85-89.

[ 6 ] 张志镇，高峰，林斌，等. 岩石冲击倾向与其波速变化的相关性研究[J]. 岩石力学与工程学报，2012，31(2)：3527-3532.

ZHANG Zhizhen，GAO Feng，LIN Bin，et al. Correlation study of rock burst tendency and ultrasonic velocity[J]. Chinese Journal of Rock Mechanics and Engineering，2012，31(2): 3527-3532.

[ 7 ] 邱志刚，薄景山，罗奇峰. 土壤剪切波速与埋深关系的统计分析[J]. 世界地震工程，2011，27(3): 81-88.

QIU Zhigang，BO Jingshan，LUO Qifeng. Statistical analysis of relationship between shear wave velocity and depth of soil[J]. World Earthquake Engineering，2011，27(3): 81-88.

[ 8 ] 贾云飞,张春棋,康金. 爆炸冲击波信号测试与小波分析[J]. 弹箭与制导学报，2014，34(5): 86-89.

JIA Yunfei，ZHANG Chunqi，KANG Jin. Shock wave signal measuring and wavelet analysis [J]. Journal of Projectiles，Rockets，Missiles and Guidance, 2014, 34(5): 86-89.

[ 9 ] 张衍芳. 冲击波信号处理方法的研究[D].太原：中北大学,2011.

[10] 张德丰. MATLAB小波分析[M].北京：机械工业出版社，2009.

[11] 郑哲敏，谈庆明，王补宣. 相似理论与模化[C]∥ 郑哲敏文集. 北京：科学出版社，2004: 777-808.

[12] 奥尔连科. 爆炸物理学[M]. 孙承纬, 译. 北京：科学出版社，2011.

Anexperimentalstudyonlarge-diameterhigh-pressurepipelinephysicalexplosionsshockwavepropagation

CHENG Liangyu, LONG Yuan，MAO Yiming，XU Quanjun，JI Chong，WU Jianyuan

(College of Field Engineering，Army Engineering University, Nanjing 210007, China)

According to the theory of dynamic test, this paper presented a DH5960-based dynamic signal analysis system, in which a diameter of 1 422 mm full-size high-pressure gas pipeline explosion experiments was performed. The air blast curve of each measuring point was obtained. After the wavelet de-noising, the least squares method was adopted to carry out numerical fitting of the peak overpressure shock wave propagation characteristics in space. Decay curves and attenuation formula were obtained. Shock curve comparison between experimental group and the control group were performed and discovered that high-pressure pipeline physics explosion air shock has the feature of a noncircular wave front propagation characteristics on the free-field near the ground.

physical explosions; wavelet de-noising; overpressure decay curve; noncircular wave front

国家自然科学基金(11672331)；中国博士后科学基金(2015M58279)

2016-06-24 修改稿收到日期： 2016-07-22

程良玉 男，硕士生，1992年生

龙源 男，博士，教授，博士生导师，1958年生

O383； X937

A

10.13465/j.cnki.jvs.2017.22.007