超临界轴向运动Timoshenko梁横向受迫振动
2017-11-30陈立群
谭 霞, 丁 虎, 陈立群,2
(1.上海大学 上海市应用数学和力学研究所, 上海 200072; 2.上海大学 理学院,上海 200444)
超临界轴向运动Timoshenko梁横向受迫振动
谭 霞1, 丁 虎1, 陈立群1,2
(1.上海大学 上海市应用数学和力学研究所, 上海 200072; 2.上海大学 理学院,上海 200444)
研究外部激励作用下,超临界轴向运动Timoshenko梁横向非线性振动的稳态响应。通过对非零平衡位形的坐标变换,从轴向运动Timoshenko梁的横向振动控制方程推导得到超临界速度下受横向外部激励的陀螺系统标准控制方程。运用Galerkin截断法数值研究超临界下轴向运动Timoshenko梁的稳态周期幅频响应关系,并通过与超临界速度下轴向运动Euler-Bernoulli梁的稳态幅频响应曲线进行对比,研究Euler-Bernoulli梁理论的适用范围。
超临界;轴向运动梁;Timoshenko理论;受迫振动;Galerkin截断法
工程实际及生活中随处可见轴向运动梁结构,如机床传动带、观光缆车、机械传送带、发动机等带传动系统,通常都可简化为轴向运动梁模型。轴向运动梁作为最基本最典型的陀螺连续系统,其振动分析与控制有着重要的理论研究意义。一系列优秀的综述反映了轴向运动体系的研究意义和研究成果[1-4]。
国内外学者对亚临界速度下轴向运动体系已经有了比较系统的研究。宫苏梅等[5]对于平带系统的相关非线性振动进行了实验研究。吕海炜等[6]对轴向运动软夹层梁横向振动进行了分析研究。丁虎等[7-8]研究了轴向运动黏弹性梁的横向非线性受迫振动,运用有限差分法研究了轴向运动梁非线性振动的固有频率。Ghayesh等[9]研究了转动惯量和温度对轴向运动梁的非线性振动、稳态响应和稳定性的影响。随着研究的深入和科技发展的要求,众多学者越来越关注轴向运动系统高速运动状态下的相关动力学特性。Huang等[10]研究分析了超临界速度下轴向稳定运动梁的稳定性。Ding等[11]运用Galerkin截断法研究得到了高速轴向运动梁的固有频率。以上研究高速轴向运动体系的文献都是运用的E-B(Euler-Bernoulli)梁理论,没有考虑剪切力和转动惯量的影响。相对而言,对于Timoshenko梁的研究很少,高速轴向运动的Timoshenko梁理论研究就更加少见了。Tang等[12-13]研究了亚临界下强弱外载荷作用下轴向运动黏弹性Timoshenko梁的非线性振动,以及参数和外载荷作用下Timoshenko梁的非线性动力学特性。他们的研究发现,在一定参数条件下,E-B梁理论和Timoshenko梁会产生显著差别。
本文运用Galerkin截断法研究了超临界轴向运动Timoshenko梁横向受迫振动的稳态响应。并与超临界速度下的E-B梁稳态响应进行了对比,进一步研究两种梁理论间的异同,确定E-B梁理论在超临界运动范围内的适用范围。
1 数学模型和控制方程
图1为超临界轴向运动Timoshenko梁的物理模型。其中ρ为质量密度;A为横截面面积;E为弹性模量;EI为梁的弯曲刚度;G为剪切模量;I为关于中性轴的截面惯性矩;轴向坐标X为离开左边界的距离;V(X,T) 为横向位移;T为是时间坐标;P0为梁的初始轴向张力。 此外,梁以固定速度Γ轴向运动,梁长为L。
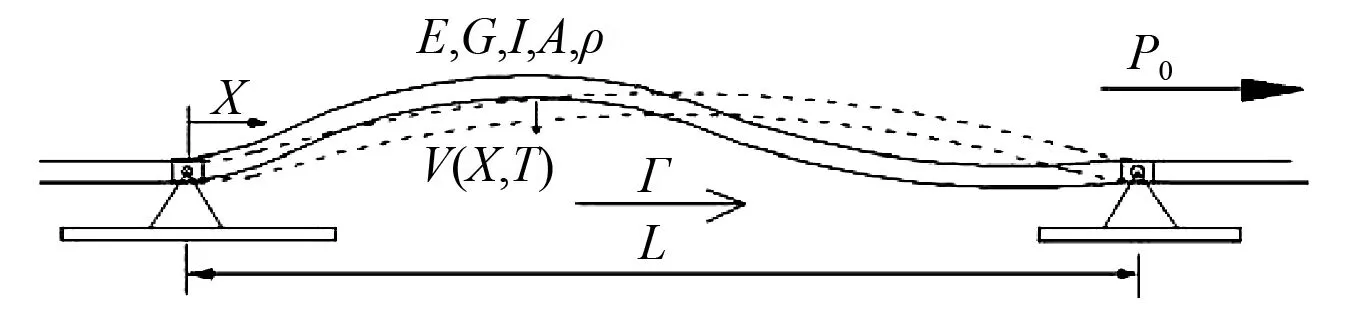
图1 轴向运动梁物理模型Fig.1 The physical model of an axially moving beam
根据广义的哈密顿原理和Timoshenko梁理论,建立轴向运动梁的无量纲运动方程[14-15]
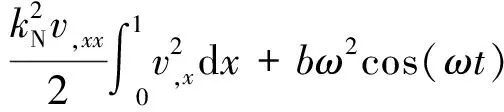
(1)
其中无量纲变量x,t和v(x,t)定义为

(2)
φ(x,t)为弯矩产生的Timoshenko梁轴线的转角。变量前的逗号表示求偏导。无量纲参数定义为
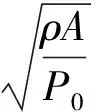
(3)
式中:κ为形状因子;无量纲参数k1,k2,kN,kf分别为剪切变形系数,转动惯量系数,非线性系数和刚度系数;ks为轴向支撑刚度参数。
无量纲简支边界条件为

(4)
由于非平凡静平衡位形与时间项无关,因此忽略时间项得到静态控制方程和静态简支边界条件
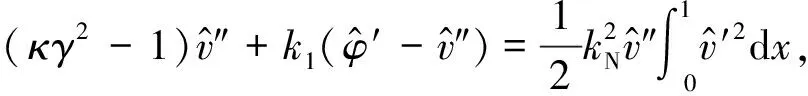
(5)
推导得到简支边界下超临界下轴向运动Timoshenko梁的第一阶非平凡静平衡位形
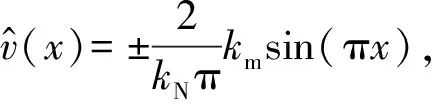
(6)

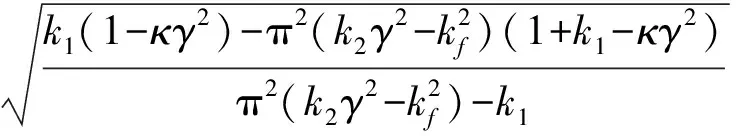
(7)
2 Galerkin截断
对方程式(1)进行坐标代换,且只考虑第一阶正非平凡静平衡位形,得到
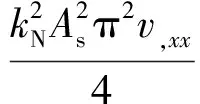
(8)
其中,

(9)
为满足两端简支边界条件,取式(7)形式解[16]如下
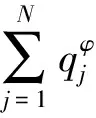
(10)
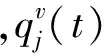

(11)
在式(11)等号的左右两边分别乘以权函数sin(iπx),cos(iπx),i=1,2,…,N,并在区间[0,1]上积分,得到常微分方程组
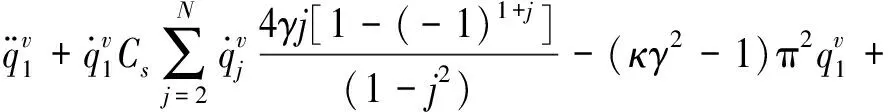
(12)
3 稳态响应
运用Galerkin截断法数值研究了应用于工程实际中的V型传动带。
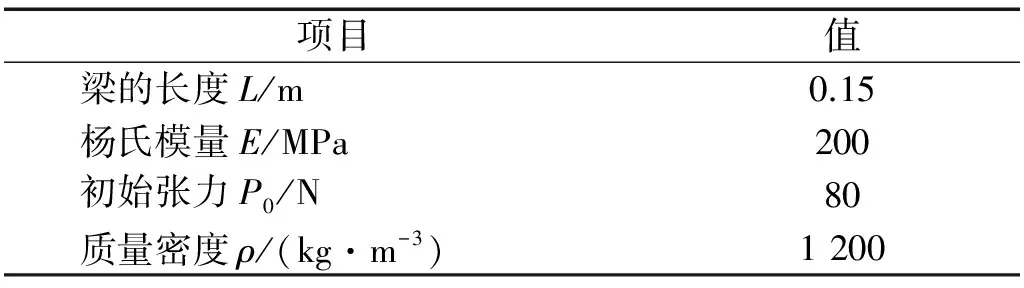
表1 V带的物理参数
V带上底宽为 0.022 m,高为0.018 m,楔角为40°。形状因子为6/5。外阻尼Cs=0.1。相应的无量纲参kf=0.885 6,kN=26.366 3,k1=281.831 4,k2=0.001 1。计算得到简支边界下超临界轴向运动Timoshenko梁的无量纲临界速度γ=3,相应的物理速度Γ=46.45 m/s。
考虑N=4时的Galerkin截断,γ=4,激励幅值b=0.000 2,运用四阶龙格-库塔法计算激励频率接近系统第一阶固有频率时,式(12)的响应。仿真中,时间步长取0.01 s,初始条件取为0。在计算所得的前500 s的时间历程中,取最后5 s计算Timoshenko梁的稳态幅频响应[17]。
如图2所示为超临界轴向运动Timoshenko梁横向受迫振动前500 s的时间历程。

图2 横向受迫振动时域响应(ω=9.25)Fig.2 Time-domain response of lateral forced vibration
考虑四阶Galerkin截断计算梁中点的稳态振幅,研究第一阶主谐波共振时的稳态响应。图3~图5分别给出了剪切变形系数、转动惯量系数和外阻尼对第一阶主谐波共振时稳态幅频特性曲线的影响。图3表明共振幅度随剪切变形系数的增大而增大,幅频特性曲线向左偏,呈现软特性,且随着剪切系数的增大,软特性增强。图4表明共振幅度随剪切变形系数的增大而减小,软特性减弱。图5表明共振幅度随外阻尼的增大而减小,软特性减弱。
4 与Euler-Bernoulli梁理论对比
超临界轴向运动Euler-Bernoulli梁横向受迫振动控制方程

(13)
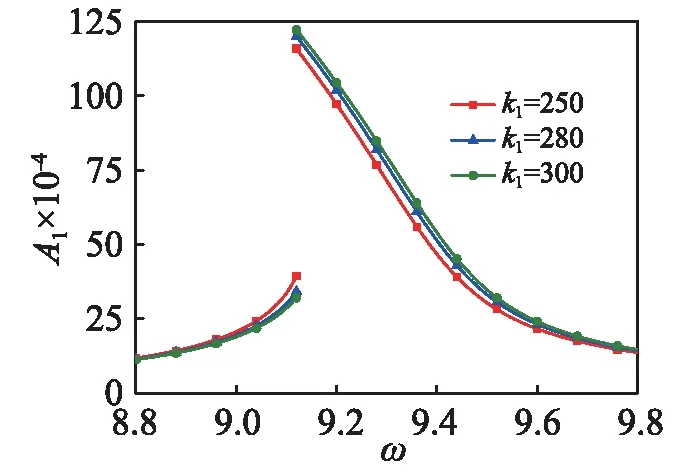
图3 剪切变形系数对稳态幅频特性曲线的影响Fig.3 Effects of shear deformation coefficient of amplitude frequency response
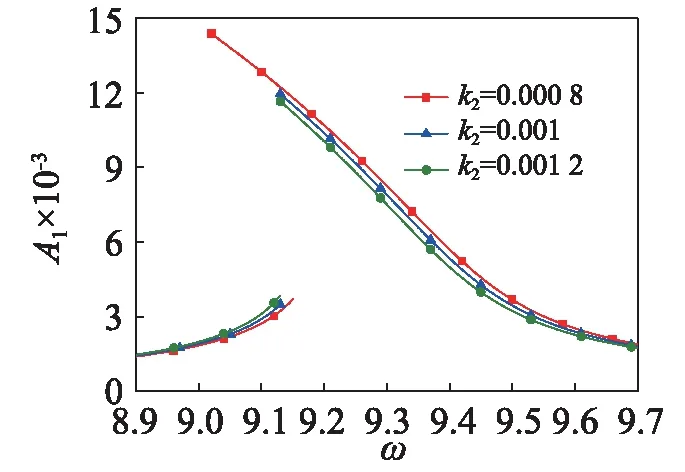
图4 转动惯量系数对稳态幅频特性曲线的影响Fig.4 Effects of rotary inertia coefficient of amplitude frequency response
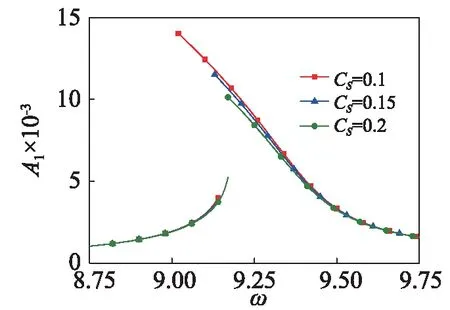
图5 外部阻尼对稳态幅频特性曲线的影响Fig.5 Effects of external damping of amplitude frequency response
简支边界下E-B梁第一阶非平凡静平衡位形
(14)
对式(12)进行坐标代换,且只考虑E-B梁的第一阶正非平凡静平衡位形,得到
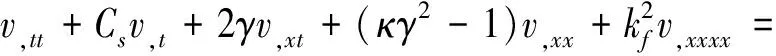
(15)
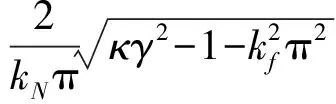
(16)
为满足两端简支边界条件,取式(17)为式(14)的形式解
(17)
将式(16)代入式(14)后,在方程两边同乘以权函数sin(iπx),i=1,2,…,N,并在区间[0,1]上积分,得到常微分方程组
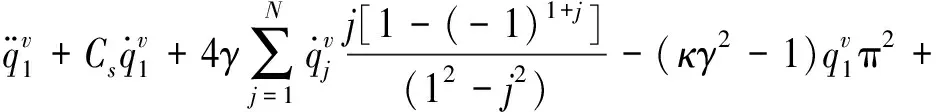

(18)
图6和图7分别给出了不同梁模型下梁长和梁横截面高度对稳态响应幅频特性曲线的影响。
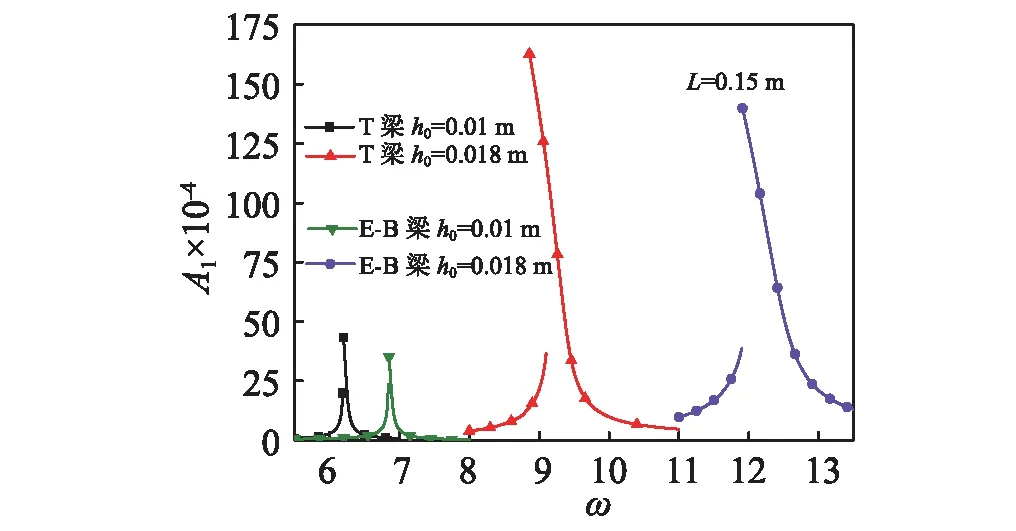
图6 梁横截面高度对稳态幅频特性曲线的影响Fig.6 Effects of beam cross section height of amplitude frequency response
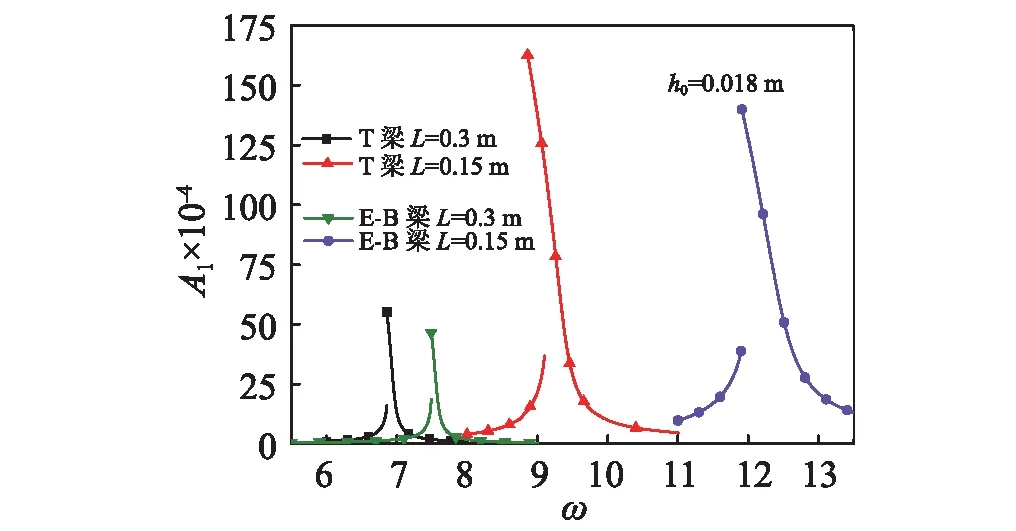
图7 梁长对稳态幅频特性曲线的影响Fig.7 Effects of beam length of amplitude frequency response
图6中考虑了两种梁模型横截面高分别为0.01 m和0.018 m时的稳态响应幅频特性曲线,从图6可知,两种梁模型的共振频率差别较大,共振幅度也有较大差别。图7考虑了两种梁模型梁长分别为0.15 m和0.3 m时的稳态响应幅频特性曲线,同样,两种梁模型的共振频率差别较大,共振幅度也有较大差别。从图6和图7可知,当L与h0的比值变大时,两种梁模型之间的差别变小。
5 结 论
本文运用Galerkin截断法数值研究了有外阻尼的超临界轴向运动Timoshenko梁的横向受迫振动,得到了Timoshenko梁稳态周期幅频特性曲线,并考虑了相关参数对其的影响。
同时对比了Timoshenko和Euler-Bernoulli这两种梁模型在超临界轴向速度下的稳态幅频特性曲线,发现两种梁模型的幅频特性曲线存在较大差别,当梁的截面高度变大时,两种梁模型的稳态幅频特性曲线差别变大,当梁长变大时,两种梁模型的稳态幅频特性曲线差别变小。
[ 1 ] WICKET J A, MOTE C D. Classical vibration analysis of axially moving continua [J]. ASME Journal of Applied Mechanics, 1990, 57 (3): 738-744.
[ 2 ] ZHU W D. Vibration and stability of time-dependent of translating media [J]. Shock and Vibration Digest, 2000, 32 (5): 369-379.
[ 3 ] CHEN L Q. Analysis and control of transverse vibration of axially moving strings [J]. ASME Applied Mechanics Reviews, 2005, 58 (2): 91-116.
[ 4 ] MARYNOWSKI K, KAPITANIAK T. Dynamics of axially moving continua [J]. International Journal of Mechanical Sciences, 2014,81(4): 26-41.
[ 5 ] 宫苏梅, 张伟. 平带系统非线性振动实验研究[J]. 动力学与控制学报, 2014, 12(4): 368-372.
GONG Sumei, ZHANG Wei. Experimental study on nonlinear vibration of flat-belt system[J]. Journal of Dynamics and Control, 2014, 12(4): 368-372.
[ 6 ] 吕海炜, 李映辉, 李亮, 等. 轴向运动软夹层梁横向振动分析[J]. 振动与冲击, 2014, 33(2): 41-51.
LÜ Haiwei, LI Yinghui, LI Liang, et al. Analysis of transverse vibration of axially moving soft sandwich beam[J]. Journal of Vibration and Shock, 2014, 33(2): 41-51.
[ 7 ] 丁虎, 陈立群. 轴向运动黏弹性梁横向非线性受迫振动[J]. 振动与冲击, 2009, 28(12): 128-131.
DING Hu, CHEN Liqun. Transverse non-linear forced vibration of axially moving viscoelastic beam[J]. Journal of Vibration and Shock, 2009, 28(12): 128-131.
[ 8 ] DING H, CHEN L Q. Natural frequencies of nonlinear vibration of axially moving beams[J]. Nonlinear Dynamics, 2011, 63(1/2): 125-134.
[ 9 ] GHAYESH M H, KHADEM S E. Rotary inertia and temperature effects on non-linear vibration, steady-state response and stability of an axially moving beam with time-dependent velocity [J]. International Journal of Mechanical Science, 2008, 50 (3): 389-404.
[10] HUANG S J, PERKINS N C. Supercritical stability of an axially moving beam. Part Ⅱ: vibration and stability analyses [J]. Journal of Sound and Vibration, 1992, 154 (3): 397-409.
[11] DING H, CHEN L Q. Galerkin methods for natural frequencies of high-speed axially moving beams [J]. Journal of Sound and Vibration, 2001, 329 (17): 3484-3494.
[12] TANG Y Q, CHEN L Q, YANG X D. Non-linear vibrations of axially moving Timoshenko beams under weak and strong external excitations [J]. Journal of Sound and Vibration, 2009, 320 (4/5): 1078-1099.
[13] YAN Qiaoyun, DING Hu, CHEN Liqun. Nonlinear dynamics of an axially moving viscoelastic Timoshenko beam under parametric and external excitations[J].Applied Mathematics and Mechanics (English Edition), 2015, 36(8): 971-984.
[14] DING H, JEAN W Z. Effect of one-way clutch on the nonlinear vibration of belt-drive systems with a continuous belt model[J]. Journal of Sound and Vibration, 2013, 332(24): 6472-6487.
[15] YAN Q Y, DING H, CHEN L Q. Periodic responses and chaos behaviors of an axially accelerating viscoelastic Timoshenko beam[J]. Non-linear Dynamics, 2014, 78(2):1577-1591.
[16] CHEN S H, HUANG J L, SZE K Y. Multidimensional Lindstedt-Poincaré method for nonlinear vibration of axially moving beams[J]. Journal of Sound and Vibration, 2007, 306(1/2): 1-11.
[17] 李大鹏, 储德林, 丁虎. 轮-带驱动系统稳态周期响应谐波平衡分析[J]. 动力学与控制学报, 2015, 13(6): 423-429.
LI Dapeng, CHU Delin, DING Hu. The frequency-response curve of a belt-drive system by using the harmonic balance method[J]. Journal of Dynamics and Control, 2015, 13(6): 423-429.
TransverseforcedvibrationofanaxiallymovingTimoshenkobeamatasupercriticalspeed
TAN Xia1, DING Hu1, CHEN Liqun1,2
(1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China;2.College of Sciences, Shanghai University, Shanghai 200444, China)
In this paper, the transverse nonlinear forced vibration of an axially moving Timoshenko beam at a supercritical speed was studied under external excitation. In the supercritical region, the standard control equation of the gyro system, under the lateral external incentives, was derived based on the governing equation of transverse nonlinear vibration of the axially moving Timoshenko beam. Moreover, the steady-state amplitude frequency response relationship of the axially moving Timoshenko beam at a supercritical speed was investigated by using the Galerkin method. Furthermore, the effects of system parameters on the steady-state amplitude frequency response relationship of the Timoshenko beam were considered. Comparisons with Euler-Bernoulli (E-B) beam reveal that the resonance frequency of the Timoshenko beam is much lower and the resonance amplitude is higher in the supercritical region.
supercritical; axially moving beam; Timoshenko theory; forced vibration; Galerkin method
国家自然科学基金重点项目(11232009); 国家自然科学基金项目(11372171; 11422214)
2016-06-02 修改稿收到日期: 2016-09-28
谭霞 女,硕士生,1992年生
丁虎 男,博士,教授,博士生导师,1978年生
E-mail: dinghu3@shu.edu.cn
O322
A
10.13465/j.cnki.jvs.2017.22.001
