考虑质量偏心的阶梯梁-基础的强迫振动计算

王 剑， 张振果， 任龙龙， 华宏星

(1. 上海交通大学 振动、冲击、噪声研究所，上海 200240；2. 上海交通大学 机械系统与振动国家重点实验室，上海 200240)

考虑质量偏心的阶梯梁-基础的强迫振动计算

王 剑1,2， 张振果1,2， 任龙龙1,2， 华宏星1,2

(1. 上海交通大学 振动、冲击、噪声研究所，上海 200240；2. 上海交通大学 机械系统与振动国家重点实验室，上海 200240)

轴系的质量非均匀会导致纵横振动的耦合，结合导纳综合法与改进的传递矩阵法，针对质量偏心阶梯梁-弹性基础模型，提出了一种理论/实验混合计算方法。通过与有限元计算结果对比，验证了方法的正确性；考察了质量偏心对系统响应的影响。结果表明：在垂向激励下，质量偏心对系统的垂向位移响应无影响，但是会使系统产生纵向位移响应；由于纵向位移以eθ的形式被引入弯-纵耦合振动方程，因此其频率特征与垂向响应一致，且其幅值与偏心程度成正比。

质量偏心； 阶梯梁； 弹性基础； 导纳综合法

作为轴系的物理简化模型，阶梯梁的动力学问题引起了大量学者的关注[1-4]。实际中，由于加工或安装的原因，轴系一般会存在质量偏心(质心与截面形心不重合)，从而导致垂向振动与纵向振动的耦合[5]。壳体n=0 (n为壳体的周向波数)的模态拥有较高的声辐射效率[6]，轴系的纵向振动导致的纵向力传递至壳体会引发较大的声辐射[7]，因此很有必要对质量偏心引起的轴系纵横耦合振动进行研究。王剑等给出了考虑质量偏心Timoshenko梁的弯(垂直)-纵耦合振动控制方程，但未涉及强迫响应。

梁结构一般安装在弹性基础上，近年来，国内外学者对此梁-弹性基础耦合系统的振动问题展开了一系列工作。对于梁-弹性基础的建模，常用的方法[8]有阻抗综合法、有限元法和传递矩阵法。Bonello等[9]基于阻抗综合法，对阶梯梁-基础模型的振动进行了研究，该建模方法的优势在于可以将理论与实验结果结合起来描述系统，但其求解矩阵的维数与梁结构的支撑数目成正比。有限元法在基础比较复杂的情况下通常要耗费较大的资源[10]。传递矩阵法[11]只适用于链式结构，不能将复杂弹性基础有效地考虑在内。

Zhang等[12]利用改进的传递矩阵法，建立了非连续(截面突变，集中质量块，连接弹簧等)Timoshenko双梁模型的动力学模型，这种方法可以使求解矩阵的维数与梁控制方程的阶数保持一致，具有较高的求解效率。本文结合改进的传递矩阵法与导纳综合法，建立了质量偏心阶梯梁-基础的振动模型。通过与有限元软件ANSYS计算结果的对比，验证了方法的正确性。并考察了质量偏心对系统弯-纵耦合振动的影响，解释了其产生的原因。相较于前人提出的建模方法，本文的方法可以使相关矩阵的维数保持在6×6，有利于提高计算效率。另外，每一个子梁段的特征以矩阵相乘的形如引入，提高了程序编写的便利性。

1 偏心阶梯梁-基础模型

1.1 考虑质量偏心的Timoshenko梁运动方程

考虑质量偏心Timoshenko梁的弯-纵耦合振动方程为

(1)

(2)

(3)

式中：ρ为梁的密度；A为梁的截面面积；u为梁的纵向位移；E为材料的弹性模量；θ为转动角度；v为梁的横向位移；k为剪切因子；I为梁截面的截面惯性矩；e为梁质心和形心之间的距离， 见图1所示；Q为剪切力；N为轴向力；M为弯矩；D为形心(刚度中心、弯曲中心)；G为质量中心；γ为剪切应变。

图1 质心和几何中心不重合的Timoshenko梁微元Fig.1 Timoshenko beam element with misalignment between centroid and geometric center

内力与位移的关系为

(4)

利用分离变量法[13]，将三个位移写成关于空间和时间函数的乘积

u(x,t)=U(x)eiωt

(5)

v(x,t)=V(x)eiωt

(6)

θ(x,t)=Θ(x)eiωt

(7)

进一步将空间项写作指数函数

U(x)=Beλx;V(x)=Ceλx;Θ(x)=Deλx

(8)

将式(5)～式(8)代入式(1)～式(3)并消去时间项,为使系数B、C、D有非零解，可得特征方程

kGE2Iλ6+Eρω2(2kGI+2kGAe2+EI)λ4+
ρω2(-kGEA+2EAe2ρω2+2EIρω2+
kGIρω2+kGAe2ρω2)λ2+
ρ2ω4(-kGA+Iρω2+Ae2ρω2)=0

(9)

解出特征值λ1,λ2, …,λ6，位移就可以写为矩阵形式

U(x)=eλxB;V(x)=eλxC;Θ(x)=eλxD

(10)

其中，

eλx=[eλ1xeλ2xeλ3xeλ4xeλ5xeλ6x]
B=[B1B2B3B4B5B6]T
C=[C1C2C3C4C5C6]T
D=[D1D2D3D4D5D6]T

根据式(1)～式(3)，系数C、D与B的关系为

C=HB;D=SB

(11)

其中，

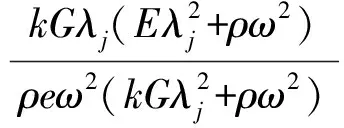
1.2 偏心阶梯梁-基础模型

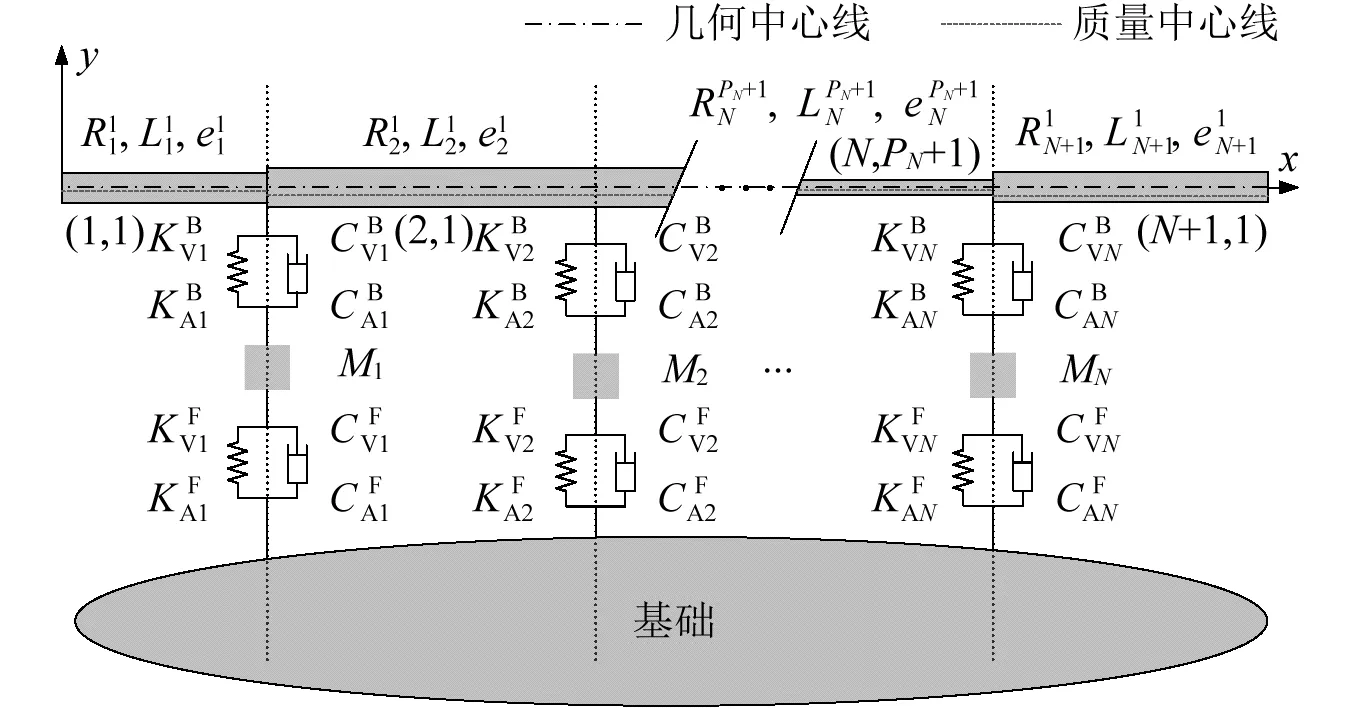
图2 偏心阶梯梁-基础模型示意图Fig.2 Illustration of the eccentric stepped beam-foundation

2 耦合振动求解

2.1 梁段间的系数传递关系

考虑第n个弹簧处梁段间位移系数的传递，界面处的受力分析图如图3所示。

图3 梁段间受力分析图Fig.3 Illustration of the force compatibility conditions

位移连续条件为

(12)

(13)

(14)

力平衡条件为

(15)

(16)

(17)

将式(10)代入式(12)～式(17)并写成矩阵形式

(18)

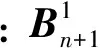
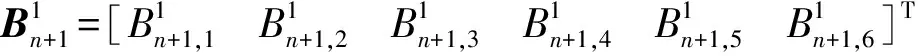
2.2 梁段内的系数传递关系

假设第n-1～第n个弹簧支撑之间的梁有Pn个截面突变。类似地，将位移代入突变处的位移连续及力平衡条件，并写成矩阵形式

(19)

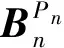
因此，第(n,Pn+1)梁段与(n,1)梁段纵向振动的振型系数关系为

(20)

式(18)可表示为

(21)

2.3 梁与基础的综合

(22)

其中，

作用在基础上的反力可以用基础与中间质量块的相对位移表示

(23)

同理，梁上的反力可以表示为

(24)

其中,

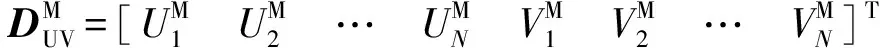
对于弹簧系统中的N个质量块，给出其运动方程

(25)

即

(26)

将式(23)、式(24)代入式(26)整理得

(27)

式中，KM=KF+KB+ω2M。

通过式(22)与式(23)可得

(28)

考虑式(27)、式(28)有

(29)

将式(29)代入式(24)可得

(30)

式中，ZB如下(里面的I为2N×2N的单位矩阵)

将式(30)中梁的阻抗矩阵拆解为列向量的叠加

(31)

结合式(31)，式(21)可以表示为

(32)

式中，Wmn如下(里面0为1×6的零向量)

式中，n的值从1～N，并写为矩阵形式， 其中，0为6×1的零向量。

(33)

式中，TR、TW如下(里面的I为6×6的单位矩阵)

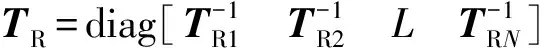
记为

(34)

由式(34)可得

(35)

在梁的首尾两端引入自由边界条件

(36)

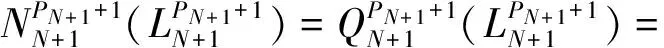
(37)

将内力表达式代入式(36)、式(37)并写为矩阵形式

(38)

(39)

将式(35)代入式(39)并与式(38)合写为

(40)

2.4 强迫响应计算

如果简谐激励施加在梁的端部，可将其引入边界条件式(38)、式(39)，将式(40)改写为

(41)

式中，F=[NLQLMLNRQRMR]T，NL、QL、ML为施加在左端处三种载荷的幅值，NR、QR、MR为施加在右端处三种载荷的幅值。

如果简谐激励施加在梁非端点处的任意位置，可在载荷施加处将梁分段，以力平衡的方式将外载荷引入系数传递关系。

求解式(41)，进一步得到各梁子段的位移系数后，可得到梁上的响应。据式(24)、式(28)、式(31)，可求得基础上与梁连接处的响应。

3 算法验证

为了验证本文方法的有效性，建立阶梯梁-圆柱壳模型作为验证算例。模型中阶梯梁未考虑质量偏心，两端均为自由边界条件，圆柱壳两端的边界条件为薄膜简支边界。梁与圆柱壳由三组弹簧连接，在梁的左端施加一个简谐垂向激励，幅值F0=1 N，取图4中所示，点1与点2的响应结果与有限元作对比，点2距圆柱壳左端的距离为0.1 m。ANSYS中梁采用Beam188单元，单元尺寸为0.01 m；圆柱壳采用Shell163单元，尺寸为0.1 m。模型的具体参数见表1，其中μ为泊松比，剪切因子k的取值参照文献[14]。模型中纵向刚度、阻尼及质量块的值均为零。

表2对比了两种方法下系统的前十阶固有频率，各阶的相对误差均在0.05%之内。由于圆柱壳存在对称模态与反对称模态[15]，因此计算结果以两个相近频率为一组的形式出现。

图4 验证模型示意图Fig.4 Schematic of the validation model

表1 验证模型参数

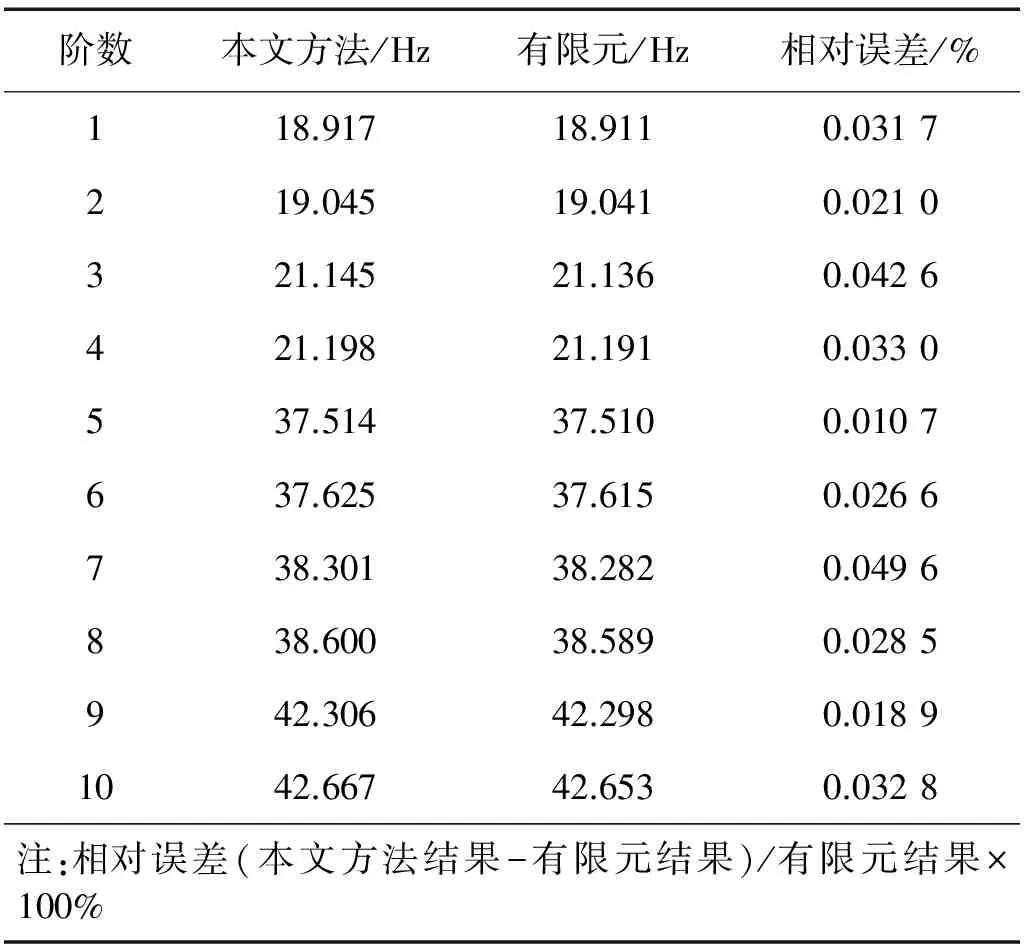
表2 前十阶固有频率对比

图5、图6分别对比了点1、点2的垂向响应，图7给出了系统在固有频率18.9 Hz、37.5 Hz、51.1 Hz、57.7 Hz、73.5 Hz、80.7 Hz时阶梯梁的振型，点1(梁左端)模态位移较小与较大的振型分别如图7(a)和图7(b)所示，本文的计算结果与有限元计算结果重合，验证了本文方法的正确性。

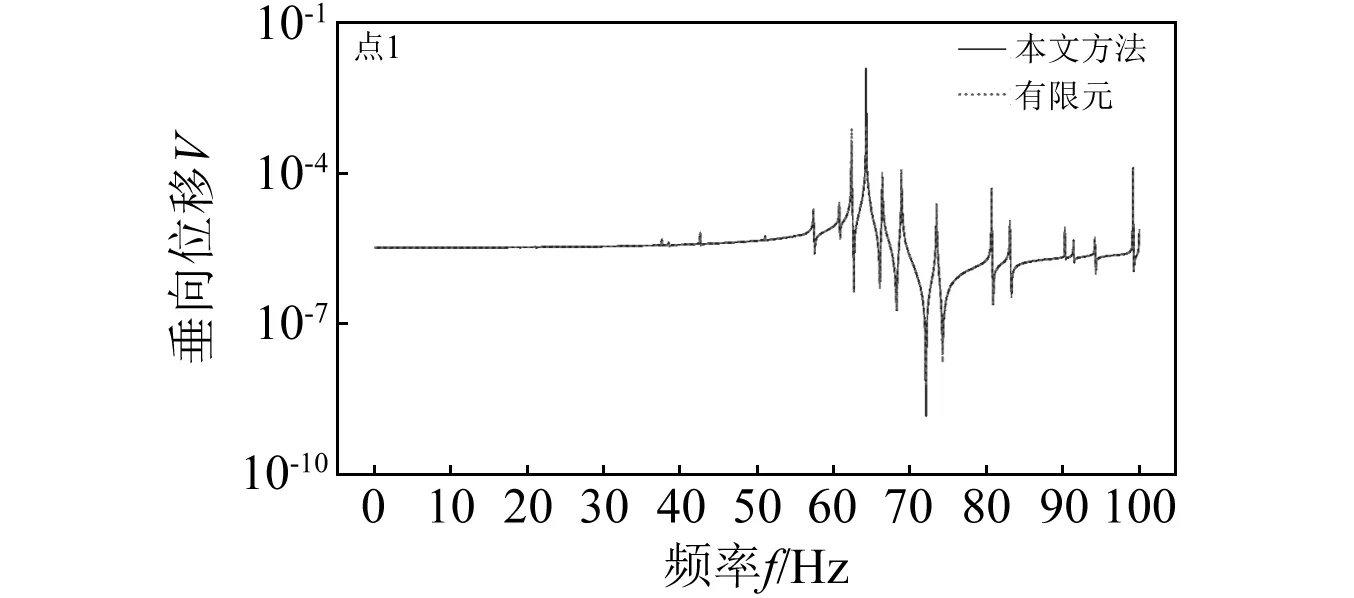
图5 点1处的垂向响应Fig.5 Vertical response of point 1

图6 点2处的垂向响应Fig.6 Vertical response of point 2

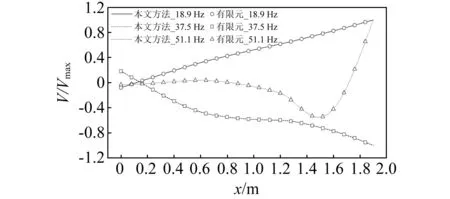
(a)

(b)图7 阶梯梁的六阶垂向振动模态Fig.7 Six vertical vibration modal shapes of the stepped beam

4 偏心对响应的影响

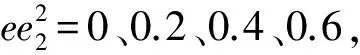
从图8和图9可知，质量偏心对点1处的垂向响应几乎没有影响。但由于纵向响应，质量偏心的存在使梁产生了纵向位移，其响应中的频率特征与垂向响应一致，且其幅值与偏心率成正比。这是因为在建立弯-纵耦合振动方程时，纵向位移以eθ的形式被引入，即产生上述现象。

图8 偏心对点1纵向响应的影响Fig.8 Influence on the longitudinal response of point 1

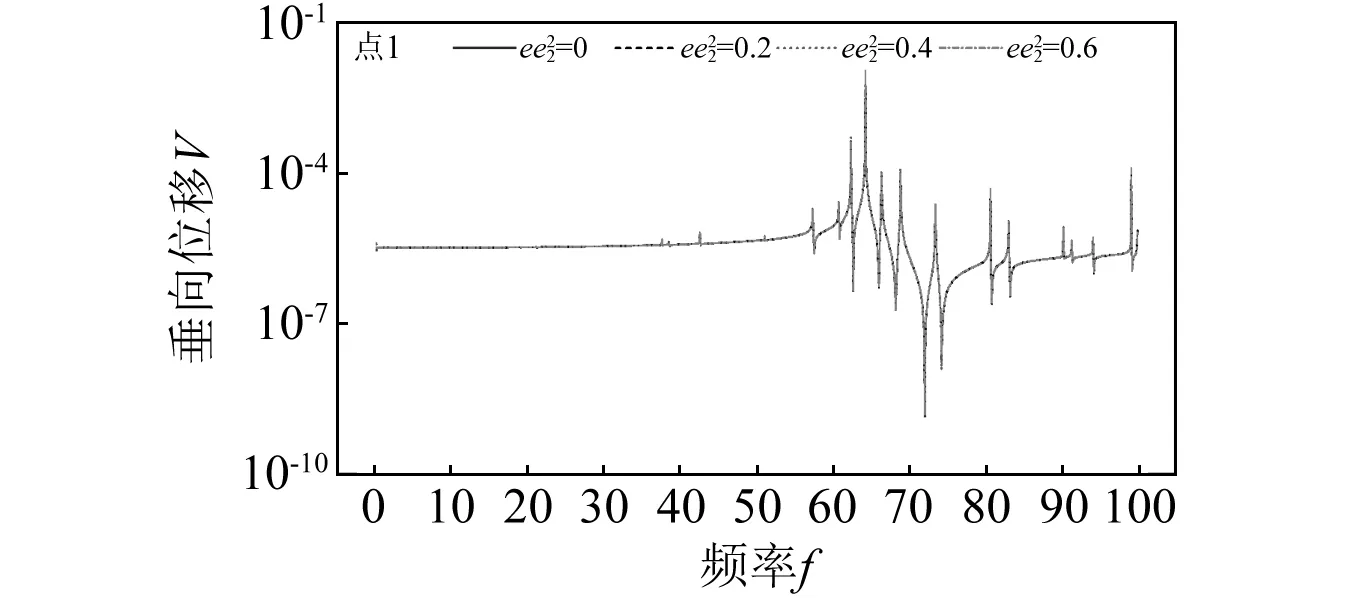
图9 偏心对点1垂向响应的影响Fig.9 Influence on the vertical response of point 1

5 结 论

(1) 本文使用改进的传递矩阵法，结合导纳综合法，给出了求解阶梯梁-基础模型振动问题的步骤。相较于文献[9]所提出的方法，本文的方法可以将相关矩阵的维数控制在6×6，计算效率高，且以矩阵相乘的形式表示子梁端的特性，使得编程较为容易。

(2) 无论是通过解析、数值、还是实验的手段，只要得到与梁连接处基础的导纳矩阵，就可以对系统的振动问题进行求解。通过与有限元计算结果的对比，验证了本方法的正确性。

(3) 纵向位移以eθ的形式被引入梁的弯-纵耦合振动方程，因此，即使单纯在垂向激励下，质量偏心也会引起梁的纵向响应，且其频率特征与垂向响应一致，其幅值与质量偏心程度成正比。质量偏心对梁的垂向响应几乎没有影响。

[ 1 ] LIN H Y. Dynamic analysis of a multi-span uniform beam carrying a number of various concentrated elements[J]. Journal of Sound and Vibration, 2008, 309(1/2): 262-275.

[ 2 ] 崔灿, 蒋晗, 李映辉. 变截面梁横向振动特性半解析法[J]. 振动与冲击, 2012, 31(14): 85-88.

CUI Can, JIANG Han, LI Yinghui. Semi-analytical method for calculating vibration characteristics of variable cross-section beam[J]. Journal of Vibration and Shock, 2012, 31(14): 85-88.

[ 3 ] ZHANG Z, CHEN F, ZHANG Z, et al. Vibration analysis of non-uniform Timoshenko beams coupled with flexible attachments and multiple discontinuities[J]. International Journal of Mechanical Sciences, 2014, 80: 131-143.

[ 4 ] CAO M S, XU W, SU Z, et al. Local coordinate systems-based method to analyze high-order modes of n-step Timoshenko beam[J]. Journal of Vibration and Control, 2017, 23(1): 89-102.

[ 5 ] 王剑, 张振果, 华宏星. 考虑质量偏心 Timoshenko 梁的弯-纵耦合固有振动特性研究[J]. 振动与冲击, 2015, 34(19): 8-12.

WANG Jian, ZHANG Zhenguo, HUA Hongxing. Flexural-longitudinal coupled natural vibration characteristics of a Timoshenko beam considering mass eccentricity[J]. Journal of Vibration and Shock, 2015, 34(19): 8-12.

[ 6 ] JUNGER M C, FEIT D. Sosund, structures, and their interaction[M]. Cambridge: MIT Press, 1986.

[ 7 ] CARESTA M, KESSISSOGLOU N J. Acoustic signature of a submarine hull under harmonic excitation[J]. Applied Acoustics, 2010, 71(1): 17-31.

[ 8 ] HAROLD D N. Rotordynamic modeling and analysis procedures: a review[J]. JSME International Journal Series C Mechanical Systems, Machine Elements and Manufacturing, 1998, 41(1): 1-12.

[ 9 ] BONELLO P, BRENNAN M J. Modelling the dynamic behaviour of a supercritical rotor on a flexible foundation using the mechanical impedance technique[J]. Journal of Sound and Vibration, 2001, 239(3): 445-466.

[10] HONG J, SHAPOSHNIKOV K, ZHANG D, et al. Theoretical modeling for a rotor-bearing-foundation system and its dynamic characteristics analysis[C]//Proceedings of the 9th IFToMM International Conference on Rotor Dynamics. Berlin: Springer International Publishing, 2015: 2199-2214.

[11] WANG Z, LUND J W. Calculations of long rotors with many bearings on a flexible foundation[C]//Third International Conference on Vibration in Rotating Machinery. New York: Conf. Publ., 1984: 11-13.

[12] ZHANG Z, HUANG X, ZHANG Z, et al. On the transverse vibration of Timoshenko double-beam systems coupled with various discontinuities[J]. International Journal of Mechanical Sciences, 2014, 89: 222-241.

[13] RAO S S, YAP F F. Mechanical vibrations[M]. New York: Addison-Wesley, 1995.

[14] COWPER G R. The shear coefficient in Timoshenko’s beam theory[J]. Journal of Applied Mechanics, 1966, 33(2): 335-340.

[15] LEISSA A W. Vibration of shells[M]. New York: Acoustical Society of America, 1993.

Forcedvibrationcalculationofaneccentricsteppedbeam-foundationsystem

WANG Jian1,2， ZHANG Zhenguo1,2， REN Longlong1,2， HUA Hongxing1,2

(1. Institute of Vibration, Shock and Noise, Shanghai Jiao Tong University, Shanghai 200240, China;2. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China)

The vibrations in vertical and longitudinal directions will couple if mass eccentricities are considered in a beam. A theoretical/experimental method focusing on the vibration of an eccentric stepped beam-complicated flexible foundation system was proposed combining the receptance coupling and modified transfer matrix method. The method was validated via the comparison to the results obtained by the FEM. The influence on the response of the system caused by eccentricity was investigated. Eccentricity could hardly affect the vertical response of the system, while it could induce displacement in longitudinal direction even the beam was under vertical excitation. The longitudinal vibration was introduced by the form of eθ, therefore, the associated longitudinal displacement was proportional to eccentricity and its characteristic frequencies were consistent with that of the vertical displacement.

mass eccentricity; stepped beam; flexible foundation; receptance coupling method

国家自然科学基金(51505281)

2016-06-13 修改稿收到日期： 2016-08-12

王剑 男，博士，1988年生

华宏星 男，博士，教授，1955年生

TH113

A

10.13465/j.cnki.jvs.2017.22.019