阻尼材料模量与损耗因子的双边梁测量反演误差机理与控制

屈忠鹏， 盛美萍

(西北工业大学 航海学院，西安 710072)

阻尼材料模量与损耗因子的双边梁测量反演误差机理与控制

屈忠鹏， 盛美萍

(西北工业大学 航海学院，西安 710072)

通过引入中间变量，得到了双边自由阻尼梁阻尼层杨氏模量和损耗因子的简化反演公式，并在此基础上进行误差分析，给出了高阶误差预测公式。研究表明，影响反演精度的重要参数为复合梁与基底梁的刚度比；刚度比越大，反演精度越高；当刚度比接近于1时，共振频率比和质量比的误差放大倍数急剧增加，导致反演误差变大；通过增大阻尼层与基底层的厚度比和模量比，可以增大刚度比，进而提高反演精度。仿真分析验证了该结论的正确性。

阻尼材料； 弯曲共振法； 双边梁； 误差分析； 刚度比

阻尼技术可以在较宽频带内对振动噪声进行有效控制，是减振降噪的一个重要手段，因此阻尼材料广泛应用于船艇、飞行器、汽车和建筑降噪等诸多领域[1-2]。阻尼材料的重要特性参数为模量和损耗因子，其获取主要依赖于试验测量[3-5]。

弯曲共振法是阻尼测量的常用方法之一，具有试验架构简单、测量频带宽等优点。但是，因为需要根据基底梁与复合梁的特性差别对模量和损耗因子进行反演[6-7]，所以其计算结果对测量误差较为敏感。为有效控制误差和指导试件设计，工程人员需清楚了解误差传递的特征。通过引入误差放大因子的概念，朱蓓丽等[8-9]对夹心梁结构、胡卫强等[10-11]对单边和双边自由阻尼梁结构分别进行了研究，得到试件设计的若干指导意见。但由于反演公式复杂，作者们借助符号运算进行分析，或仅进行了部分推导，无法得到误差放大因子的解析表达式，因此难以清晰揭示误差传递的本质。

本文针对双边自由阻尼梁结构开展研究。通过引入中间变量，对复杂的反演公式进行了化简，从而避免了符号运算，得到误差放大因子的解析表达式，并进一步给出了更准确的高阶误差预测公式。在此基础上，提出改善测量精度的途径，并通过仿真分析进行了验证。

1 理论基础

对于双边自由阻尼复合梁(见图1)，阻尼层杨氏模量和损耗因子反演公式为

(1)

(2)

式中：E1为基底层杨氏模量；ηc为复合梁损耗因子；F为复合梁与基底梁的共振频率比；D和T分别为阻尼层与基底层的密度比和厚度比。实际测量中，D通过复合梁和基底梁的质量比S获得，其关系为

D=(S-1)/(2T)

(3)

复合梁与基底梁的刚度比为

ε=F2S

(4)

并记厚度比参量

τ=8T3+12T2+6T

(5)

将式(3)～式(5)代入式(1)和式(2)，整理可得

(6)

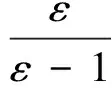
(7)

整理后公式形式简洁，便于进行误差分析。

图1 双边自由阻尼梁Fig.1 The symmetric free-layer beam

2 误差分析

根据误差放大因子定义，阻尼层杨氏模量和损耗因子的误差可表示为

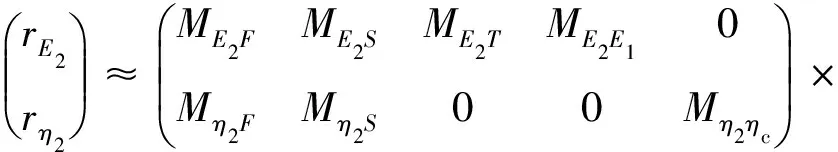
(8)

(9)

(10)

式(9)和式(10)分别为与杨氏模量E2和损耗因子η2相关的误差放大因子。其中ME2E1和Mη2ηc的值为1， 这表示E1和ηc的误差会等量传递给E2和η2。ME2T的值与厚度比T有关， 介于-3～-1，这表示T的误差会被放大1～3倍，但方向相反。ME2F、ME2S、Mη2F和Mη2S的值仅由刚度比ε决定， 并且F的误差放大倍数为S的2倍。将式(6)变形可得刚度比为

ε=(8T3+12T2+6T)e+1

(11)

式中：e=E2/E1为阻尼层与基底层的模量比。 一般而言，e≪1， 可见刚度比ε略大于1。

各误差放大因子随ε变化的曲线，如图2所示。 当刚度比较小时，F与S的误差放大因子明显高于其它值， 这使得F和S的误差被放大数十倍甚至上百倍，将会导致阻尼层杨氏模量和损耗因子的反演精度急剧降低。随着刚度比ε增大，F与S的误差放大因子减小， 当εgt;1.2时， 其值降至与其它放大因子相同的量级。

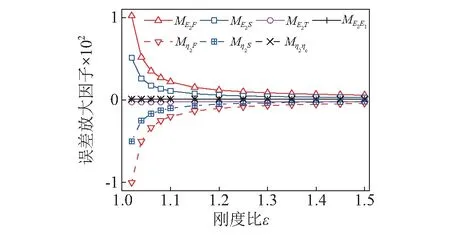
图2 误差放大因子比较Fig.2 Comparison of the error magnification factors

由上述分析可知，提高刚度比ε可有效控制反演误差。 由式(11)可见提高ε有两个途径： 增加厚度比T和模量比e。厚度比T可通过增加阻尼层厚度或减小基底层厚度而增加，模量比可通过更换较软基底层而增加。而当ε较小时， 频率比F和质量比S的误差应受到严格控制。

误差放大因子根据一阶泰勒展开获得，用于分析误差传递特性是足够的。若是要更精确地预测误差，则需进行高阶计算。对式(6)和式(7)进行完整泰勒展开可得

(12)

其中rε和rτ为中间变量的相对误差，可通过式(4)和式(5)求得

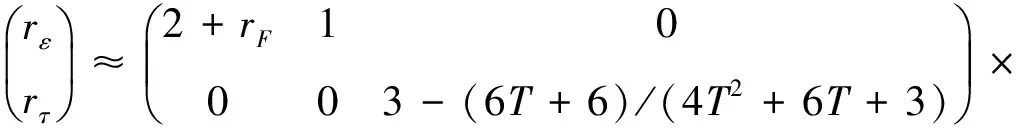
(13)

3 仿真验证

阻尼材料的特性参数一般随频率有所变化。这里将杨氏模量和损耗因子均设为常值，这不影响结果的验证，但可简化分析和讨论过程。假定某阻尼材料的杨氏模量为100 MPa，损耗因子为0.4，其厚度为1 mm。选择三个试件进行分析，试件1选用钢材料为基底层，厚度为1 mm；试件2减小基底层的厚度为0.5 mm；试件3将基底选为有机玻璃，厚度为1 mm。试件长度均为200 mm。阻尼材料、钢和有机玻璃的密度分别为1 200 kg/m3、7 800 kg/m3和1 200 kg/m3，钢和有机玻璃的模量分别为200 GPa和5 GPa。三个试件复合梁与基底梁的刚度比由小变大，依次为1.01、1.06和1.52。

仿真得到的频响曲线，如图3所示。从其中可识别得到共振频率比F和复合梁的损耗因子ηc。将频率比F、质量比S、厚度比T、 基底模量E1和复合梁损耗因子ηc的随机误差均取为0.5%， 使用式(1)和式(2)反演阻尼层的杨氏模量和损耗因子。

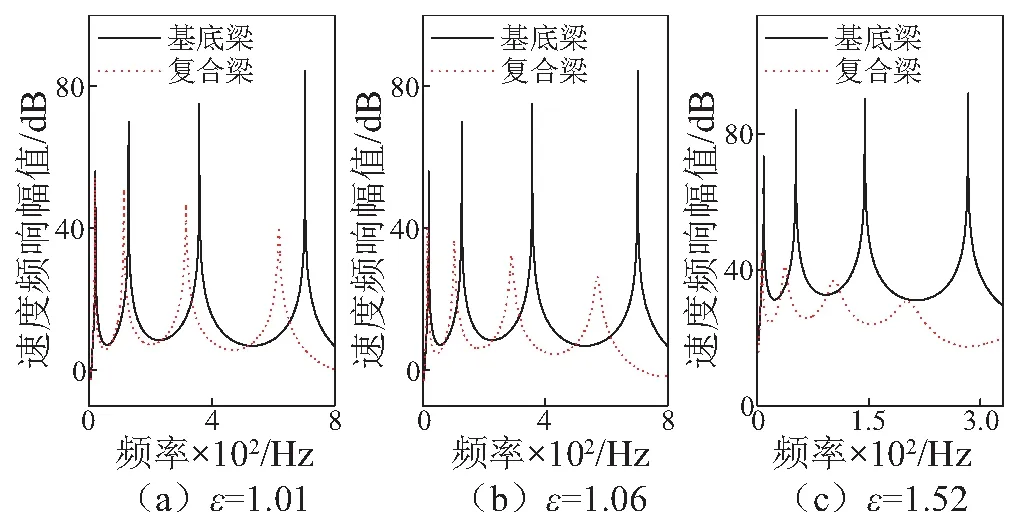
图3 三个试件仿真频响曲线Fig.3 Simulated velocity frequency response of the three specimens

图4为三个试件反演结果的对比。可见随着刚度比增大，杨氏模量和损耗因子的反演误差均减小。表1为误差的具体值，其中实际值由图4数据计算得到，一阶和高阶估计分别是式(8)和式(12)的预测结果。由表1可知，杨氏模量的误差预测值与实际值接近，且一阶与高阶估计差别很小。对于损耗因子，当ε较小时，一阶估计的误差预测值偏大，随着ε变大，一阶和高阶估计的结果趋向实际值。整体而言，随着刚度比增大，反演精度明显提高。

进一步分析可知，试件1反演误差大的主要原因是刚度比ε接近于1，导致F、S的误差急剧放大。针对试件1，将频率比F、质量比S的随机误差减至0.1%，同时保持厚度比T、基底模量E1和复合梁损耗因子ηc的随机误差不变，进行反演。

图4 三个试件反演结果对比Fig.4 Comparison of the calculating results of the three specimens

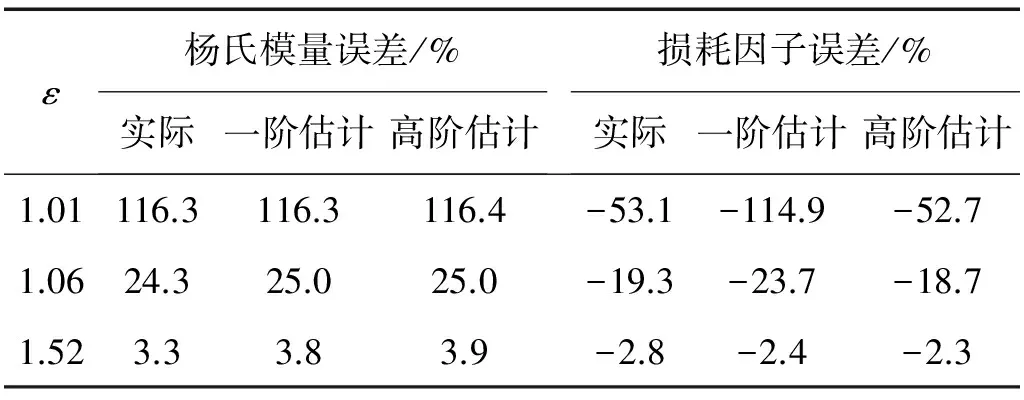
表1 三个试件反演误差

图5为频率比F、质量比S误差减小前后，杨氏模量和损耗因子反演结果的对比。可见F、S误差减小后，反演误差明显变小。表2为误差的具体值，其中总误差由图5数据计算，F、S的误差放大量根据式(12)计算。对比总误差与F、S的误差放大量可知，总误差几乎全部由F、S的误差引起。因此，当ε较小时，为保证阻尼层杨氏模量和损耗因子的反演精度，应严格控制试件共振频率和质量的测量误差。

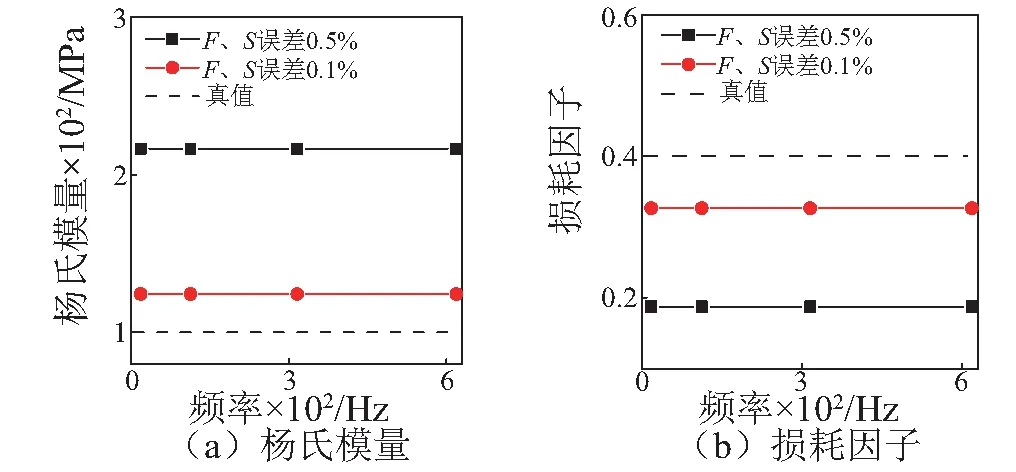
图5 频率比F、质量比S误差对反演结果影响Fig.5 Effects of the errors of F and S on the calculating results

表2 频率比F、质量比S误差对反演精度影响

4 试验验证

为进一步验证分析的结果，使用两组刚度比不同的试件测量了聚氨酯橡胶材料的特性。两组试件的基底层均为不锈钢，其厚度分别为1 mm和0.5 mm，聚氨酯橡胶的厚度均为2 mm，因厚度比不同，两组试件刚度比ε产生差异，分别约为1.03和1.13。第一组试件基底层和阻尼层质量分别为8.2 g和10.1 g，第二组分别为16.4 g和10.3 g。试件长度和宽度分别为225 mm和10 mm。测量的频率间隔为0.25 Hz，质量测量精确到0.1 g。

图6为测得的频响曲线。从图中识别出共振频率比F和复合梁的损耗因子ηc，然后反演阻尼层的杨氏模量和损耗因子。

图6 两组试件频响曲线Fig.6 Experimental velocity frequency response of the two specimens

图7为杨氏模量和损耗因子的反演结果，图中实心标记为实测数据的反演结果。两组结果存在一定差异，这是由第一组刚度比ε较小引起的，因为小的刚度比会导致测量误差急剧放大，例如，计算可得第一组质量比S的误差放大倍数约为33倍，而第二组仅为8倍。为对此进行验证，假定阻尼层质量存在0.1 g的测量误差，重新反演可得到空心标记的结果。可见对于第一组，杨氏模量和损耗因子的结果均有较大偏移，而第二组的偏移量明显更小。这证明了相同测量误差条件下，当刚度比值较大时，有利于提高测量的稳定性，从而提高精度。同时也证明了质量比S是引起反演误差的一个主要因素，类似地也可验证频率比F的影响。

图7 两组试件反演结果对比Fig.7 Comparison of the calculating results of the two specimens

5 结 论

得到了双边自由阻尼梁阻尼层杨氏模量和损耗因子的简化反演公式，并在此基础上进行误差分析，给出了高阶误差预测公式。研究表明：

(1) 复合梁与基底梁的刚度比ε是影响误差放大的重要因素。相同测量误差条件下，ε越大，杨氏模量和损耗因子反演精度越高。

(2) 通过增大厚度比T和模量比e可以增大刚度比ε，从而提高反演精度。

(3) 当刚度比ε较小时，频率比F与质量比S的误差是引起反演误差的主要因素。

(4) 使用高阶误差预测公式，可以对杨氏模量和损耗因子的误差进行准确预测。

[ 1 ] JONES, DAVID I G. Handbook of viscoelastic vibration damping[M]. [S.l.]: Wiley, 2001: 259-262.

[ 2 ] 黄志诚，秦朝烨，褚福磊. 附加黏弹阻尼层的薄壁构件振动问题研究综述[J]. 振动与冲击, 2014, 33(7): 105-113.

HUANG Zhicheng, QIN Zhaoye, CHU Fulei. A review about vibration problems of thin-walled structures with viscoelastic damping layer[J]. Journal of Vibration and Shock, 2014, 33(7): 105-113.

[ 3 ] RENAULT A, JAOUEN L, SGARD F. Characterization of elastic parameters of acoustical porous materials from beam bending vibrations[J]. Journal of Sound and Vibration, 2011, 330(9): 1950-1961.

[ 4 ] 尹邦辉，王敏庆，吴晓东. 结构振动阻尼测试的衰减法研究[J]. 振动与冲击, 2014, 33(4): 100-106.

YIN Banghui, WANG Minqing , WU Xiaodong. Decay method for measuring structural vibration damping[J]. Journal of Vibration and Shock, 2014, 33(4): 100-106.

[ 5 ] PEREIRA R, ARENAS J P, ZUMELZU E. Comparison of four test methods to measure damping properties of materials by using piezoelectric transducers[J]. Materials amp; Design, 2011, 32(4): 2423-2428.

[ 6 ] Standard test method for measuring vibration damping properties of materials: ASTM E756-05 [S]. [S.l.]: American Society for Testing and Materials, 2010.

[ 7 ] 声学材料阻尼性能的弯曲共振测试方法: GB/T 16406—1996 [S]. 北京：国家技术监督局,1996.

[ 8 ] 朱蓓丽, 沈庆元. 黏弹性材料复剪切模量的测量及误差分析[J]. 噪声与振动控制, 1999(6): 38-41.

ZHU Beili, SHEN Qingyuan. Measurement of the viscoelastic material’s complex shear modulus and the error analysis[J]. Journal of Noise and Vibration Control, 1999(6): 38-41.

[ 9 ] 马少璞, 王敏庆, 胡卫强，等. 对称夹层结构的共振梁法理论误差研究[J]. 噪声与振动控制, 2008,28(4): 38-41.

MA Shaopu,WANG Minqing, HU Weiqiang, et al. Study on theoretical error of the resonance beam testing method about sandwich specimen[J]. Journal of Noise and Vibration Control, 2008,28(4): 38-41.

[10] 胡卫强, 王敏庆, 刘志宏. 悬臂梁弯曲共振法自由阻尼结构试件设计研究[J]. 实验力学, 2008, 23(3): 241-247.

HU Weiqiang, WANG Minqing, LIU Zhihong. Study of the design of free-damping form specimen in resonance method[J]. Journal of Experimental Mechanics,2008,23(3): 241-247.

[11] 王超, 吕振华. 黏弹性阻尼材料力学参数测试实验用双边附加自由结构阻尼试件设计方法研究[J]. 振动与冲击, 2014, 33(5): 102-108.

WANG Chao, LÜ Zhenhua. Research on the design of specimens damped both sides used in the measurement of viscoelastic material’s mechanical parameters[J]. Journal of Vibration and Shock, 2014, 33(5): 101-108.

Erroranalysisofthesymmetricfree-layerbeammethodfordeterminingYoung’smodulusandlossfactorofdampingmaterials

QU Zhongpeng, SHENG Meiping

(School of Marine Science and Technology, Northwestern Polytechanical University, Xi’an 710072, China)

The inverse formulas of the symmetric free-layer beam method were simplified by introducing the medium variables. Based on the simplified formulas, a total error analysis was made and the higher order expressions for error prediction were derived. The research shows that the stiffness ratio is the most significant factor influencing the inverse accuracy. More accurate results can be obtained from specimens with bigger stiffness ratios. The errors of the frequency ratio and the mass ratio are violently magnified as the stiffness ratio reaches 1, which will lead to great inverse errors. The stiffness ratio can be increased by increasing the thickness ratio and the modulus ratio between the damping and the base layer. Thus the inverse accuracy will be improved. The conclusion was verified by simulation analysis.

damping materials; flexural resonance method; symmetric free-layer beam; error analysis; stiffness ratio

2016-05-30 修改稿收到日期： 2016-09-07

屈忠鹏 男，博士生，1989年生

盛美萍 女，博士，教授，1970年生

TB535.1

A

10.13465/j.cnki.jvs.2017.22.016