被动雷达导引头宽带信号时差测角方法研究

潘金波， 狄 慧， 宗 剑， 胡天俊

(1.上海机电工程研究所， 上海 201109； 2.上海卫星工程研究所， 上海 201109； 3.上海无线电设备研究所， 上海 200090)

被动雷达导引头宽带信号时差测角方法研究

潘金波1， 狄 慧2， 宗 剑3， 胡天俊1

(1.上海机电工程研究所， 上海 201109； 2.上海卫星工程研究所， 上海 201109； 3.上海无线电设备研究所， 上海 200090)

随着雷达系统的综合化，信号带宽越来越宽是雷达信号辐射源的发展趋势。宽带信号时宽带宽积大，具有时差估计精度高的优势。利用该优势，研究了基于时差估计的无源导引头测角方法。利用傅里叶变换将宽带信号时差估计转换为频率估计获得较高的精度。通过理论推导出来该方法的时差估计精度表达式，进一步得出测角精度表达式。针对不同信号带宽做了时差估计精度仿真，以及不同时差精度、不同入射角情况下的测角精度仿真。仿真结果表明，该方法相对于干涉仪测角方法，不需要解相位模糊并且能够显著提高宽带信号测角精度。

被动雷达导引头； 测角精度； 时差估计； 离散傅里叶变换

0 引言

随着微电子技术的发展，采用宽带、多功能的综合电子系统取代功能单一的雷达成为一种趋势。在下一代先进辐射源中，超宽带多频段的使用将是实现多功能的基本要求[1-2]。本文针对宽带辐射源信号，研究了基于时差精确估计的被动导引头测角方法。

被动导引头常用的测角方法为干涉仪鉴相方法[3-5]，为了获得较高的测角精度，干涉仪的基线通常大于半波长，存在相位模糊问题，解相位模糊需要采用多通道接收以及相应的处理算法。针对宽带信号，由于信号能量在频谱上分散，鉴相误差增大，在弹上资源有限的情况下难以获得较高的测角精度。文中利用宽带辐射源信号时差估计精度较高的特点，通过精确估计不同接收通道信号的到达时差来提高被动雷达导引头的测角精度。与干涉仪鉴相方法相比，时差测角所需的天线阵列以及接收通道数较少，相较于干涉仪法需要解模糊，处理算法简单。由于弹体尺寸的限制，不同天线之间的时差值较小，远小于脉冲宽度，不会出现时差模糊的脉冲配对问题，时差测角精度主要由时差估计精度来保证。

1 测角方法基本原理

在满足远场条件的情况下，信号源来波信号通常可以看作是平行波入射，如图1所示，其中θ为来波信号入射角。

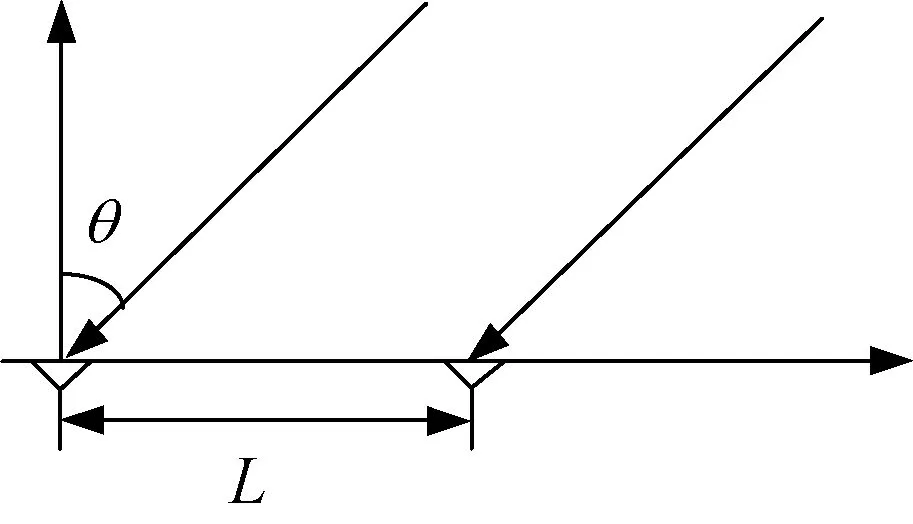
图1 测向原理示意图

常用的测角方法有比幅测角法和相位干涉仪测角法，比幅测角法原理简单，但测向精度与天线的波束宽度相关，测角精度相对较低。相位干涉仪测向法则因其测角精度较高，应用广泛。

采用干涉仪测角法时，不同接收天线接收到的辐射源来波信号相位差与入射角度之间满足如下关系：

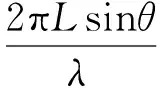
(1)

式中：φ为天线相位差；L为基线长度；λ为来波信号波长。

且可得测角精度表达式为

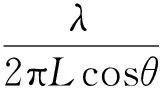
(2)

从式(1)可以估计出相位差,即可得到辐射源信号入射角度。由于相位差的特殊性质，当天线之间的距离大于半波长时，会出现2π的模糊。从测角精度表达式可以得到，测角精度和天线间距成反比，为了避免相位模糊而缩短天线间距，会降低测角的精度。当天线间距大于半波长时，则需要设计相应的相位解模糊方法，使用较多的有长短基线解模糊法、参差基线解模糊法，这些方法都需要增加接收天线及通道，并且需要相应的解模糊算法，增加了后端处理的难度，在弹体资源有限的情况下，难以达到满意的测角精度。并且当辐射源信号为宽带信号时，信号在频谱上分布较分散，会降低干涉仪的鉴相精度，最终影响测角精度。

辐射源入射信号至不同接收天线的相位差本质上是到达天线的时刻不同造成的，可以从时差与入射角度的关系入手，通过获得较高精度的时差估计值来获得角度估计值。时差Δt和入射角的关系如下式：

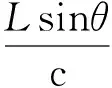
(3)

式中：c为光速。式(1)中相位差估计值和信号波长相关，即需要具备信号频率的先验知识，或者精确估计出频率，但仍然会引入误差项，和式(1)相比，式(3)的入射角仅和到达时间差的估计误差有关系，误差量较少。根据时差估计的精度分析，信号带宽越大，时差估计越精确，基于时差估计的测角方法相较于基于相位差的测角方法更适用于宽带信号。

基于时差的被动导引头采用天线与弹体截面共形设计。天线采用共形4元圆形天线阵列，如图2所示，在弹体坐标系下，1/3天线完成方位角测算，2/4天线完成俯仰角测算。

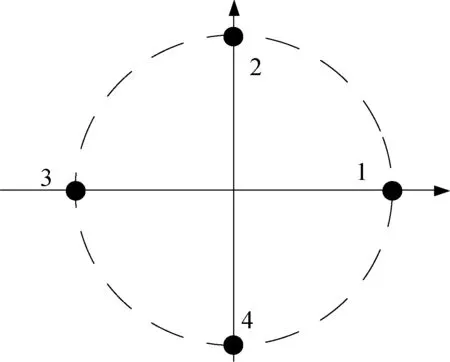
图2 天线弹体截面布局图

基于时差的被动导引头信号接收及处理系统如图3所示。系统由三部分组成：4阵元均匀的共形天线阵列、射频前端及变频部分、4通道接收机，信号接收机处理部分完成信号分选与识别、时差及角度运算功能。

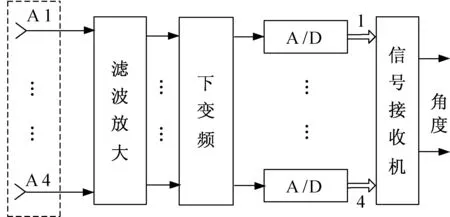
图3 基于时差的被动导引头组成框图

2 宽带信号时差精估计原理

时差估计方法常用的有到达时间作差值法以及直接相关求时差两种方法。由于弹体的尺寸限制，天线之间的间距有限，以直径30 cm为例，辐射源信号到达两个天线的最大时差为1 ns，可见时差间距是小于一个采样间隔的，在数字接收机中，难以通过测量每个信号的到达时间来获得时差估计值。那么，考虑采用相关的方法直接估计宽带信号的时差值。

两接收天线接收到的信号表达式分别为

(4)

式中：s1(t)、s2(t)为信号，s2(t)是在s1(t)信号基础上叠加一个时差τ;w1(t)、w2(t)为噪声。经滤波放大、变频以及数字采样后，两天线接收信号的离散形式分别为

(5)

式中:ts为采样间隔；D是量化时差，D=τ/ts。对采样后的数字信号x1(n)、x2(n)作离散傅里叶变换(DFT)，可得

(6)

式中：S1(k)、W1(k)、W2(k)是离散信号s1(n)、w1(n)、w2(n)的DFT变换。将X1(k)和X2(k)共轭相乘得

(7)

式中：W(k)为等效噪声；|S1(k)|2是接收信号s1(n)频谱模的平方。对于常见的宽带信号调制样式，信号的频谱抖动不大，即|S1(k)|2变化频率不会太高，因此可以将R(k)看作幅度调制为|S1(k)|2，载波频率为D，采样速率为N的“正弦波信号”，信号的等效“脉冲宽度”为原信号s1(t)的带宽B。

通过将不同通道的信号经DFT变换和共轭相乘处理后，可将信号时差的估计转化为构造出的正弦波信号频率的估计。信号频率估计的精度与信号的有效脉冲宽度有关，构造出的正弦波脉宽越大频率估计精度越高;而构造信号的脉宽和原信号的带宽相关，也即原信号的带宽越宽，时差估计精度越高。由于幅度的稳定度受信号的不同调制样式影响，一定程度上会影响到时差估计精度。构造出的信号能量集中在信号带宽内，采用带宽内除信号带宽其余频带部分为噪声，会降低频率估计精度。利用门限值比较法估计出构造信号的脉冲宽度，将脉冲宽度区间外的其余数据置零后再估计频率，可以获得部分信噪比增益，进而提高频率估计精度。

对经过上述处理的R(k)作DFT运算，搜索最大谱线位置，设为l。由于频率分裂的原因，第一步搜索出的频率值精度达不到测角精度要求。为提高频率估计精度，选取区间[l-0.5,l+0.5]进一步作DFT运算：

(8)

式中：N为构造信号的离散点数；m=l-0.5,L1-0.5+1/i,…,l+0.5；i是DFT算法的插值率，选取大于1的正整数。i的取值直接影响频率估计精度和运算量。综合精度要求和弹上有限的资源，并经过仿真运算，i取值为32，计算量满足弹上资源限制并且能保证时差估计精度。区间搜索的谱线峰值位置设为P，|F(m)|在峰值P附近的值可以用抛物线近似表示，则时差D的精估计值表达式为[6-7]

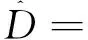
(9)

3 时差估计测角精度分析

对式(3)左右两边作微分，可得

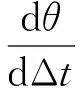
(10)

从式中可以得出，测角精度和时差测量精度成正比，和入射角的余弦以及天线间距成反比。首先分析本文宽带信号时差估计方法的精度。

本文方法估计辐射源信号到达两个天线的时差时，通过作DFT变换，将时差估计转化为频率估计，即实际采用的是频率估计算法。由于频率估计采用是差值DFT算，是最大似然的，因此频率估计的方差误差近似于正弦波信号频率估计的克拉美-罗限[8]：

(11)

式中：T为信号脉冲宽度；N为信号脉宽内的采样点数；S为信噪比。

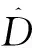
信号构造的过程中通过识别信号的有效部分提高了信噪比，式(7)中等效噪声的均值为0，方差推导如式(13)所示。

D[W(k)] = E[|W(k)|2]

=E[|S1(k)|2|W1(k)|2]+

E[|S1(k)|2|W2(k)|2]+

E[|W1(k)|2|W2(k)|2]

=2E[|S1(k)|2]σW2+σW4

(13)

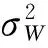
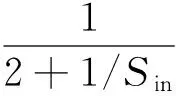
(14)

式(14)中在输入信噪比大于1 dB条件下可作上述近似。提取信号有效带宽时信号能量无损失，而噪声能量只保留了有效带宽内的部分，即变为原信号的B/fs倍，则有

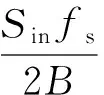
(15)

将式(15)代入式(11)时差估计的方差表达式：

(16)

将式(16)代入式(10)可以得到测角的方差表达式为

(17)

4 仿真实验及结果分析

从上述测角精度的分析可以得出，测角精度和时差估计精度成正比，与入射角的余弦以及天线基线长度成反比。针对这三个因素，通过两个仿真实例分析时差测角的精度。

首先分析不同带宽的信号在不同输入信噪比条件下的时差估计精度。仿真实例一参数设置为：入射角30°，天线基线长度30 cm；采样频率1 GHz，信号频率356.43 MHz，调频方式为线性调频，信号脉冲宽度10 μs信号带宽分别设置为10，20，50 MHz，输入信噪比设置为0～30 dB，每个试验条件下500次门特卡罗试验。不同带宽信号时差估计均方根误差随输入信噪比变化如图4所示，从图中可以得出随着信号带宽的增大，时差估计精度随之增加，在输入信噪比大于15 dB时，时差估计精度优于0.1 ns。

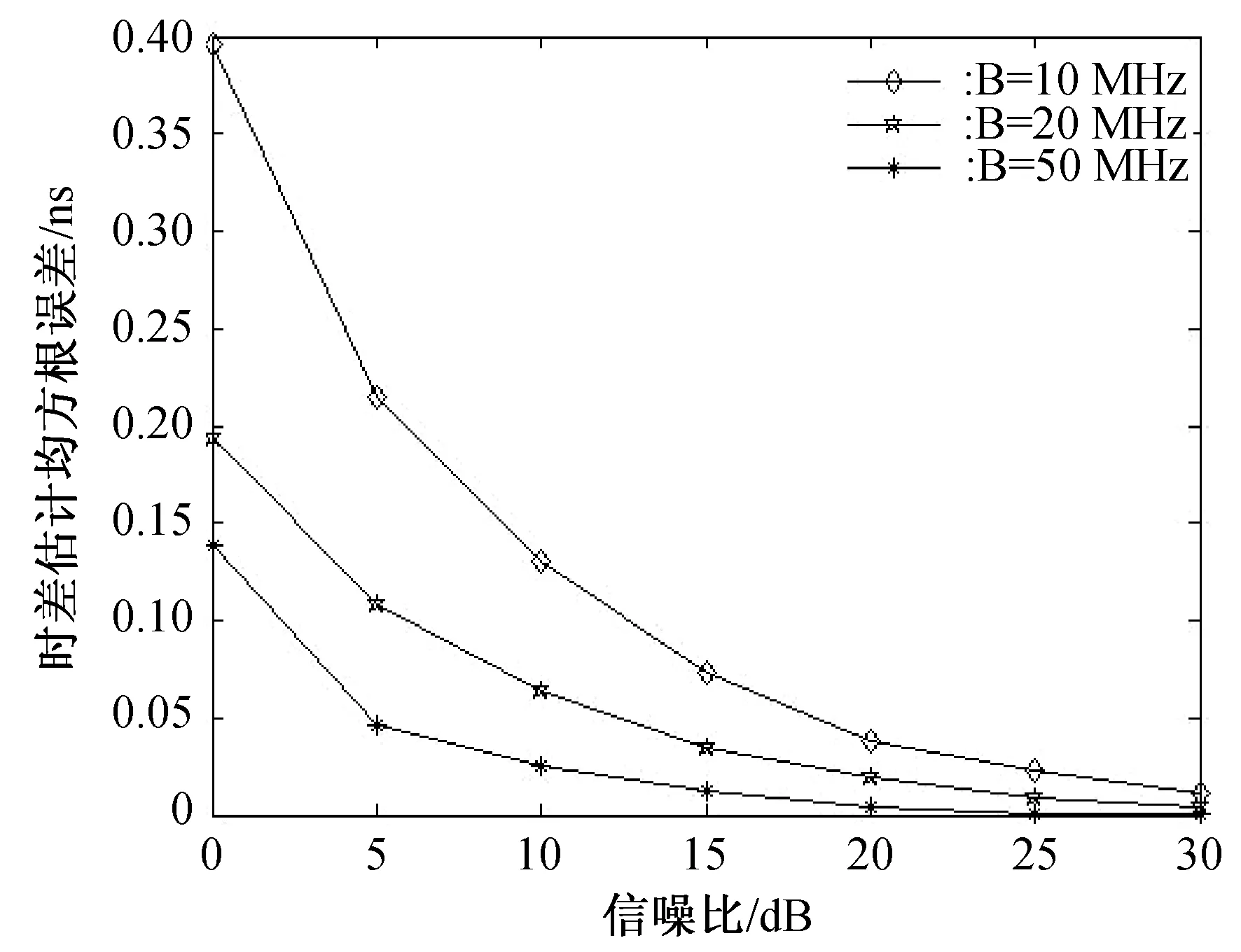
图4 不同带宽信号时差估计精度随输入信噪比变化比较

接下来分析不同入射角情况下，时差估计均值与真实值之间的偏差以及根据时差运算出的角度与入射角之间的关系。仿真实例二参数设置为：天线基线长度30 cm；采样频率1 GHz，信号频率356.43 MHz，调频方式为线性调频，带宽为20 MHz，信号脉冲宽度10 μs，随着入射角由1°～80°设置，每个仿真条件做500次门特卡罗试验。不同输入信噪比条件下，时差估计均值以及角度估计均值与真实值比较分别如图5和图6所示。

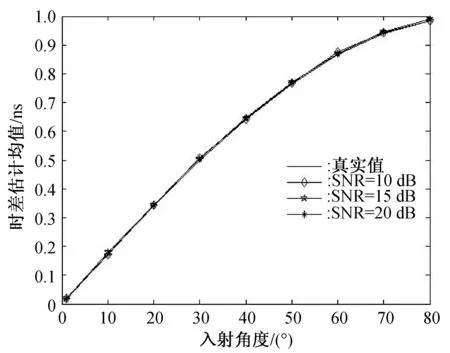
图5 不同信噪比信号时差估计均值随入射角变化比较

图6 不同信噪比信号角度估计均值随入射角变化比较

从图5中可以看出，在不同的入射角情况下，时差估计均值均趋近于时差真值，图6中显示角度估计均值在大入射角情况下略偏离真值。

不同输入信噪比条件下，时差估计以及角度估计均方根误差分别如图7和图8所示。

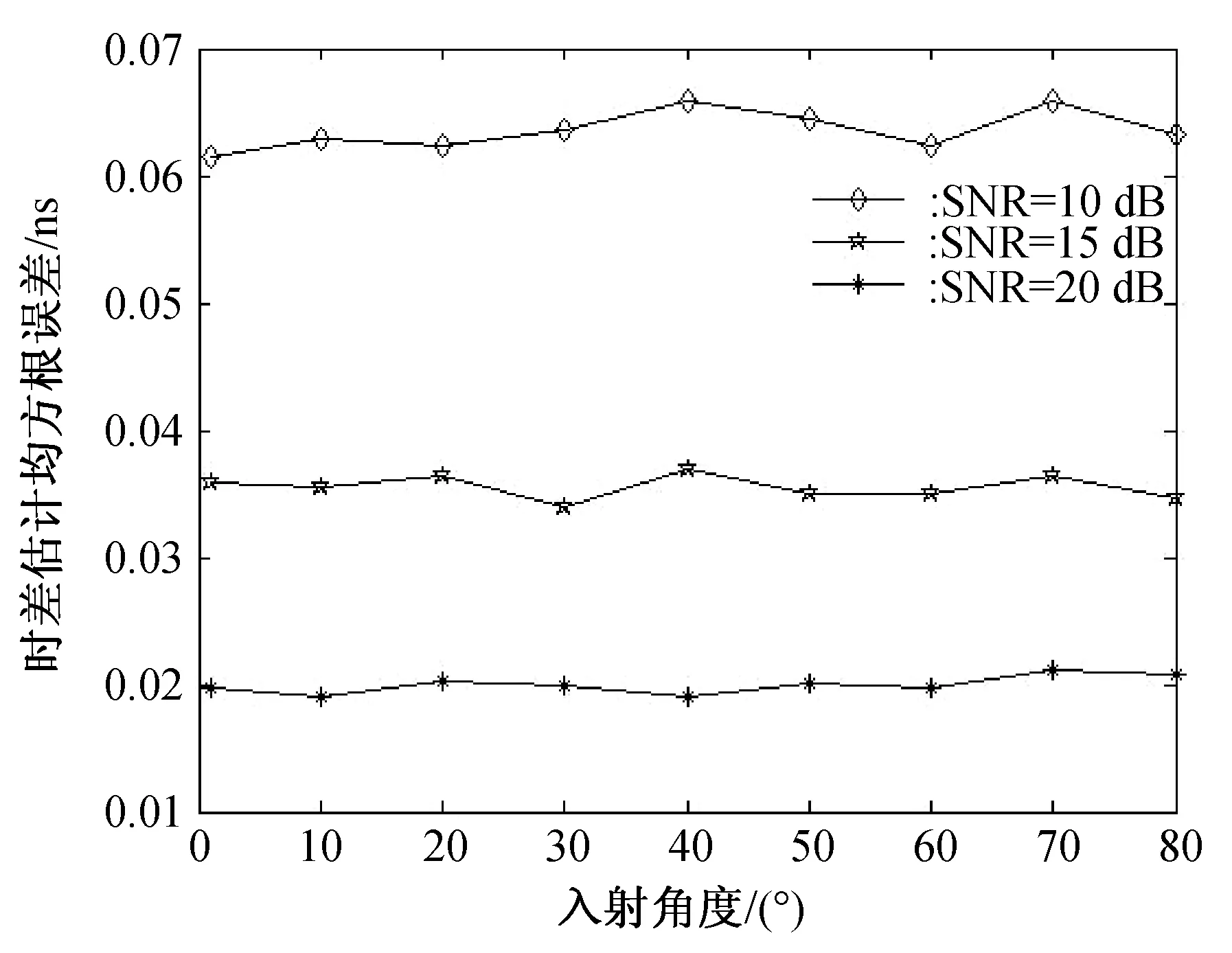
图7 不同信噪比时差估计精度随入射角度变化比较

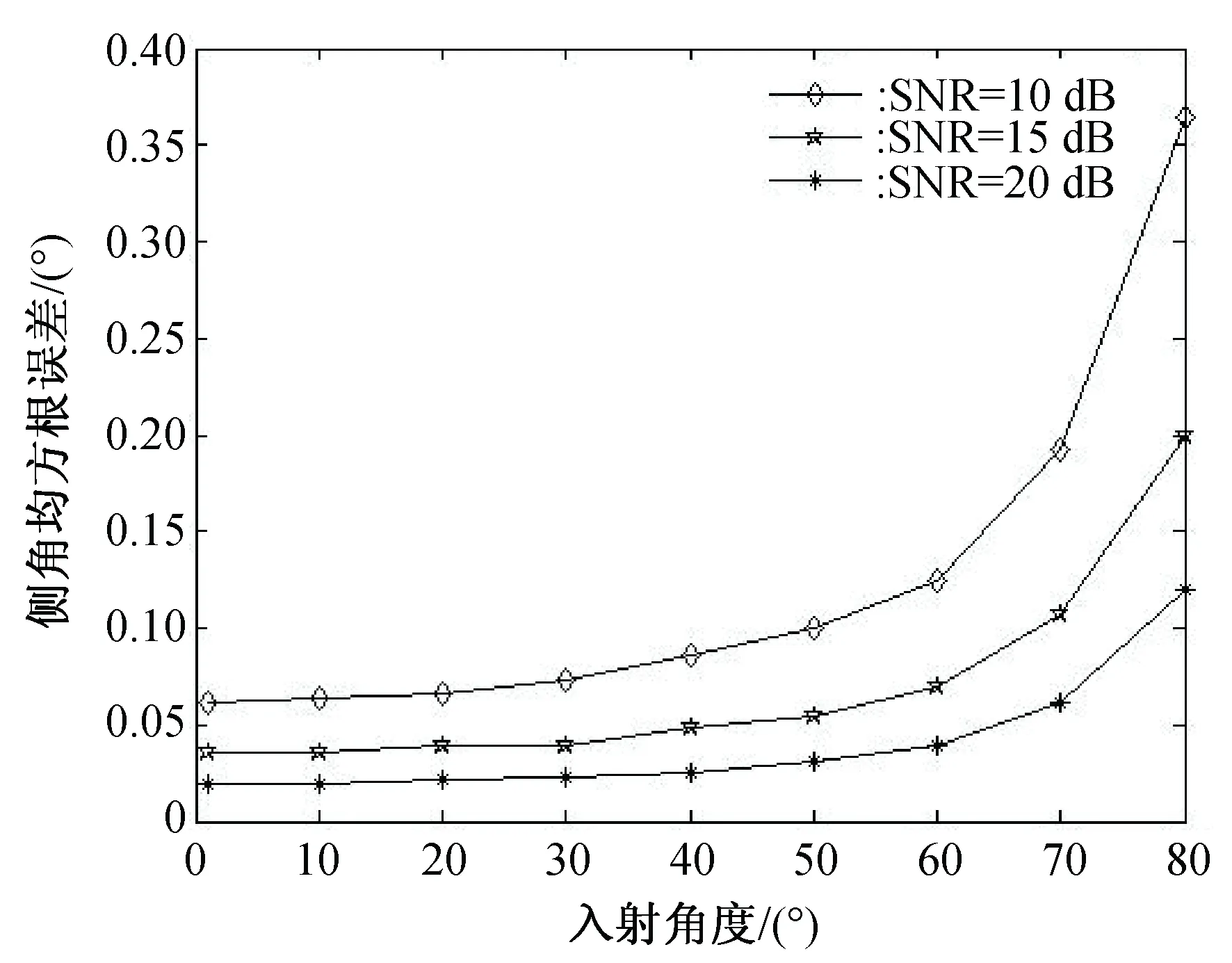
图8 不同信噪比角度估计精度随入射角度变化比较

从图中可以看出，在不同的入射角情况下，时差估计误差随着信噪比的增大趋于稳定，不受入射角度变化影响。角度估计误差在40°以内能达到0.1°以下，信噪比条件好的情况下能小于0.05°，在大入射角情况下测角精度变差，约为0.4°。

5 结论

本文分析了一种针对宽带信号的无源导引头测角方法，利用宽带时差估计精度高的优势提高宽带信号测角精度。分析给出了基于离散傅里叶变换的宽带信号时差精确测量方法，从理论推导和仿真验证两方面研究了宽带信号时差估计的影响因素以及测角精度的影响因素。仿真结果表明，在入射角小于40°的情况下，测角精度能到0.05°，大幅提高了测角精度。

[1] 陈国海.下一代预警机雷达技术[J]. 现代雷达， 2010， 32(3)： 1-4.

[2] 杨建宇.雷达技术发展规律和宏观趋势分析[J]. 雷达学报， 2012， 1(1)： 19-27.

[3] 宋才水，盛晓文，顾尔顺. 捷联干涉仪体制被动导引头测角解模糊算法[J]. 现代防御技术， 2004， 32(4)： 48-53.

[4] 曲志昱，司锡才. 基于虚拟基线的宽带被动导引头测向方法[J]. 弹箭与制导学报， 2007， 27(4)： 92-95.

[5] 张亮，徐振海，熊子源，等. 基于圆阵干涉仪的被动导引头宽带测向方法[J]. 系统工程与电子技术， 2012， 34(3)： 462-466.

[6] Bai Y C, Zhang X G, Tang L. Subsample Time Delay Estimation Based on Phase Spectrum of Band Limited Stochastic Signals[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2010, 27(2): 170-175.

[7] Jacovitti G, Scarano G. Discrete Time Techniques for Time Delay Estimation[J]. IEEE Trans on Signal Processing, 1993, 41(2): 525-533.

[8] Rife D, Boorstyn R R. Single-Tone Parameter Estimation from Discrete-Time Observations[J]. IEEE Trans on Informaton Theory, 1974, 20(5): 591-598.

ResearchonAngleMeasurementMethodBasedon
TimeDifferenceofBroadbandSignalbyPassiveRadarSeeker

PANJin-bo1,DIHui2,ZONGJian3,HUTian-jun1

(1.Shanghai Institute of Electromechanical Engineering, Shanghai 201109, China; 2.Shanghai Institute of Satellite Engineering, Shanghai 201109, China; 3.Shanghai Radio Equipment Research Institute, Shanghai 200090, China)

Increasing signal bandwidth is the development trend of radar signal radiation source with the synthesis of the radar system. The wideband signal has the advantage of high accuracy of time difference estimation on account of large time-bandwidth product. The method of measuring the angle of passive radar seeker based on time difference estimation is studied based on this advantage. The Fourier transform is used to convert the broadband signal time difference estimation into frequency estimation to obtain higher accuracy. The expression of time difference estimation accuracy is deduced by theory and the expression of angle accuracy is obtained. The accuracy of time difference estimation is simulated for different signal bandwidth. The accuracy of angle estimation is simulated for different time difference

and different incident angle. The results show that this method can significantly improve the accuracy of the angle measurement respect to the interferometer angle measurement method without phase unwrapping.

passive radar seeker; angle measurement accuracy; time difference estimation; discrete Fourier transform

1671-0576(2017)02-0006-05

2017-03-25

潘金波(1985-)，男，工程师，主要从事制导系统设计(无线电)；狄 慧(1986-)，女，工程师，主要从事参数估计及无源定位。

TJ765.331

A