数字阵列雷达和差波束抗主瓣干扰研究

赵海军， 杨晓伟， 张璐辉

(西安艾索信息技术有限公司， 陕西 西安 710065)

数字阵列雷达和差波束抗主瓣干扰研究

赵海军， 杨晓伟， 张璐辉

(西安艾索信息技术有限公司， 陕西 西安 710065)

针对数字阵列雷达，当存在主瓣干扰时，用常规自适应波束形成方法进行自适应干扰对消，不但会引起主波束偏移和旁瓣电平升高等问题，还会导致期望信号也被抑制。为提升抗主瓣干扰性能，提出了一种基于和差波束降维的抗干扰方法。在接收端进行和差波束形成实现对接收信号的降维处理，再对降维后的信号进行干扰抑制。当存在多个干扰时，需要采用临近波束空间法进行差波束的自由度扩展。理论分析和计算机仿真表明，和差波束法相对常规自适应波束形成方法抗主瓣干扰性能更好，并且具有更好的鲁棒性。

数字阵列雷达； 主瓣干扰； 和差波束

0 引言

数字波束形成(Digital Beam Forming，DBF)技术，是针对阵列天线，利用阵列天线的孔径，通过数字信号处理在期望的方向上形成接收波束。当天线方向性具有自适应能力时，这种技术被称为自适应数字波束形成(Adaptive Digital Beam Forming，ADBF)[1]。

自适应波束形成取得广泛应用，特别是在雷达抗干扰方面。针对波束副瓣干扰的情况，传统自适应波束形成算法可以对干扰进行较好地抑制[2]。但是在日益复杂的电磁环境下，干扰很有可能从主瓣进入，此时常规自适应波束形成技术便暴露出两个缺陷：一是主瓣严重变形；二是旁瓣电平升高[3]。这都严重制约了自适应波束形成技术在实际工程中的应用。

解决主瓣波束变形的方法有对角加载，但是对角加载量难以控制，S. A.Vorobyov提出计算对角加载量实质上可以归结为 SOC 优化[4]，但计算量很大，并且无法得到明确的解析表达式，应用受到很大限制。当采样信号中混入期望信号时，用常规SMI方法求解[5]，会导致输出信干噪比降低，影响性能[6]。S. J. Yu 用阻塞矩阵方法克服估计协方差矩阵时信号的混入问题[7]，使得存在主瓣干扰时能保证主波束无畸变。上述方法都是先估计出数据的协方差矩阵，再利用特征分解或其它方法进行处理。但当同时存在一个或多个主瓣干扰时，上述方法的性能通常并不理想，会在干扰方向及期望信号方向均形成零点，对干扰进行抑制的同时也会抑制掉期望信号。

文献[8]提出一种依据阻塞矩阵预处理的自适应波束形成方法，该方法能够解决旁瓣电平升高和主波束变形的问题，但是缺点是需要精确估计主瓣干扰的方向。文献[9]提出一种基于特征空间正交投影预处理的自适应波束形成方法(EMP算法)，但是当主瓣干扰方向和期望信号方向较接近时，主波束的指向仍然会发生偏移，而且当空间中存在多个主瓣干扰时，该方法的空域滤波的性能将会严重下降。文献[10]提出一种基于大型辅助阵列的主瓣干扰的抑制方法，但由于其要求辅助阵列的孔径较大，严重影响其在实际中的应用。文献[11-14]介绍了极化滤波的主瓣干扰抑制方法，但是当存在多个极化方式不同的主瓣干扰时，该方法无法有效抑制干扰。

为提高抗主瓣干扰性能，本文针对数字阵列雷达，提出一种基于和差波束降维的抗干扰方法，在接收端通过DBF形成和差波束，对接收信号进行降维处理，然后对干扰进行抑制。

当存在多个干扰时，由于差波束数目需要大于等于干扰个数，所以采用临近波束空间法进行差波束的自由度扩展。仿真证明该方法抗主瓣干扰性能更好，并且具有更好的鲁棒性，可以广泛应用于工程。

1 信号模型

针对N个阵元的均匀线阵，阵元间距为d，天线波束指向为θ0，波束主瓣内存在一个目标和一个主瓣干扰，其角度分别为θs和θj，此时阵列雷达接收信号模型如图1所示，阵列接收到的信号可以表示为

x=a(θs)s(t)+a(θj)j(t)+n(t)

(1)

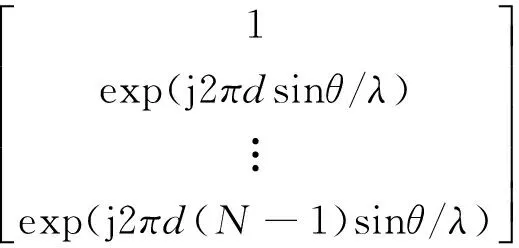
式中：a(θ)为阵列的导向矢量；s(t)和j(t)分别为目标信号和干扰信号；n(t)为均值为0。方差为σ2I的加性高斯白噪声，I为单位阵。

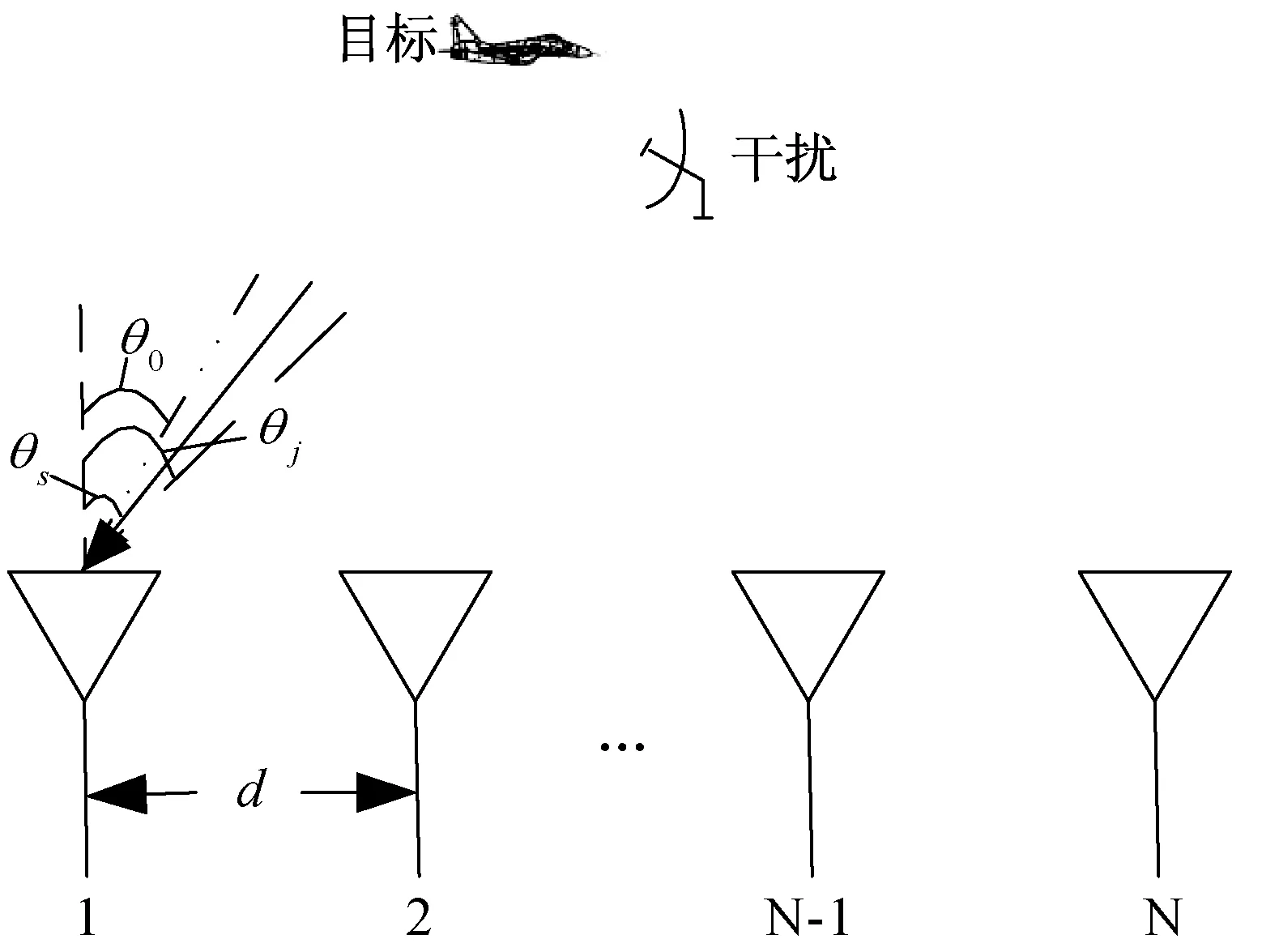
图1 均匀线阵接收信号模型

利用和差波束对接收信号进行降维，形成和差波束的权矢量分别为a∑和aΔ，其表达式分别为

a∑=a(θ0+δθ)+a(θ0-δθ)

(2)

aΔ=a(θ0+δθ)-a(θ0-δθ)

(3)

式中：δθ=θ3dB/2，θ3dB为当前波束指向的波束宽度。

在实际中，针对数字阵列雷达，也可以采用泰勒窗函数和Bayliss窗函数作为和差波束的加权系数[15]。

那么降维之后的信号可以表示为

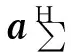
(4)

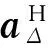
(5)

一般认为，目标方向更靠近波束指向，即|θs-θ0|<|θj-θ0|，那么此时可以进行加权滤除干扰，假设权系数为W，那么其表达式可以写成

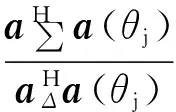
(6)

加权后的输出信号可以表示为

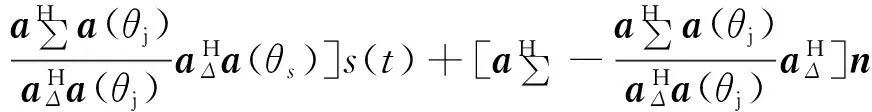
(7)

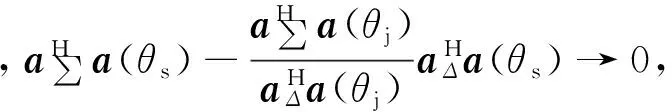
2 差波束自由度扩展

显然上述模型最多只能对消一个干扰，然而在主瓣内可能存在多个干扰，上述模型和方法不再适用，此时需要扩展差波束的自由度。假设主瓣内存在K个干扰，第k个干扰的角度为θjk。此时的信号模型可以表示为

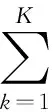
(8)

仍然采用和差波束的降维方法，和波束的权矢量与上述相同为a∑，此时需要合成多个差波束来扩展自由度，以对消干扰。采用临近波束空间法进行差波束扩展。

实际上是将差波束在主瓣宽度内进行平移，其表达式为

aΔk=a(θ0+Δθk+δθ)-a(θ0+Δθk-δθ)

(9)

式中：Δθk为第k个差波束零点位置，|Δθk|≤θ3dB/2。

针对K个干扰，需要K个自由度对干扰进行抑制，此时进行降维的矩阵T可以表示为

T=[a∑,aΔ1,…,aΔK]

(10)

那么降维后的信号可以表示为

(11)

根据最小均方误差准则，可以得到滤波权值为

(12)

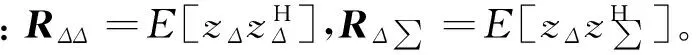
加权后的滤波输出信号可以表示为

WH[aΔ1,aΔ2,…,aΔK]Ha(θs)}s(t)+

(13)

3 计算机仿真

假设均匀线阵有32个阵元，阵元间距为半波长。本文方法简称为和差波束法(Sum and Difference beam, SD)。一般假设训练权值的样本中只包含干扰和噪声信号，这里我们考虑包含目标信号和不包含目标信号两种情况。

(1) 仿真一

假设空间中包含一个干扰，其角度为1°，干噪比为30 dB。目标角度为0°，信噪比为5 dB。此时只需要一个差波束就能够抑制干扰，此时差波束零点位置对准0°方向。取雷达间歇期的信号计算权值的样本，此时样本中只包含干扰信号。分析和差波束干扰信号的相关性随干扰角度的变化关系，如图2所示。

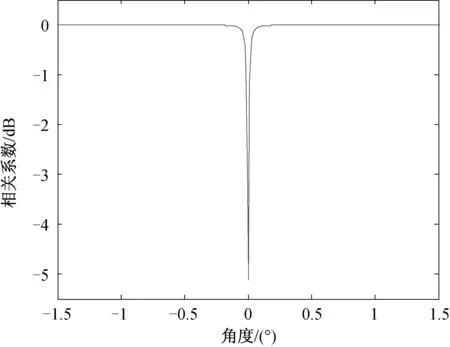
图2 和差波束干扰信号相关性随干扰角度变化关系

同时，分析输出信干噪比(SINR)随干扰角度变化的关系，并与全阵列的协方差矩阵求逆(SMI)算法进行对比，如图3所示。其中，不包含信号表示训练权值的样本中只包含干扰和噪声信号，包含信号表示训练权值的样本中包含目标、干扰和噪声信号。

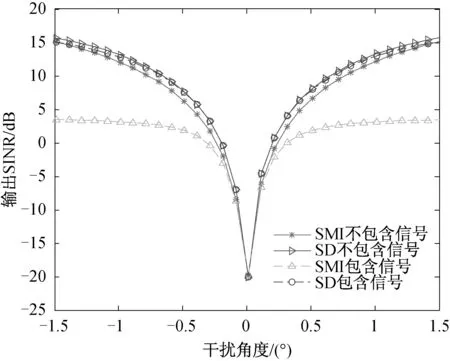
图3 干扰抑制效果随干扰角度变化关系

从图2可以看出，当干扰角度越靠近0°时，和差波束的干扰信号的相关性越差，对应图3中此时的干扰抑制性能越差。另外，当干扰角度越靠近零度时，和差波束法相对于SMI算法的提升不明显。而当干扰角度与目标角度较远时，此时和差波束法相对于SMI算法的提升很明显。

(2) 仿真二

空间中存在两个主瓣干扰，其角度分别为-1.5°和+1°，干噪比均为30 dB。目标角度为-0.5°，信噪比为5 dB。由于存在两个干扰，所以需要构造2个差波束。令其中一个差波束零深对准0°方向，另一个差波束需要进行平移构造。仿真分析输出SINR与第二个差波束零点位置的关系，如图4所示。

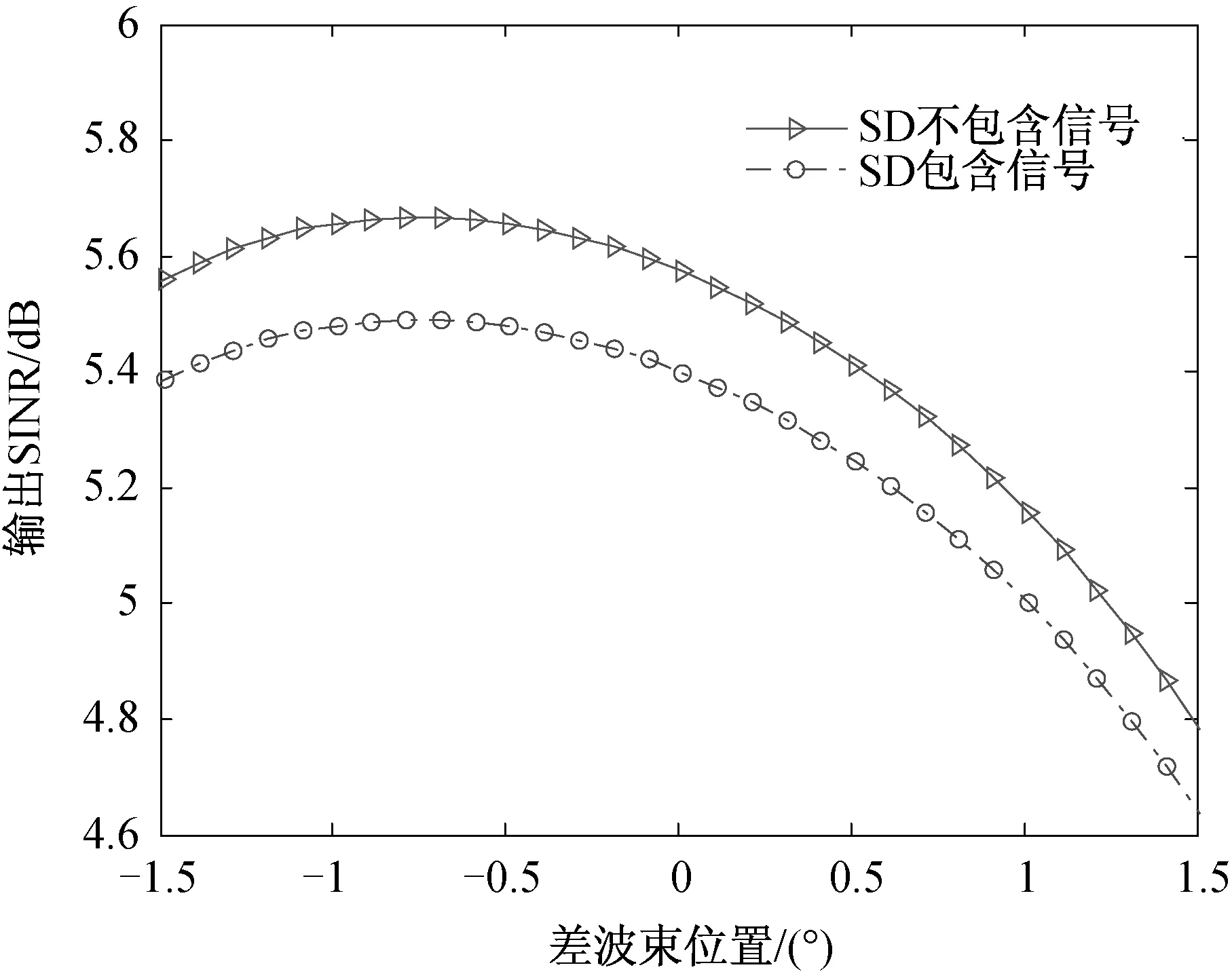
图4 输出SINR与第二个差波束零点位置Δθ关系

从图4可见，当第二个差波束零点位置越接近于目标方向时，取得的输出信干噪比越大，此时对抗主瓣干扰的性能越好。

(3) 仿真三

空间中存在两个主瓣干扰，其角度分别为-1.5°和+1°，干噪比均为30 dB。目标角度为0°，信噪比为5 dB。计算滤波输出信干噪比随快拍数变化，如图5所示。

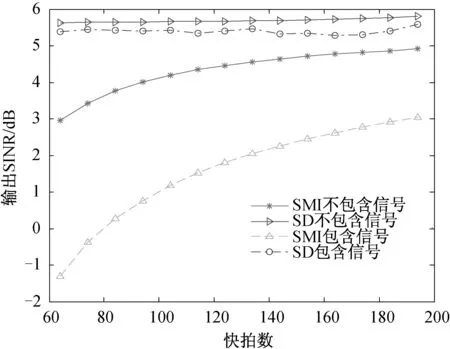
图5 滤波输出SINR随快拍数变化关系

从图5可以看出，随着快拍数的增多，四种情况的输出SINR都有一定程度的提升。当快拍数较少时，本文方法得到的输出SINR要比传统方法有6 dB左右的提升。可以发现，采用和差波束对抗主瓣干扰可以获得更好的性能。当训练权值样本中包含目标信号时，采用SMI算法的性能损失严重，而利用和差波束方法的损失较小，可以看出和差波束法具有更好的鲁棒性。

4 结束语

本文针对数字阵列雷达提出了一种基于和差波束降维的抗主瓣干扰方法。通过对接收信号进行和差波束形成对接收信号进行降维，然后再对降维后的信号进行抗干扰。相对于传统自适应波束形成方法，该方法抗干扰效果更好，有更好的鲁棒性，并且节省了计算量。本文所提方法可广泛应用于工程。

[1] 陈伯孝，朱伟，孙光才，等. 现代雷达系统分析与设计[M].西安：西安电子科技大学出版社， 2012： 56-58.

[2] Li Dan, Yin Qinye, Mu Pengchen, et al. Robust MVDR Beamforming Using the DOA Matrix Decomposition[C]. IEEE the 1st International Symposium on Access Spaces(ISAS). Dalian: IEEE Press, 2011: 105-110.

[3] Jablon N K. Adaptive Beamforming with the Generalized Sidelobe Canceller in the Presence of Array Imperfections[J]. Antenna Propagation, 1986, 34: 996-1012.

[4] Vorobyov S A, Gershman A B, Luo Z Q. Robust Adaptive Beamformingusing Worst-case Performance Optimization: A Solution to the Signal Mismatchproblem[J]. Signal Processing, 2003, 51: 313-324.

[5] Reed I S. Rapid Convergence Rate in Adaptive Antenna[J]. Aerospace and Electronic Systems, 1974, 10(6): 853-863.

[6] Chang L, Yeh C C. Performance of DMI and Eigenspace-Based Beamformers[J]. Antenna Propagation, 1992, 40(11): 1336-1347.

[7] Yu S J, Lee J H. Efficient Eigenspace-based Array Signal Processing Usingmultiple Shift-invariant Subarrays[J]. Antenna Propagation, 1999, 47(1): 186-194.

[8] 苏保伟, 王永良. 阻塞矩阵方法对消主瓣干扰[J]. 系统工程与电子技术, 2005, 27(11): 1830-1832.

[9] 李荣锋,王永良,万山虎.主瓣干扰下自适应方向图保形方法的研究[J]. 现代雷达, 2002, 24(3): 50-53.

[10] Yang X, Yin P, Zeng T, et al. Applying Auxiliary Array to Suppress Mainlobe Interference for Ground-based Radar[J]. IEEE Antennas Wireless Propagation Letters, 2013, 12: 433-436.

[11] Dai H, Wang X, Lin Y. Main-lobe Jamming Suppression Method of Using Spatial Polarization Characteristics of Antennas[J]. IEEE Transaction on Aerospace Electronic and System, 2012, 48(3): 2167-2179.

[12] 李金梁，罗佳，常宇亮,等. 基于天线空域极化特性的虚拟极化接收技术[J]. 电波科学学报， 2009， 24(3): 389-393.

[13] 刘勇，戴幻尧，李金梁,等. 空域虚拟极化滤波原理及实验结果[J]. 电波科学学报, 2011, 26(2): 272-279.

[14] 刘勇，梁伟，王同权,等. 基于空域极化捷变的有源假目标鉴别[J]. 电波科学学报， 2014, 29(2): 287-294.

[15] 朱伟，陈伯孝，周琦. 两维数字阵列雷达的数字单脉冲测角方法[J]. 系统工程与电子技术， 2011, 33(7): 1503-1509.

AMainLobeInterferenceSuppressionMethodBasedon
SumandDifferenceBeamforDigitalArrayRadar

ZHAOHai-jun,YANGXiao-wei,ZHANGLu-hui

(Xi’an iTHOR IT Co., Ltd. Xi’an Shaanxi 710065, China)

For digital array radar, if the interference falls into mainlobe, the desired signal would lose heavily when uses adaptive digital beamforming (ADBF) to eliminate the interference. At the same time, the adaptive pattern would have higher sidelobe and distorted mainbeams. A new interference suppression method based on reduced dimensions of sum and difference beam is proposed. The sum and difference beamforming are firstly carried out to reduce the dimensions of the

signal, and then the jamming suppression is performed. Under the multiple interferences scenario, multiple difference beams should be formed to expand the degrees of freedom. Compared with the ADBF, the proposed method has better performance and robustness for interference suppression.

digital array radar; main lobe interference; sum and difference beam

1671-0576(2017)02-0030-04

2016-12-10

赵海军(1982-)，男，硕士，工程师；杨晓伟(1983-)，男，硕士，工程师，均从事末制导雷达信号处理技术研究。

TN957.51

A