基于单天线波束扫描的解析测角方法
2018-07-14朱晓丹朱沛胜朱伟强曹雄宇
朱晓丹,朱沛胜,朱伟强,陈 卓,曹雄宇
(1.中国航天科工集团8511研究所,江苏 南京 210007; 2.中国科学院声学研究所,北京 100080)
0 引言
测角是雷达、导航、侦察的重要内容,目前高精度测角一般基于干涉仪或阵列体制,需要利用多个通道布置相对较长的基线,基线长度和通道的多少直接决定测角性能。对于小型无人机、微纳卫星等新型平台,受限于体积和功耗,通常难以负载多通道,且难以形成较长的基线。
利用旋转单天线进行角度测量仅需单个接收通道,且无需形成基线,是一种容易实现的方法[1]。按照观测量的不同,旋转单天线测角方法主要分为旋转多普勒测角和幅度比较法测角两类。受限于有限的旋转速度以及多普勒频率的测量精度,旋转多普勒测角方法精度一般较低;旋转单天线幅度比较法主要包括最大幅度法[1]、最小幅度法[2]、相邻波束比幅法、和差波束法等,由于幅度容易测量,利用定向天线进行比幅测角通常可以获得相对较高的精度,因而得到了广泛的应用。这类方法利用天线主波束/主瓣附近不同角度上增益的差异,测角精度直接受方向图主波束/主瓣宽度影响。为了提高测角进度,一般还需要对主波束/主瓣进行拟合,根据不同角度接收到的信号幅度的相对大小估计目标角度,这种处理方法容易实现,但也引入了误差,使得测角精度难以进一步提高。
为了实现旋转单天线高精度测角,文献[3~7]提出了最大似然估计方法,需要进行搜索求解,算法计算量大;文献[5]基于最大后验概率函数提出一种迭代解卷积方法,可实现超分辨率测角;文献[6]将旋转单天线测角问题转化为谱估计模型,并基于有限更新率采样理论,提出一种超分辨率估计方法,但需要通过零化滤波等方法求解,计算复杂度较高;文献[7]将天线看成是传输函数,接收信号功率则是天线方向图与观测角度的卷积,因而提出了一种基于傅里叶变换和解卷积的求法。尽管上述方法给出了目标角度的估计,但存在计算较复杂的问题,且通常将天线主瓣近似为二次函数,引入了模型误差,因此也难以实现高精度测角。
为了实现低计算复杂度的高精度测角,本文提出一种基于模式分量分离的测角方法。首先将天线方向图表示为指数和形式,通过模式分量分离,将角度估计模型转化为模式分量的估计,根据模式分量实现对角度的解析估计,同时结合多模式进行联合估计。估计算法不涉及搜索或复杂的矩阵运算,只涉及解析计算,因而计算量较小,易于工程实现。
1 问题模型
为了提高旋转单天线的测角精度,首先需要对天线方向图进行精确建模,记天线方向图为[6]:
(1)

(2)
式中,cm可通过天线的测试计算得到。在K个不同的方向接收同一测试信号,信号功率记为s(θk)(k=1,…,K),则有:
(3)


(4)
式中,“†”表示矩阵的伪逆。对角度为θ0的待估计目标,利用该旋转天线在N个不同观测角度φn(1≤n≤N)接收信号,假定在同样位置利用0 dB增益天线测量该信号得到的功率为P0,则在不同观测角度收到的信号功率可表示为:
(5)
即根据sn结合已知的天线方向图F(θ)估计目标角度θ0。
2 模式分量分离
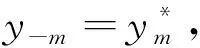
(6)
整理成向量形式为:
(7)
式中,
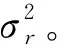
(8)
式(7)的求解需要满足N≥2M+1。同时可得估计误差的协方差矩阵:
(9)
3 多模式联合估计
3.1 基于单模分量的角度估计
(10)
由于相位具有模糊性,根据式(10)测角时将出现模糊。由式(10)可以看出,模糊为2π/m。进一步分析其估计误差,可得:
dθm=- (P0m)-1dy0+
(P0m)-1e-jmθ0dym
(11)
可求得:
e-jmθ0(E(drmdy0)+jE(dimdy0)))+
(12)
从而可求得角度估计误差的协方差矩阵Wθ,其元素(Wθ)mm′为:
(Wθ)mm′=
(Brrmm′+Biimm′+j(Birmm′-Brimm′))+
(13)
3.2 多模联合估计
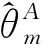
(14)
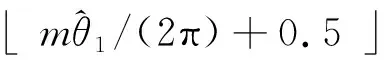
(15)
联合估计误差为:
(16)
4 理论估计误差分析
由式(5)得:
(17)
整理成向量形式为:
(18)
(19)

(20)
5 仿真分析
下面对本文提出的基于模式分量分离的测角方法进行仿真分析。天线量化为共计m=5个模式,随机产生的c0~c5为4.067、0.437、0.314、0.180、0.014、0.065。下面结合该天线进行仿真分析。仿真中,信号的平均功率P0为1。
5.1 模式分量估计误差分析
目标角度为3°,随机产生60个观测角度,进行500次Monte-Carlo仿真。不同信噪比下模式分量的估计误差如图1所示。可以看出不同模式分量的估计误差不相等,因此在测角时需要考虑模式分量估计误差的影响。
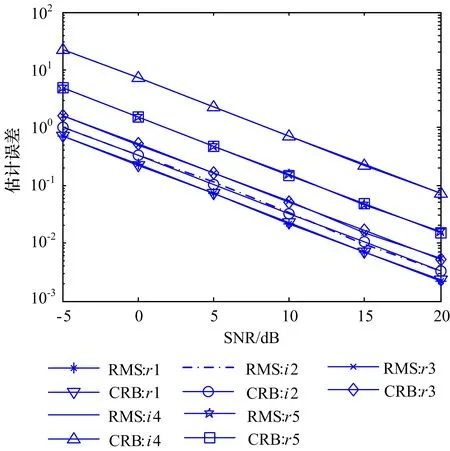
图1 不同信噪比下模式分量估计误差
5.2 多模联合测角分析
1)无模糊测角范围
不同模式分量对应的无模糊测角范围如图2所示。可以看出,无模糊测角范围与模式成反比,模式越

图2 不同模式分量对应的无模糊测角范围
大无模糊测角范围越小。通过低模式解高模式可进行联合测角,从而实现[-π,π]范围内的无模糊测角。
2)测角精度分析
在5.1节中的仿真条件下,不同信噪比下多模联合测角的误差及不同模式对应的单模估计的仿真,其中(模式1、3、5对应的单模估计误差未画出),模式2对应的单模估计精度最高如图3所示。模式4对应的单模估计精度最高;且联合估计精度优于各模式对应的单模估计精度,并能够达到模型理论估计精度。信噪比低于10dB时模式4对应的测角误差低于理论估计误差,这是因为此时测角出现模糊。

图3 不同信噪比下多模联合测角误差
不同角度对应的测角误差如图4所示。信噪比为10dB,其余仿真条件同于5.1节。可以看出在角度超过36°(π/5)时,由于出现测角模糊,测角误差较大;在无模糊测角范围内,不同角度对应的测角精度相等,因此角度大小不影响估计误差,这不同于干涉仪或阵列接近基线垂直方向测角精度高、接近基线平行方向测角精度低的特点,有利于实现全向高精度测角。
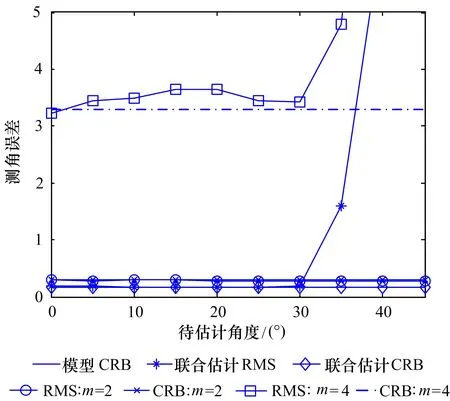
图4 不同角度对应的测角误差(SNR=10dB)
6 结束语
旋转单天线测角方法无需形成测角基线,且仅需单个接收通道,有利于减少系统设备规模,提高系统的适装性。本文提出的基于模式分量分离的多模测角方法只涉及解析计算,因而计算量较小;多模式联合测角具有精度高的优点,尤其适用于小型平台,实现高精度测角,具有十分广泛的应用前景。■
