基于ACA-SVD的雷达后向散射特性快速计算方法

郭良帅， 林 云， 梁子长， 高鹏程

(电磁散射重点实验室， 上海 200438)

基于ACA-SVD的雷达后向散射特性快速计算方法

郭良帅， 林 云， 梁子长， 高鹏程

(电磁散射重点实验室， 上海 200438)

雷达目标后向散射特性在工程设计中具有重要的作用，是实现雷达精确探测定位、识别的重要参数设计依据。基于电磁场理论的数值方法可准确计算目标后向散射特性。但在多角度后向散射问题中，以往的数值仿真算法在迭代计算每个后向散射角度时均单独开展计算，计算效率较低，无法满足工程设计需求。提出了一种基于自适应交叉近似(ACA)结合奇异值分解技术(SVD)的目标后向散射积分方程快速计算新方法，首先利用ACA算法计算、压缩右端激励矩阵，然后对压缩后的子矩阵进行二次压缩，进一步降低激励矩阵存储量和迭代求解时间，极大的提升雷达目标后向散射特性计算效率。

后向散射； 自适应； 近似算法； 奇异值分解

0 引言

雷达目标后向散射特性是实现目标精确探测、识别、定位的重要参数设计依据，尤其是工程应用中，雷达视线与目标相对姿态变化剧烈，单一或少量的后向散射角度无法提供目标准确的描述。通过仿真建模的方法提供目标后向散射特性信息是实现雷达设计的重要技术手段，可极大的节省研制成本，同时提供目标探测所需的理论验证数据。在目标后向散射快速计算方法中主要由以下几类：一是加速每个照射角度下的计算效率，如多层快速多极子(MLFMA)[1]、快速傅里叶变换(CG-FFT)、自适应积分方程(AIM)等，该类方法极大地提升了单个照射角度下的计算效率，但并未减少迭代求解的次数(及照射角度的个数)；二是基于模式降阶的方法，如模式参数估计(MBPE)、渐近波形估计(AWE)等，该类方法在小角度范围内具有明显的效果，但牺牲了部分计算精度；三是利用多角度照射矩阵方程右端项的线性相关性，利用低秩特性开展压缩计算，如QR分解方法、奇异值分解方法(SVD)、插值分解方法(ID)等，该类方法可减少矩阵迭代求解的次数，从而提升计算效率。

相比较而言，SVD、ID算法可利用矩阵的主奇异值特性，实现关键角度的最优选择，当后向计算角度较多且相关性较弱时具有较高计算效率。但该类方法需要预先计算处每个角度下的激励矩阵，从而需要较大的存储空间，影响了计算效率。本文研究基于ACA算法多后向散射激励矩阵的低秩压缩技术，然后利用SVD算法对ACA压缩得到的超定矩阵进行二次压缩，可减少计算复杂度和存储量。算例表明，本方法在保证求解精度的同时，可减少迭代求解时间和存储量。

1 基于积分方程的后向RCS计算

对于任意金属目标，根据电磁场理论和金属边界条件可得到频域散射场为

(1)

式中：k0为入射电磁波波数；A(r)为背景的磁场矢量位函数；j为虚数单位；r为空间位置矢量；为梯度算子；·为散度算子。通过目标离散和测试匹配过程[4]，可得到金属表面的矩阵方程

ZX(kinc)=B(kinc)

(2)

式中：Z是阻抗矩阵；B(kinc)是与照射角度相关的激励矩阵；X(kinc)是未知电流展开系数；kinc为入射电磁波传播矢量。对于未知量为n，探测角度为m的计算，B(kinc)是n行，m列矩阵。

一般而言，Z是无法直接求逆的，且其复杂度为O(N3)(N为目标表面离散的未知量个数)，需要逐个角度的开展迭代计算。极大的限制了积分方程求解问题的规模。目前，依据提出了多种加速阻抗矩阵求解的方法，如MLFMA将计算复杂度和存储复杂度降低为O(N×logN)，极大提升了积分方程的求解能力。但该类方法仅提升了单个角度下的求解次数。当m很大时，仍然无法满足计算需求。

2 自适应交叉近似算法

ACA算法的数学原理是利用矩阵元素的相关性对矩阵进行低秩压缩[2]，从而减少矩阵存储量和计算复杂度，分解形式如图1所示。

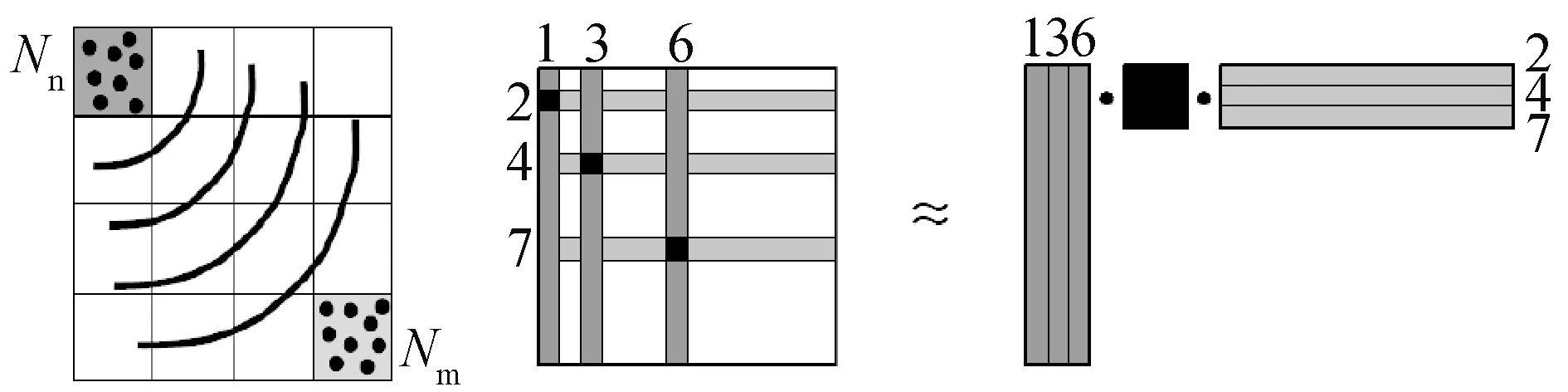
图1 ACA压缩形式

对于维数为n×m的矩阵Un×m，通过ACA分解可得到两个子矩阵An×r,Br×m(r为满足一定精度条件下的矩阵有效秩)。

Un×m≈An×r×Br×m

(3)

通过压缩得到的近似矩阵与原矩阵的近似程度可通过误差矩阵进行描述，表达式为

|Rn×m|≈|Un×m-An×r×Br×m|≤ε|Un×m|

(4)

式中：|Rn×m|为误差矩阵；|·|为矩阵的范数；ε为误差门限。对于超定矩阵、低秩矩阵的情况，r远小于m。只需进行r次迭代就可得到整个m角度下的后向散射特性。

ACA算法的存储复杂度为O[r(n+m)]量级，计算复杂度为O[r2(N+M)]量级。在ACA算法进行矩阵压缩时，并不需要将原激励矩阵Un×m全部计算出来并保存，可以在ACA分解时将对应的行或者列实时计算出来即可，有效地减少了计算量和存储量。通过对激励矩阵的低秩处理，矩阵方程的求解次数大幅减少。

3 奇异值分解技术

通过ACA压缩得到的子矩阵An×r不是正交满纸的，仍然可进行进一步压缩，SVD算法是实现该超定矩阵进一步压缩的有效技术手段。

矩阵u的奇异值分解表示为三个矩阵的乘积，即

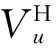
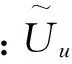
积分方程后向散射快速计算的实施步骤如下：

a) 首先利用ACA算法对式(2)的右端激励向量B(kinc)进行压缩，得到子矩阵u和v；

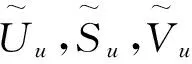
c) 针对式(2)中阻抗矩阵Z开展高效压缩计算(本文中利用MLFMA)；

4 数值算例

算例在Intel i7-3770 CPU上运行，内存为4 GB， ACA算法用OpenMP加速，利用MLFMA实现阻抗元素的加速求解。

(1) NASA杏仁核

数值算例选用NASA杏仁核，仿真示意图如图2。x，y，z为全局坐标系；u，v，n为局部坐标系，本算例中两者重合。计算频率为9 GHz，三角面元的剖分数目为13 744，未知量数目为20 611个，迭代收敛门限为0.001。

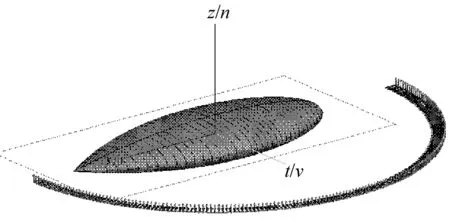
图2 NASA杏仁核仿真示意图

后向散射角度为θ=90°，φ=0°～180°，间隔1°，ACA和SVD的压缩门限为0.000 5。计算结果如图3。

图3 NASA杏仁核计算结果对比

图3结果显示利用ACA-SVD方法可得到较高的计算精度，计算精度在0.2 dBm2以内。本方法计算资源消耗如表1所示。

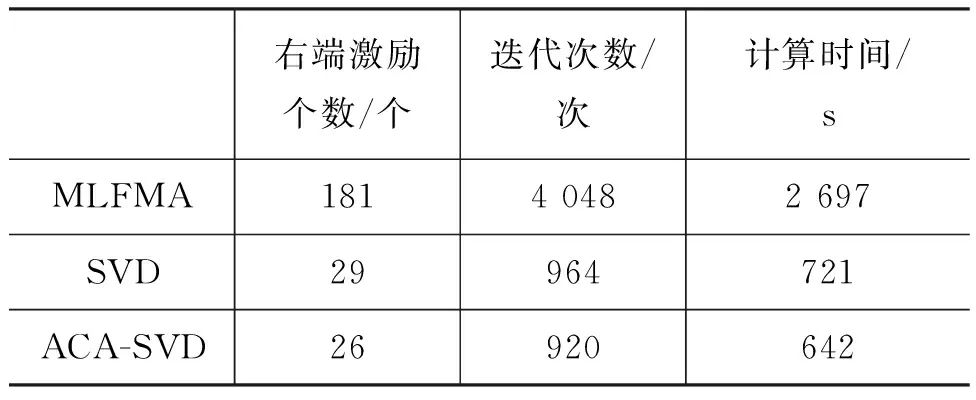
表1 NASA杏仁核计算资源对比

表1中可以看出，本文中所给方法可减少迭代次数和计算时间70%以上，仿真RCS与商业软件的均方根误差为0.8 dB。

(2) 腔体目标

选用腔体目标开展算法效率验证，腔体外轮廓为5 m ×5 m×5 m，壁厚为0.1 m，仿真示意图如图4所示。

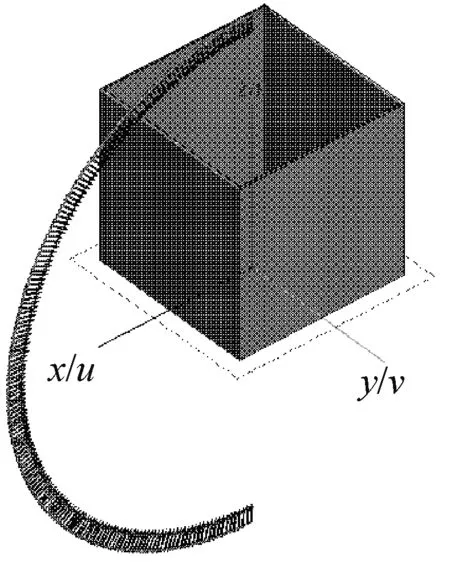
图4 腔体仿真示意图

仿真频率为3 GHz，后向散射角度为θ=0°～180°，Δθ=2°，φ=0°。后向散射截面计算结果如图5所示。计算结果同FEKO仿真结果吻合较好。

腔体目标的计算资源消耗如表2所示。

表2中可以看出，利用文中方法的计算时间仅为常规方法的30%左右，再次展示了文中所提方法的可靠性。

图6中给出了NASA杏仁核在超宽角度扫描范围内的后向散射计算结果，结果表明：本文研究方法将右端激励项个数由传统的91个缩减为20个，迭代次数由8 338个减少为2 046次，仿真RCS与商业软件的仿真结果均方根误差为0.3 dB。

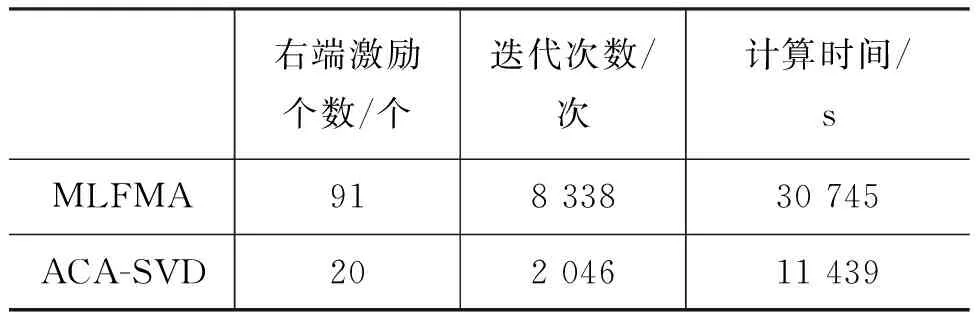
表2 腔体目标计算资源对比

5 结束语

研究基于ACA-SVD联合压缩的雷达目标后向散射截面，利用压缩后的子矩阵开展迭代计算，极大地减少了右端激励项个数和迭代收敛的次数。该方法理论依据充分，复杂目标的后向散射仿真计算结果表明了算法的正确性。通过与商业软件FEKO的资源消耗对比和结果对比，显示了算法的可靠性。

[1] Wei X C,Zhang Y J, Li E P. The Hybridization of Fast Multipole Method with Asymptotic Waveform Evaluation for the Fast Monostatic RCS Computation[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(2): 605-607.

[2] Zhi-Qing Lü, Xiang An. Fast Monostatic Radar Cross-section Computation for Perfectly Electric Conducting Targets Using Low-rankcompression and Adaptive Integral Method[J]. IET Microwave. Antennas Propag., 2014, 8(1): 46-51.

[3] Bebendorf M, Kunis S. Recompression Techniques for Adaptive Cross Approximation[J]. J. Integ. Equat., 2009, 21(3): 331-357.

[4] Arne Schröder, Heinz-D. Brüns, Christian Schuster. A Hybrid Approach for Rapid Computation of Two-Dimensional Monostatic Radar Cross Section Problems with the Multilevel Fast Multipole Algorithm[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(12): 41-47.

AFastRadarBackscatteringCalculationMethodBasedonACA-SVD

GUOLiang-shuai,LINYun,LIANGZi-chang,GAOPeng-cheng

(Electricmagnetic Scattering Laboratory, Shanghai 200438, China)

The radar backscattering character plays an important role in engineering design, which is the basis in radar detection and recognition. The numerical method is efficient to simulate the data. But in multi-angle backscattering problem, the numerical method need iterate every angle, which is inefficient, especially in multi-excitation situation. The ACA combined SVD method is presented to solve the backscattering problems based on integral-equation. Using ACA to calculate and compress the excitation matrix firstly, then the SVD is used to compress the sub-matrix, which can further reduce the memory and iterate time to develop the simulation of backscattering.

backscattering; adaptive; approximation algorithm; singular value decomposition

1671-0576(2017)02-0038-04

2016-03-15

上海市浦江人才计划资助(项目编号：15PJ1433300)、上海市青年科技英才扬帆计划资助(项目编号：15YF1411600)。

郭良帅(1988-)，男，硕士，工程师，主要从事目标反射、电磁逆反射技术研究。

TN955

A