一道2016阿塞拜疆奥赛试题下界再探

陈 宇

江苏省姜堰中等专业学校 (225500)

一道2016阿塞拜疆奥赛试题下界再探

陈 宇

江苏省姜堰中等专业学校 (225500)

文[1]中，对一道2016阿塞拜疆奥赛试题：

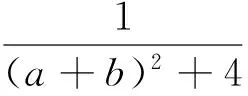
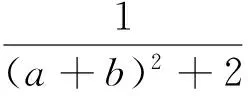
经过一番探究，笔者发现，不等式(3)可继续推广且存在统一的下界.即

定理3 已知a,b,c是满足ab+bc+ca=3的正数，λ>0，则

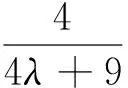
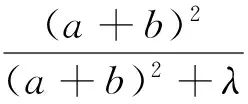
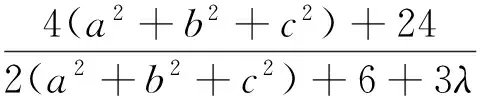
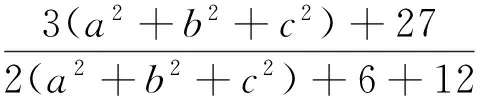
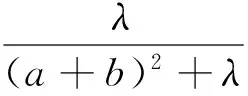
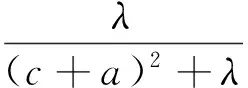
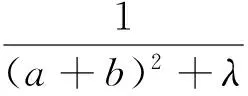
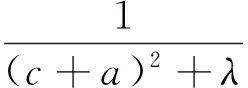
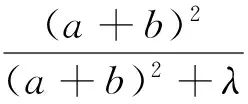
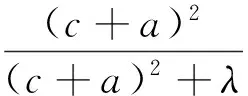
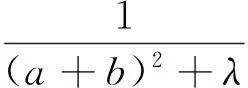
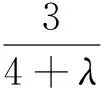
文[1]已证明，当λ≥2时，不等式(4)右边成立.

由此可知，定理3即不等式(4)右边成立.

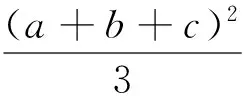
不等式(4)左边⟺(4λ+9)[(a+b)2(b+c)2+(b+c)2(c+a)2+(c+a)2(a+b)2]+(8λ2+18λ)[(a+b)2+(b+c)2+(c+a)2]+12λ3+27λ2>4(a+b)2(b+c)2(c+a)2+4λ[(a+b)2(b+c)2+(b+c)2(c+a)2+(c+a)2(a+b)2]

+4λ2[(a+b)2+(b+c)2+(c+a)2]+4λ3⟺9[(a+b)2(b+c)2+(b+c)2(c+a)2+(c+a)2(a+b)2]+(4λ2+18λ)[(a+b)2+(b+c)2+(c+a)2]+8λ3+27λ2>4(a+b)2(b+c)2(c+a)2(5).

由上可知(5)左边>36(a+b+c)2(∵λ>0时，4λ2+18λ>0,8λ3+27λ2>0)

∴要证(5)成立，只需证9(a+b+c)2>(a+b)2(b+c)2(c+a)2,只需证3(a+b+c)=(ab+bc+ca)(a+b+c)>(a+b)(b+c)(c+a).

上式两边整理后得abc>0成立(∵a,b,c>0,).从而不等式(4)左边成立.

笔者猜想，进一步，不等式(4)推广为

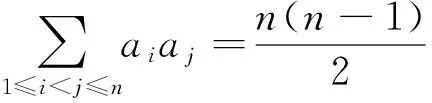
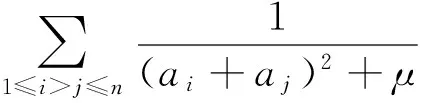
(6)也应存在下界，然囿于自身的知识和能力，笔者无力确定不等式(6)理应存在的下界，遑论证明该下界.还望方家及爱好者不吝赐教.不失为引玉之法.

[1]王潇轩.2016阿塞拜疆奥赛试题下界的下界估计[J].中学数学研究(江西),2017,4.