例析数学学习中的直觉思维培养

庞良绪

上海市市西中学 (200040)

例析数学学习中的直觉思维培养

庞良绪

上海市市西中学 (200040)

数学直觉思维是指人们不受固定的逻辑规则约束,对数学对象(结构及其关系)的某种直接领悟和洞察,它是人们运用已有的知识组块和形象直感,对当前问题进行敏锐的观察,细致的分析,透彻的理解,并能迅速发现解决问题的方向或途径的一种思维形式.

作为科学探索能力，直觉显然是十分重要的，这正如数学家庞加莱所指出的：“逻辑是证明的工具，而直觉则是发现的工具.” 那么，数学学习也需要直觉吗？“一个悬而未决的难题，几年来苦苦地在我脑海中反复盘旋.两天之前我成功了……谜在一瞬间解开，像闪电一样！我自己也说不清是什么导线，把我原先的知识和使我成功的东西连结了起来”.这是“数学王子”高斯在兴奋地讲述自己在一次重要突破中的体验.这就是人类创造性思维中一朵神秘之花:灵感.身无彩凤双飞翼，心有灵犀一点通.庞加莱也指出：“直觉……对有创造性的科学家来说，是须臾不可缺的.”为此，加强数学直觉思维的培养，对培养学生的数学创造性思维是不可缺少的.

本文试从以下几个方面探析数学直觉思维的培养.

1.追求美感，诱发直觉思维

数学教育的目的之一就是应该让学生获得对于数学美的鉴赏能力，这不仅有利于激发学生对数学的爱好，也有助于学生数学直觉思维能力的提高，感觉不到数学的美与优雅，就不会有数学直觉的产生，法国数学家阿达马曾指出：发明就是选择，而选择则唯一地是由科学美感所支配的，数学直觉的本质是某种‘美感’或‘美的意识’，美的意识越强，发现和辩证隐蔽的和谐关系的直觉也就越强.

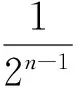
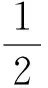
分析：观察题目中条件与结论之间的结构后会发现：在a,b,c是任意值时等式是不成立的，从而在a,b,c之间存在比条件更简洁的关系；作为特例考虑，显然三个数有两个数互为相反数时，条件与结论均成立，这意味着条件式子含有因式(a+b)或(a+c)或(b+c)，由于轮换对称性，则必含有因式(a+b)·(a+c)·(b+c).于是数学直觉形成，只需化简至既定目标即可推得结论.这个直觉来源于条件式子的轮换对称美，和谐美.这也来源于对题目条件的直觉.

2.类比联想，激发直觉思维

类比是根据两个或两个以上的对象之间某些方面的相似或相同，从而推断出它们在其它方面的相似或相同的一种逻辑推理方法，数学模型方法是类比在数学中得到广泛应用的一种形式，通过类比，迅速构建数学模型，将大脑中储存的知识信息进行加工，形成思维组块，从而启迪思维，促使直觉产生.

案例4 求证:10092017>2017!.

这些解题中突然涌现出来的“灵机”，就是直觉的表现.相信每个数学学习者都希望自己多拥有一些这种才能.

应该指出，这种迅速识别、直接证明、综合判断的“数学洞察力”并非天生的，而恰恰是学习者数学素养的一种集中反映.扎实的数学基础知识，灵活的变通思维能力，一定时间的冥思苦想加上适当的激发情境(如心情好，与别人进行研讨，触景生情等)，“直觉”也会垂青于你的.

请注意，别忘了记下自己产生“直觉”时的感受，因为，这还是一个值得深入研究的有趣的课题.

3.大胆猜想，构建直觉思维

猜想是一种合情推理，对于未给出结论的数学问题，猜想的形成有利于解题思路的正确诱导.对于已有结论的问题，猜想也是寻求解题思路策略的重要手段，数学猜想是有一定规律的，并且要以数学知识和经验为支柱，而培养敢于猜想，善于探索的思维习惯是形成数学直觉，发展数学思维，获得数学发现的基本素养.按照学生的认识发展规律，儿童阶段的直觉思维在整个的思维活动过程中占有主导地位，但随着年龄的增大，受到的挫折和伤害增多，直觉思维渐渐受到了抑制.事实上，直觉思维既容易由于受到鼓励使之得到发展，也极易受到伤害而被扼杀，因此在教学活动中，要发展学生的直觉思维能力，就要鼓励学生大胆猜想.

当然，直觉得到的结果也可能不完善，也可能是错误的，这时，还应与逻辑思维相结合，以导向正确的证明和演算.

案例6 曲线C:y=x2,有一条长为m的线段两端在C上滑动,求它的中点纵坐标的最小值.

直觉继续猜想,这条长度一定的线段两端在抛物线上滑动,滑动…,它滑动时,中点坐标的改变只与直线的倾斜程度有关,可以用倾斜角作为中间变量.用分析思维验证直觉猜想估计的结果:

4.观察特征，引发直觉思维

直觉思维是把问题当作一个整体来分析，从全局出发，观察其特征，避开具体细节的逻辑分析，直观洞察，领悟本质，迅速产生解题思路.

案例7 已知x,y满足x≥1,y≥1及(logax)2+(logay)2=loga(ax2)+loga(ay2) (a>0且a≠1)，当a∈(1,+∞)范围内变化时，求loga(xy)的最值.

分析：由于已知条件的数量关系不够明朗，观察其结构特征，为使复杂的关系简单化，直觉思维告诉我们采用换元法.

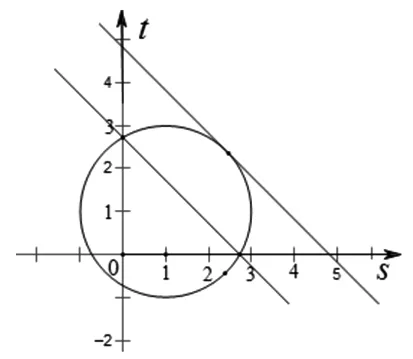
图1

令s=logax,t=logay(s≥0,t≥0) ，题设条件转化为(s-1)2+(t-1)2=4,(s≥0,t≥0)表示圆在第一象限内的一部分(如图1).而所求loga(xy)=s+t，令s+t=k，则联想为直线，k为截距.

直觉思维是数学发现的关键因素,是逻辑的飞跃和升华,是人脑对数学对象及其结构敏锐的想象.直觉的领悟,迅速的判断,是数学的洞察力.重视发展学生的数学直觉思维能力有利于创造型人才的培养，在数学教学中将直觉思维与逻辑思维有机地结合、相互补充，才能相映成趣、取得成效.至于怎样培养自己的直觉能力，贝弗里奇提出过一些好的建议，诸如：对问题作长时间的思考，紧张思考后的“悠闲放松”，与别人交流，随时记下思维的“闪光 ”……