始于“偶然” 终于“精彩”——一次“意外涂鸦”引发的命题探究

蔡勇全

四川省资阳市外国语实验学校 (641300)

始于“偶然” 终于“精彩”
——一次“意外涂鸦”引发的命题探究

蔡勇全

四川省资阳市外国语实验学校 (641300)

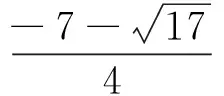
图1

观察图像的走势不难发现，两个图像“扭作一团”，呈麻花状，笔者喜出望外，这不正是创造分段函数的极好素材和契机吗?经过构思，得到了第一个分段函数f(x)=

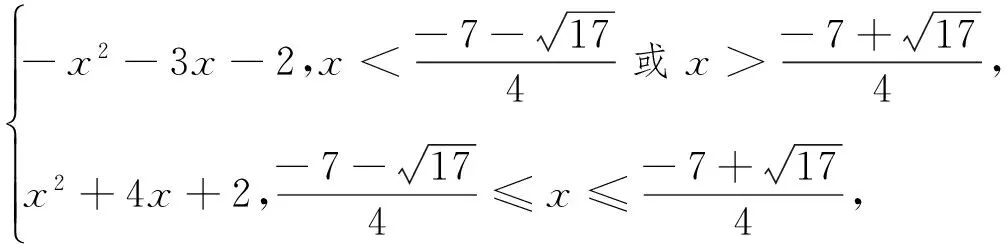
(1)已知函数f(x)=

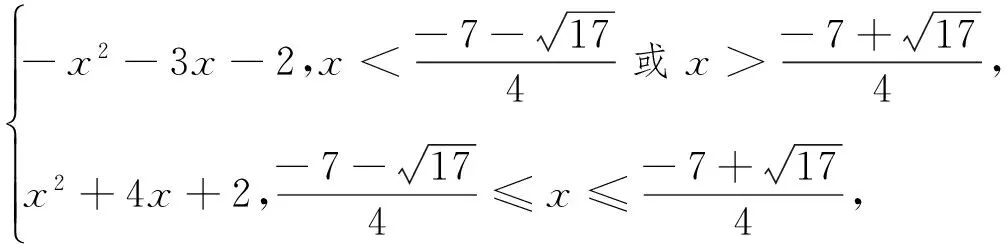
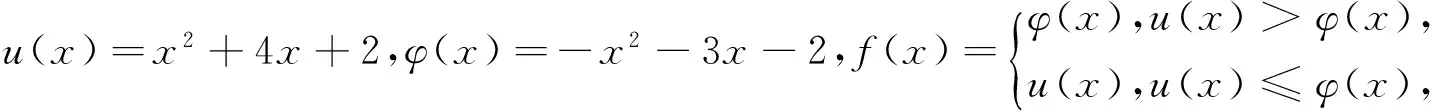
尽管两个题目均为“双层最值问题”，但似乎有些普通，新意不足，不妨引入新定义，从内容方面进行创新，让其成为创新型题目，考查学习潜力，因此得到:

题目1 定义:{r，s}min指r、s中较小者.记f(x)={x2+4x+2，-x2-3x-2}min，则函数f(x)的最大值为___________.

题目2 定义:{r，s}max指r、s中较大者.记g(x)={x2+4x+2，-x2-3x-2}max，则函数g(x)的最小值为___________.

题目1与题目2均属于从内容方面进行创新的类型，从内容方面进行创新指题目中首先引入新的定理、运算、规则、概念、符号等，解题之前需要先理解这些新内容的实质，再结合过去学习过的知识加以解决.内容创新的方式多种多样，同样的含义，有不同的定义方式，如题目1与题目2的等价创新形式分别是:

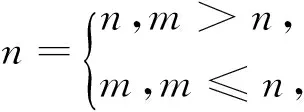
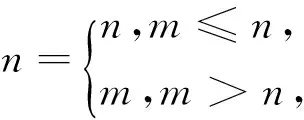
题目3、4仍属于“双层最值问题”，“※”是命题时随意撷取的一个符号而已.另外，分段函数与常数函数往往被视为一对孪生兄弟，二者经常被放在一起研究交点、实根、零点的个数问题，结合各顶点、端点处的函数值情况，可以产生:

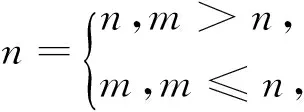
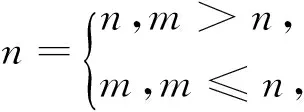
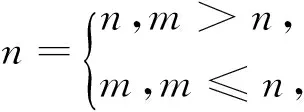
题目5、6、7的实质是在函数y=f(x)与常函数固定的情况下，回答二者交点的个数问题，如果把常数位置换成参数，并指出交点、根、零点的具体个数，探求参数的取值范围，又将怎样呢？也就是从题目形式方面对设置问题的方式进行创新，编拟逆向探索创新性问题.

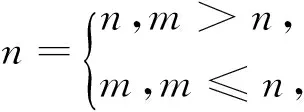
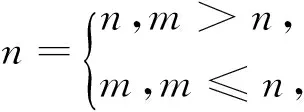
上述创新型题目中所涉及到函数f(x)或g(x)均为连续函数，如果在m、n的关系上面作调整，让函数图像断开，增加思维量，减少运算量，又该如何设计呢？这就只能从m与n的关系着手，于是得到题目10:

题目10的诞生恰到好处地契合了“多考点想，少考点算”的命题指导原则.

事实上，根据图像特征，在同样定义新运算的前提下，如果仅考虑m、n的大小所导致的取舍问题，以抛物线之外的其他素材为背景，还有许多命题结合点，还可编制若干创新型题目，比如可以把新运算与三角函数、导数、平面向量、不等式恒成立问题等话题联系起来，如题目11:

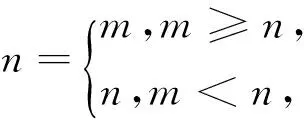
新的运算在中学教材中可能未曾出现，也有可能在整个数学知识体系中并不存在，但这并不重要，我们命题时也不必刻意在乎新运算的存在性，即便新运算可能是杜撰出来的也未尝不可，因为新的运算在题目中仅仅起着抛砖引玉或工具性的作用，所用的解题策略仍是平常所见的通性通法，这样的题目注重检测信息迁移能力、学习能力、接受新生事物的能力.

最后，笔者想说的是，一次涂涂画画的无意之举，酿就了一系列优美、新颖、启智的好题，是笔者所始料不及的，但同时以上命题过程明白无误地告诉我们，学习与生活中存在着很多可用于命制新题目的元素，有时不一定非得要刻意搜寻，可能一次无心插柳之举就会得到意想不到的命题素材，许多很常见甚至不起眼的材料，也许皆能以此为基点命制出冲击思维和视角感官的新题目，所谓“真理本天成，慧眼偶得之”就是这个道理，所以我们应做学习、生活的有心人，要留意生活，留心身边时常见到的各种素材，日积月累，注意总结，善于联想，这是一个“把书变厚、把书变薄”的先后过程，在这一过程中，要多思考，多反省，这样，我们的命题能力才会日渐增长，命制题目所需要的素材才能信手拈来，才会命制出高质量的题目.