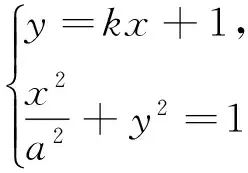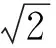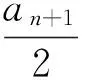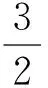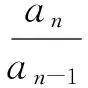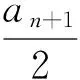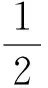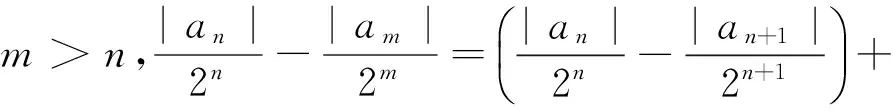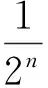“简洁、初等、本源”2016浙江(理)高考数学试题印象
2017-11-02潘建伟虞关寿
潘建伟 虞关寿
浙江省绍兴鲁迅中学 (312000)
“简洁、初等、本源”2016浙江(理)高考数学试题印象
潘建伟 虞关寿
浙江省绍兴鲁迅中学 (312000)
2015年与2016年这两年浙江数学高考有点特殊,这两年的数学高考的考查内容与形式与以往和以后数学高考在内容与形式上有所不同,这使得这两年的高考试题尤为令人关注,高考之前扑朔迷离,总有许多的猜测,高考之后甜酸苦辣总有许多感慨.笔者阅读了这份试卷,并认真演算了一番,感觉到这份试卷与以往的高考试题在考查知识能力,及方法上符合考纲要求,承延了以往高考试题的风格与特点,但这份试卷又有自已独特的个性,给笔者印象颇深的是六个字:简洁、初等、本源.下面具体展开,与同行商讨,一家之言,谨请批评指正.
一、简洁
浙江数学高考卷与其它省市的高考试卷相比,从外观上一个显著的特征是“简洁”.试题设计简洁,题干语言简洁,不过多浪费考生的阅读时间.今年的高考试题不但试题外观简洁,题干语言简洁,更值得推崇的是考题中呈现的所有图形简洁明了,这是区别于以往考题的明显特点,不论是立体几何的图形,还是解析几何的图形,呈现给考生的是一目了然,清晰意会的图形,图形中线条较少,且都是涉及图形面上、形上的问题.

A.m>n且e1e2>1
B.m>n且e1e2<1
C.m
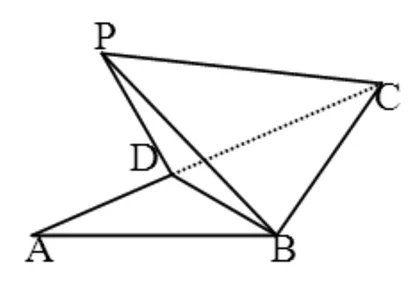
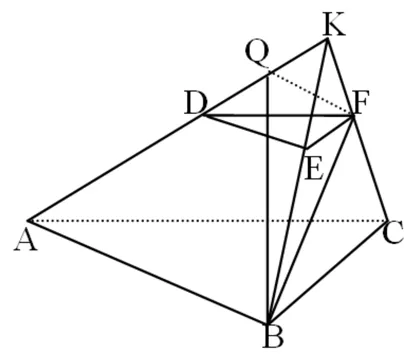
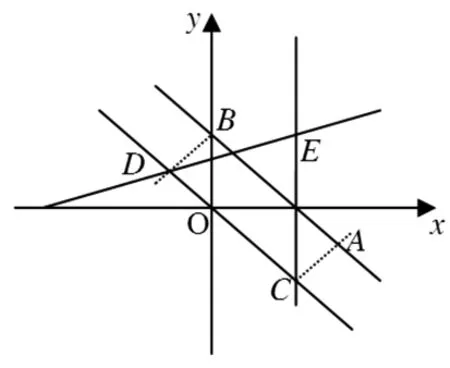
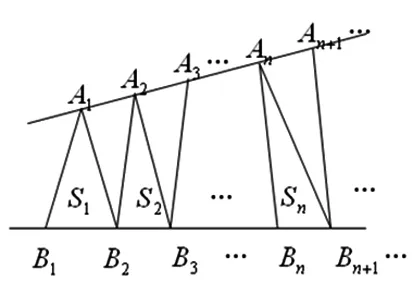
D.m 例2 (第14题)如图1,在ΔABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是________. 图1 解析:本题考查空间几何体及其体积的求法等知识,意在考查学生的空间想象能力、推理论证能力和运算求解能力.本题所给的图形清楚简单朴素. 由AB=BC=2,∠ABC=120°,可得AC= 例3 (第16题)在ΔABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB. (1)证明:A=2B; 解析:把三角恒等变换与解三角形结合起来是近几年高考考查的主要形式与内容,但考查核心依旧是三角恒等变换、正弦定理、余弦定理、三角形内角和定理及三角形面积公式.该题设计简洁,题意清楚明了.在解决此题时易抓住问题的本质,能选好公式快速解决. (1)∵b+c=2acosB,由正弦定理得sinB+sinC=2sinAcosB,故2sinAcosB=sinB+sin(A+B)=sinB+sinAcosB+cosAsinB,于是sinB=sin(A-B).又A,B∈(0,π),故0 图2 例4 (第17题)如图2,在三棱台ABC-DEF中,平面BCEF⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3. (1)求证:BF⊥平面ACFD; (2)求二面角B-AD-F的平面角的余弦值. 解析:本题图形简单,所给的条件与所要求的结论都在面上,所要添加的辅助线也不多.本题主要考查线面垂直的证明、二面角的计算等基础知识,同时考查学生的空间想象能力和运算求解能力. 图3 (1)延长AD,BE,CF相交于一点K,如图3所示.∵平面BCFE⊥平面ABC,平面BCFE∩平面ABC=BC,且AC⊥BC,∴AC⊥平面BCK,∴BF⊥AC,又EF∥BC,BE=EF=FC=1,BC=2,∴ΔBCK为等边三角形,且F为CK的中点,则BF⊥CK,又∵AC∩CK=C,∴BF⊥平面ACFD; 注:第(2)题也可用空间直角坐标向量解决. 在高考之前,我们所进行的专题复习中,可能会热衷于搞好一些与高等数学相关联或以高等数学为背景的题,我们在各种高考模拟考题中总能看到这类题,但从今年的高考试题一扫这类题目,反而增多了背景“初等”的题目,比如考几何多以三角形的背景的图形、考函数多以二次函数为背景、考数列多以等差等比数列为背景等.难怪,2016年高考之后,许多老师感慨这一年高三复习又白复习了,复习方向走偏了,这值得我们来年高三复习深思.下面例举几题并作适当的评说. 解析:本题主要考查了不等式组表示的平面区域、两点间的距离公式、投影等基本知识,通过这些初等知识的考查,意在考查学生的转化与化归、数形结合的数学思想. 图4 作出不等式组所表示的平面区域如图4中的ΔCDE,过C、D分别作直线x+y-2=0的垂线,垂足分别为A、B,则四边形ABDC为矩形,又C(2,-2),D(-1,1), ∴|AB|=|CD|= 例6 (第6题)如图5,点列{An},{Bn}分别在某锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*;|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*(P≠Q表示点P与Q不重合).若dn= |AnBn|,Sn为ΔAnBnBn+1的面积,则( ). A.{Sn}是等差数列B.{S2n}是等差数列 C.{dn}是等差数列D.{d2n}是等差数列 图5 解析:本题考查等差数列的概念、平行线的性质等初等基础知识,意在考查学生分析问题和解决问的能力. |BnBn+1|×hn,|BnBn+1|为定值,所以{Sn}是等差数列.故选A. 例7 (第13题)设数列{an}的前n项和为Sn.若S2=4,an+1=2Sn+1,n∈N*,则a1=________,S5=___________. 解析:本题主要考查等比数列的概念、通项公式,通项与前n项和之间的关系等基础知识,意在考查学生的基本运算求解能力、分析问题的能力和解决问题的能力. (1)求使得等式F(x)=x2-2ax+4a-2成立的x的取值范围; (2)①求F(x)的最小值m(a);②求F(x)在区间[0,6]上的最大值M(a). 解析:本题涉及二次函数、二次不等式等基础知识,主要考查函数的单调性、最值等基本性质,同时考查了学生的推理论证、分析问题等基本能力.处理函数问题,数形结合和分类讨论是最常用和最基本的思想方法,准确地画出图像可以规避许多冗长的计算,所以从最基本的方法着手,可直至问题的核心.最值函数是浙江省高考的特色,利用max函数、min函数可让分类讨论更简捷. (1)由于a≥3,故当x≤1时,(x2-2ax+4a-2)-2|x-1|=x2+2(a-1)(2-x)>0;当x>1时,(x2-2ax+4a-2)-2|x-1|=(x-2)(x-2a).∴使得等式F(x)=x2-2ax+4a-2成立的x的取值范围为[2,2a]. (2)①设函数f(x)=2|x-1|,g(x)=x2-2ax+4a-2,则f(x)min=f(1)=0,g(x)min=g(a)=-a2+4a-2,∴由F(x)的定义知m(a)= min{f(1),g(a)},即 ②当0≤x≤2时,F(x)=f(x)≤max{f(0),f(2)}=2=F(2);当2≤x≤6时,F(x)=f(x)≤max{g(2),g(6)}=max{2,34-8a}= max{F(2),F(6)}. 2016年的浙江高考试题给我们有这样的一个共同感受:运算量明显减少,思维量增大,好多题不是靠“算”能够解决的,感觉到“有力使不进去”,考查数学概念化的东西明显增多,试卷的“数学味”增浓了.可能这也是我们高三复习所要重视的问题,我们应更加关注数学本源的东西,让学生明白所学的知识内容“源头”是什么,为什么要学,学了又有何用.比如说什么是函数?函数的本质是什么?学习数列,我们到底要培养哪种素能?又比如说,碰到绝对值问题,我们第一反应是如何脱绝对值符号,那如何去脱呢等. 例9 (第5题)设函数f(x)=sin2x+bsinx+c,则f(x)的最小正周期( ). A.与b有关,且与c有关 B.与b有关,但与c无关 C.与b无关,且与c无关 D.与b无关,但与c有关 解析:本题主要考查三角恒等变换、三角函数的最小正周期等基础知识,其本质上主要考查了形如“y=Acos(ωx+φ)+B”的周期公式. 例10 (第8题)已知实数a,b,c. A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100 B.若|a2+b+c|+|a2+b-c|≤1,则a2+b2+c2<100 C.若|a+b+c2|+|a+b-c2|≤1,则a2+b2+c2<100 D.若|a2+b+c|+|a+b2-c|≤1,则a2+b2+c2<100 解析:本题给学生的感觉是选择题的压轴题很难,从正面去化解绝对值符号,的确较难,但该题的考查本意是看考生能不能找到适合的“反例”去破解问题,这是该题本源的东西. 取a=10,b=10,c=-110,可排除选项A;取a=10,b=-100,c=0,可排除选项B;取a=10,b=-10,c=0,可排除选项C.故选D. 图6 (1)求直线y=kx+1被椭圆截得的线段长(用a,k表示); (2)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围. 解析:解析几何重点考查圆锥曲线的方程、几何性质、直线与圆锥曲线的位置关系以及与圆结合的综合问题等.本题就考查了这个本源的内容,第(1)问只要联立方程,利用弦长公式即可求得;第(2)问先假设圆与椭圆的公共点有4个,利用|AP|=|AQ|,求得a的取值范围,进而得到满足题目要求的a的取值范围,从而求得离心率的取值范围. (2)假设圆与椭圆的公共点有4个,由对称性可设y轴左侧的椭圆上有两个不同的点Ρ,Q,满足|ΑΡ|=|ΑQ|.记直线ΑΡ,ΑQ的斜率分别为k1,k2,且k1,k2>0,k1≠k2. 例13 (第20题)设数列{an}满足|an- (1)证明:|an|≥2n-1(|a1|-2),n∈N*; ∴|an|≥2n-1(|a1|-2),n∈N*. 综上,对于任意n∈Ν*,均有|an|≤2,n∈N*.




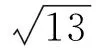
二、初等
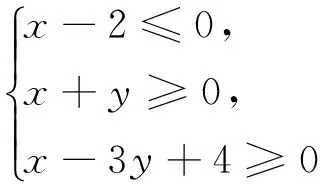


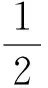
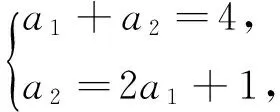

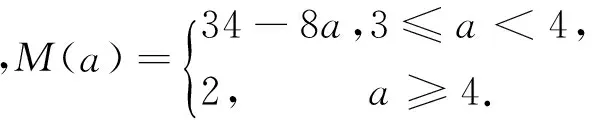
三、本源