用“嵌入法”解决三视图还原直观图问题

杨昌座

福建省南安市第三中学 (362300)

用“嵌入法”解决三视图还原直观图问题

杨昌座

福建省南安市第三中学 (362300)

近几年全国课标卷对“三视图”问题的考查一直是个“热点”，它是考查学生空间想像能力的一个重要载体.其中“三视图的还原”比起“画出物体的三视图”难度更大，前者对空间想象能力的要求更高，这需要学生熟练掌握直观图和三视图两者之间的联系，能根据条件作出正确的图形，根据图形想象出直观形象.特别是在2014年数学理科课标Ⅰ卷第12题后，大伙对三视图还原问题有了进一步的探究与思考，现笔者介绍一种解决这类问题的有效方法——“嵌入法”.

首先，三视图是观测者从上面、左面、正面三个不同角度观察同一个空间几何体而画出的图形，它是几何体从不同角度正投影后的平面图，因此具有“正视图和俯视图一样长，正视图和侧视图一样高，侧视图和俯视图一样宽的特征，也就是“正俯长、正侧高、侧俯宽”.

高中阶段所接触的三视图相对简单，大多数通过对长方体或者正方体进行切割而成，或者是圆锥(或圆柱)与长方体(或正方体)的组合，因此我们对一些基本的几何体的三视图应该熟练掌握，例如，三棱锥，三棱柱，圆柱，圆锥，四棱锥，四棱柱等.一般情况下，我们知道：

(1)如果三视图中有两个或三个三角形，那么这个几何体一定是棱锥；

(2)如果三视图中有两个或三个四边形，那么这个几何体一定是棱柱；

(3)如果三视图中有一个圆，那么这个几何体可能是圆柱或圆锥等旋转体.

当我们对这个几何体初步的形状确定后，遇到求体积等基本问题时，就容易解决，但如果是求表面积、最长棱等问题时，这就需要知道其各个面的情况，也就是将三视图还原成直观图问题，那么对于这类难度较大的问题有没有一种好的方法呢？在此介绍一种方法——“嵌入法”，它是根据三视图，把三个视图嵌入到我们熟悉的几何体中，例如：长方体或正方体，通过确定其顶点的位置后，连接各条棱，然后再把多余的线擦掉，即能画出所要求的几何体.即我们只需要在长方体(正方体)中找到这个几何体的顶点即可.在这一过程中，需要注意“正俯长、正侧高、侧俯宽”的特征及三视图中的实、虚线.

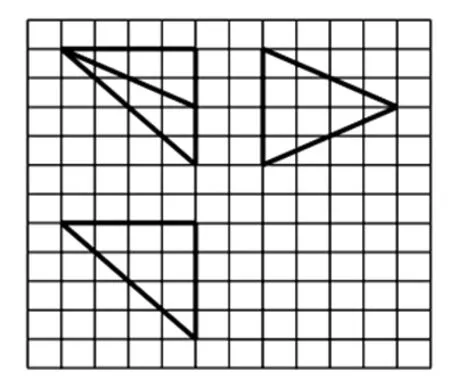
图1

例1 (2014年理科课标Ⅰ卷第12题)如图1，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( ).

分析：①三视图易确定此多面体为三棱锥，作出嵌入的载体——正方体；

②由正视图的中间实线AB入手(一般由三视图内的实线或虚线开始，由易到难，逐个确定各顶点)，由正视图可知点A应该是正方体中的点A′或A″，点B应该是正方体中的点B′或B″(图2)，但因为AB是实线，故A′与B′不能同时出现，由俯视图易知不能为A″，故能确定几何体的两个顶点为A′与B″(图3)；

图2 图3

③由俯视图的特征可知其上面的直角顶点C应为正方体中的C′或C″(图4)，由正视图可知点C′定存在，故确定几何体的第三个顶点为C′(图5)；

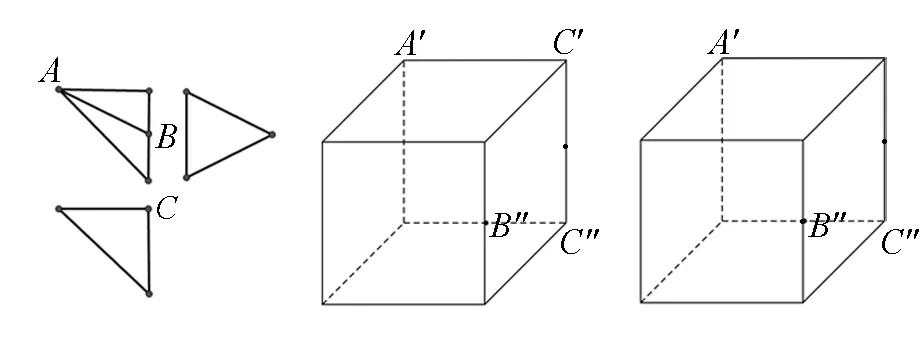
图4 图5

④由侧视图和正视图可知点D应为正方体中的C″，由正视图可知点C″定存在(图6)，故确定几何体的第四个顶点为C″.连接四个顶点为A′、B″、C′、C″就是所求的三棱锥(图7)；

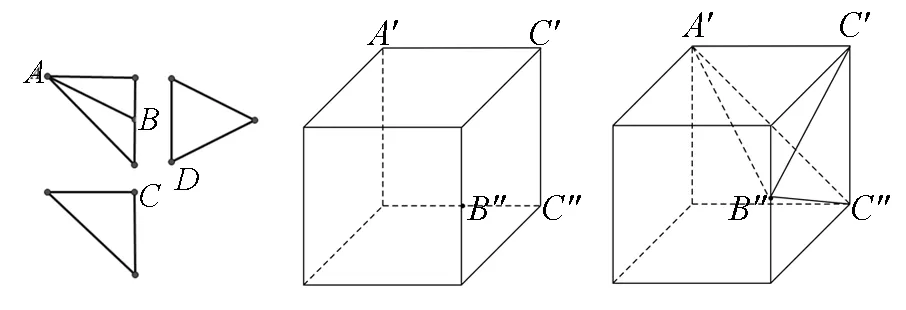
图6 图7

例2 某四面体的三视图如图8所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中最大的面积是( ).

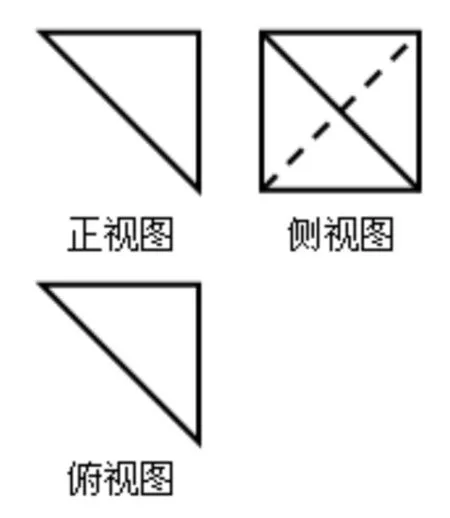
图8

分析：①从三视图易确定此多面体为三棱锥，作出嵌入的载体——正方体；

②由侧视图中间的虚线AB入手(“虚线”表示看不到的棱长，其在表面的可能性更大，而实线表示看得到的棱长，其位置在表面或中间都可以，故先虚线后实线更易解决问题.)由侧视图可知点A应该是正方体中的点A或A′，点B应该是正方体中的点B或B′(图9)，但因为AB是虚线，故A′与B′，A与B′不能同时出现，由正视图易知不能为A′，故能确定几何体的两个顶点为A与B(图10)；

图9 图10

③由侧视图中间的实线CD可知在几何体中应为C′D或C′D′(图11)，但由俯视图可得D′不存在，故确定几何体的另外两个顶点为C′，D(图12)；

图11 图12

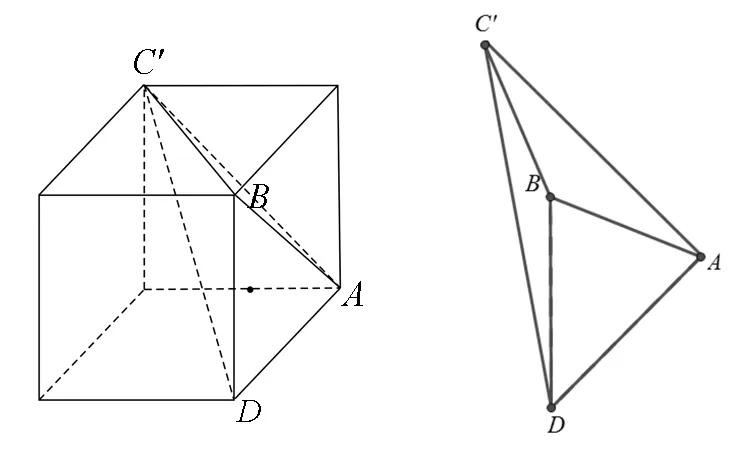
图13

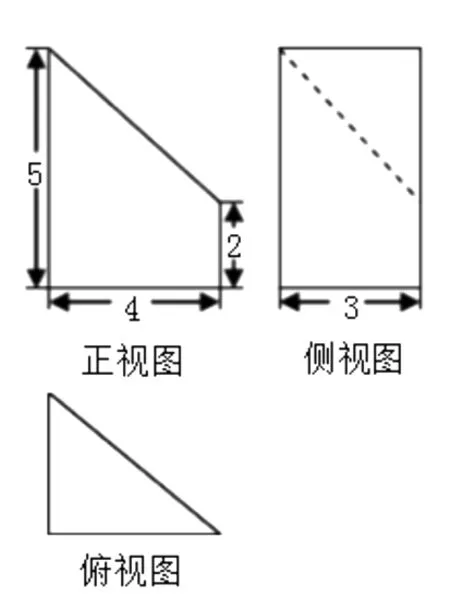
图14

例3 (2014年理科重庆第7题)某几何体的三视图如图14所示，则该几何体的表面积为( ).

A.54B.60

C.66D.72

分析：①由三视图易确定此多面体为三棱柱的一部分(由俯视图确定一个底面为直角三角形)，做出嵌入的载体——长方体的一半(图15)(长4宽3).

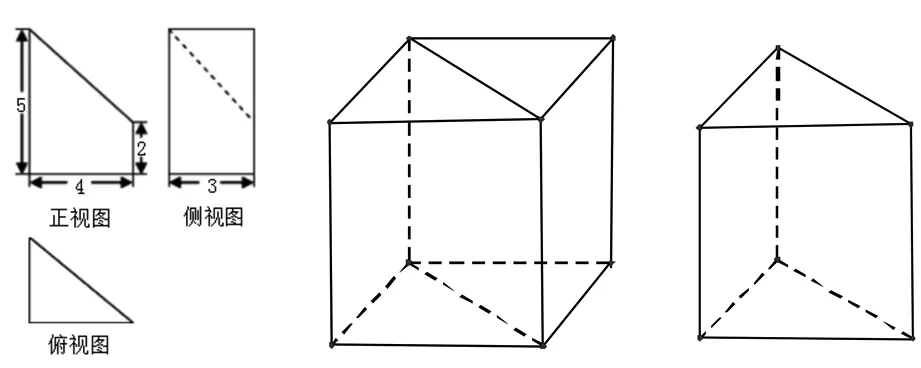
图15

②由侧视图的虚线(一般由三视图内的实线或虚线开始，由易到难，逐个确定各顶点)可知在侧棱AA′上存在一点D(AD=2)和点B′(图16)，由正视图可知存在点C′(图17)；

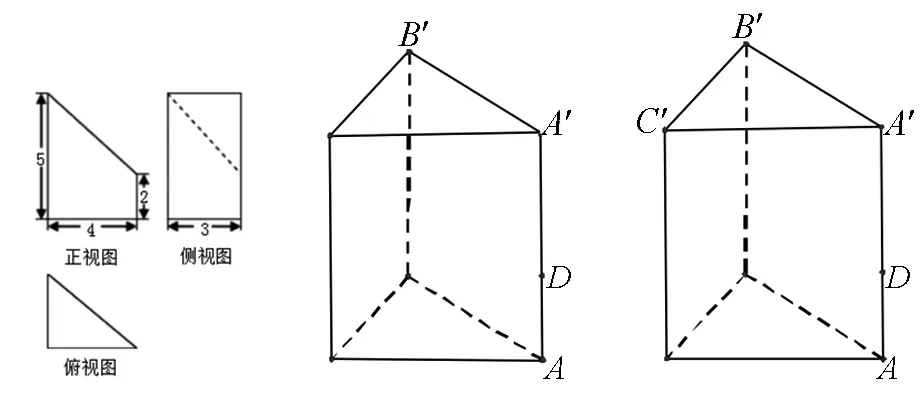
图16 图17

③由正视图和侧视图的下面可知底面的三个顶点A、B、C都存在(图18)，连接各顶点就是所求的几何体(图19)，将多余的线擦掉，从而得到其几何体，并求得表面积为60.

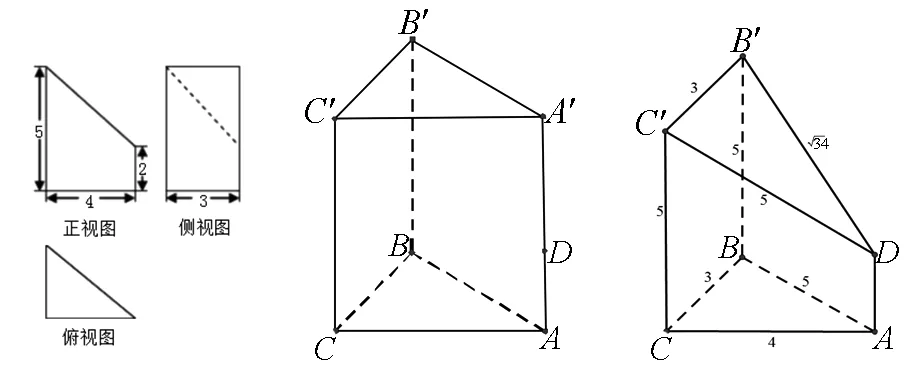
图18 图19

通过以上三道类似的例题，我们可以发现“嵌入法”就是将所求几何体嵌入到我们熟悉的几何体(一般为柱体)中，通过对其顶点的位置的确定后并连接各条棱线，然后再把多余的线擦掉，就能画出所要求的几何体.“嵌入法”这是一种解决三视图还原直观图问题的有效方法，其关键在于通过图形内的实线与虚线入手，结合三视图逐个判断顶点位置，特别是对较复杂的三视图问题，它能够有效的解决问题，体现了由易到难的解题思路，也是对“切割法”的另一种理解，是一种学生比较容易接受和实践的有效方法.

[1]王新宏.例析2014年高考三视图试题[J].数理化学习(高一二版)，2015(2):4-6.

[2]李红春，黄淑琴.先定线,再取点——一类由三视图还原直观图问题的简便解法[J].数学教学研究，2017，36(3):51-53.

[3]韩长峰.三视图还原出几何体的绝招[J].青苹果(高中版).2016(6):6-10.

[4]陈洙颖.以三视图还原几何体困难的原因及对策[J].中学生数理化(学研版).2017，(5)：60-61.

[5]刘玲珑.无规矩不成方圆——以三视图为例谈立体几何中的还原策略[J].中学数学，2016(21):72-73.

[6]吴学全.三视图高考常考题型及易错点解析[J].高中数理化,2015(23):22-23.