随机振动与冲击条件下电动车电池包结构响应分析∗

黄培鑫，兰凤崇，陈吉清

随机振动与冲击条件下电动车电池包结构响应分析∗

黄培鑫，兰凤崇，陈吉清

(1.华南理工大学机械与汽车工程学院，广州 510640； 2.广东省汽车工程重点试验室，广州 510640)

为提高电动汽车电池包结构安全性和电连接可靠性，更好地预判和分析电池包结构损伤和电接触可靠性，建立了电池包精细化模型，通过电池包模态试验验证了模型的有效性；从应力值和加速度两个方面分析了电池包在稳态随机振动和瞬态冲击下的结构损伤和电接触可靠性。结果表明，电池包整体模态对触点的动态响应影响很大；同一振动工况下不同位置触点的应力和加速度都很不均匀；冲击工况产生的交变应力比稳态工况对电池包造成的结构伤害和对内部电触点可靠性的影响都更大。分析结果可为电池包安全性设计、接触保护设计和疲劳寿命预测等提供参考。

车用电池包；随机振动；瞬态冲击；内部触点；动态响应

Keywords:EV battery pack； random vibration； transient impact； internal connection； dynamic response

前言

动力电池包作为电动汽车的储能部件，需要在变温、振动、冲击等条件下完成充放电功能。其结构设计应满足多变运行环境下和行驶工况下的机械承受、工作安全性和可靠性要求。其电连接应在振动冲击环境下保持良好接触，否则一方面由于接触不稳定引起接触电阻增大生热所损耗的能量可达到电池容量的20%[1]，另一方面电连接不可靠易引起短路、漏电，更严重的产生高温电弧熔化极柱并引燃周围材料，引发火灾[2]。了解电池包在振动、冲击环境下的结构损伤，掌握内部关键电接触点在车载振动环境下的响应对电池包结构设计与优化、电连接可靠性分析、接触保护设计和系统安全性评估等有重要意义。

典型的电池包开发流程是通过对试制样品进行振动、冲击试验来校核内外部结构的可靠性，再针对产品缺陷进行结构优化，研发成本高，开发周期长，试验过程还存在安全隐患。在设计开发阶段运用CAE技术进行虚拟工况分析，预测结构性能，结合评价体系进行结构优化和校验可大大降低研发成本，缩短开发周期，提高产品设计质量。

目前，电池包动态响应数值分析主要集中在箱体动强度设计[3-4]和疲劳寿命预测[5-6]两个方面，对内部结构振动状态的研究较少。本文中结合某电池包实例，建立了包含内部极片、触点等部件，考虑接触装配条件下的电池包动力学模型，并通过模态试验验证了模型的有效性；基于GB/T 31467.3—2015《电动汽车车用锂离子动力蓄电池包和系统第3部分:安全性要求与测试方法》中的振动测试要求，对电池包进行了稳态随机振动和瞬态冲击两个工况的仿真，从应力值角度分析了振动引起的结构损伤，从加速度角度描述了内部电接触点所处的振动环境。分析结果可为电池包安全设计提供参考。

1 分析方法

1.1 分析流程

采用有限元通用软件对电池包动态响应进行数值分析，分析流程如图1所示。首先根据电池包几何模型进行模型离散化处理，分析离散化后模型的网格独立性，综合考虑计算精度和计算成本确定网格类型和数量；然后基于实际的装配关系，确定各组件间的接触参数，加载实测得到螺栓预紧力，求解装配后预应力场；进行电池包自由模态仿真并与试验结果对比，验证模型的有效性；最后进行约束模态求解，采用振型叠加法计算随机稳态和冲击瞬态工况下电池包的振动响应，对内外部结构的响应值、响应分布进行分析。

1.2 数值方法

1.2.1 电池包随机响应求解

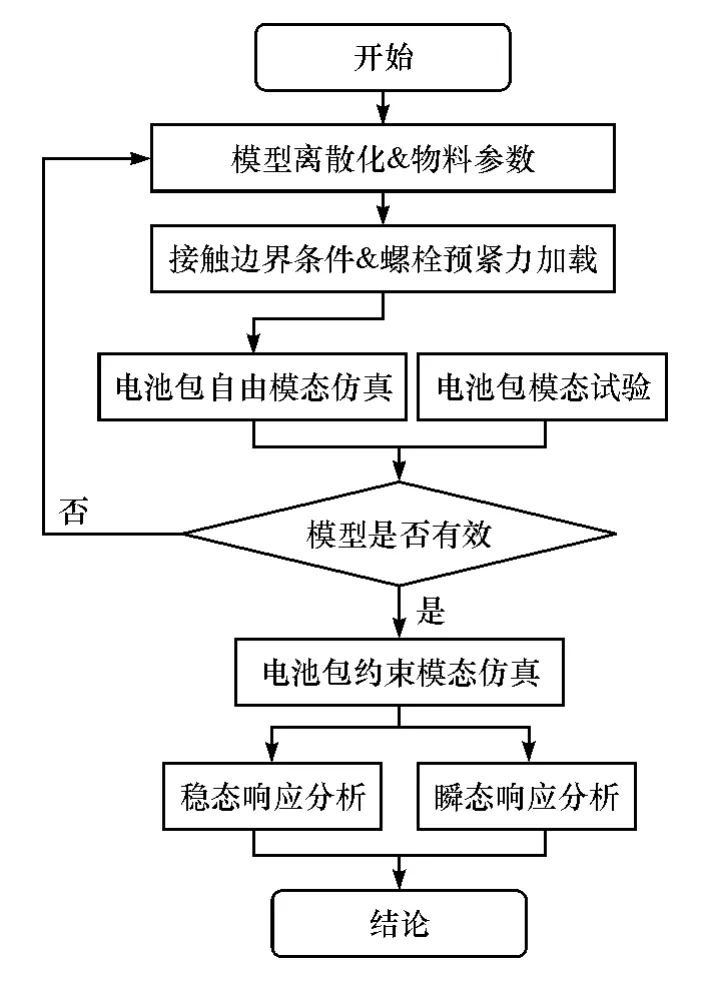
图1 分析流程

随机振动是指未来任一给定时刻的瞬时值不能预先确定的机械振动，无法用确定性函数而须用概率统计方法定量描述其运动规律的振动，其响应(位移、速度、加速度)由以下方法获得[7]。

n自由度系统随机振动动力学方程为

式中:M，C和K分别为系统的质量阵、阻尼阵和刚度阵；X，和分别为节点的位移、速度和加速度矢量；f(t)为系统激励。当激励为加速度(t)，且功率谱密度为S(ω)时，运动方程可表示为

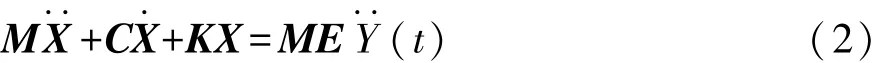
式中:E为加速度向量。首先对系统进行模态求解，令C＝0，f(t)＝0，得到系统的自由振动方程和特征方程为

取系统的前 n阶固有频率 ωi和振型 xi，i＝1，…，n。 由于主质量 Mp＝xTMx，主刚度 Kp＝xTKx，且有ω2i＝kpi/mpi，故可将振型乘以一个常数乘子得到正则化振型φi，则经典阻尼下，引入模态坐标ui，式(2)可离散为

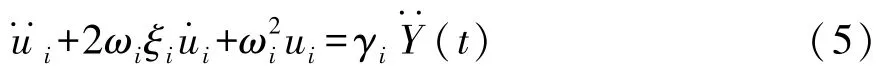
式中:ξi为系统第i阶阻尼比；γi为第i阶振型参与系数

X(t)与ui的关系为

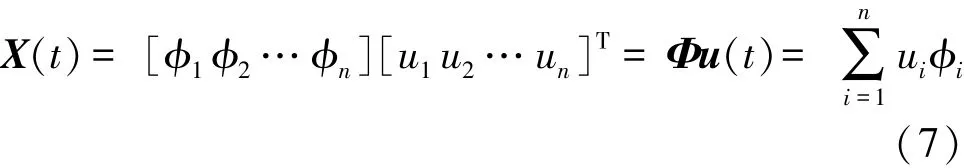
式(5)在时间域内的解为

式中hi(τ)为系统的第i阶脉冲响应函数。将式(8)带入式(7)可得

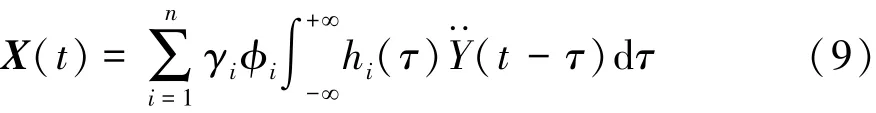
则X(t)的自相关函数为

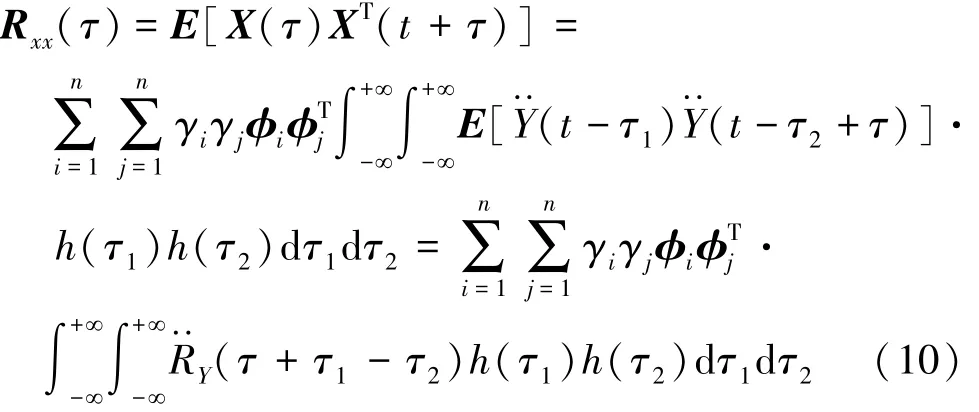
根据维纳-辛钦关系，输出功率谱密度函数是输出自相关函数的傅立叶变换，通过交换积分次序并引入变量代换θ＝t+τ1-τ2，可得输出功率谱密度函数为

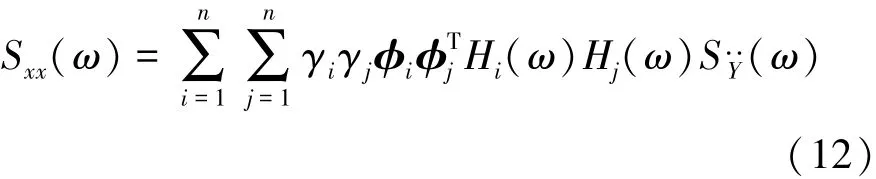
式(12)计算量很大，工程上一般使用简化近似方法，即将式中的交叉项忽略掉，响应功率谱密度简化为

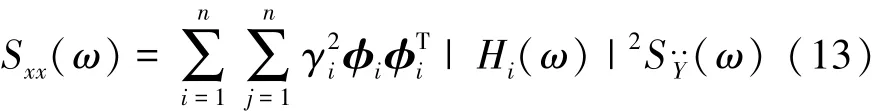
响应均方值为

汽车所受到的随机振动大部分满足零均值的高斯分布，其响应量(位移、速度、加速度)也满足该分布，由于分布均值为零，响应均方值σ2x即为分布的方差，求得其标准差σx即获得响应值的概率分布。

1.2.2 电池包应力分析

与求解振动响应量类似，对于随机振动下的应力分析，工程界常用的是文献[8]中提出的动应力分布的三区间法，即任意一点动应力瞬时值满足零均值的高斯分布。文献[8]中将Von Mises应力处理成3个区间，在应力区间 σF～σF，-2σF～2σF和-3σF～3σF发生振动的时间分别为总时间的68.3%，95.4%和99.73%。仿真求解得到的RMISES即为米赛斯应力分布标准差σF。

1.3 电池包模态试验

为验证整体动力学模型的有效性、获得各阶主模态的阻尼比参数，采用单点激振多点拾振的方法对电池包进行模态试验。悬挂前确认所有螺钉按标准紧固，各个部件接触面紧密贴合，若存在间隙会大大增加系统的非线性度，影响测试结果精度。同时把易受激振动的附件如信号线、正负极立柱等部件固定好，避免部件因自由振动影响试验，对传感器作绝缘处理。电池包整体参数如表1所示，共设置116个测点，频率分辨率为 1Hz，测量频率范围 0～200Hz。试验过程如图2所示。

表1 电池包整体参数

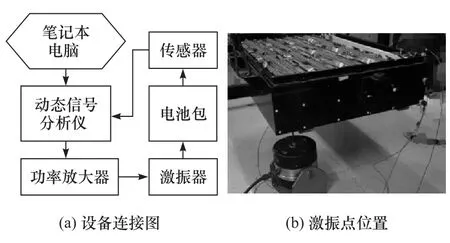
图2 电池包模态试验

2 数值模型的建立

一例实际电池包示意图如图3所示，由电池、壳体、压杆、压盖、内架和绝缘板等部件组成；控制电源、排气扇等电气附件简化处理，通过质量单元平均分配到相应安装点上。各部件的材料参数和单元类型如表2所示，模型共包括349 164个单元，其中实体单元117 113个，节点266 441个，最小单元尺寸为1mm，最小雅克比为0.5，满足计算要求。单体电池之间通过极柱与大极片激光点焊组成模组(见图4)。

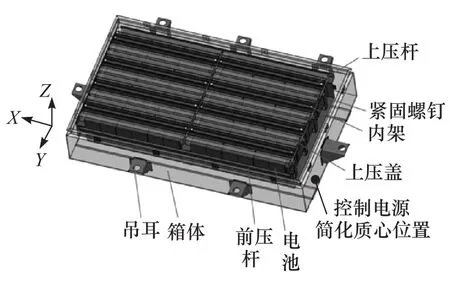
图3 电池包示意图

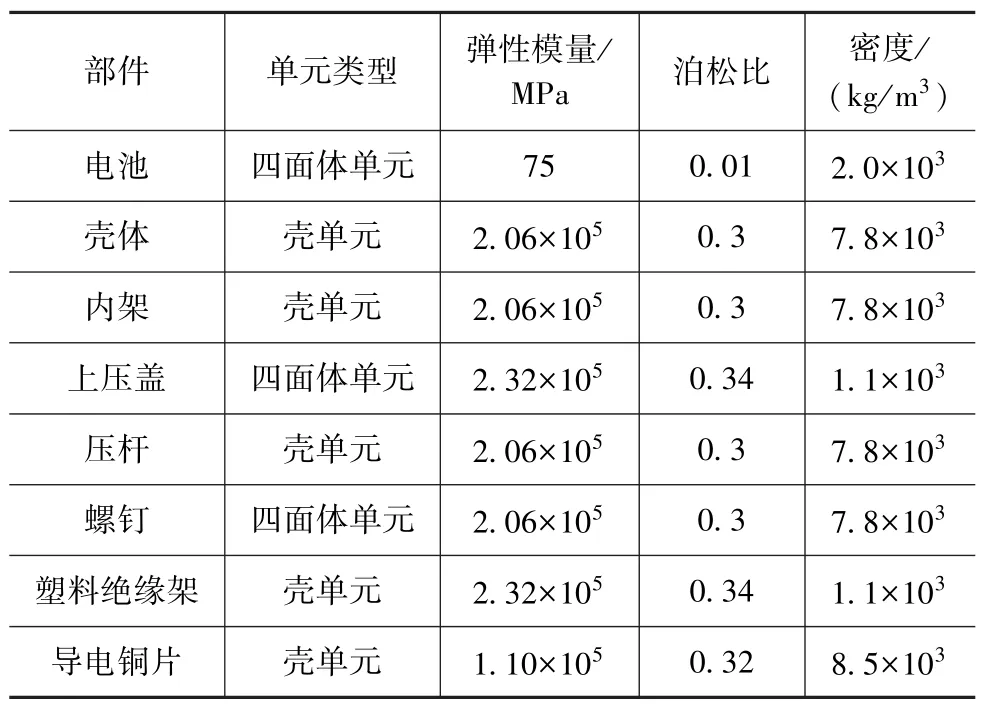
表2 电池包各部件材料参数

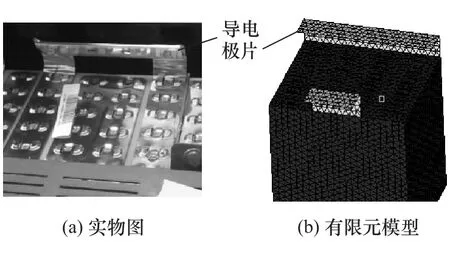
图4 模组之间的导电极片

紧固螺钉模组之间的电连接如图5所示，一组紧固螺钉将两个模组的导电极片和电压反馈信号线固定在压盖上，模型中用刚性单元模拟模组极片的螺栓连接。沿螺钉轴向的振动冲击会引起其与压盖间的轴向位移，使极片间的接触面积进而使得接触电阻皆随振动发生周期性变化。长时间的振动环境下，螺钉的紧固能力衰减，导电极片间的接触电阻上升，当接触电阻的量级与电池欧姆内阻量级相当时，会引起电压反馈故障[9-11]。

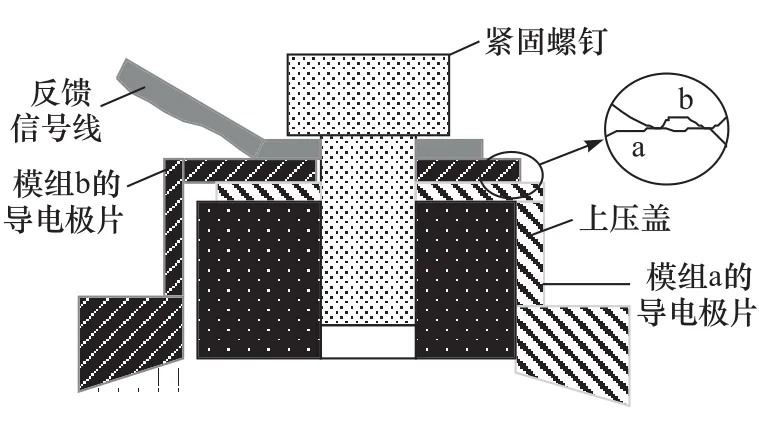
图5 模组之间的电接触示意图

2.1 模型的验证

将实测得到的预紧力矩转化为预紧力施加在实体螺栓上，定义各个接触面的接触参数，求得接触条件下的电池包自由模态仿真与试验结果，如表3所示，固有频率的误差在3.3%以内且振型一致，验证了模型的有效性。约束电池包7个吊耳中心位置，求解约束模态前4阶结果如图6所示，1阶振型为底板1阶弯曲引起的中前部Z向振动，2阶振型为底板2阶弯曲，3阶振型为电池组上下振动引起的整体模态，4阶振型为电池组饶Z轴扭动引起的整体模态。

表3 电池包自由模态仿真与试验结果

图6 电池包约束模态

2.2 激励谱的选取

参考GB/T 31467.3—2015《电动汽车车用锂离子动力蓄电池包和系统第3部分:安全性要求与测试方法》中的振动试验要求，对安装在车辆乘员舱下部的电池包分别施加X，Y和Z轴稳态随机激励，其PSD值如表4所示，RMS为加速度的均方根值。冲击工况为Z轴施加25g和15ms的半正弦波，求解时长设置为0.1s，前15ms施加冲击激励，后85ms观察激励去除后的自由振动。

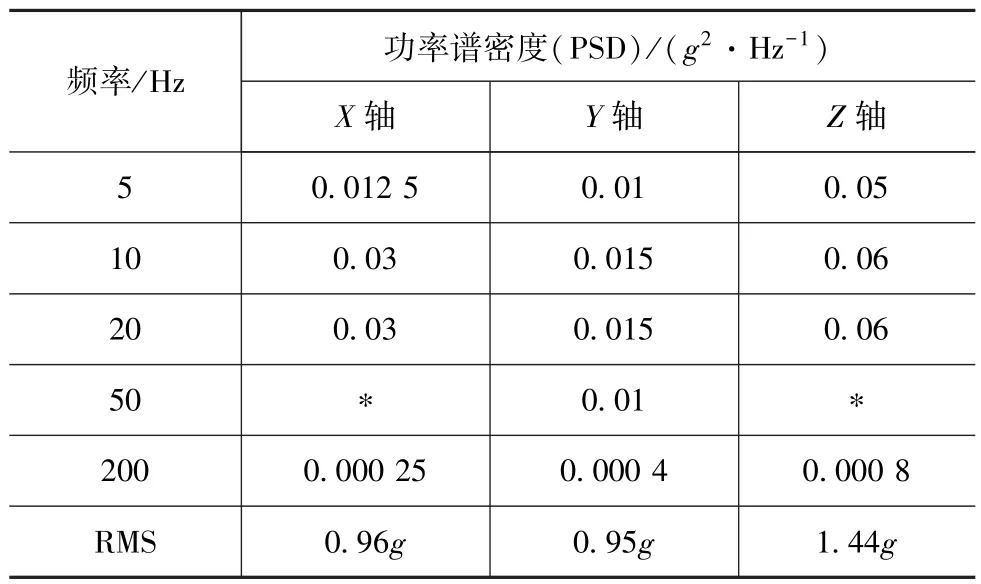
表4 加载激励PSD值

3 结果分析

振动、冲击环境会造成电池包结构损伤，影响内部电接触稳定性。下面从应力的角度分析振动、冲击条件下的结构损伤，从加速度的角度描述内部触点振动环境，为电池包结构疲劳耐久性分析、安全性设计和内部电接触可靠性分析提供参考。32个带反馈信号线的关键电接触点位置如图7所示。

图7 32个关键触点位置

3.1 应力分析

3.1.1 稳态工况

对于箱体结构(见图8)，应力较大位置多数出现在电池包前端，通常为总正负极柱，保护电路等电气构件位置。X，Y和Z轴激励下最大动应力RMISES分别出现在右内架和壳体的前端焊点、左内架和壳体的前端焊点，对应的3σF分别为82.8，258.9和359.1MPa。Z轴激励下的动应力3σF值略高于内架材料Q345的屈服强度345MPa，但动应力瞬时值超越345MPa属小概率事件，可认为结构满足稳态激励下的安全性要求。对于该款电池包可考虑对前端电气构件进行刚度补强，改善内架与壳体的焊接工艺，避免应力集中现象，增长焊点的疲劳寿命。

对于电池模组结构(见图9)，在沿X，Y，Z轴的激励下最大动应力RMISES分别为20号触点区域的3.2MPa，10号触点区域的10.7MPa和32号触点区域的62.3MPa；即对应的3σF分别为9.4，32.1和186.9MPa。以Z轴激励下的最大响应为例，32号触点应力瞬时值在99.7%振动时间内小于186.9MPa。

3.1.2 冲击工况

由于冲击激励是半正弦波形，电池包的响应也呈周期性变化，以一个周期的位移响应为例(见图10)，振动形态为中前部上下反复振动，与1阶约束模态振型相接近。冲击过程中电池包壳体最大应力231MPa出现在14ms，位置同Z轴稳态激励下的最大动应力点。

图9 电池模组RMISES云图

图10 冲击工况下电池包位移时域变化

对于电池模组(见图11)，所有触点应力是交变的，衰减趋势基本一致，在14ms附近达到第一个峰值，激励解除后电池包在阻尼的作用下以近似40.5Hz的频率进行自由衰减振动，这是由于电池包Z向振动主要由1阶约束模态主导。在整个时域范围内，大部分触点的应力值都比稳态工况时高，最大应力值出现在20号触点位置，达到了140.4MPa，如图12所示。半正弦波冲击工况中引起的交变应力环境比稳态工况更恶劣，造成的结构损伤更大，对电连接结构的材料强度和疲劳耐久性等要求更高。

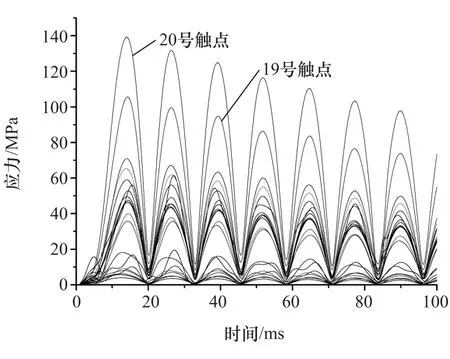
图11 各触点应力的时域变化

图12 14ms时各触点应力云图

3.2 加速度分析

3.2.1 稳态工况

电池模组在沿X，Y，Z轴的激励下最大加速度响应触点号分别为17，12，12(见表5)。同一方向激励下不同位置触点的加速度响应差异很大，呈现很强的不均匀性，以Z轴激励为例，最大响应为12号触点的18.9g，最小响应为22号触点的1.8g。3个工况激励RMS排序为:Z轴＞X轴＞Y轴，触点响应差异程度排序为:Z轴＞X轴＞Y轴，表明各触点振动响应的不一致性随着振动工况的恶化而增大。长时间振动环境不一致会使得各触点的接触稳定性和连接疲劳寿命也呈现不一致，振动恶劣的位置将率先出现疲劳破坏。

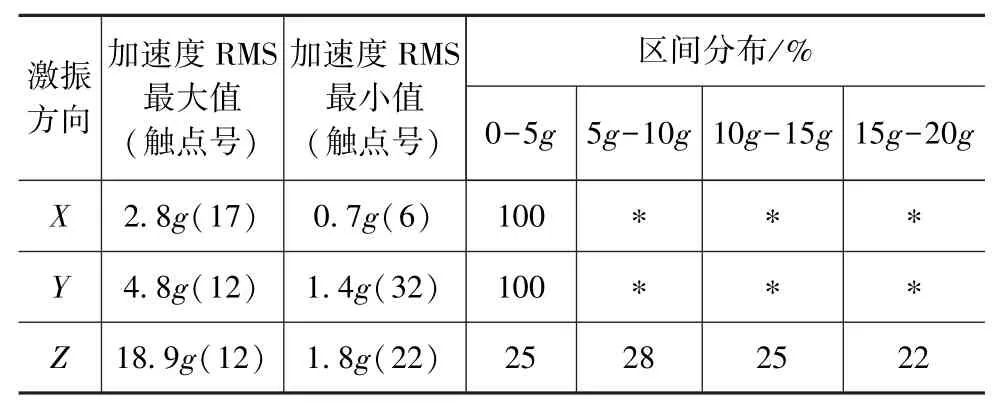
表5 触点稳态响应统计表

由图13可见，X和Y轴激励下所有触点的RMS集中在0～5g。Z轴激励下的加速度RMS在4个区间内的分布分别为25%，28%，25%和22%。Z向工况较X和Y向更恶劣，这是因为电池包1阶约束模态振型以Z向运动为主。

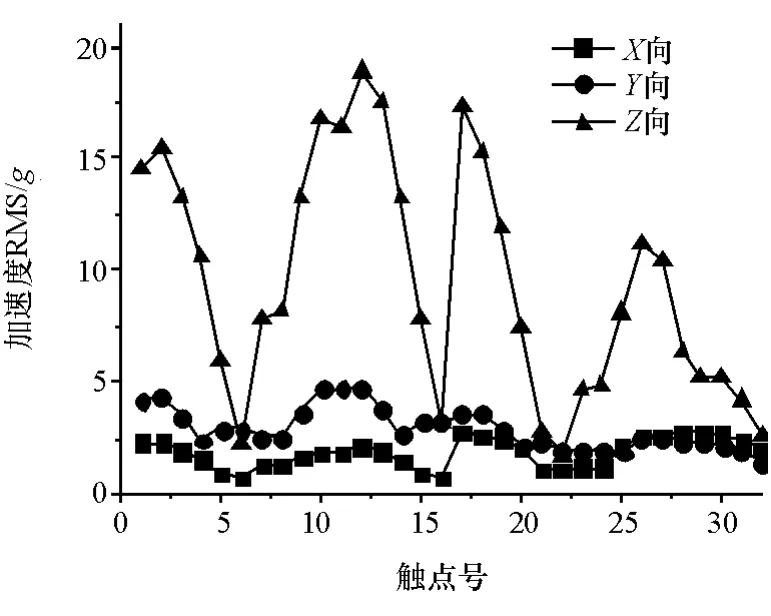
图13 触点位置的RMS

图14 为3个工况下最大响应点的加速度功率谱密度曲线，Z轴激励下响应在39.45Hz附近振动被放大，对应电池包1阶约束模态频率。Y和X轴激励下最大共振峰出现在81和118Hz附近，对应的振型为电池组Y和X向运动引起的电池包整体模态，可见电池组整体运动对触点的动态响应影响很大。

图14 稳态工况触点加速度频域分布

3.2.2 冲击工况

电池模组Z向冲击与Z向稳态振动下的加速度响应分布相似，响应较大的触点号同为12，13和17，但响应值比稳态下大很多，且呈交变周期变化(见图15)。最大加速度响应61.1g出现在12号触点位置，在100ms时仍达到32.9g，说明该电池包对振动的衰减能力较差。综合稳态工况和冲击工况，从连接可靠性角度较危险的触点位置是12和17。

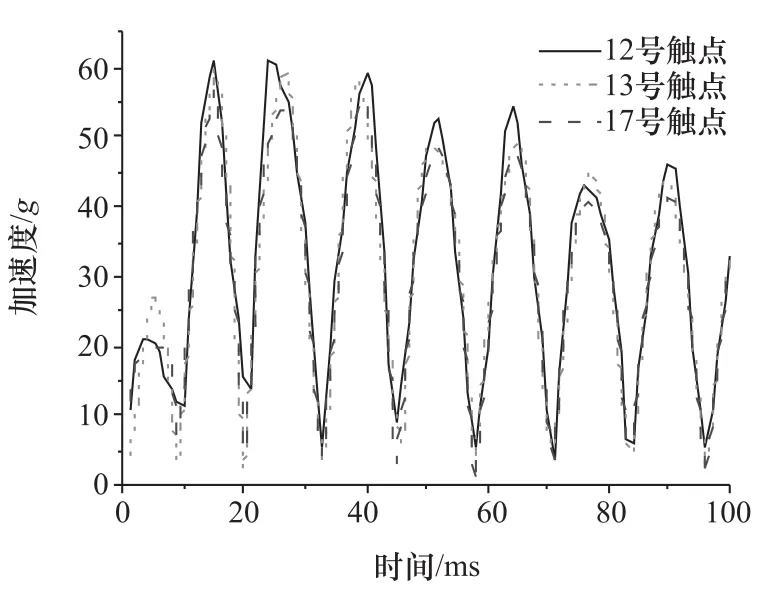
图15 12，13和17号触点加速度时域变化

4 结论

(1)电池包的安全性和可靠性严重制约着电动汽车的发展，其开发环节亟待进行内外部复杂结构的可靠性分析和优化，消除在设计阶段存在的各种安全隐患。本文中通过建立电池包精细化模型，获得箱体和内部触点在稳态随机激励和瞬态冲击条件下应力和加速度的分布，可为电池包安全性设计、接触保护设计和疲劳寿命预测等提供设计保障。建议整车厂和电池包开发企业继续加大对实车复杂环境下的电池包系统安全和可靠性研究的关注和开发投入。

(2)通过对实例电池包的研究，发现同一振动工况下，不同位置触点的应力和加速度差别很大，以Z轴激励为例最大加速度响应为12号触点的18.9g，最小响应为22号触点的1.8g。长时间的振动环境不一致会导致各触点的结构损伤、连接可靠性也呈现不一致，导致各电接触位置的接触电阻分化严重，影响整个电池包的电压一致性。

(3)电池包整体模态对关键触点的动态响应影响很大，加速度响应在低阶模态频率处被放大。电池成组时尽量避免振型较大的位置，或对处于该位置的电接触连接进行针对性设计；电池包结构设计应考虑隔振、减振，对变形较大位置进行刚度补强或增加阻尼。

(4)冲击工况下电池包箱体最大应力为231MPa，触点处最大应力为140MPa。电池包结构设计不仅要考虑路面不平度稳态激励下的结构可靠性，更要考虑瞬时大冲击等极端行驶条件下的结构安全性。

[1] TAHERI P，HSIEH S，BAHRAMI M.Investigating electrical contact resistance losses in lithium-ion battery assemblies for hybrid and electric vehicles[J].Journal of Power Sources，2011.196(15):6525-6533.

[2] YAOLei， WANG Zhenpo， MA Jun.Fault detection of the connection of lithium-ion power batteries based on entropy for electric vehecles[J].Journal of Power Sources，2015(293):548-561.

[3] 孙小卯.某型电动汽车电池包结构分析及改进设计[D].长沙:湖南大学，2013.

[4] 董相龙，张维强.电动汽车电池箱结构强度的有限元分析及其改进设计[J].机械强度，2015，37(2):312-316.

[5] 吴长德，戴江梁，唐炜，等.基于某电动汽车电池箱焊点的疲劳寿命预测与优化[J].机械强度，2013，35(5):663-667.

[6] 王文伟，程雨婷，姜卫远，等.电动汽车电池箱结构随机振动疲劳分析[J].汽车工程学报，2016，6(1):10-14.

[7] 吕奇峰，张卫红，张桥，等.随机振动响应下的组件结构布局优化设计[J].航空学报，2010(9):1769-1775.

[8] 庄表中，陈乃立.随机振动的理论及实例分析[M].北京:地震出版社，1985:216-222.

[9] 支宏旭.综合环境应力下航空电连接器电接触特性的试验研究[D].哈尔滨:哈尔滨工业大学，2015.

[10] 郑岳久.车用锂离子动力电池组的一致性研究[D].北京:清华大学，2014.

[11] OFFER G J，YUFIT V，HOWEY D A，et al.Module design and fault diagnosis in electric vehicle batteries[J].Journal of Power Sources，2012，206:383-392.

The Structural Response Analysis of EV Battery Pack Under Random Vibration and Impact Conditions

Huang Peixin，Lan Fengchong＆ Chen Jiqing
1.School of Mechanical＆ Automotive Engineering， South China University of Technology， Guangzhou 510640；2.Guangdong Provincial Key Laboratory of Automotive，Guangzhou 510640

To enhance the structural safety and electric connection reliability of battery pack in electric vehicle and to better predict and analyze the structural damage and connection reliability of battery pack，a refined model for battery pack is established with its effectiveness verified by modal test，and the structural damage and connection reliability of battery pack under steady random vibration and transient impact are analyzed from the aspects of stress and acceleration.The results show that the overall modality of battery pack has a significant influence on dynamic response of electric connections and under a same vibration excitation，the stresses and accelerations of connections in different positions are significantly different.Compared with steady random vibration conditions，the alternating stresses produced in transient impact conditions have greater effects on the structural damage and internal connection reliability of battery pack.The results of analysis provide a reference for the safety design，connection protection design and fatigue life prediction of battery pack.

10.19562/j.chinasae.qcgc.2017.09.017

∗广东省科技计划项目(2014B010106002，2015B010137002和2016A050503021)资助。

原稿收到日期为2016年8月5日。

陈吉清，教授，E-mail:chjq＠scut.edu.cn。