基于模型融合与自适应无迹卡尔曼滤波算法的锂离子电池SOC估计∗

刘伟龙，王丽芳，廖承林，王立业

基于模型融合与自适应无迹卡尔曼滤波算法的锂离子电池SOC估计∗

刘伟龙1，2，王丽芳1，廖承林1，王立业1

(1.中国科学院电力电子与电力传动重点实验室电工研究所，北京 100190； 2.中国科学院大学，北京 100049)

为提高电动汽车动力电池SOC的估计精度，本文中对锂离子电池模型与参数辨识算法、自适应无迹卡尔曼滤波(AUKF)算法和基于电池模型融合的SOC估计算法进行研究。建立了具有明确物理意义的电池电路模型，采用基于遗传算法(GA)的模型参数辨识算法，设计了基于AUKF的电池SOC估计方法，并基于贝叶斯信息准则，提出了电池模型融合方法，实现了基于模型融合与AUKF的电池SOC估计。仿真结果验证了该方法具有较高的精度。

锂离子电池；SOC估计；参数辨识；自适应无迹卡尔曼滤波；模型融合

Keywords:Lithium-ion battery；SOC estimation；parameter identification；AUKF；model fusion

前言

目前，电动汽车代表汽车产业的发展方向已经成为普遍共识[1]。动力电池作为电动汽车的主要能量来源，决定着电动汽车的续航里程、动力性能和使用经济性。锂离子电池由于具有能量密度大、电压平台高、循环寿命长和无记忆效应的优点，成为电动汽车动力电池的主流选择。为保障动力电池安全、高效、稳定的运行，须使用电池管理系统进行监测管理。而SOC作为动力电池的主要内部参数和电池管理系统的重要监测参数，影响到电动汽车系统能量流控制策略，以及驾驶员的车辆使用决策。对其进行实时精确的估计具有重要意义。

动力电池SOC估计方法主要可以分为:安时积分法[2]、开路电压法[3]和高级估计方法[4-6]。其中，安时积分法作为经典SOC估计方法广泛应用于电池管理系统中，其通过对监测电流进行积分运算得到充放电量，获取电池SOC，具有累计误差的缺陷；开路电压法利用电池开路电压与SOC呈现的单调关系，使用插值原理得到电池SOC，因此是一种电池静置态估计SOC方法，在电动汽车运行过程中，无法估计电池SOC；高级估计方法主要包括神经网络、支持向量机和卡尔曼滤波等，其中，卡尔曼滤波作为最小方差意义上的最优估计方法，具有收敛快、对SOC初值不敏感的优点而得到广泛研究，但其也具有对电池模型精度要求高的缺点。

动力电池模型的研究主要可以分为3类:电化学机理模型[7-8]、经验模型[9-10]和等效电路模型[11-12]。其中，电化学机理模型通过电化学反应第一性原理，建立电池的偏微分方程模型，该模型含有大量电化学参数，计算复杂，并且不具备通用性。经验模型是基于实验数据通过输入输出量的非线性关系来表征其外部特性，该模型依赖实验数据，很难满足预测精度要求。等效电路模型是将电池等效为集总参数电路，该模型具有便于分析应用，通用性好的优点，取得了广泛应用。

基于上述研究，本文中提出基于等效电路模型的AUKF算法估计电池SOC，针对电池模型要求高精度问题，采用模型融合技术提高电池模型精度。

1 锂离子电池模型与参数辨识算法

1.1 锂离子电池模型

建立电池模型是进行电池SOC估计的基础[13-15]。典型的电池电路模型有Rint模型、Thevenin模型和DP模型等。本文中基于电极阻抗谱电路模型，建立的电池电路模型如图1所示。其中，Uoc为电池的开路电压；Rs为电池的等效内阻，与电池的欧姆极化对应；Cdl为双电层电容，与电池的浓差极化对应；ZF为电化学阻抗，与电池的电化学极化对应；Rt为电荷转移电阻；n-RC环节对应于电化学极化的迟滞效应；n(n＝0，1，2，…)为模型阶次；Ut为动力电池的端电压；iL为动力电池的电流，图示充电方向为正，反向放电方向为负。

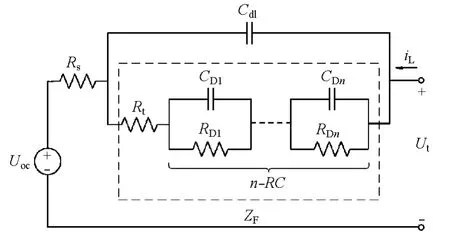
图1 锂离子电池等效电路模型结构

由图1可知，当n＝0时，电池模型转化为经典的Thevenin模型，n越大，电池模型的精度越高，但运算越复杂，本文中仅对n＝0，1，2进行分析。

n＝0时，电池模型系统方程为

n＝1时，电池模型系统方程为

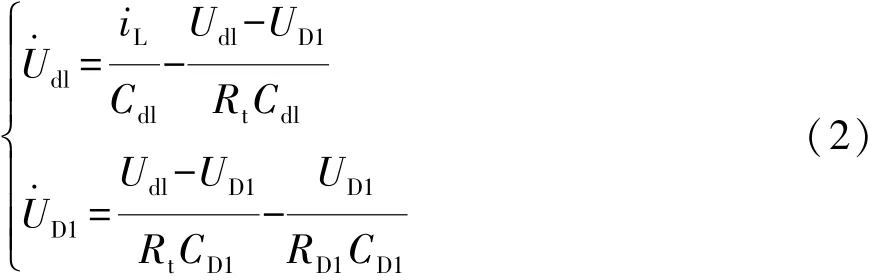
n＝2时，电池模型系统方程为

n＝0，1，2 时，电池模型检测方程为

1.2 模型参数辨识算法

本文中采用GA辨识模型参数，GA是一种启发式搜索算法[16]，以编码空间代替参数空间，适应度函数作为评价依据，对随机初始化种群作用选择函数与遗传机制，实现种群进化，最终得到合格个体，及问题相对最优解。本文中选取电池模型端电压估计值均方差的倒数作为适应度函数:

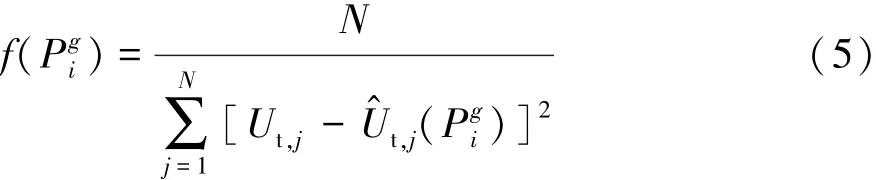
式中:P为遗传种群；g为进化次数；i为种群个体；N为适应度函数应用监测数据数；U＾t为端电压估计值。

2 AUKF估计算法

UKF是针对非线性系统的状态估计方法，使用无迹变换实现状态均值与协方差的传播。离散时间非线性系统可表示为

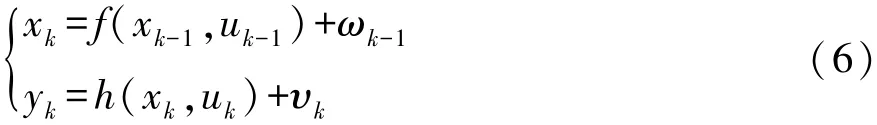
式中:x为系统状态；k为监测数据序号，k＝1，2，…；u为系统输入；y为系统检测值，ω～(0，Q)为系统白噪声；υ～(0，R)为监测白噪声。

2.1 电池模型离散时间方程

基于模型的AUKF估计算法[17]需将式(1)～式(3)电池模型系统方程离散化。本文中以n＝1为例，说明电池模型系统方程的离散化处理过程。

将电池SOC作为电池模型的附加状态，由安时积分法得到电池SOC的离散时间表达式为

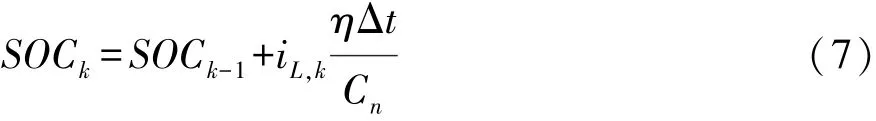
式中:η为电池库伦效率；Δt为系统的采样时间；Cn为电池容量。

将式(2)在频域内改写，并利用双线性变换法从s平面映射到Z平面，映射公式为

进行Z逆变换，而后与式(7)合并，结合电池模型检测方程，可得电池模型离散时间方程:

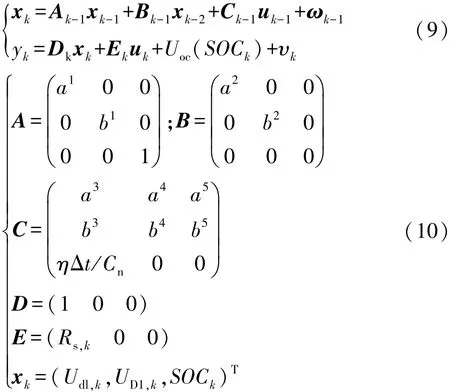
式中ai和bi为电池模型参数组成的有理式，i＝1，2，…，5。

2.2 AUKF算法流程

基于式(9)电池模型离散时间方程，展开AUKF算法，算法流程如下。

(1)AUKF算法初始化

右上标“-”表示先验估计，“+”表示后验估计。k＝0 时，设置初始状态 x＾+0，初始状态后验误差协方差P+0，初始系统噪声协方差矩阵Q0，初始检测噪声

协方差矩阵R1，噪声协方差匹配窗口长度L:

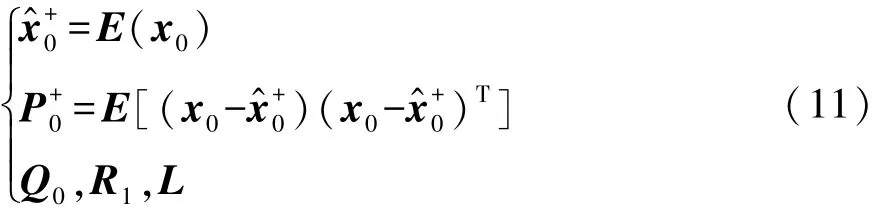
(2)先验估计，实现(k-1)+到k-的更新

a.选择sigma点

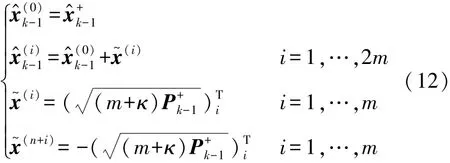
本文中采用sigma点对称采样策略，对应加权系数为

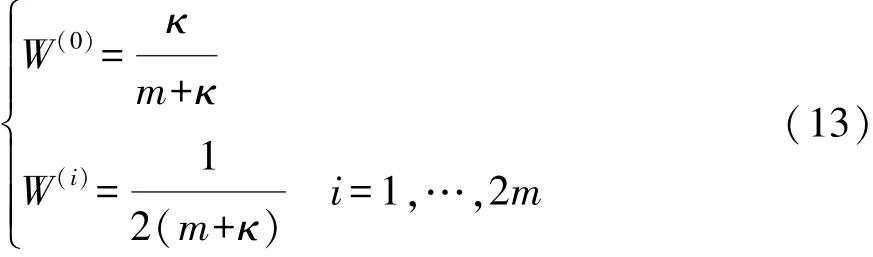
b.电池模型状态估计x＾更新

电池模型状态先验估计:

电池模型状态先验估计误差协方差:

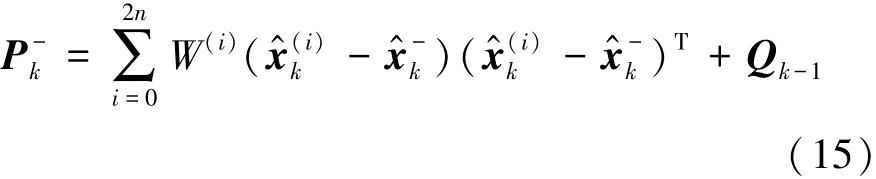
c.sigma点再选择

对电池模型状态先验估计值再次选择sigma点如下:

对应加权系数同式(13)。

d.电池模型输出估计

得到电池模型输出估计与输出协方差估计如下:

计算电池模型先验估计x＾-k与输出估计 y＾k的协方差:

(3)后验估计，实现时间k-到k+的推导

基于卡尔曼滤波原理，电池模型状态与协方差后验估计为

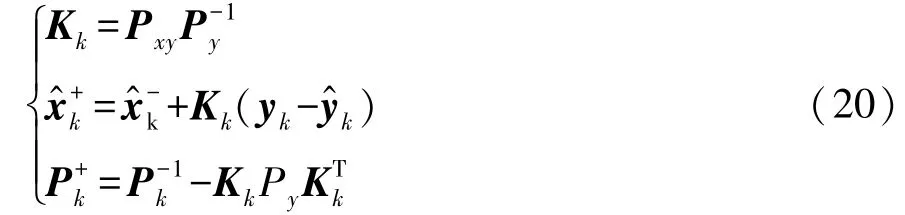
自适应协方差匹配:

(4)时间更新

将电池模型状态与协方差k+后验估计变换为第k次监测数据初值，进行时间k+到(k+1)-电池模型状态先验估计。

3 基于模型融合的SOC估计算法

电池模型精度与电池模型阶次呈一定正相关关系，而电池模型阶次的提高，会占用更多的计算资源，影响算法实时性，如何在电池模型阶次、电池模型精度与算法实时性之间进行平衡选择具有重要意义。本文中基于贝叶斯信息准则(BIC)构建电池模型不同阶次融合方法，并提出基于模型融合的SOC估计算法。

模型融合广泛应用于目标跟踪、模式识别等领域，可以解决基于单一模型的算法失效问题。BIC是考评综合最优配置的指标，本文中采用其作为不同阶(n＝0，1，2)电池模型融合标准，其表达式如下:

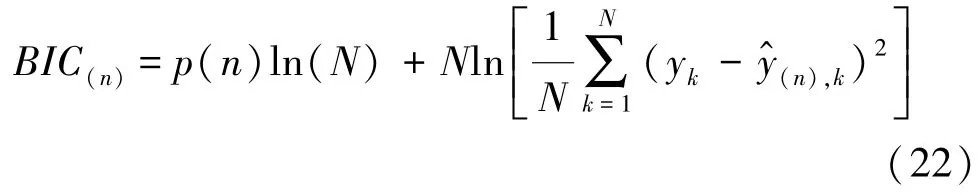
式中:BIC(n)为 n 阶电池模型 BIC 考评值，n＝0，1，2；N为BIC考评数据长度；p为电池模型参数个数，是模型阶次的函数；y＾(n)为n阶电池模型输出估计。式右边第1项表示模型阶次对计算复杂度的影响，ln(N)为惩罚系数，引入了样本容量的影响。式(22)右边第2项表示模型的预测精度。BIC越小，电池模型越优。如果BIC(n)＞BIC(n+1)，则增加模型阶次，反之，将保持模型阶次。由图1所示电池模型结果可知，模型阶次增加1个，模型参数增加2个。由式(22)可知，模型阶次增加的条件可表示为

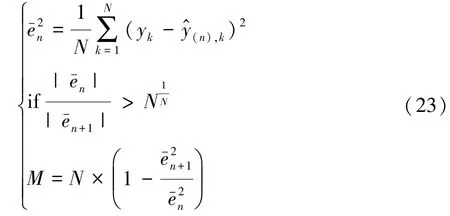
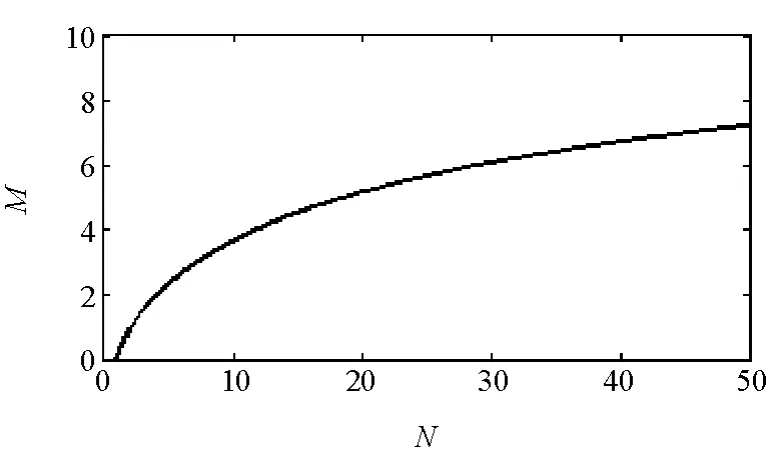
图2 考评数据长度与累计估计误差平方和

由图2可见，N越大，M就越大，即BIC越倾向于对电池模型的长期考评，体现电池模型的长期优势；反之，BIC越倾向于对电池模型的短期考评，体现电池模型的短期优势。本文中N取10，当N＝10时，即｜｜/｜｜＞0.7943(M＝3.6904)时，增加模型阶次，此时，BIC值能较好地兼顾电池模型的长期与短期优势。基于BIC的模型融合方法可以表述为

式中:w(i)为i阶模型选择权重。

本文中对于每个阶次的电池模型均应用AUKF算法进行SOC估计，分别以SOC＾(0)，SOC＾(1)和SOC＾(2)表示，针对不同阶次电池模型输出估计 y＾(0)，y＾(1)和y＾(2)分别进行BIC考评，应用模型融合方法，得到对应每个阶次电池模型的选择权重w(0)，w(1)和w(2)，进而得到基于模型融合的SOC估计为

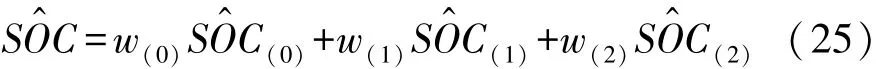
基于模型融合的SOC估计算法如图3所示。

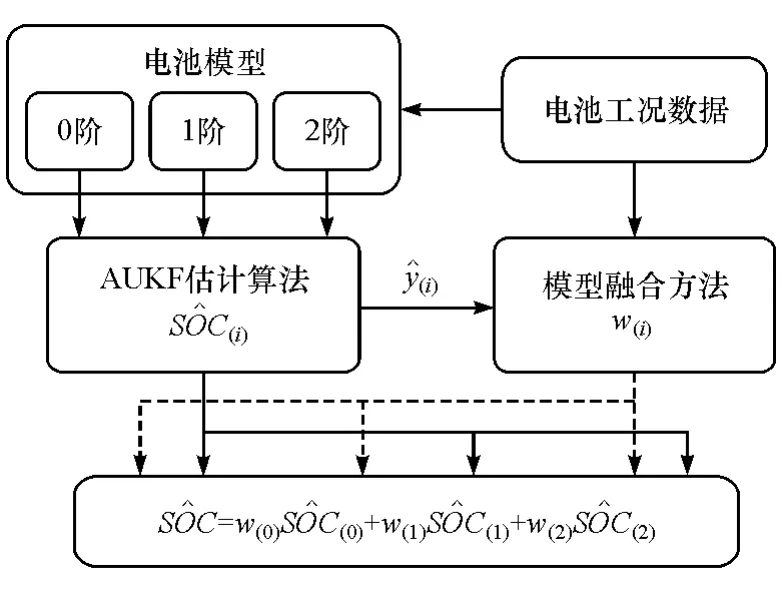
图3 基于模型融合的SOC估计算法示意图

4 结果与分析

本文中选用双登50A·h磷酸铁锂电池作为实验对象，电池参数如表1所示。电池实验平台由哈丁高低温试验箱、Arbin BTS 2000充放电机、Digatron BTS-600充放电机和上位机构成，如图4所示。上位机监控软件可以实时记录电池测试数据。本文中测试实验均在哈丁高低温试验箱25℃环境下进行。

表1 50A·h双登磷酸铁锂电池基本技术规格

图4 电池实验平台

电池模型离散时间方程的监测方程须将Uoc-SOC关系作为先验知识。本文中采用电池充放电静置实验求取开路电压均值的方法获取电池Uoc-SOC关系，具体方法如下:对实验电池充放电5A·h静置2h，测量电池端电压取平均值，并使用最小二乘法进行曲线拟合，拟合曲线如图5所示。开路拟合方程为

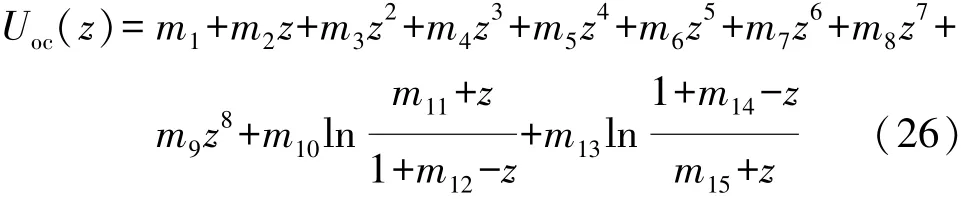
式中:mi(i＝1，2，…，15)为模型拟合参数，如表 2所示；z为电池的SOC值。

图5 电池开路电压

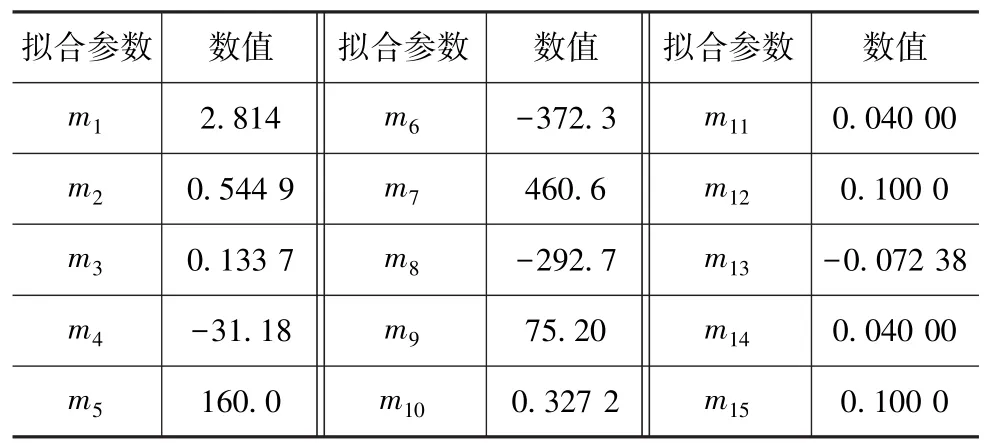
表2 开路电压拟合方程参数

本文中采用GA辨识电池模型参数，电池测试应用一种自定义脉冲工况[18]，如图6所示，该工况通过电动汽车系统建模，由车辆行驶工况逆推电池工况得到，更符合动力电池实际工作状态。不同阶次电池模型参数如表3所示。

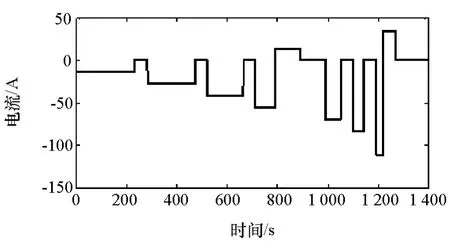
图6 自定义脉冲工况

对阶次为0，1，2的电池模型分别应用AUKF算法，并对算法的电池模型输出估计应用BIC考评，得到不同阶次电池模型的BIC，如图7所示。由BIC考评，BIC越小，电池模型阶次越优。图7中存在A，B，C 3类BIC最小片段，分别对应0，1，2阶电池模型为最优，可以看出单一模型阶次不能始终保持最优，有必要应用模型融合方法，使AUKF算法始终基于最优电池模型。

图8为AUKF算法基于不同阶次电池模型、模型融合的SOC估计与SOC测量值的比较，其中SOC初值设置为0.5。由图8放大区域可以看出，基于模型融合的SOC估计优于基于2阶电池模型的SOC估计，并实现了基于0阶次模型SOC估计到基于1阶次模型SOC估计的转换。由此可见，基于模型融合与AUKF算法的SOC估计算法可以实现最优模型阶次的选择与较高SOC的估计精度。基于不同阶次模型和模型融合的SOC估计误差分析如表4所示。

表3 电池模型辨识参数

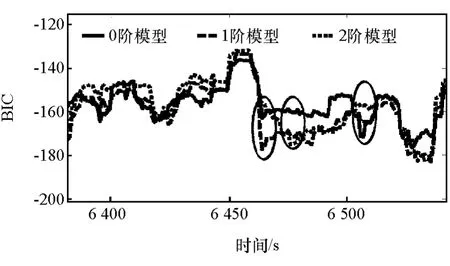
图7 电池模型BIC考评

图8 SOC估计比较

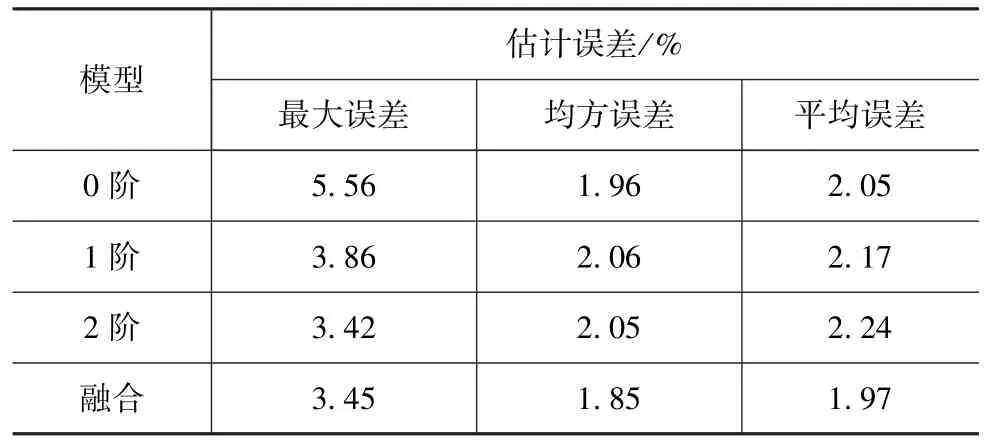
表4 SOC估计误差比较

5 结论

本文中提出了一种基于模型融合与自适应无迹卡尔曼滤波估计锂离子电池SOC估计方法。构建了锂离子电池模型，给出了模型参数辨识方法，建立了不同阶次电池模型融合方法，采用自适应无迹卡尔曼滤波对基于模型融合的SOC估计进行了仿真研究。结果表明，本文中提出的基于模型融合与自使用无迹卡尔曼滤波的SOC估计方法不仅能够选择最优模型阶次，而且能够得到精度较高的电池SOC估计值。

[1] 党杰，汤奕，宁佳，等.基于用户意愿和出行规律的电动汽车充电负荷分配策略[J].电力系统保护与控制，2015，43(16):8-15.

[2] 杨世春，麻翠娟.基于PNGV改进模型的SOC估计算法[J].汽车工程，2015，37(5):582-586.

[3] 付浪，杜明星，刘斌，等.基于开路电压法与卡尔曼滤波法相结合的锂离子电池SOC估算[J].天津理工大学学报，2015，31(6):9-13.

[4] 孙丙香，高科，姜久春，等.基于ANFIS和减法聚类的动力电池放电峰值功率预测[J].电工技术学报，2015，30(4):272-280.

[5] WAAG W，SAUER D U.Adaptive estimation of the electromotiveforce of the lithium-ion battery after current interruption for an accurate state-of-charge and capacity determination[J].Applied Energy，2013，111(4):416-427.

[6] 刘艳莉，戴胜，程泽，等.基于有限差分扩展卡尔曼滤波的锂离子电池SOC估计[J].电工技术学报，2014，29(1):221-228.

[7] SMITH K A，RAHN C D，WANG C Y.Control oriented ID electrochemical model of lithium-ion battery[J].Energy Conversion and Management，2007，48(9):2565-2578.

[8] SMITH K A，RAHN CD，WANGCY.Model-based electrochemical estimation and constraint management for pulse operation of lithium-ion batteries[J].Ieee Transactions on Control Systems Technology，2010，18(3):654-663.

[9] SHEN W X，CHAN CC，LOEWC，et al.A new battery available capacity indicator for electric vehicles using neural network[J].Energy Conversion and Management，2002，43(6):817-826.

[10] CHAU K T，WU K C，CHAN CC.A new battery capacity indicator for lithium-ion battery powered electric vehicles using adaptive neuro-fuzzy inference system[J].Energy Conversion and Management，2004，45(11-12):1681-1692.

[11] WAAG W，FLEISCHER C，SAUER D U.On-line estimation of lithium-ion battery impedance parameters using a novel varied-parameters approach[J].Journal of Power Sources，2013，237(3):260-269.

[12] WAAG W，SAUER D U.Adaptive estimation of the electromotive force of the lithium-ion battery after current interruption for an accurate state-of-charge and capacity determination[J].Applied Energy，2013，111(4):416-427.

[13] 程泽，董梦男，杨添剀，等.基于自适应混沌粒子群算法的光伏电池模型参数辨识[J].电工技术学报，2014，29(9):245-252.

[14] 冯飞，宋凯，逯仁贵，等.磷酸铁锂电池组均衡控制策略及荷电状态估计算法[J].电工技术学报，2015，30(1):22-29.

[15] 冯飞，逯仁贵，朱春波.一种锂离子电池低温SOC估计算法[J].电工技术学报，2014，29(7):53-58.

[16] 张齐东，黄学良，陈中，等.电动汽车电池更换站集群充电控制策略研究[J].电工技术学报，2015，30(12):447-453.

[17] MIRZAEE A，SALAHSHOOR K.Fault diagnosis and accommodation of nonlinear systems based on multiple-model adaptive unscented Kalman filter and switched MPC and H-infinity loop-shaping controller[J].Journal of Process Control，2012，22(3):626-634.

[18] LI Yong， WANG Lifang， LIAO Chenglin， et al.A model-based driving cycle test procedure of electric vehicle batteries[J].High Technology Letters，2014，20(3):308-314.

Estimation of Li-ion Battery SOC Based on Model Fusion and Adaptive Unscented Kalman Filtering Algorithm

Liu Weilong1，2， Wang Lifang1， Liao Chenglin1＆ Wang Liye1
1.Key Laboratory of Power Electronics and Electric Drives， Institute of Electrical Engineering， Chinese Academy of Science， Beijing 100190；2.University of Chinese Academy of Sciences，Beijing 100049

In order to enhance the SOC estimation accuracy of power battery in electric vehicles，the lithium-ion battery model and its parameter identification algorithm，adaptive unscented Kalman filtering(AUKF)algorithm and the SOC estimation algorithm based on battery model fusion are studied in this paper.A battery circuit model with clear physical meanings is established，a AUKF-based battery SOC estimation scheme is devised by using model parameter identification algorithm based on genetic algorithm，and a battery model fusion method is proposed based on Bayesian information criteria to fulfill battery SOC estimation based on model fusion.The results of simulation show the high accuracy of SOC estimation method proposed.

10.19562/j.chinasae.qcgc.2017.09.004

∗国家重点研发计划项目(2016YFB0100107和2016YFB0101800)和国家电网公司科技项目“电动汽车基础设施运行安全与互联互通技术”资助。

原稿收到日期为2016年9月9日，修改稿收到日期为2016年10月26日。

刘伟龙，博士，E-mail:zkylwl＠foxmail.com。