基于交互式多模型和容积卡尔曼滤波的汽车状态估计∗

张家旭，李 静

基于交互式多模型和容积卡尔曼滤波的汽车状态估计∗

张家旭1，2，李 静1

(1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022； 2.中国第一汽车集团技术中心，长春 130011)

基于UniTire轮胎模型建立了包含时变噪声统计特性的汽车动力学7自由度整车模型。针对系统状态噪声和观测噪声统计特性未知的问题，提出了一种基于交互式多模型和容积卡尔曼滤波(IMM-CKF)车辆状态估计算法。该算法采用包含不同系统状态噪声和观测噪声统计特性的汽车动力学模型作为交互式多模型算法的模型集，用容积卡尔曼滤波器对每个子模型的车辆状态进行估计，并使融合输出结果始终保持跟踪估计误差小的子模型输出。最后利用实车场地环境下多种驾驶工况的测试数据对IMM-CKF算法进行离线验证，并与容积卡尔曼滤波器的估计结果进行对比，结果表明其估计性能优于容积卡尔曼滤波器。

汽车动力学；容积卡尔曼滤波；交互式多模型；汽车状态估计

Keywords:vehicle dynamics； cubature Kalman filter； interactive multiple model； vehicle state estimation

前言

汽车的纵向和侧向速度是车辆主动安全系统中重要的控制变量，对于功能高度集成的电子稳定控制系统(electronic stability program，ESP)，车辆纵向和侧向速度是进一步确定控制逻辑中车轮滑移率、质心侧偏角等控制变量的重要参数，还是车载故障诊断系统中的关键技术之一，因此准确实时获取车辆的纵向和侧向速度是实现车辆主动安全控制的必要前提。由于技术和成本方面的原因，这些信息通常无法直接测量，由此衍生出的基于车载传感器获得的车辆状态信息进行汽车纵向和侧向速度估计成为近年来国内外研究的热点[1-3]。

文献[4]中应用无迹卡尔曼滤波器(unscented Kalman filter，UKF)对汽车状态进行估计，由于文中采用包含时不变噪声统计特性的非线性车辆动力学模型作为算法设计的标称模型，故不准确系统过程噪声和观测噪声统计特性会影响估计精度。文献[5]中采用3自由度的非线性车辆模型作为双扩展卡尔曼滤波器(dual extended Kalman filter，DEKF)设计的标称模型，并利用DEKF对车辆状态和路面附着系数进行估计，在迭代估计过程中需要计算系统状态方程和量测方程的雅可比矩阵，容易导致出错及估计器实时性降低。文献[6]中采用自适应神经模糊推理系统建立车辆的侧向加速度、横摆角速度、转向盘转角、纵向速度与质心侧偏角之间的非线性输入-输出关系，通过输入信号直接计算车辆的质心侧偏角，避免标称模型的不确定性对估计结果的影响，但该方法需要大量的训练数据进行自学习，且外延性差。文献[7]中设计非线性观测器估计车辆的纵向速度、侧向速度和路面附着系数，并构造李雅普诺夫函数证明系统的稳定性，但该方法未考虑标称模型的不确定性、外界扰动对估计精度和系统稳定性的影响。文献[8]中融合惯性传感器和GPS传感器的测量信息，采用自适应扩展卡尔曼滤波器估计车辆的质心侧偏角，由于传感器的成本较高，限制了其适用范围。因此，在设计车辆纵向和侧向速度估计器时，应充分考虑系统过程噪声和观测噪声的不确定性对估计精度的影响，以及最小化估计算法对硬件资源的需求。

与传统EKF相比，容积卡尔曼滤波器(cubature Kalman filter，CKF)具有估计精度高和实时性强的特点[9]。但二者均需要较精确的系数数学模型和噪声统计特性，否则会导致预测和估计精度降低甚至产生发散现象。为此，本文中将CKF与交互式多模型算法(interacting multiple model，IMM)结合形成一种交互式多模型容积卡尔曼滤波算法(IMM-CKF)，该算法采用包含不同系统状态噪声和观测噪声统计特性的7自由度车辆模型作为IMM的模型集，用CKF对每个子模型的车辆纵向和侧向速度进行估计，并使融合输出结果始终保持跟踪估计误差小的子模型输出。最后，在Matlab/Simulink环境下利用多种工况的实车场地试验数据进行离线验证，并与CKF的估计结果进行对比分析。结果表明，IMMCKF算法的估计性能优于CKF。

1 车辆动力学模型

1.1 整车模型

本文中采用7自由度车辆动力学模型作为车辆状态估计算法设计的标称模型，如图1所示，该模型包括车辆的纵向运动、侧向运动、横摆运动和4个车轮的回转运动。

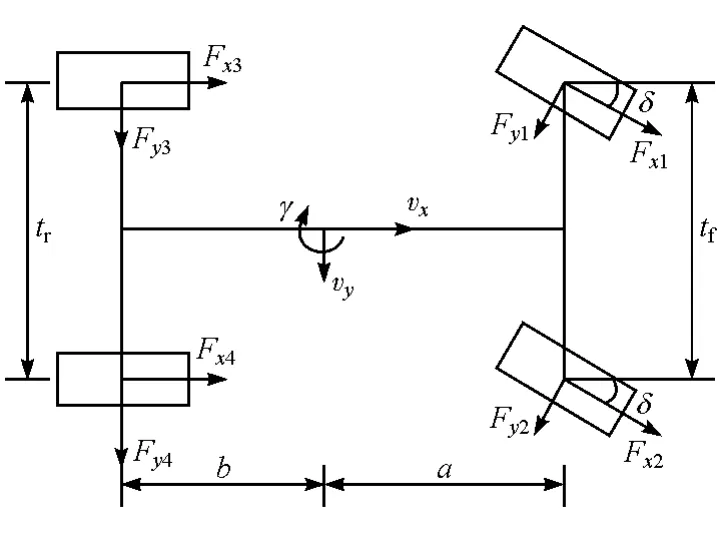
图1 7自由度车辆动力学模型示意图

对于图1所示的模型，车辆运动的微分方程为

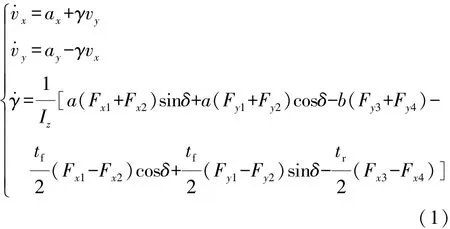
式中:vx为纵向速度；vy为侧向速度；ax为纵向加速度；ay为侧向加速度；γ为横摆角速度；Iz为整车绕垂直轴的转动惯量；Fx1，Fx2，Fx3和 Fx4分别为 4个车轮上的纵向力；Fy1，Fy2，Fy3和 Fy4分别为 4 个车轮上的侧向力；δ为前轮转角；tf和tr分别为前轮距宽和后轮距宽；a和b分别为整车质心到前后轴的距离。

忽略空气阻力的影响，根据达朗贝尔原理建立车辆加速度与轮胎力之间的关系:

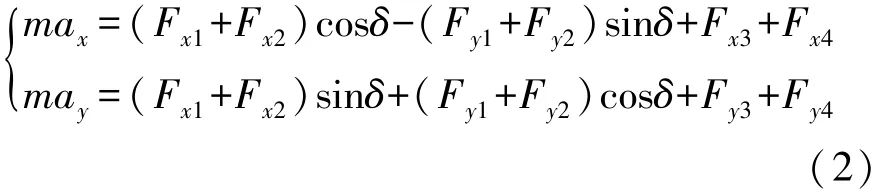
式中m为整车质量。

对于式(1)和式(2)中涉及的轮胎力，考虑其非线性动态特性，本文中采用郭孔辉院士提出的UniTire轮胎模型[10]来描述轮胎的纵向力和侧向力。

首先定义轮胎的纵向滑移率Sx、侧向滑移率Sy与无量纲的相对纵向滑移率φx、相对侧向滑移率φy和相对总滑移率φ:

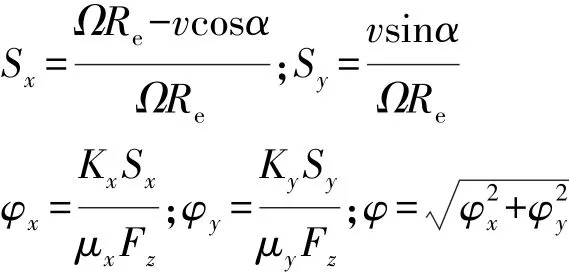
式中:Ω为轮胎滚动角速度；v为轮心的移动速度；α为轮胎侧偏角；Re为有效滚动半径；Kx和Ky分别为轮胎的纵向刚度和侧偏刚度；μx和μy分别轮胎接触印迹内纵向和侧向摩擦因数；Fz为轮胎所受的垂直载荷。

轮胎所受的纵向力Fx和侧向力Fy[10]可表示为

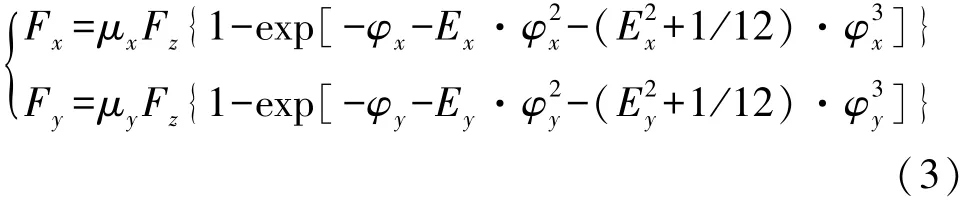
式中Ex和Ey为UniTire轮胎模型的待匹配参数，可通过轮胎试验数据辨识得到。

1.2 包含噪声的车辆状态方程

本文中讨论的车辆状态估计问题根据车载传感器测量得到的纵向加速度ax、侧向加速度ay、横摆角速度γ、前轮转角δ(由转向盘转角间接测量得到)和轮速[w1w2w3w4]T信息，估计车辆的纵向速度vx、侧向速度vy和横摆角速度γ。其中，将γ作为被估计状态是为了充分利用其测量信息。因此，根据7自由度车辆动力学模型，设状态向量为

系统输入为

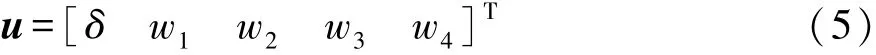
观测向量为

由式(1)～式(3)和前向欧拉积分法可得车辆系统离散化的状态方程和观测方程为

式中wk和vk分别为状态估计的过程噪声和观测噪声，二者相互独立，均为零均值的高斯白噪声，设它们的协方差矩阵分别为Q和R。

研究发现[11]:在过程噪声协方差Q一定的情况下，较大的测量噪声协方差R会减小过程噪声对滤波算法估计精度的影响，但会降低其收敛速度；在测量噪声误差协方差R一定的情况下，较大的过程噪声协方差Q会减少滤波算法的时间延迟，但会加大测量噪声对其估计精度的影响，使估计误差变大。为实时保持滤波器的最优性能，避免滤波发散，需要根据不同的环境调试噪声参数。本文中采用一组并行的滤波器，其中每个滤波器采用不同的噪声参数，并根据观测量单独进行滤波，然后根据滤波残差对各个滤波器的估计值进行加权。

2 容积卡尔曼滤波器

由Arasaratnam等人提出的CKF算法基于球面径向积分准则，利用2n个具有相同权重的容积点对状态的概率密度分布函数进行逼近，避免复杂的雅克比矩阵的运算，提高了滤波的精度和稳定性。CKF算法步骤如下[12]。

步骤1:时间更新

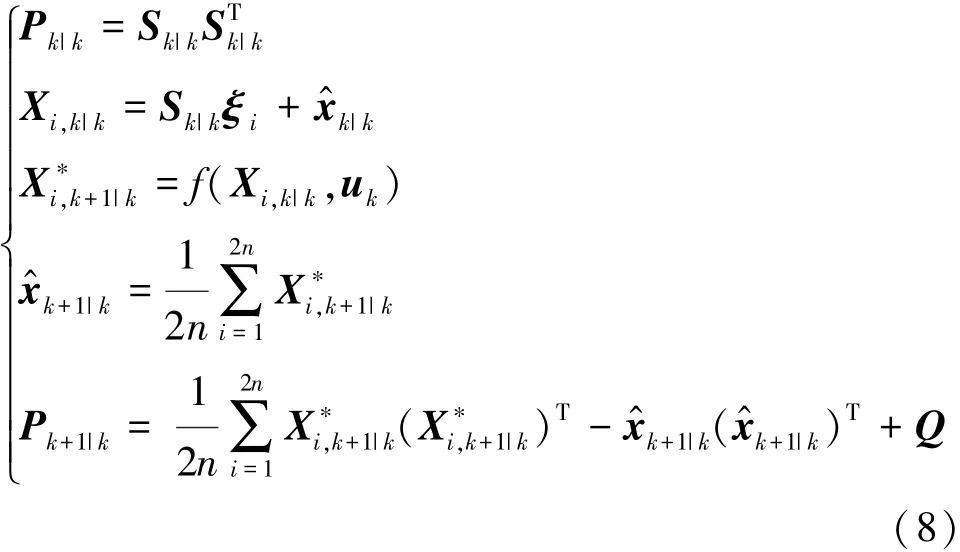
式中:Sk｜k为 Pk｜k的平方根；ξi＝ n[1]i，[1]i为基本容积点；Xi，k｜k为计算的容积点；X∗i，k+1｜k为通过状态方程传播输出的容积点；x＾k+1｜k为状态向量的一步预测值；Pk+1｜k为误差协方差一步预测值。

步骤2:量测更新

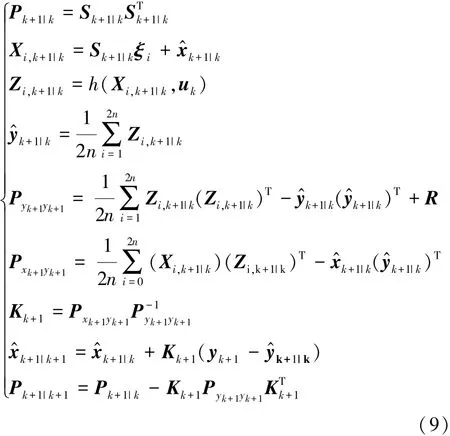
式中:Sk+1｜k为 Pk+1｜k的平方根；Xi，k+1｜k为计算的容积点；Zi，k+1｜k为通过测量方程传播输出的容积点；y＾k+1｜k为测量的一步预测值；Pyk+1yk+1为新息协方差矩阵；Pxk+1yk+1为交叉协方差矩阵的一步预测值；Kk+1为卡尔曼增益矩阵；x＾k+1｜k+1为当前时刻的状态向量；Pk+1｜k+1为当前时刻的误差协方差矩阵。

3 交互式多模型容积卡尔曼滤波算法

交互式多模型算法具有自适应的特点，能够有效地对每个子模型的概率进行实时调整，并根据模型转移矩阵使融合输出结果始终保持跟踪误差小的子模型输出[13]。 定义 M＝{m1，m2，…，mN}为描述系统的模型集合，k时刻模型mi出现的条件概率为μi，k＝p{mi，k，yk}，k 时刻到 k+1 时刻从模型 mi到模型 mj的转移概率为 pij＝p{mj，k+1｜mi，k}，交互式多模型容积卡尔曼滤波算法的具体计算步骤如下。

步骤1:模型mi与模型mj的混合概率ui/j，k可表示为式中 μj，k+1｜k为模型 mj的预报概率。

步骤2:输入交互

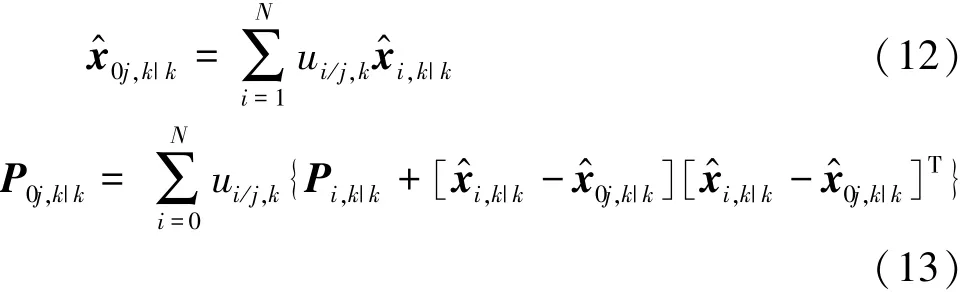
步骤3:采用式(8)和式(9)对每个模型进行时间更新和量测更新。

步骤4:模型概率更新

模型似然:

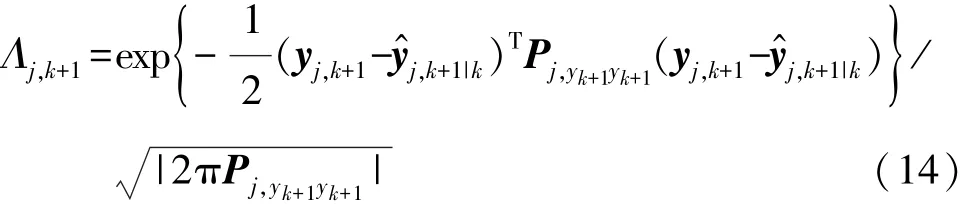
模型概率:

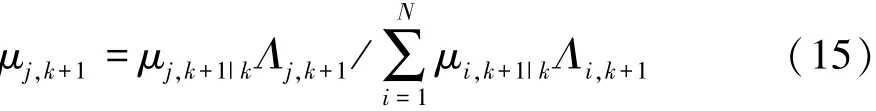
步骤5:经滤波后进行组合，将每个模型的输出结果组合得到最终的滤波输出交互:

4 实车试验验证

为了验证IMM-CKF算法对车辆状态估计的准确性和可靠性，利用某三厢轿车进行操纵稳定性场地试验，该试验车安装有轮速传感器、转向盘转角传感器、GPS/INS惯性组合导航系统RT3000和转向机器人等，数据采集仪的采样频率为1 000Hz。试验车的参数如表1所示。

表1 车辆参数

考虑车辆行驶中的系统过程噪声和观测噪声的不确定性，引入一组系统过程噪声和观测噪声，得到一组模型集 M＝{m1，m2，m3}。

设定模型m1是噪声较小的情况，其过程噪声和观测噪声协方差为

设定模型m2是噪声适中的情况，其过程噪声和观测噪声协方差为

设定模型m3是噪声较大的情况，其过程噪声和观测噪声协方差为

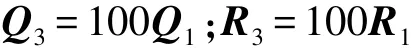
设定3个模型的马尔科夫转移概率矩阵为

考虑车辆侧倾角的影响，对GPS/INS惯性组合导航系统RT3000测得的车辆侧向加速度进行修正:

式中:aym为GPS/INS惯性组合导航系统RT3000测量的车辆侧向加速度；φ为GPS/INS惯性组合导航系统RT3000测量的车辆侧倾角；ay为车辆侧向加速度的修正值。

设定车辆质心处的纵向速度、侧向速度和横摆角速度3个状态量的估计初始值为GPS/INS惯性组合导航系统RT3000记录的试验初始值。在Matlab/Simulink环境下实现IMM-CKF算法，并通过离线仿真将实车试验数据与IMM-CKF算法的估计结果进行对比，如图2所示。

图2 算法验证流程

4.1 斜坡输入试验

在干燥、平坦而清洁的水泥试验场地，车速保持80km/h，利用转向机器人进行斜率为40°/s，峰值为160°的转向盘斜坡输入，估计输入如图3(a)所示，试验测量值、CKF算法和IMM-CKF算法的估计结果如图3(b)～图3(d)所示。该试验可使车辆随着转向盘转角增加而逐渐进入极限工况，且轮胎由线性工作区逐渐过渡到非线性工作区，从而导致车辆标称模型的误差增加。研究表明[14-16]:标称模型的误差可以折算成其系统噪声，且标称模型的系统噪声表征外部真实系统噪声的精确程度是影响系统状态量的估计精度的重要因素。由图3(b)～图3(d)可见:在系统噪声增加时，CKF算法对纵向速度和侧向速度的估计偏差逐渐增大，但IMM-CKF算法可根据每个子模型的目标估计状态和系统的当前测量值对其模型概率进行实时调整，并通过马尔科夫转移矩阵Φ使融合输出结果始终平滑地保持跟踪误差小的子模型输出，从而使该算法对对纵向速度和侧向速度的估计保持较高的估计精度；对于横摆角速度的估计，CKF算法和IMM-CKF算法均保持较高的估计精度。

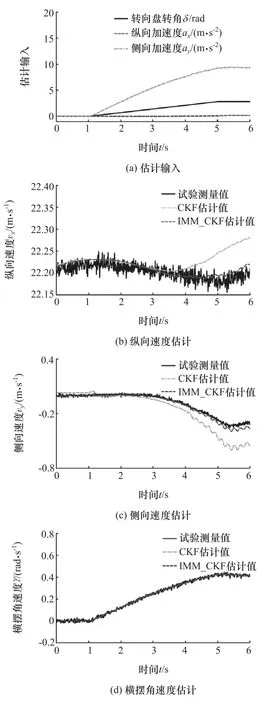
图3 斜坡输入试验的估计结果对比分析

4.2 急剧双移线试验

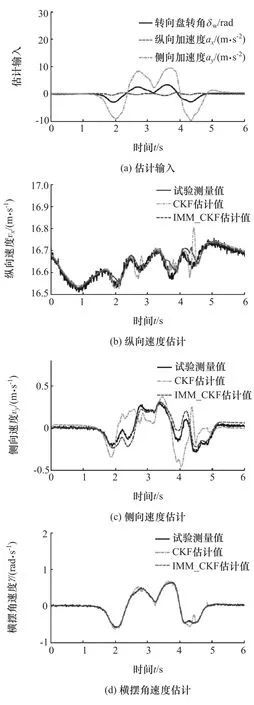
图4 急剧双移线试验的估计结果对比分析

在干燥、平坦而清洁的水泥试验场地进行急剧双移线试验，试验车速为60km/h，试验驾驶员使车辆不接触标桩条件下通过双移线通道，估计输入如图4(a)所示，试验测量值、CKF算法和IMM-CKF算法的估计结果如图4(b)～图4(d)所示。该试验工况用于验证算法在车辆状态快速改变时，对车辆的纵向速度、侧向速度和横摆角速度的估计精度。结果表明:IMM-CKF算法对纵向速度和横摆角速度的估计均取得较好的效果，但CKF算法对二者的估计存在小幅度的波动；对于侧向速度，IMM-CKF算法在转向盘转动过程中的估计结果与试验测量值之间存在一定幅值的偏差，而CKF算法的估计结果存在较大的波动。

4.3 正弦延迟试验

在干燥、平坦而清洁的水泥试验场进行正弦延迟试验，试验车辆以(80±2)km/h的速度匀速直线行驶，待车速稳定后转向机器人启动工作程序，以0.7Hz的频率、180°的峰值进行正弦-停顿模式的转向盘输入，在负波峰位置保持500ms的停顿，估计输入如图5(a)所示，试验测量值、CKF算法和IMMCKF算法的估计结果如图5(b)～图5(d)所示。结果表明:对纵向速度和横摆角速度，IMM-CKF算法均取得较好的估计效果，而CKF算法对二者的估计结果在转向盘保持阶段存在一定幅值的波动；对侧向速度，IMM-CKF算法在其峰值处的估计值与试验测量值之间存在较小幅度的偏差，但总体的估计结果满足工程需要，而CKF算法对其估计结果在转向盘转动过程中与试验测量值之间存在一定幅值的偏差，在转向盘保持过程中存在一定幅值的波动。

图5 正弦延迟试验的估计结果对比分析

上述3个试验工况下，在车辆速度较大时执行快速转向动作，将导致较大的车辆侧倾运动和轮胎进入非线性工作区域(车辆侧向加速度已达到路面附着极限)，从而引起车辆参数摄动和模型误差增大。这些扰动会引起系统过程噪声和观测噪声的不确定性，相对于CKF算法，IMM-CKF算法包含不同过程噪声和观测噪声协方差的子模型，且其融合输出总是保持跟踪估计误差小的子模型输出，有效抑制系统的不确定过程噪声和观测噪声对车辆状态估计结果的影响，提高系统状态量的估计精度，增加系统的鲁棒性。

5 结论

(1)本文中结合容积卡尔曼滤波器与交互式多模型算法，提出交互式多模型容积卡尔曼滤波算法来估计车辆状态。经试验验证，该算法对车辆状态的估计具有良好的性能。

(2)将非线性7自由度车辆动力学模型作为标称模型的IMM-CKF算法可较为准确地估计车辆纵向速度、侧向速度和横摆角速度。特别是在系统过程噪声和观测噪声不确定时，该算法的估计精度依然较高，具有较强的鲁棒性。

[1] 沈法鹏，赵又群，孙秋云，等.基于IEKF-APF算法的汽车状态估计[J].机械工程学报，2014，50(22):136-141.

[2] ACARMAN T.Observation of vehicle states by using steering wheel angle and wheel angular speeds[C].IEEE International Conference on Vehicular Electronics and Safety.Columbus， OH，2008:189-194.

[3] BEST M C， GORDON T J， DIXON P J.An extended adaptive Kalman filter for real-time state estimation of vehicle handling dynamics[J].Vehicle System Dynamics，2000，34(1):57-75.

[4] ANTONOV S，FEHN A，KUGI A.Unscented Kalman filter for vehicle state estimation[J].Vehicle System Dynamics，2011，49(9):1497-1520.

[5] ZONG Changfu， HU Dan， ZHENG Hongyu.Dual extended Kalman filter for combined estimation of vehicle state and road friction[J].Chinese Journal of Mechanical Engineering，2013，26(2):313-324.

[6] BEATRIZ L B，MARIA J L，ANTONIO G，et al.Sideslip angle estimator based on ANFIS for vehicle handling and stability[J].Journal of Mechanical Science and Technology，2015，29(4):1473-1481.

[7] SUN F，HUANG X H，JOACHIM R，et al.Vehicle state estimation for anti-lock control with nonlinear observer[J].Control Engineering Practice，2015，43(2015):69-84.

[8] MARIO H，JOSKO D，DANIJEL P，et al.Adaptive EKF-based estimator of sideslip angle using fusion of inertialsensors and GPS[C].SAE Paper 2011-01-0953.

[9] FERNANDEZ-PRADES C，VILA-VALLS J.Bayesian nonlinear filtering using quadrature and cubature rules applied to sensor data fusion for positioning[C].IEEE International Conference on CommunicationsRadar Science and Technology， Castelldefels， Spain，2010:1-5.

[10] GUO K H，LU D.UniTire:unified tire model for vehicle dynamic simulation[J].Vehicle System Dynamics，2007，45(S1):79-99.

[11] 刘铮.UKF算法及其改进算法的研究[D].长沙:中南大学，2009.

[12] ARASARATNAM I，HAYKIN S.Cubature Kalman filters[J].IEEE Transactions on Automatic Control，2009，54(6):1254-1269.

[13] LI X R，JILKOV V P.A survey of maneuvering target trackingpart five:multiple-model methods[J].IEEE Transactions on Aerospace and Electronic Systems，2005，41(4):1225-1321.

[14] XIONGK，ZHANGH Y，CHEN CW.Performance evaluation of UKF-based nonlinear filtering[J].Automatica，2006，42(2006):261-270.

[15] WU Y X，HU D W，HU X P.Comments on“Performance evaluation of UKF-based nonlinear filtering”[J].Automatica，2007，43(2007):567-568.

[16] XIONG K，ZHANG H Y，CHAN C W.Author's reply to“Comments on‘Performance evaluation of UKF-based nonlinear filtering’”[J].Automatica，2007，43(3):569-570.

Vehicle State Estimation Based on Interactive Multiple Model and Cubature Kalman Filter

Zhang Jiaxu1，2＆ Li Jing1
1.Jilin University， State Key Laboratory of Automotive Simulation and Control， Changchun 130022；2.Research and Development Center， China FAWGroup Corporation， Changchun 130011

A 7-DOF vehicle dynamics model with time-varying noise statistical characteristics is established based on UniTire model.For the unknown system statistical characteristics of state noise and observation noise，a vehicle state estimation algorithm based on interactive multiple model(IMM)and cubature Kalman filter(CKF)is proposed.The algorithm adopts the vehicle dynamics model with different system statistical characteristics of state noise and observation noise as model set of IMM algorithm and uses CKF to estimate the vehicle state of each submodel to make fusion output results constantly track the sub-model output with small estimation error.Finally，the measured data of several driving conditions under real vehicle test environment to conduct off-line verification on IMM-CKF algorithm with the results compared with that using CKF estimation.The outcomes show that the estimation performance of IMM-CKF algorithm is superior to that of CKF.

10.19562/j.chinasae.qcgc.2017.09.001

∗国家自然科学基金(51275206)资助。

原稿收到日期为2016年9月20日。

张家旭，博士研究生，E-mail:zhjx_686＠163.com。