智能汽车纵向控制校正与切换方法研究∗
2017-10-12崔文锋张立增
管 欣,崔文锋,贾 鑫,张立增
智能汽车纵向控制校正与切换方法研究∗
管 欣,崔文锋,贾 鑫,张立增
(吉林大学,汽车仿真与控制国家重点实验室,长春 130022)
基于对真实驾驶员纵向控制行为的分析,提出一种智能汽车纵向加速度跟随控制的校正策略。将加速度作为外环实施闭环控制,为确保开环前向通道特性为低频下的理想1系统,用车辆纵向动力学的等效1阶惯性模型的逆模型作为前馈。采用一种拟人化分相逻辑解决加速踏板与制动踏板的切换问题。该校正策略模拟人的控制行为,无需准确的车辆参数,即能在车辆运行全速度范围内实施控制,适用于stop-and-go系统的应用。仿真结果表明,采用该校正策略后,加速度跟随响应快,加速踏板与制动踏板切换平稳,符合真实驾驶员操作行为。
智能汽车;加速度控制;分相控制;切换逻辑
Keywords:intelligent vehicle;acceleration control;split phase control;switching logic
前言
智能汽车的驾驶行为分为信息感知、轨迹决策和操作校正3个环节,汽车纵向操作校正是考虑汽车动力学特性和驾驶员本身的滞后特性等,对决策出来的预瞄加速度进行一定的校正并做出对加速踏板与制动踏板的实际操作动作的过程[1]。纵向加速度校正是智能车控制的基础,其性能将影响智能驾驶整体性能,并影响车内乘员的体验。由于纵向控制需要采用加速踏板与制动踏板两套操纵机构,加速度跟随控制还需要解决两套机构之间的切换问题[2]。
目前,多数纵向控制策略通过车辆逆模型前馈和PI/模糊PID反馈控制实现踏板控制[2-6],控制效果对逆模型精度依赖较大。文献[5]中将车辆纵向加速度与车速、节气门开度和制动压力的关系根据动力学方程离线做成查询表,避免了控制器中动力学的实时计算,但需要大量标定工作。文献[6]中采用模糊PID控制方法跟随目标速度,有效提高了系统在大跟随误差情况下的控制鲁棒性。为适应汽车纵向动力学的不确定性,文献[7]中采用基于鲁棒控制的多模型分层切换控制,文献[8]中根据不同驾驶工况,将车辆控制分成6种模式,不同模式侧重的控制目标量不同,改善了系统整体控制品质。文献[9]中通过动力学模型分析车速对加速踏板开度的传递函数形成预期操纵并通过反馈补偿得到最终踏板开度,但预期操纵需要预知未来时刻的期望速度。文献[10]中采用迭代学习控制方法,可通过离线迭代学习得到最优控制器参数,无须准确的车辆模型,实现免匹配设计。文献[11]中采用自学习控制方法,实现了在线学习对象的行为特性,实时调节控制器参数。加速踏板与制动踏板之间的切换大部分是以松油门滑行时的减速度曲线为分界线,并通过增加迟滞环节来防止加速踏板与制动踏板之间的频繁切换[2-6],这种固定的分界使得车质量、风阻和道路坡度变化时可能会导致误判。
真实驾驶员在驾驶汽车时不需要知道车辆准确参数,且能够驾驶多种性能不同的车辆。本文中通过分析真实驾驶员的纵向控制行为,探索一种无需知道准确车辆参数,就能较好实现车辆纵向加速度跟随控制的方法。该方法首先将车辆纵向加速度作为外环,实施闭环控制,然后将加速度对踏板开度的响应等效成1阶惯性环节,并将该环节的逆模型作为前馈,从而将控制系统开环前向通道响应校正为低频下的理想1系统,减小了闭环控制的负担。考虑到车辆纵向控制需要加速踏板与制动踏板两套控制机构,通过拟人化分相思想[12]解决两套机构之间的切换问题。
1 控制器总体架构
1.1 驾驶员纵向控制行为分析
首先,驾驶员在进行纵向控制时能根据期望加速或减速强度直接产生一个预期的加速踏板或制动踏板控制量[9],而且熟练的驾驶员会根据车辆性能修正自己预期控制的大小[13],这种能力使得同一驾驶员能够驾驶不同性能的车辆。
其次,真实驾驶员不会采用频繁调整踏板的方式来控制车辆[13]。一方面是由于驾驶员对控制目标量往往没有太精确的要求,只要满足一定范围就不会继续调整踏板开度;另一方面是由于人对加速度感受精度低,无法为了精确跟随目标量而对踏板进行频繁调整。人的这种特点可能无法达到较高跟随精度,但对车辆的控制却更加平顺,高频操作踏板反而会增大车辆纵向闯动。
以上分析是真实驾驶员纵向控制行为的重要特点,也是本文中提出的控制策略要达到的目标。
1.2 控制器结构
基于以上分析,本文中提出的控制策略如图1所示。

图1 纵向加速度控制器框图
校正模块为被控车辆的1阶等效系统的逆系统,校正模块反映驾驶员对车辆性能的理解而产生踏板控制量。反馈控制以目标加速度为控制目标量,通过PID控制补偿校正控制的误差。
分相模块用于在加速踏板控制和制动踏板控制之间进行切换。同时,考虑车辆在平路面上滑行时受到的空气阻力和滚动阻力所引起的车辆滑行减速度,PID控制的输出量fR减扣掉滑行减速度arx作为前馈校正输入量。
执行特性环节表达执行机构的响应滞后。
2 前馈校正
驾驶员对车辆性能的了解过程本质上是对车辆性能参数的识别过程。本节通过车辆纵向动力学模型,分析汽车目标加速度与期望踏板开度之间的关系。
2.1 加速踏板前馈校正
实际汽车响应都可用其低阶等效系统来近似描述[13],本文中采用1阶系统来描述车辆加速度对加速踏板响应:

式中:a为车辆加速度;αThr为加速踏板开度;kd为加速度对加速踏板响应的增益;Tdd为加速度响应的滞后时间常数。
式(1)所描述系统的低频区等效逆系统为

式中:αcThr为加速踏板校正输出量;Tfd为保证分子部分物理可实现而加入的1阶滤波器时间常数;Kd=1/kd。
式(2)即为加速踏板前馈校正环节的结构。
2.2 kd标定
由于汽车传动系的强非线性,kd随车速和加速踏板开度的不同而不同,需要通过标定得到kd在不同工况下的取值。标定方法是将车辆在水平路面上不同车速下空油门滑行,当滑行减速度趋于稳定后再施加加速踏板阶跃输入,车辆加速度会在短时间内达到稳定值,取该稳定值与滑行减速度绝对值之和与加速踏板阶跃幅值之比作为kd在该工况下的大小,如图2所示。同时,加速度响应到90%稳态值的时间即为Tdd。

图2 kd随车速和加速踏板开度变化关系
2.3 制动踏板前馈校正
与驱动相同,制动系统也用等效1阶惯性环节描述:

式中:αBrk为制动踏板开度;kb为加速度对制动踏板响应的增益;Tdb为制动时加速度响应的滞后时间常数。
取其低频区等效逆系统:
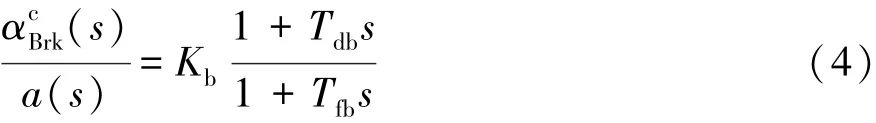
式中:αcBrk为制动踏板校正输出量;Tfb为保证分子部分物理可实现而加入的1阶滤波器时间常数;Kb=1/kb。
式(4)即为制动踏板前馈校正环节的结构。
2.4 kb标定
kb的获取方法与加速踏板前馈校正相同,将车辆在不同车速下空油门滑行,当滑行减速度趋于稳定后再施加制动踏板阶跃输入,取车辆加速度稳态值与滑行减速度绝对值之和与制动踏板阶跃幅值之比作为kb在该工况下的大小,如图3所示。加速度响应到90%稳态值的时间即为Tdb。
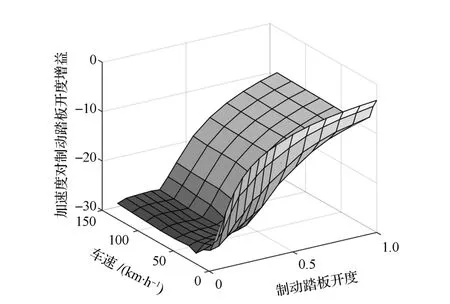
图3 kb随车速和制动踏板开度变化关系
3 反馈控制
前馈校正会由于建模假设及外界干扰等因素导致校正存在误差,故在加速度控制最外环采用加速度反馈控制。反馈控制采用抗积分饱和PID算法:
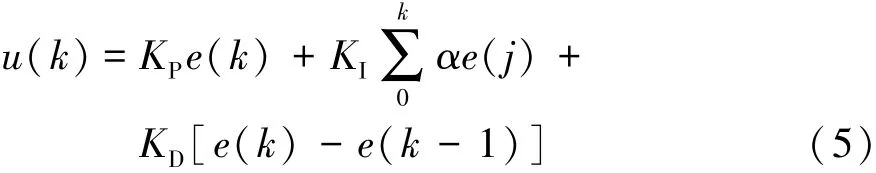
式中:e为目标加速度与实际加速度的偏差;u为PID控制器的输出;KP为比例系数;KI为积分系数;KD为微分系数;α为逻辑标识量。
当 u(k-1)≥umax时,α = 0;当 u(k-1)<umax时,α = 1,umax= 1。
4 拟人化分相逻辑
根据行驶工况不同,加速度跟随控制需要在加速踏板和制动踏板两套控制机构之间切换。本文中分析真实驾驶员切换的逻辑,通过分相思想设计了拟人化分相逻辑解决切换问题,能够自动适应坡度变化或风阻变化等干扰。
真实驾驶员驾驶汽车时,不会在加速踏板和制动踏板之间频繁切换。同时,车辆的纵向动力学响应滞后比较大,也不可能通过频繁切换来达到有效的控制。因此,真实驾驶员开车时明显存在3个相:驱动相、制动相和滑行相,滑行相中既不采用加速踏板控制,也不采用制动踏板控制。
本文中模拟人的这种驾驶行为,将加速度跟随控制分为驱动相、制动相和滑行相3个相。驱动相中仅采用加速踏板控制,制动相中仅采用制动踏板控制,滑行相中加速踏板和制动踏板都不控制。
车辆在平路上匀速行驶时,除了加速需要的驱动力,车辆还受到滚动阻力和空气阻力:

式中:arx为汽车滑行阻力减速度;Ff为滚动阻力;Fw为空气阻力;m为汽车质量。
空气阻力和滚动阻力随着车速不同而变化,但这两个阻力无需通过计算获得,只需通过国标空挡滑行实验,记录不同车速下车辆减速度的大小,即可得到不同速度下的滑行减速度。
为避免不必要的混淆,把汽车加速度PID闭环反馈控制的输出量称作比力,表示需要汽车驱动或制动系统作动产生的每单位质量的驱动或制动力,与加速度同量纲。闭环控制输出比力减扣汽车滑行阻力减速度得到的f作为汽车加速度闭环控制实际需要的汽车驱动或制动比力。将f作为前馈校正的目标量,同时作为分相的判据。

式中f为闭环控制输出比力与滑行阻力减速度之差。
拟人化分相逻辑当f大于一定的正阈值fd时,进入驱动相;当f小于一定的负阈值fb时,进入制动相;否则进入滑行相。fb和fd的大小代表不同驾驶员对滑行需求的强烈程度,这两个数值越大,表示滑行时允许的加速度跟随误差越大。由于反馈控制的存在,加速度跟随误差最终会导致f超过这两个阈值进入驱动相或制动相,因而能够适应车辆在不同车速下及受到坡度或风阻变化等干扰情况下的加速踏板与制动踏板的切换处理。
5 仿真验证
本文中采用文献[14]中开发的品质动力学模型,在Simulink中搭建加速度跟随控制算法,在多种工况下对控制策略进行验证。
执行特性用纯时延和1阶惯性滞后[13]表示:

式中:Gd为滞后环节;td为控制周期滞后;th为做动器响应滞后时间常数。本文中td= 0.001,th= 0.01。
以既定目标车速为基础设计仿真工况,目标车速与实际车速之差作为目标加速度。目标加速度生成模块如图4所示。图中,uR为目标速度,u为实际速度,aRx为目标加速度。

图4 目标加速度生成模块
5.1 斜坡工况
目标速度斜坡变化,模拟驾驶员正常加速与减速过程,仿真结果如图5所示。由图可见,车辆能够很好地跟随目标加速度,踏板变化平稳,加速踏板与制动踏板的切换符合真人的操作行为,车辆速度变化平稳,没有明显超调。
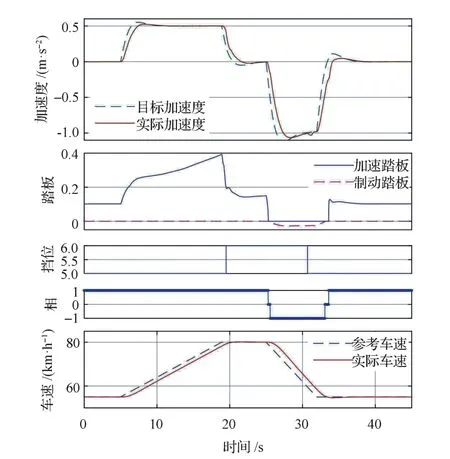
图5 斜坡工况仿真结果
5.2 滑行工况
目标车速以接近滑行减速度缓慢下降,检验加速踏板和制动踏板的切换逻辑,仿真结果如图6所示。由图可见,减速开始阶段车辆首先进入滑行相,此时加速度跟随误差不断变大,当跟随误差超过fb后进入制动相,施加制动控制,保证车辆速度跟随误差和加速度跟随误差在允许范围内,与真实驾驶员的控制行为相符。
5.3 复杂工况
目标车速参考国V市郊运转循环工况变化,模拟复杂环境下的驾驶过程,仿真结果如图7所示。由图可见:纵向车速能够一直很好地跟随目标车速,直至停车;加速度跟随误差维持在较小水平,踏板变化平稳,加速踏板和制动踏板切换符合真实驾驶员控制行为。
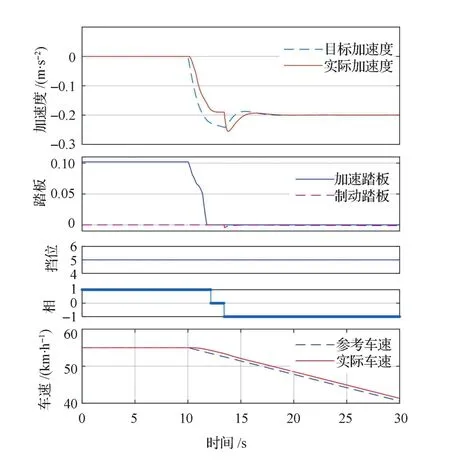
图6 滑行工况仿真结果

图7 复杂工况仿真和实验结果
6 结论
从分析真实驾驶员控制行为的角度,提出了本文中的控制策略。将驾驶员对车辆性能的理解通过车辆动力学模型的等效1阶惯性模型的逆模型来描述,符合真实驾驶员控制行为。
通过拟人化分相逻辑将车辆控制分成3个相,实现加速踏板与制动踏板的切换,并且能够适应环境参数的变化,在整个速度控制范围内都能实现相的合理切换。
控制策略不需要车辆准确参数,能够在全速度范围内实施控制,适用于stop-and-go控制。
仿真结果验证了本文中提出的控制策略的有效性。
[1] GUAN Hsin, GAO Zhenhai, GUO Konghui, et al.A driver direction control model and its application in the simulation of driver-vehicle-road closed-loop system[C].SAE Paper 2000-01-2184.
[2] YI K, HONG J, KWON Y D.A vehicle control algorithm for stopand-go cruise control[C].Proc Instn Mech Engrs,2001, 215(10):478-482.
[3] LU Xiaoyun,HEDRICK Karl.Heavy-duty vehicle modelling and longitudinal control[J].Vehicle System Dynamics, 2005,43(9):653-669.
[4] MOON Seungwuk,YI Kyongsu.Human driving data-based design of a vehicle adaptive cruise control algorithm[J].Vehicle System Dynamics, 2008, 46(8):661-690.
[5] 马国成,刘昭度,王宝锋,等.驾驶员辅助系统中自适应加速度跟随控制器的设计[J].汽车工程,2015,37(12):1453-1458.
[6] JIN X,SU Z,ZHAO X,et al.Design of a fuzzy-PID longitudinal controller for autonomous ground vehicle[C].IEEE International Conference on Vehicular Electronics& Safety,2011:269-273.
[7] 高锋,李家文,李克强,等.汽车纵向加/减速度多模型分层切换控制[J].汽车工程,2007,29(9):804-808.
[8] 裴晓飞,刘昭度,马国成,等.汽车自适应巡航系统的多模式切换控制[J].机械工程学报,2012,48(10):96-102.
[9] MITSCHKE Manfred,WALLENTOWITZ Henning.汽车动力学[M].4版.陈荫三,余强,译.北京:清华大学出版社,2009.
[10] 王竣.自适应巡航控制系统多目标感知决策控制算法研究[D].长春:吉林大学,2015.
[11] 严伟.仿驾驶员速度跟随行为的自适应巡航控制算法研究[D].长春:吉林大学,2016.
[12] 管欣,崔文锋,贾鑫.车辆纵向速度分相控[J].吉林大学学报, 2013,43(2):273-277.
[13] 郭孔辉.汽车操纵动力学原理[M].南京:江苏科学技术出版社,2011.
[14] 詹军,管欣,杨得军,等.ADSL驾驶模拟器动力学模型的改进与验证[J].江苏大学学报,2010,31(3),283-287.
A Research on Longitudinal Control Correction and Switching Scheme for Intelligent Vehicles
Guan Xin,Cui Wenfeng,Jia Xin& Zhang Lizeng
Jilin University, State Key Laboratory of Automotive Simulation and Control, Changchun 130022
Based on the analysis on the longitudinal control behavior of real drivers,a correction strategy for the longitudinal acceleration following control of intelligent vehicle is proposed.With acceleration as outer loop to fulfill closed-loop control,and the inverse model of the equivalent first-order inertia model in vehicle longitudinal dynamics is taken as feedforward to ensure that the open-loop forward channel characteristics are ideal 1 system at low frequency.An anthropomorphized phase split logic is adopted to switch between accelerating and braking pedals.The correction strategy proposed simulates human control behavior to fulfill vehicle control in whole speed range with no need of accurate vehicle parameters,suitable for the control of stop-and-go system.Simulation results demonstrate fast response in acceleration following, smooth switching between accelerating and braking pedals, tallying with the operation behavior of real drivers.
10.19562/j.chinasae.qcgc.2017.09.011
∗复杂交通环境下智能汽车主动安全控制性能主客观评测方法与准则研究联合基金项目(U1664261)资助。
原稿收到日期为2017年4月7日,修改稿收到日期为2017年6月5日。
贾鑫,博士,副教授,E-mail:jiaxin@jlu.edu.cn。
