大变形太阳电池阵展开的多体动力学分析

史加贝，刘铸永，洪嘉振

(上海交通大学船舶海洋与建筑工程学院,上海 200240)

大变形太阳电池阵展开的多体动力学分析

史加贝，刘铸永，洪嘉振

(上海交通大学船舶海洋与建筑工程学院,上海 200240)

由于存在大变形、非连续和大体量等特点，对大型太阳电池阵的展开过程进行动力学仿真面临着巨大的数值困难。基于共旋坐标法和无转动自由度的板壳理论，考虑柔性电池基板的几何非线性效应与电池板之间的接触碰撞，建立大变形柔性太阳电池阵的多体动力学模型。对大型的太阳电池阵的展开的动力学过程进行数值仿真，并对该过程中的复杂的动力学现象进行分析。研究结果给出了不同驱动下电池基板的响应、应力分布特征以及基板之间的碰撞规律。此项研究不仅为空间站大型太阳电池阵的设计和优化提供了参考依据，也为其它大型可展开空间结构的仿真提供了一种多体动力学分析方法。

太阳电池阵;柔性多体系统;大变形;接触碰撞;展开动力学

0 引 言

随着航天工业的发展，越来越多的学者对太阳电池阵、可展开天线等可展开结构进行多体动力学的分析。研究对象也从多刚体系统逐步拓展到了柔性多体系统。早期，周志成等[1]采用多刚体动力学的DH坐标系方法对太阳电池阵进行建模，并对其展开过程进行了多体动力学的仿真。洪嘉振等[2]基于柔性多体的单向递推组集方法建立了采用相对坐标的航天器多体系统动力学模型，对航天器中太阳电池板的展开成功地进行了仿真。刘锦阳等[3]采用单向递推组集方法对卫星太阳电池板展开过程中的碰撞力进行研究，揭示了碰撞对电池阵展开过程的影响。董富祥等[4]以星载大型可展开天线为对象，研究了索网绷紧前天线反射器桁架在轨展开的动力学过程。吴坛辉等[5]采用浮动坐标法对盘绕式可展开太阳电池阵进行了全柔性体的建模，并对展开过程进行了全局仿真。杨俊[6]采用Timoshenko梁理论对盘绕式展开桁架进行了仿真，体现了其几何非线性的特征。Liu等[7]采用绝对节点坐标法对合成孔径雷达天线进行了全局仿真，该多体动力学仿真包含25个物体共计近2000自由度，结合并行计算对该展开过程进行了仿真。田强等[8]采用自然坐标法对变拓扑卫星环形桁架天线的展开进行了仿真。张朋等[9]基于小变形假设，采用传统的Kirchhoff理论建立了展开式太阳板的动力学理论模型，对驱动展开进行了动力学分析以及对太阳板的振动进行了分析，并通过ADAMS软件进行验证。齐朝晖等[10]对周边桁架式可展开天线的展开进行了分析和控制，详细研究了电机驱动桁架展开阶段天线的展开过程，并对展开过程进行了轨迹优化。肖宁聪等[11]通过建立故障树对卫星太阳翼展开机构的可靠性进行了分析并提出了相应的改进措施。史创等[12]对双层环形可展开天线机构的构型进行了优化，并设计出一种轻量化、高刚度的可展开单元，验证了其正确性和可行性。

由于可靠性和工质比等性能出色[13]，太阳电池阵已经在国际空间站上运行了多年，如图 1所示，太阳电池阵伸展后的工作形态。但对真实的柔性基板进行展开动力学仿真的研究较少。原因首先是柔性太阳电池阵的电池基板异常纤薄，呈强烈的几何非线性特征。已有文献对刚体或者小变形的电池基板进行过仿真[5-6]，但是真实的电池基板有局部的非线性变形，采用刚体或小变形假设已不再适用。其次是层叠的电池基板必然会相互接触碰撞，如果不考虑接触碰撞会直接影响整体动力学响应，最终都将得不到正确的结果。

图1 太阳电池阵展开后形态Fig.1 The final configuration of solar arrays

文献[6-14]对太阳电池阵中间的盘绕式伸展机构进行仿真，而忽略两旁薄板的非线性变形和与之对应的接触关系。柔性太阳电池基板的动力学特性对整体动力学响应十分重要，主要体现在以下两点：首先，太阳电池基板在展开初期是折叠状态，结构会产生大量接触碰撞的现象，可能导致结构不稳定，需要对接触碰撞现象发生的区域和频率进行监测和评估；其次，太阳电池阵的基板在展开时呈大变形状态，内部可能产生较大的应力，甚至会产生撕裂，需要对大变形的过程进行动力学仿真和应力分析；除此之外，大型的太阳电池阵计算规模巨大，并且涉及大规模的接触检测问题，因此面临严峻的数值计算困难。本文考虑其几何非线性特性和基板间的接触碰撞现象，针对一种空间站大型太阳电池阵的展开过程进行多体系统动力学建模和数值仿真。揭示了太阳电池阵在展开过程中的大变形和接触过程中的动力学特性，为航天工程中空间站大型太阳电池阵的设计提供参考依据。

1 太阳电池阵的动力学建模

太阳电池阵有多种类型，大型空间站所用的主太阳电池阵一般有如图2所示的构型，中间部分是盘绕式展开机构或者铰链式展开机构[15]。底部有收纳桶，用于释放和收纳展开机构。两侧由太阳能电池基板组成阵列，电池基板之间的连接方式有普通的铰链式、柔性铰式和固定铰式等。铰链式主要用于刚性较大的电池板，不适合薄膜类型结构，容易造成局部应力过大从而撕裂电池板。而柔性铰式由于折叠处刚度不大，容易伸展，但是收拢过程不易控制。固定铰式在每两个电池板连接处固定，拉伸时会有较大的应力。收拢时由于本身的张力，更容易收拢，但会产生大变形的响应。

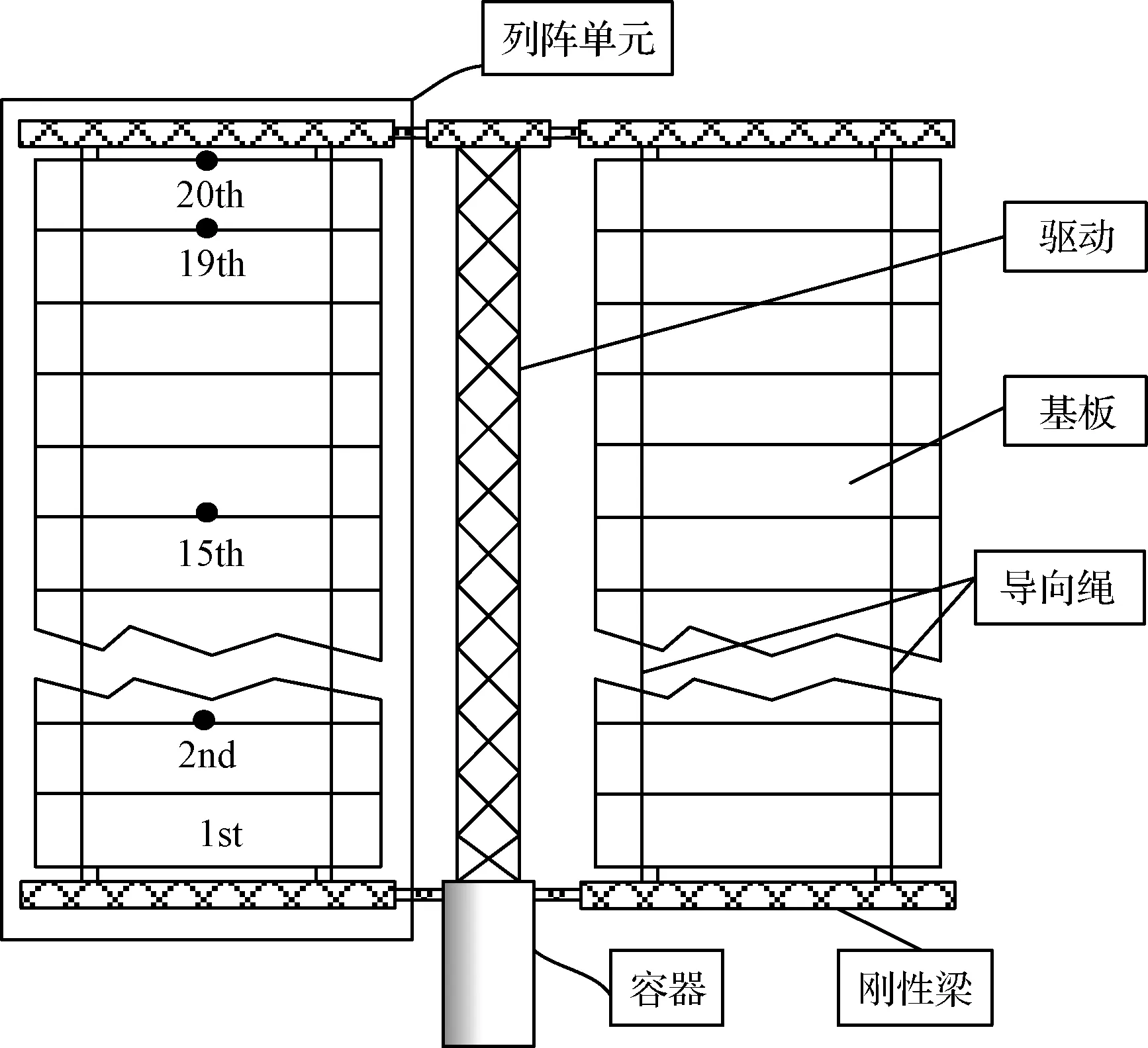
图2 太阳电池阵示意图Fig.2 The diagram of solar arrays

本文主要对固定铰式的太阳电池阵的展开进行动力学分析，即对图 2中框选的电池阵部分进行分析。着重考虑太阳电池阵展开时的大变形响应和接触碰撞现象，因此简化导向绳的作用，将其作为刚性绳索处理。为解决大变形柔性太阳电池阵展开的动力学问题，引入共旋坐标法，建立柔性板壳多体动力学模型。

1.1 大变形单个柔性基板的动力学模型

如图 3所示，任意单元都采用一个局部坐标系来描述该单元的刚体位移与转动，如初始未变形情况下局部坐标系为C0-x0y0z0，单元转动和变形之后的局部坐标系变为C-xyz。初始时刻用图中平直的三角形表示，板壳中任意一点P在初始局部坐标系C0-x0y0z0下的坐标(x0,y0,z0)。单元经过大范围的转动、平移和小应变的变形后变成图示弯曲的三角形，此时点P在局部坐标系C-xyz下的位置是(x,y,z)。点P的运动可以分为刚体运动qR和相对局部坐标变形，如下所示

(1)

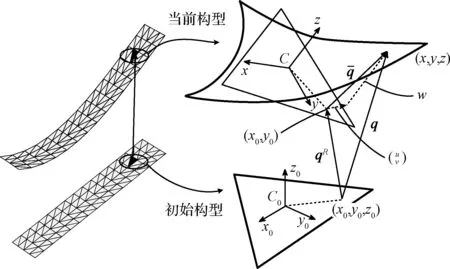
图3 变形描述Fig.3 Deformation description

如果用R=[e1e2e3]表示该单元的局部坐标系的方向余弦阵，单元在局部坐标系下的挠度可以写成

(2)

而面内的变形可以写成

(3)

对于板壳弯曲采用基于Phaal无转动自由度三角形单元[16]，而面内变形则使用常应变三角形膜单元。二者通过本文定义的共旋坐标系引入非线性效应，板壳单元的弯曲和面内变形可以通过式(2)～(3)的相对共旋系的位移得到，

(4)

内力的虚功为

δqT(fb+fm)

(5)

其中,fb是弯曲对应广义力，fm是膜内应变对应的广义力。分别对其求导数可得到内力的切线刚度阵，

(6)

其中,下标geo表示几何刚度阵，mat为线性的材料刚度矩阵。第i块电池板的内力表达式为

(7)

以及切线刚度阵为

(8)

上述方程有极为简单的几何刚度阵表达形式，因为本文无转动自由度单元的便捷性，在共旋坐标框架下，不必对切线刚度阵进行数值体积分，因此迭代效率高，计算速度快，是大规模计算的基础。

第i个电池板的惯性力可以用集中质量阵Mi来表示，外力阵用Qi来表示，于是单体的动力学方程可表示为

(9)

动力学方程(9)中，每个节点含有3个平动自由度，不含任何转动参数，避免了有限转动的非线性运算。因此方程形式简单，计算效率高。模型使用了Phaal板壳单元，具有较高的局部弯曲精度。通过使用共旋坐标法将此高精度单元拓展到大变形的板壳模型中，使此模型具有良好的精度。

1.2 大型太阳电池阵系统的多体动力学模型

本文仿真的工况为20块折叠形式的电池基板，从初始状态下展开到完全伸展状态。如图 4所示为太阳电池基板的简化力学模型和其关键尺寸。对于电池基板之间的连接本文将板间2cm连接处作固结处理。对于无转动自由度单元的固定约束，为处理方便起见，通常约束一个单元的三个节点，使之消除平移和转动，此方法与文献[17]一致。因此让图 4两条实线处和两板重叠位置的节点位置保持一致，以满足实线处两板的平移和转动相一致。因此每一对约束节点之间都有约束方程，第k个约束方程为：

(10)

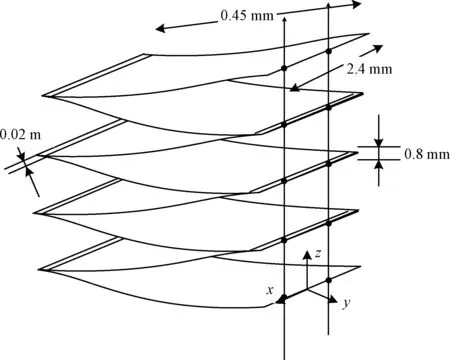
图4 太阳电池阵示意图Fig.4 The model of solar cells

在导向绳处的节点施加约束，该约束使该处节点始终沿着刚性导向绳滑动，可以通过有限元中对切线刚度阵用置大数法等对约束方程进行消除。

大变形的柔性体在变形后容易产生接触，本文使用三角形接触单元去搜索接触对和计算接触力[18]。使用层次包围盒进行接触搜索检测[19]，对单元及接触对进行并行化以提高矩阵组集的效率。其中接触力使用AugmentedLagrangian[20]形式，表达式如下

(11)

其中,k为罚因子，g为嵌入量，n为接触面法向量，X1为接触对的主接触点的在主单元上的形函数，具体形式参考文献[18]。接触力初值使用罚函数法进行计算，在主迭代步完成后对于超过嵌入阀值的接触对，进行如式(11)第2行的迭代步骤，直至收敛至没有过量嵌入，此时的接触力为真实接触力。

将式(9)～(10)进行组合，可以得到动力学方程

(12)

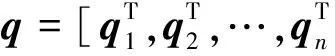
根据本文建模方法，使用C++结合OpenMP并行计算与Pardiso稀疏矩阵求解策略编制了基于无转动自由度的多体动力学求解程序，用广义-α法进行数值积分[21]。积分时引入误差估计[22]，进行步长控制已达到最优的效率。本程序具有跨平台，并行效率高，使用C++模板库特征易于扩展等特点。

2 太阳电池阵展开的仿真与分析

基于式(12)，建立总计20块电池基板的动力学方程和基板间的约束方程，对两种速度的驱动形式分别进行计算。参考了文献[5]中的伸展速度，由于不考虑中间桁架的影响，本文使用理想的伸展速度和高于理想速度一倍的两种驱动速度进行对比，在顶部电池基板的两点处分别施加两种速度驱动。如图 5所示，驱动1为正常驱动，驱动2为快速驱动。0～0.1 s为加速阶段，0.1 s之后是匀速上升阶段，实线加速度为1 m/s2，虚线加速度为2 m/s2。由于顶端位移在两种驱动下最终是一致的，因此实际驱动时间为78 s和39 s。

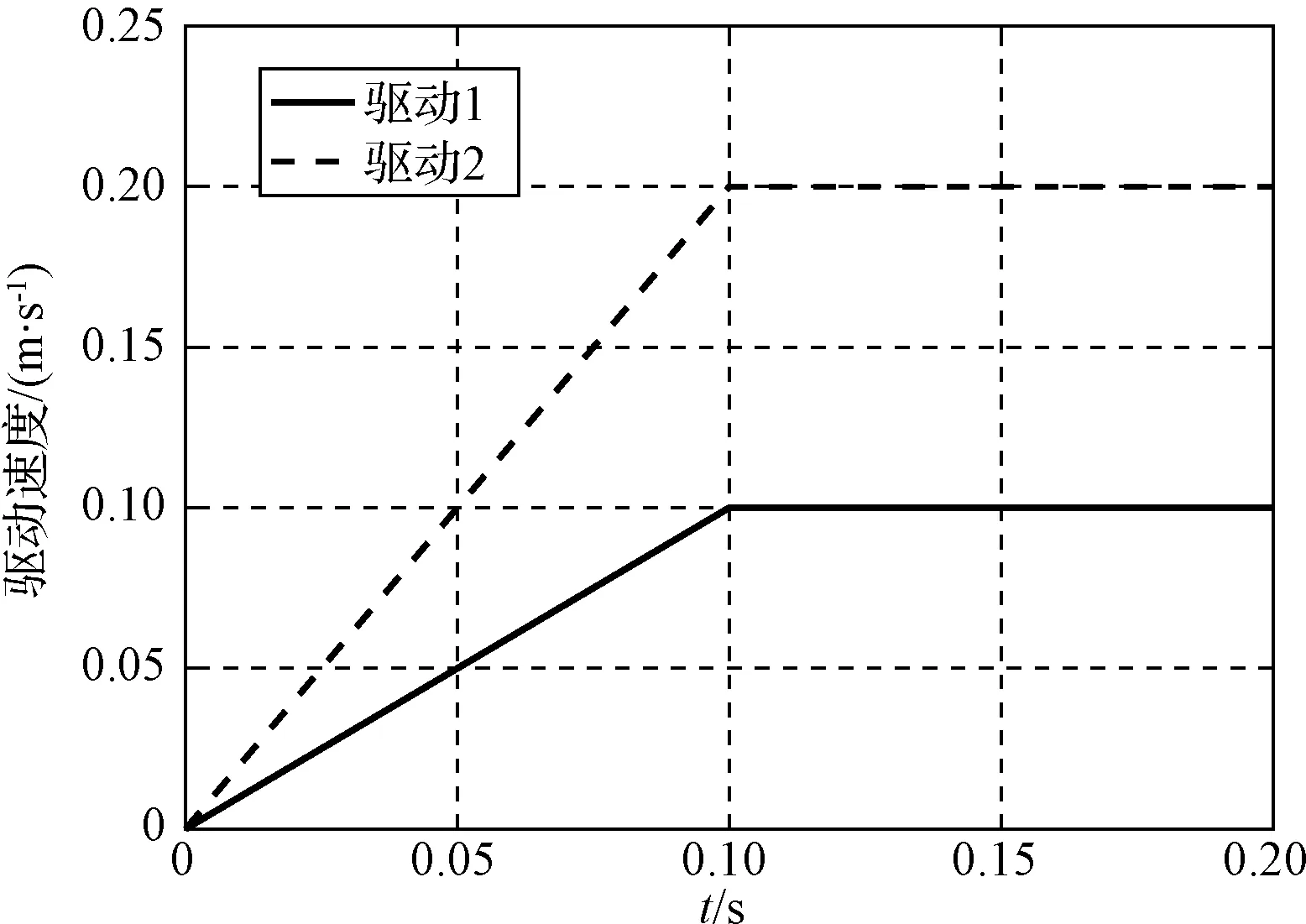
图5 顶部驱动点的速度Fig.5 Drive velocity of top point

2.1 太阳电池阵的展开仿真

该系统有27060自由度，且含有大变形和接触碰撞问题，计算复杂度较高。仿真使用计算平台为Intel Core i7-2600四核八线程处理器，内存16 GB。下面简述仿真中的各个过程。

图 6所示为以快速驱动为例的太阳电池阵展开过程。其中图6(a)～(c)阶段为伸展的初期阶段，该阶段为基板之间相互接触碰撞的阶段。图6(d)～(e)为伸展的后期，此时电池基板结构处于非线性大变形阶段。

首先在初始状态(见图6(a))，此时总体厚度大约仅0.8 mm×20=16 mm，基板间两两间隙极小，微小扰动可引起接触。当伸展至接触碰撞状态(见图6(b))，此时底部依然处于接触状态，并且由于弹性及惯性，最顶部的板向上运动，而以下的板都会往下运动，并导致下方的板互相持续接触，如图7所示。

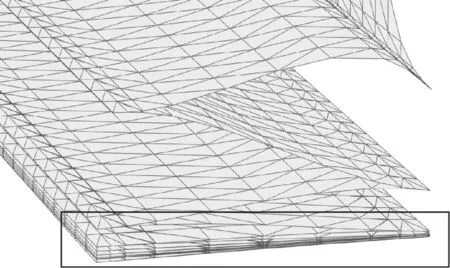
图7 太阳电池阵接触碰撞状态构型Fig.7 The contact configuration of solar cells

这个过程一直持续到半接触状态(见图6(c))，所有的基板由于最顶部的牵引都向上运动以致相互分离，仅部分板在弹性作用下偶然碰撞。继续伸展至大变形伸展状态(见图6(d))，此时基板之间由于距离伸长，没有了相互接触，转而结构本身处于几何非线性变形中，显示了其大变形的效应。伸展最终状态如图6(e)所示，电池板中间部位呈拉直状态，仅板与板约束处处于最大转动最大变形状态。此时，太阳电池阵就处于了工作状态，可进行对日定向等操作。

2.2 展开过程中各基板接触碰撞阶段分析

如第2.1节所述，太阳电池阵在展开的初始有大量碰撞现象，这个过程接触碰撞是影响系统响应的主要因素。

首先列出接触点分布情况的统计结果，计算方法为所有电池基板的相同位置处接触点进行累加，表示电池基板接触区域的总体情况。图8给出正常驱动结果，图9给出了快速驱动结果。深色表示碰撞次数较多，浅色表示碰撞次数较少。

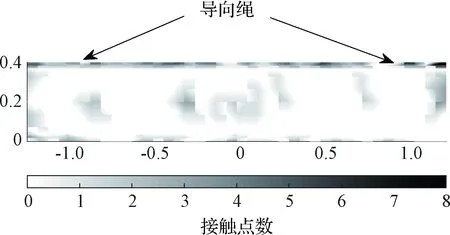
图8 电池板总体接触点分布图(正常驱动)Fig.8 The distribution of contact on the base plate (normal drive)

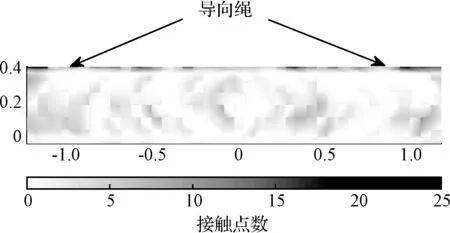
图9 电池板总体接触点分布图(快速驱动)Fig.9 The distribution of contact on the base plate (quick drive)

分析发现图8、图9有相同点：在电池板有引导绳的一边的碰撞次数明显比其余地方多，多达每个节点8次/25次碰撞，因此有引导绳的边缘处是需要设计人员特别关注的重要部位。同时在电池板内部也有一些碰撞，而这个结果在用刚体或者小变形假设的模型无法体现出来。

比较图8、图9可以得到如下结论：正常驱动形式有较少的接触机会，并且电池板内部区域的接触情况较为整齐。因为正常驱动加载后，电池板产生的变形较小，内部区域产生碰撞的概率要远小于快速驱动下的碰撞概率。

接触点数量随牵引加速度的变化而变化，可以由图10进一步分析。图中选取第10号电池基板，从初始时刻到1.5 s的碰撞数量变化图。快速驱动下不仅接触数量明显多于正常驱动，而且在碰撞持续时间上也大于正常驱动。

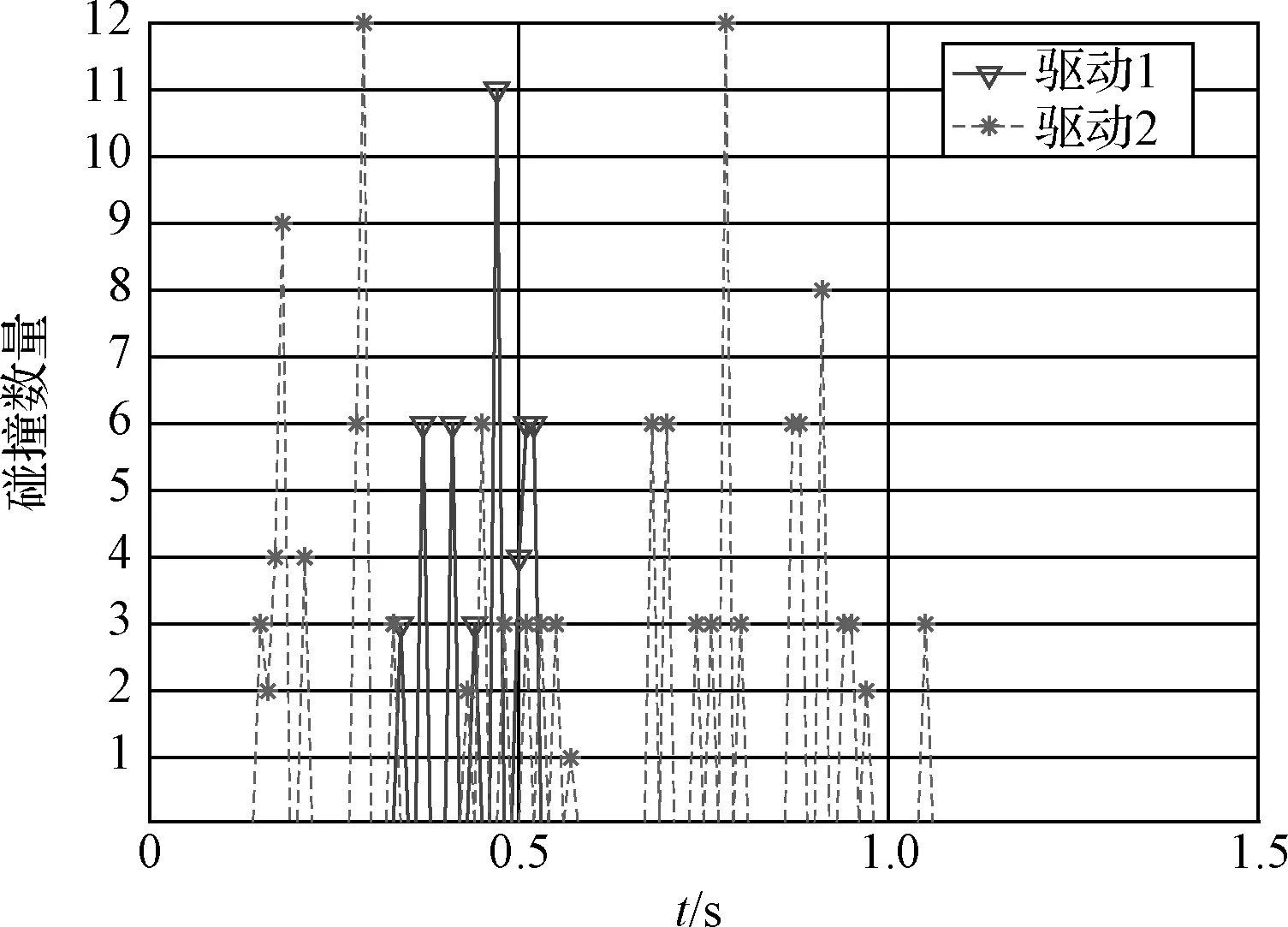
图10 第10号电池板碰撞数随时间变化图Fig.10 The number of contact of 10th plate changing with time

碰撞对于基板的Mises应力也有影响(见图11)，在展开过程中由于基板的长边边缘存在碰撞，导致了Mises应力分布并不只是在导向绳附近有剧烈变化,基板内部也存在不同程度的应力变化，但应力的最大值仍然处于驱动点处。

图11 正常驱动下展开初期Mises应力分布Fig.11 Mises stress at initial deployment period

2.3 展开过程中各基板连续运动阶段分析

对于连续运动阶段即非接触碰撞阶段，正常驱动形式和快速驱动形式表现出来的运动学特性是一致的，但局部仍有不同。因此下面对仿真结果进行分析。

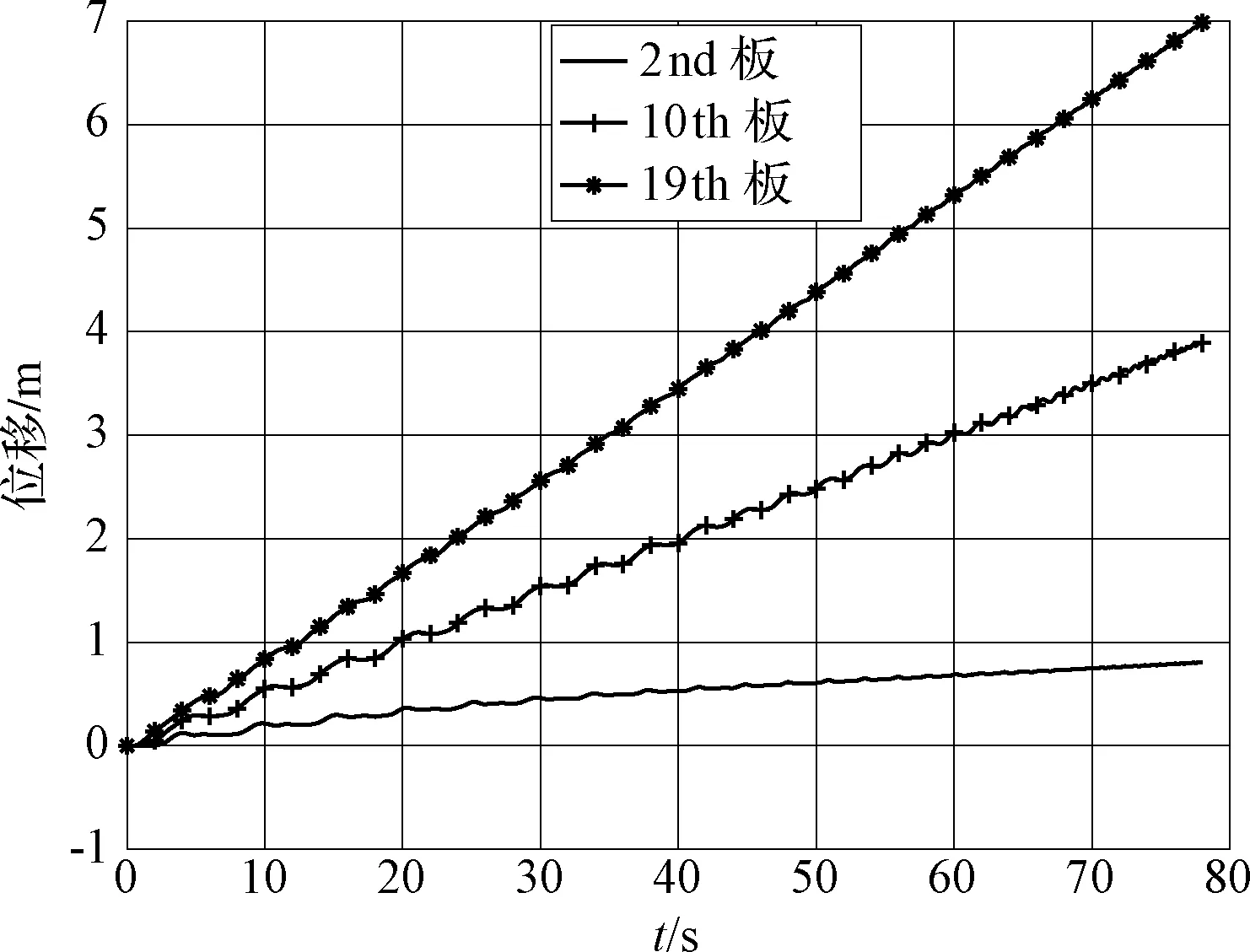
图12 第2，10，19号板的位移Fig.12 The displacements of 2nd, 10th,19th plate

从中选取底部、中间和顶端三个代表性的电池基板的上沿中点(即图2中标示点)为观察点。从图 12可以看出,三个点在初始阶段稍有波动，说明初始时刻有接触碰撞产生。结合图 13所示的速度曲线图，在0时刻附近有较剧烈波动，属于接触碰撞的速度突变。而在展开过程中，各基板长期处于稳定的振动，周期性较明显，这也说明了该形式的板间约束形式具有较好的稳定性。伸展的末期，如图 13所示，此刻基板观察点剧烈高频振动。因为在伸展的末期，各板都处于张紧状态,此时将多体系统看作一个整体，固有频率比松弛状态提高，因此体现在速度上会有剧烈振动。

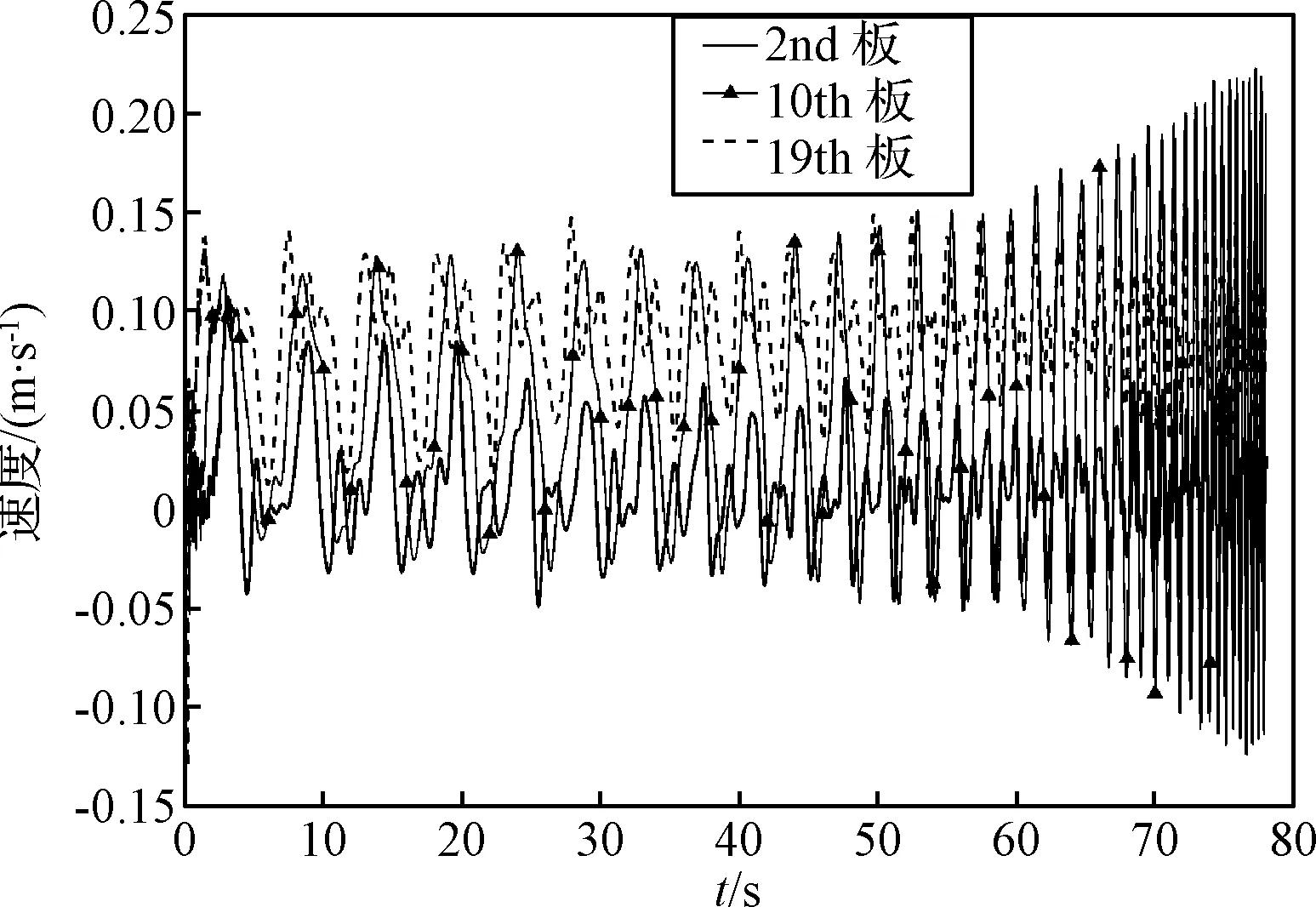
图13 第2，10，19号板的速度Fig.13 The velocity of 2nd,10th,19th plate

观察图 13发现位于中间(10号板)的电池基板的振幅最大，图中速度曲线最大值和19号板一致，而最低值与2号板一致，说明中间的电池板所受约束作用较弱，自由振动明显。

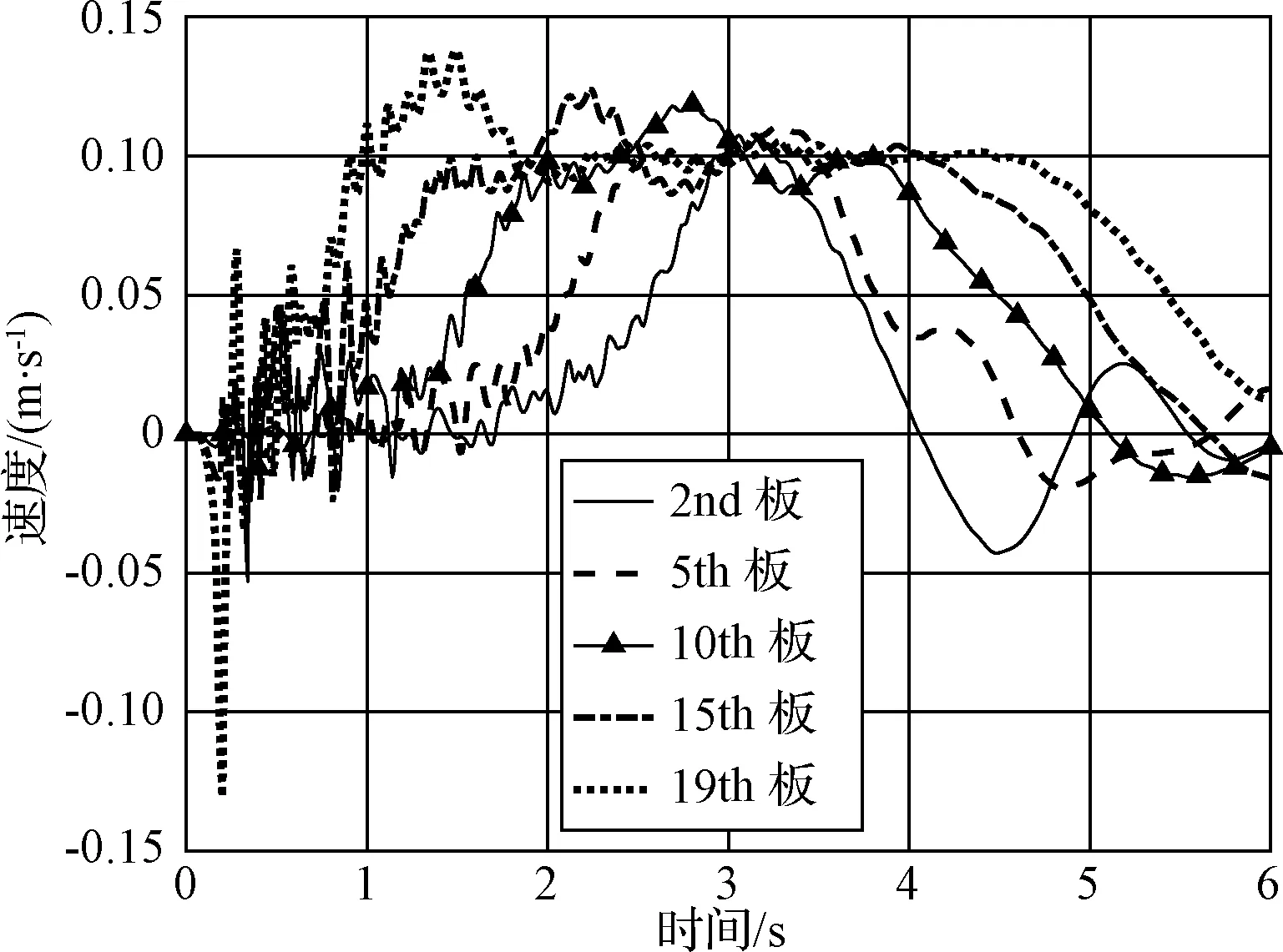
图14 第2，5，10，15，19号板的速度图Fig.14 The velocity of 2nd,5th,10th,15th,19th plate

图14画出了第2、5、10、15、19号太阳电池基板的前6 s的速度响应。图中每块电池板的速度极值点从顶部到底部是依次产生的，具有严格的次序。证实了太阳电池基板中应力传播从最顶部的驱动处依次传播至最底部的电池板。

图15 快速驱动和正常驱动的伸展时刻对比Fig.15 Configuration comparison between quick and normal drive

图15展示了不同速度的驱动下形成不一样的构型。其中快速驱动会形成非均匀的电池基板排列，从而加大了接触碰撞的可能性。而慢速驱动则形成了规律并均匀的电池基板排列，因此减少了碰撞的可能性。同时图15的左图也印证了图14中速度极值出现的依次顺序。图中颜色表示电池基板面高斯曲率的数值，表征了其弯曲应变的大小。板间的张角直接体现了弯曲变形大小。快速驱动的曲率最大值在上部的电池板，而慢速驱动的曲率最大值在下部的电池板。

分析可知在伸展的末期，结构存储了最大的应变能。由于弯曲应变与电池基板的厚度相关，而电池基板的厚度极小(0.8 mm)，因此与曲率相关的应变很小，所以在此考虑最终形态的面内的膜应力。

图16 第19和20号电池板的Mises 应力图Fig.16 Mises stress of 19th and 20th plate

图16为最终形态的最上部两块电池板的Mises 应力图，可以看出仍然在驱动点处有最大的应力，最大值约为30 kPa，量级上远小于屈服极限，因此相对安全。结合图11和图16，发现驱动点处的应力始终处于最大值，仍然需要设计人员注意。而板间连接处由于连接点数量大，因此应力平均分布，不会产生如驱动点处的应力集中，因此此种连接安全可靠。

3 结 论

本文基于共旋坐标法，建立了空间站的大型太阳电池阵的展开的多体动力学模型，考虑了其大变形效应和接触碰撞现象，针对一个总自由度为27060的大规模太阳电池阵系统，成功地仿真了展开过程中的各种现象，使大体量大变形的太阳电池阵展开动力学仿真成为现实。

大型太阳电池阵动力学展开过程有以下特征，可供太阳电池阵的总体设计人员参考。首先，太阳电池阵的展开过程中处于中间部位的电池板有最大的振动幅度，而最大应力则出现在驱动点处，此处需要特别关心。电池基板按照固定铰连接不会在基板之间产生应力集中，该处应力值相对较小。其次，展开初期的电池基板上带导向绳的一侧存在大量的接触。因此该边缘处应当予以关注。最后，通过对比不同的驱动速度，发现驱动越快，接触碰撞的频率随之提高，是因为快速驱动速度会导致不均匀的电池基板分布，而慢速驱动下电池板分布是均匀有序的。因此大型太阳电池阵的展开尽可能采用较慢的驱动速度。

[1] 周志成, 曲广吉. 航天器太阳阵多体展开的动力学分析[J]. 力学与实践, 1990(6): 53-57.[Zhou Zhi-cheng, Qu Guang-ji. Multibody dynamics analysis for the deployment of solar array in the spacecraft[J]. Mechanics in Engineering, 1990(6): 53-57.]

[2] 洪嘉振, 潘振宽. 柔性多体航天器动力学[J]. 宇航学报, 1992, 13(4): 59-68.[Hong Jia-zhen, Pan Zhen-kuan. Dynamics of flexible multibody spacecrafts[J]. Journal of Astronautics, 1992, 13(4): 59-68.]

[3] 刘锦阳, 洪嘉振. 卫星太阳电池阵在板展开阶段得撞击特性研究[J]. 空间科学学报, 1999, 20(1): 61-67.[Liu Jin-yang, Hong Jia-zhen. Contact-impact of solar battery during the deployment of the plates[J]. Chinese Journal of Space Science, 1999, 20(1): 61-67.]

[4] 董富祥, 周志成, 曲广吉. 星载大型天线反射器桁架展开动力学建模仿真[J]. 航天器工程, 2012, 21(4): 26-31.[Dong Fu-xiang, Zhou Zhi-cheng, Qu Guang-ji. Deployment dynamics modeling and simulation of satellite large antenna reflector truss[J]. Spacecraft Engineering, 2012, 21(4): 26-31.]

[5] 吴坛辉, 史加贝, 洪嘉振,等. 国际空间站伸展式柔性翼展开动力学仿真[C]. 第七届全国多体系统动力学暨第二届全国航天动力学与控制学术会议, 福州,中国,2011年11月4-6日.[Wu Tan-hui, Shi Jia-bei, Hong Jia-zhen, et al. Dynamics simulation for the flexible solar array in the international space station[C]. The 7th National Symposium on Multi-body System Dynamics and the 2nd National Conference on Aerospace Dynamics and Control Conference, Fuzhou, China, Nov 4-6, 2011.]

[6] 杨俊. 大型太阳翼盘绕式展开机构多体动力学研究[D]. 北京: 清华大学, 2013.[Yang Jun. Study on the multibody dynamics of large scaled coiled deployment mechanism[D]. Beijing: Tsinghua University, 2013.]

[7] Liu C, Tian Q, Hu H. Dynamics of a large scale rigid-flexible multibody system composed of composite laminated plates[J]. Multibody System Dynamics, 2011, 26(3): 283-305.

[8] 田强, 刘铖, 刘丽坤,等. 变拓扑卫星环形桁架天线展开动力学研究[J]. 系统仿真学报, 2013, 25(6): 1351-1358.[Tian Qiang, Liu Cheng, Liu Li-kun, et al. Deployable dynamics research on variable topology satellite hoop truss antenna[J]. Journal of System Simulation, 2013, 25(6): 1351-1358.]

[9] 张朋，高海波，邓宗全，等. 展开式太阳板的动力学分析[J]. 宇航学报，2009，30(4):1359-1364.[Zhang Peng, Gao Hai-bo, Deng Zong-quan, et al. Dynamics analysis of deployable solar panel[J]. Journal of Astronautics, 2009，30(4):1359-1364.]

[10] 齐朝晖，常进宫，王刚. 周边桁架式可展开天线展开分析与控制[J]. 宇航学报，2014，35(1):61-68.[Qi Zhao-hui, Chang Jin-gong, Wang gang. Analysis and control of deployment process for hoop truss deployable antenna[J]. Journal of Astronautics, 2014，35(1):61-68.]

[11] 肖宁聪，李彦锋，黄洪钟. 卫星太阳翼展开机构的可靠性分析方法研究[J]. 宇航学报，2009，30(4):1697-1703.[Xiao Ning-cong, Li Yan-feng, Huang Hong-zhong. Reliability analysis method of deployment mechanism of a satellite solar arrays[J]. Journal of Astronautics, 2009，30(4):1697-1703.]

[12] 史创，郭宏伟，刘荣强，等. 双层环形可展开天线机构构型优选及结构设计[J]. 宇航学报，2016，37(7):869-878.[Shi Chuang, Guo Hong-wei, Liu Rong-qiang, et al. Configuration optimization and structure design of the double-layer hoop deployable antenna mechanism[J]. Journal of Astronautics, 2016，37(7):869-878.]

[13] 谢宗武, 宫钇成, 史士财,等. 空间太阳能电池阵列技术综述[J]. 宇航学报, 2014, 35(5): 491-498.[Xie Zong-wu, Gong Yi-cheng, Shi Shi-cai, et al. A survey of the space solar array technique[J]. Journal of Astronautics, 2014, 35(5): 491-498.]

[14] 张淑杰, 李瑞祥, 丁同才. 盘绕式杆状展开机构的设计与力学分析[J]. 力学季刊, 2006, 27(2): 341-347.[Zhang Shu-jie, Li Rui-xiang, Ding Tong-cai. Design and mechanical analysis of coilable lattice mast[J]. Chinese Quarterly of Mechanics, 2006, 27(2): 341-347.]

[15] 刘志全, 黎彪, 程刚. 桁架式空间可展开支撑臂[J]. 中国空间技术科学, 2011(2): 32-38.[Liu Zhi-quan, Li Biao, Cheng Gang. Review of deployable-truss masts for space application[J]. Chinese Space Science and Technology, 2011(2): 32-38.]

[16] Phaal R, Calladine C R. A simple class of finite elements for plate and shell problems. I: Elements for beams and thin flat plates[J]. International Journal for Numerical Methods in Engineering, 1992, 35(5): 955-977.

[17] Linhard J, Wüchner R, Bletzinger K-U. ‘Upgrading’ membranes to shells—The CEG rotation free shell element and its application in structural analysis[J]. Finite Elements in Analysis and Design, 2007, 44(1-2): 63-74.

[18] Wriggers P. Computational contact mechanics[M]. Berlin, Gemany: Springer, 2006.

[19] Bergen G V D. Efficient collision detection of complex deformable models using AABB trees[J]. Journal of Graphics Tools, 1997, 2(4): 1-13.

[20] Hirmand M, Vahab M, Khoei A R. An augmented Lagrangian contact formulation for frictional discontinuities with the extended finite element method[J]. Finite Elements in Analysis and Design, 2015, 107: 28-43.

[21] Arnold M, Brüls O. Convergence of the generalized-α scheme for constrained mechanical systems[J]. Multibody System Dynamics, 2007, 18(2): 185-202.

[22] Rang J. Adaptive timestep control for the generalised-alpha method[C]. VI International Conference on Adaptive Modeling and Simulation, Portugal, June 3-5, 2013.

通信地址：上海交通大学木兰船建大楼A908(200240)

电话：(021)34204413

E-mail:sjbnust@163.com

刘铸永(1979-)，男，博士，讲师，主要从事多体系统动力学和航天器动力学研究。本文通信作者。

通信地址：上海交通大学木兰船建大楼A931(200240)

电话：(021)34206496

E-mail:zhuyongliu@sjtu.edu.cn

Multi-Body Dynamics Analysis of Deployment of Solar Arrayswith Large Deformation

SHI Jia-bei, LIU Zhu-yong, HONG Jia-zhen

(School of Naval Architecture, Ocean and Civil Engineering,Shanghai Jiao Tong University, Shanghai 200240, China)

Owing to the large deformation, non-continuity and contact/impact, the simulation for the deployment of the large scaled solar arrays is faced with great numerical difficulty. In this paper, based on the co-rotational formulation and the plate/shell theory without rotation, a multibody dynamic model of a flexible solar array is established by considering the geometrically nonlinear effect of flexible battery cell and the contact/impact between the battery plates. Then the numerical simulation of the deployment process of the large solar cell array is carried out, and the complex dynamic phenomena in the development process are analyzed. The results given by this study show the features of the response, the stress distribution and the regular pattern of the contact between the base plates. This work can be referred to design and optimize the large scaled solar arrays in the space station, and it can be easily extended to the simulation for other large scaled space structures.

Solar array; Flexible multibody system; Large deformation; Contact/impact; Deployment dynamics

2017- 03-23;

2017- 05-25

国家自然科学基金(11772188,11132007)

V414.4

A

1000-1328(2017)08-0789-08

10.3873/j.issn.1000-1328.2017.08.002

史加贝(1987-)，男，博士生，主要从事大变形多体动力学仿真与接触碰撞计算。