多参数空间的非线性非定常气动力降阶模型

陈志强，赵永辉

(南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016)

多参数空间的非线性非定常气动力降阶模型

陈志强，赵永辉

(南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016)

基于线性卷积和修正因子，发展了一种多参数空间的非线性、非定常气动力降阶模型(ROM)，从而高效地获得准确的非定常气动力。首先，基于阶跃响应的卷积构建线性降阶模型；然后应用拉丁超立方抽样得到参数空间内的抽样点，分别计算各抽样点处的修正因子；利用Kriging插值得到整个参数空间内的修正因子，从而得到参数空间内的修正降阶模型。以Isogai机翼为研究对象，考虑马赫数、俯仰振幅、沉浮振幅和减缩频率的变化对降阶模型精度的影响；最后将模型降阶与模型结构方程耦合，进行气动弹性分析并预测颤振边界，由此论证了该降阶模型的有效性。

修正因子；拉丁超立方抽样；Krigin插值；非线性非定常气动力；降阶模型(ROM)

0 引 言

非定常气动力是气动伺服弹性系统的重要组成部分之一，其建模的好坏直接影响到整个气动伺服弹性分析与综合的成败。随着计算方法和计算机性能的提高，产生了各种基于计算流体力学(Computation fluid dynamics,CFD)的非定常气动力计算方法。这些方法通常需要复杂的气动网格，在结构与气动之间反复迭代计算，消耗巨大的计算时间，并且非定常气动力的数据量大，因此采用这些方法进行气动伺服弹性分析与综合非常困难。基于CFD的模型降阶(Reduced-order model,ROM)方法为非定常气动力的计算提供了一个有效的手段。近些年来，各种非定常流场ROM技术得到了很大的发展，文献[1]全面系统地介绍了非定常流场ROM的国内外研究进展，对其发展趋势和应用前景进行了展望，并指出自适应鲁棒ROM是下一代ROM技术的发展方向。

在线性系统中，用CFD计算得到单位阶跃或脉冲激励的系统响应，然后应用Duhamel原理得出的卷积积分方式可以得到任意运动下的响应。Volterra级数是通过卷积增加高阶非线性项进行非线性模拟[2]，已经有很多文献研究其在非定常气动力上的应用。文献[3-5]系统研究了基于CFD/CSD耦合求解器的Volterra/ROM建模方法，发展了基于Volterra/ROM的气动弹性主动控制律设计方法。为了考虑系统高频响应，文献[6]提出了离散气动力脉冲响应的概念，发展了基于CFD模型求取Volerra核的辨识方法，并成功用于亚声速和跨声速直机翼气动分析。文献[7-8]发现用CFD求解器辨识结构脉冲产生的非定常气动力有时很不稳定，而采用阶跃响应计算Volterra核比用脉冲响应稳定性有很大提高；并且一阶核就能描述大部分气动非线性，增加高阶核对提高精度效果并不是特别明显。

航空航天飞行器的飞行包线一般都包含多个马赫数区间，例如高超声速飞行器[9]，从起飞经过亚声速、跨声速、超声速，继而达到高超声速巡航。在每一个马赫数区间，都要进行相应的气动力建模。然而，在进行控制仿真时更希望用一个气动力模型尽可能地涵盖多个马赫数区间；这样不仅可以避免转换模型时计算时间的增加和可能导致的误差，而且消除了不同气动力模型的边界条件不匹配；因此，大大提高了整个仿真的效率。

正如前面所讲，希望建立能适用大范围马赫数(或者其它飞行参数)的ROM，而不是只在很小的马赫数区间内有效。文献[10]从风洞试验提取数据，用Volterra核得到在多个不同飞行条件下的状态空间系统，并且可以预测除测试的飞行条件以外的气动力。文献[11]运用插值方法由子模型的Volterra核得到全局的核，分段插值的方法应用到各个子模型的转换，从而得到适用较广泛的飞行参数的ROM。文献[12]运用非线性变参数方法拓展前述Volterra模型，能够在多个飞行参数范围捕捉强非线性现象。文献[13]在线性降阶方法的基础上引入修正因子，使其在一定模态振幅和马赫数范围内有效，并将此方法应用到高超声速飞行器的非定常气动力预测。

采用阶跃响应辨识Volterra核的限制在于阶跃输入的幅值不能过大，否则可能导致CFD程序出现数值问题。引入修正因子，从而避免该问题。本文建立一个结合修正因子的线性卷积的非定常气动力ROM，在参数空间内计算修正因子，从而使ROM在这个参数空间内有效。本文将该方法应用到跨声速非定常气动力的预测，以两自由度翼型为例；通过与直接CFD计算结果对比，证明ROM的有效性，并发展一个误差指标用于评估ROM的精度；最后，把ROM与模型结构方程耦合，进行气动弹性分析并预测颤振边界。

1 非定常气动力的降阶模型

图1表示构建非定常气动力ROM的整体流程。首先，由CFD计算得到模型的阶跃响应，利用卷积积分得到模型在任意振动下的响应，即为未修正的线性ROM响应；然后，计算抽样点处的修正因子，利用Kriging插值得到参数空间内的修正因子的值；最后，引入修正因子到线性ROM得到修正后的非线性ROM。ROM的输入是模型的模态振型和模态振幅，输出是非定常的时间精度的气动力系数。

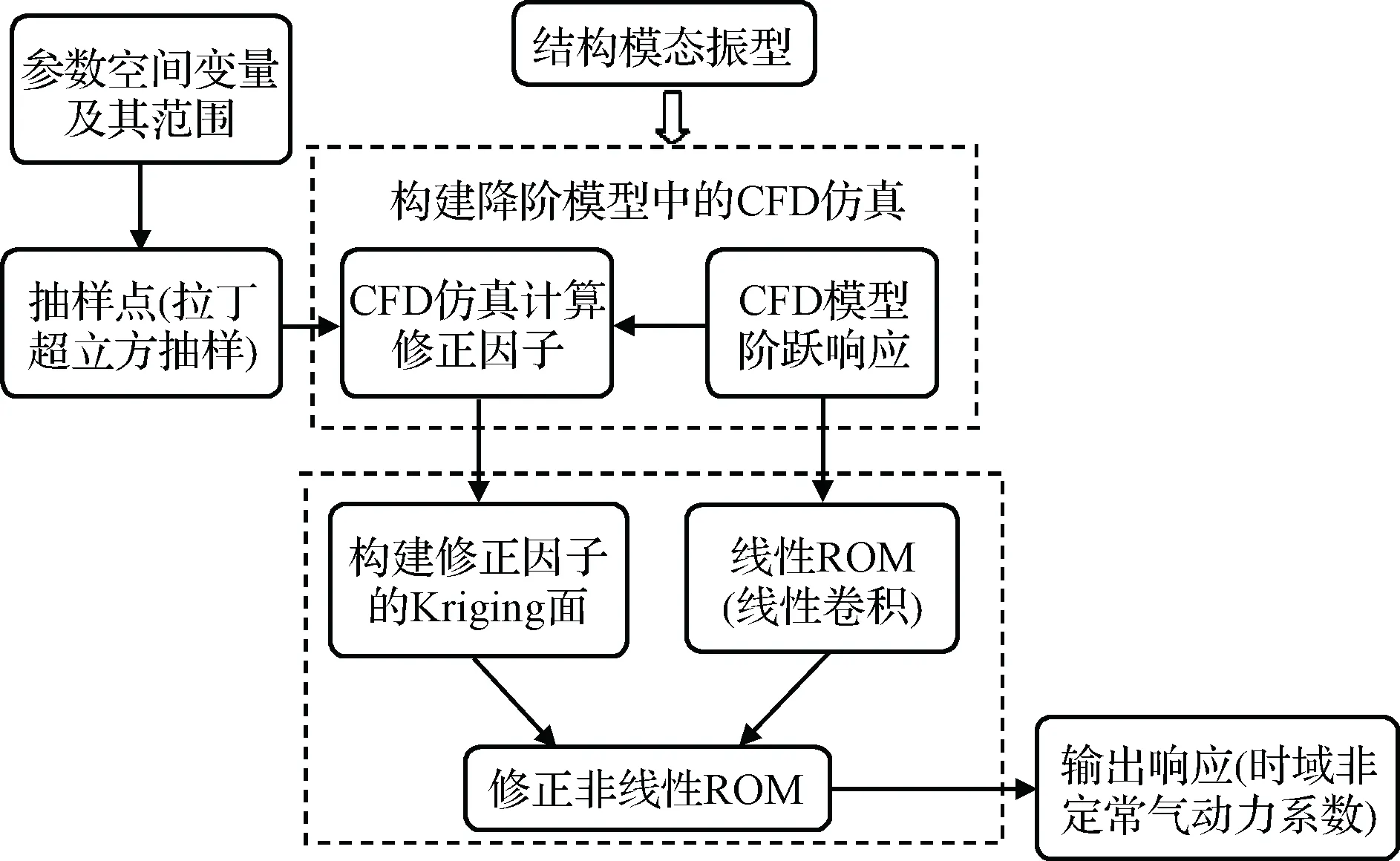
图1 非定常气动力ROM流程图Fig.1 Schematic of ROM for unsteady aerodynamics

1.1 线性卷积

如果知道系统对单位阶跃激励和单位脉冲激励的响应，就可以得到线性系统对任意输入的响应。文献[7]指出利用阶跃响应可以得到更佳的结果且容易用于CFD计算，并且不太容易产生数值问题，所以选用阶跃输入。连续时间域，系统对任意输入f(t)的响应y(t):

(1)

应用到CFD时需转化为离散格式:

u[n-1])H[n-k]

(2)

经过线性卷积得到的结果作为线性ROM的响应，即为yconv。

另外需要指出的是在本文研究中，系统的输入为模态位移，则：模态位移阶跃输入

(3)

式中:A0是模态位移的幅值；然后要将CFD的阶跃响应正则化，即为式(2)中的H[n-k]。

在进行CFD阶跃响应计算时，需要确定时间步长和模态阶跃幅值，在此遵守以下原则：1)时间步长要选择足够小以达到足够的分辨率的响应，从而保证每个周期内有足够的时间步；2)必须控制网格的变形幅值和变形速度，保证CFD程序不出现数值

问题，所以根据时间步长，确定合适模态阶跃输入幅值；3)基于线性扰动的假设，网格的变形幅值和变形速度应该保持足够小。

1.2 修正因子

线性降阶方法的局限性在于它只适用于小振幅情形，若实际的系统具有较强的非线性效应，线性模型会有较大的误差。为了扩大降阶模型的适用范围，本文引入修正因子fc，其定义为线性与非线性响应的比值关系

(4)

首先确定输入参数值，比如马赫数、模态振幅等；然后将相应振幅的阶跃激励同时施加在相应的模态上，CFD计算得到的收敛响应值即为ynonlin；对于较大幅值的情况，防止CFD程序出现数值问题，逐步增加幅值达到最终值，得到稳定的响应值即为ynonlin；最后分别在各个模态上施加单位阶跃激励得到收敛响应值，再乘上相应的模态振幅，各个模态的响应值相加的和即为ylin。δ为引入的偏移量，避免出现数值问题。修正因子计算过程的说明如图2～3所示。

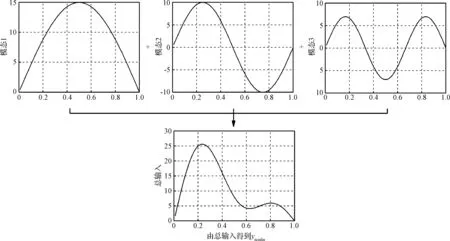
图2 计算ynonlin的示意图Fig.2 Schematic for the calculation of ynonlin

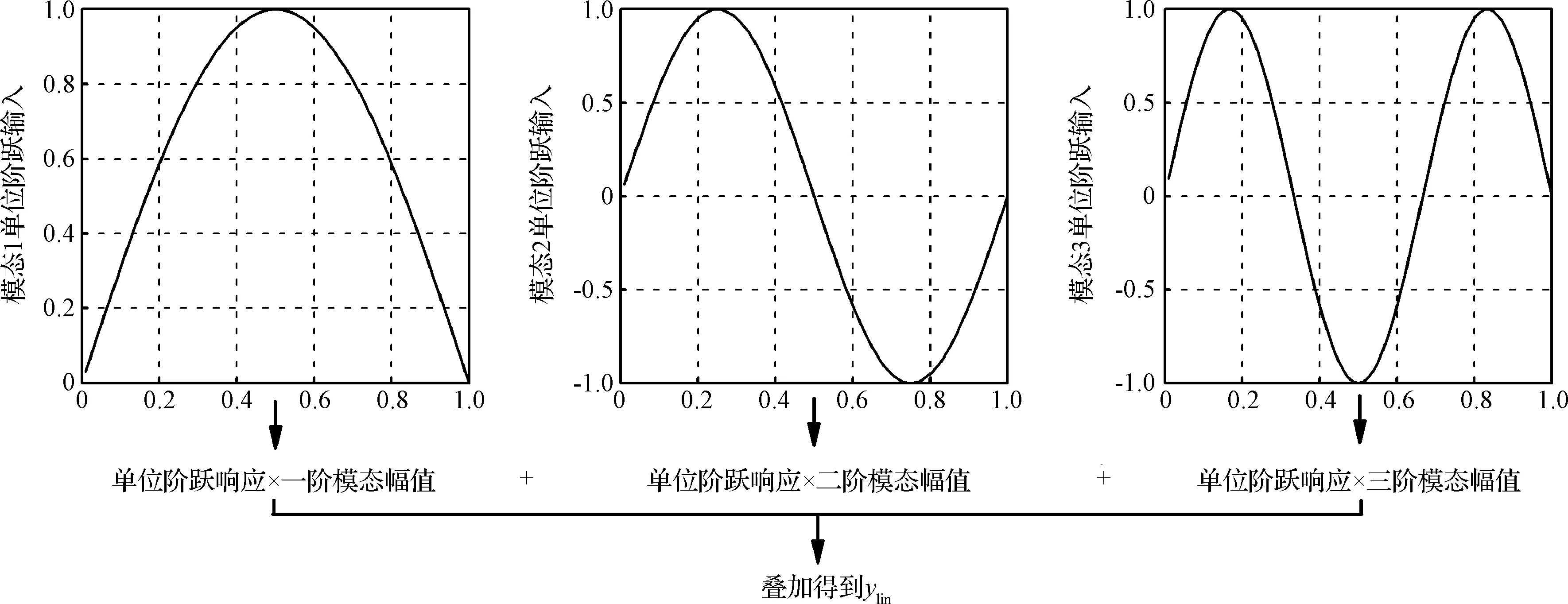
图3 计算ylin的示意图Fig.3 Schematic for the calculation of ylin

得到修正因子后，修正线性ROM的响应值yconv，修正后的响应值ycorr可表示为：

ycorr=fc(yconv+δ)-δ

(5)

1.3 拉丁超立方抽样

为了构建准确的修正因子Kriging面，必须在参数空间内选择足够的抽样点，本文应用拉丁超立方抽样选取参数空间内合适的抽样点。

基于Maximin准则的逐次局部枚举拉丁超立方试验设计方法[14](Successive local enumeration, SLE)的采样过程是一个简单的局部优化过程，目标为待选定的样本点与已生成的样本点之间的最小距离最大化。与其它现有拉丁超立方采样算法最大的不同在于，其它算法采样过程中有全局目标函数，采样过程繁琐复杂，由于优化过程的不确定性且存在着鲁棒性不高的问题，而SLE方法采样过程中的目标函数为局部的最小距离最大化，具有更高的空间均匀性和投影均匀性。

1.4 Kriging插值

Kriging模型是1951年由Danic Krige提出的一种估计方差最小的无偏估计模型，它通过相关函数的作用，具有局部估计的特点，对非线性模型有很好的逼近能力。文献[15]用Kriging模型近似估计确定的计算模型，复杂形式的Kriging模型能更准确更容易地估计计算模型。

假定在一个N维的设计空间取M个样本点x(1),x(2),…,x(M)，y=[fc1,fc2,…,fcM]是这些抽样点处的修正因子值，在Kriging模型中，需要插值的未知函数Φ(x)表示为如下形式：

(6)

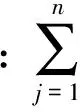
(7)

式中:RM×M为相关矩阵，元素Rij=R(x(i),x(j))。

(8)

式中:N表示x的维数，pk是需要确定的相关模型参数。

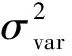
(9)

式中:F是维数为M×n的矩阵，第i行表示对应第i个采样点的n个回归模型。

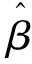
(10)

式中:

r(x)=[R(x,x(1))R(x,x(2)) …R(x,x(M))]T

(11)

1.5 利用修正因子修正ROM

修正因子的Kriging面构建完成以后，即可引入修正因子修正线性ROM。在任一时间步上，已知相应的马赫数和模态振幅，可由修正因子的Kriging面中获得对应的修正因子fc，代入式(5)即为修正后的响应值。ROM计算中的每一个时间步都要重复上述过程。

1.6 误差分析

在此，定义误差参数用于量化ROM的精度。均方根误差(Lerror)定义为：

(12)

式中:yROM,i表示第i时间步上ROM的响应值，yCFD,i表示第i时间步上CFD的响应值，分母表示在整个CFD响应值中最大值与最小值的差。

2 算例与分析

2.1 模型描述

本节以Isogai机翼模型为研究对象，分别研究ROM在参数空间内的精度和跨声速颤振边界预测，从而论证非线性ROM的有效性。图4为Isogai机翼的两自由度力学模型，该翼段模型采用NACA64A010翼型为气动外形，其气动网格如图5所示。

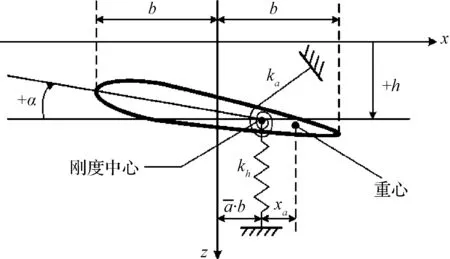
图4 Isogai机翼的两自由度力学模型Fig.4 Two-degree-of-freedom model of Isogai wing model

图4中，xα是重心到刚心的距离，b是半弦长，rα是机翼对刚心的回转半径，kh和kα分别是沉浮刚度和扭转刚度。

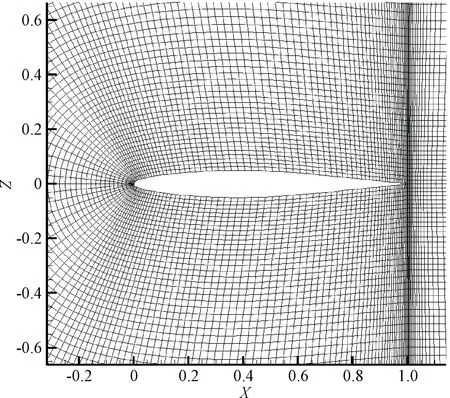
图5 NACA64A010翼型的气动网格Fig.5 Computational grids for a NACA64A010 airfoil

对于二元翼段，其气动弹性方程如下：

(13)

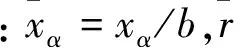
(14)

式中:ρ∞为无穷远处来流密度，V∞为无穷远处来流速度，cR为平均气动力弦长。

(15)

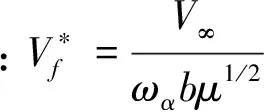
2.2 修正因子的计算

对于流场的CFD计算，采用半离散有限体积法求解基于Spalart-Allmaras湍流模型的可压雷诺平均纳维-斯托克斯控制方程，雷诺数为4×106。本文研究翼型在零攻角下的俯仰和沉浮两种振动模态，无量纲的时间步长为0.6。

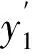
2.3 构建修正因子的Kriging面

在此，考虑的参数有：马赫数Ma，俯仰振幅d1，沉浮振幅d2，选取的范围见表1。

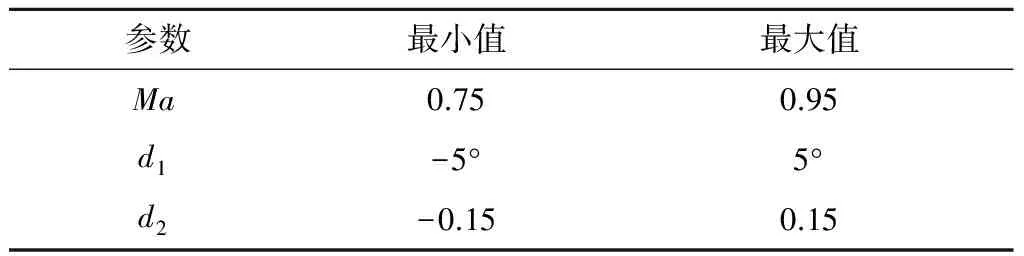
表1 参数取值范围

因为翼型NACA64A010是对称翼型，负的幅值下的升力系数和力矩系数与相应正的幅值下的升力系数和力矩系数互成相反数，所以可大幅减少CFD的计算量。应用SLE在参数空间内得到107个样本点用于构建修正因子的Krigin面。

2.4 马赫数测试

为了测试不同马赫数对ROM精度的影响，保持模态振幅d1=3°,d2=0.1和振动频率ωh=ωα=100 rad/s不变，考察马赫数区间0.75～0.95中模型的误差。另外，选取4个马赫数用于构建ROM，即Mastep=0.8,0.85,0.9,0.95；并且在相应马赫数下的阶跃响应用于计算yconv。在此，马赫数区间内选取10个点用于分析，测试结果如图6～7所示。由图6～7可知，升力系数和力矩系数的误差都比较小，在4%以内，并且整体趋势相似，升力系数和力矩系数对Mastep较为敏感，当仿真马赫数Masim与Mastep越接近时，误差也相对越小。

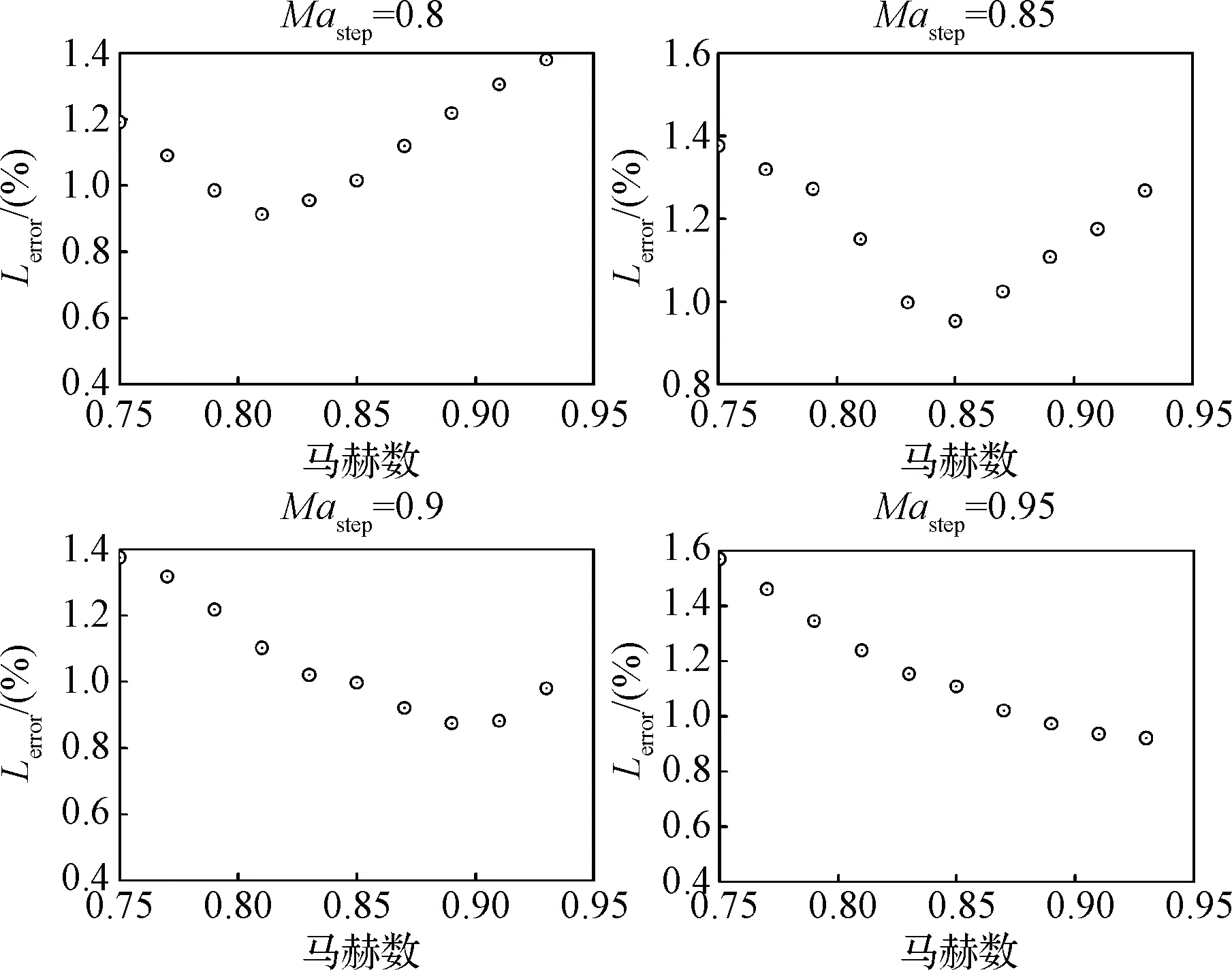
图6 升力系数误差Fig.6 Errors of lift coefficient

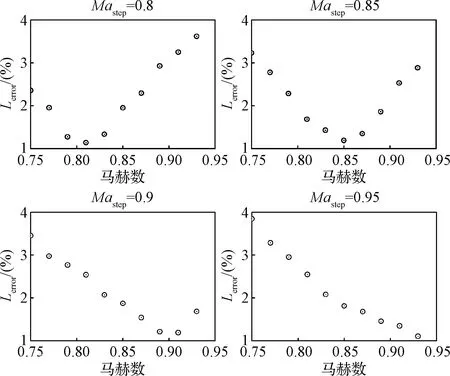
图7 力矩系数误差Fig.7 Errors of moment coefficient

2.5 振幅测试

为了测试两阶模态振幅的增加对ROM精度的影响，现保持马赫数Masim=0.85与减缩频率k=0.172不变，考察不同振幅下ROM的误差，并对比修正后的降阶模型与未修正的降阶模型的误差。用于计算ylin和yconv的马赫数Mastep=0.85。首先测试俯仰振幅d1，令沉浮振幅d2=0，升力系数和力矩系数的误差如图8所示；然后令俯仰振幅d1=0，测试沉浮振幅d2，升力系数和力矩系数的误差如图9所示。对比结果显示，修正后的ROM的误差在振幅参数范围内都很小，并保持基本一致，但未修正的ROM的误差随着幅值的增大而快速增加；说明修正因子的加入对ROM的修正效果非常明显。

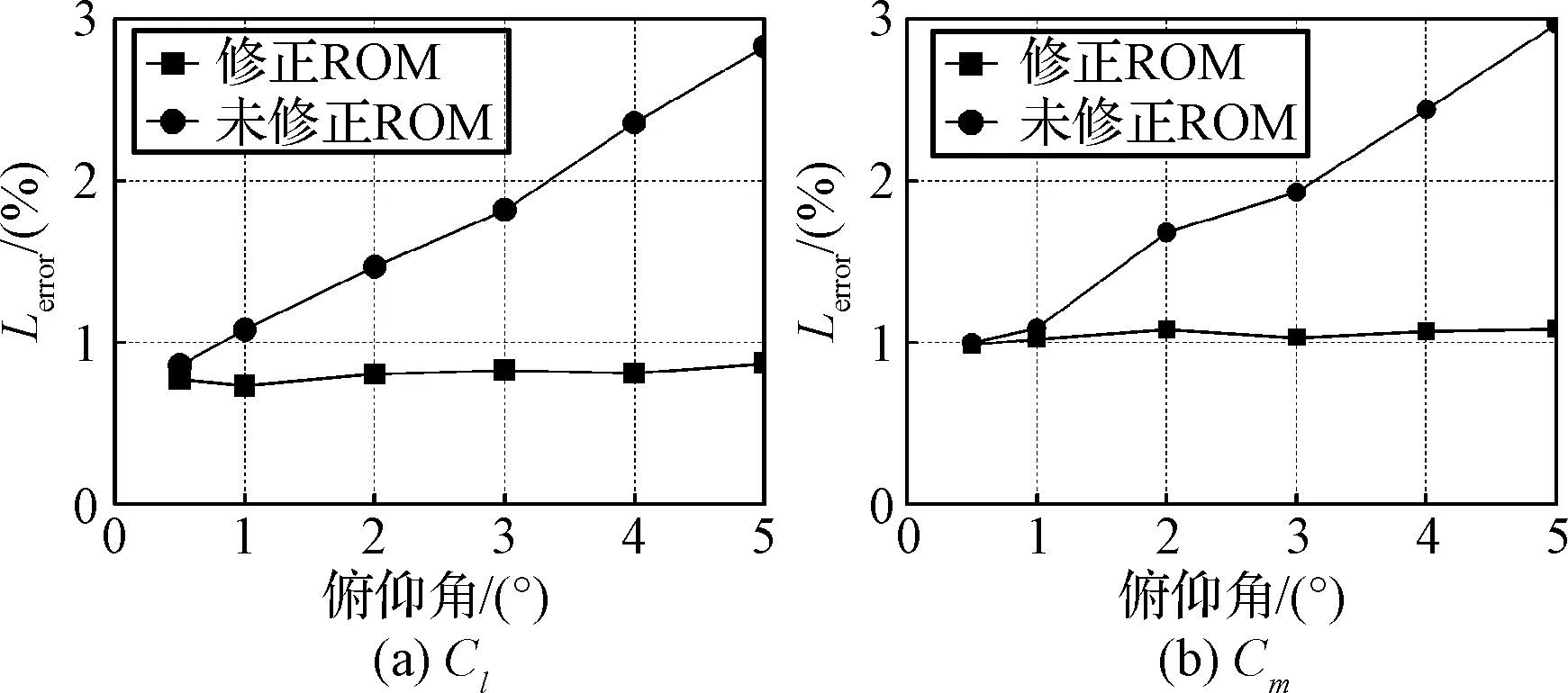
图8 Masim=0.85，俯仰振幅测试误差Fig.8 ROM errors, pitch amplitude tests, Masim=0.85

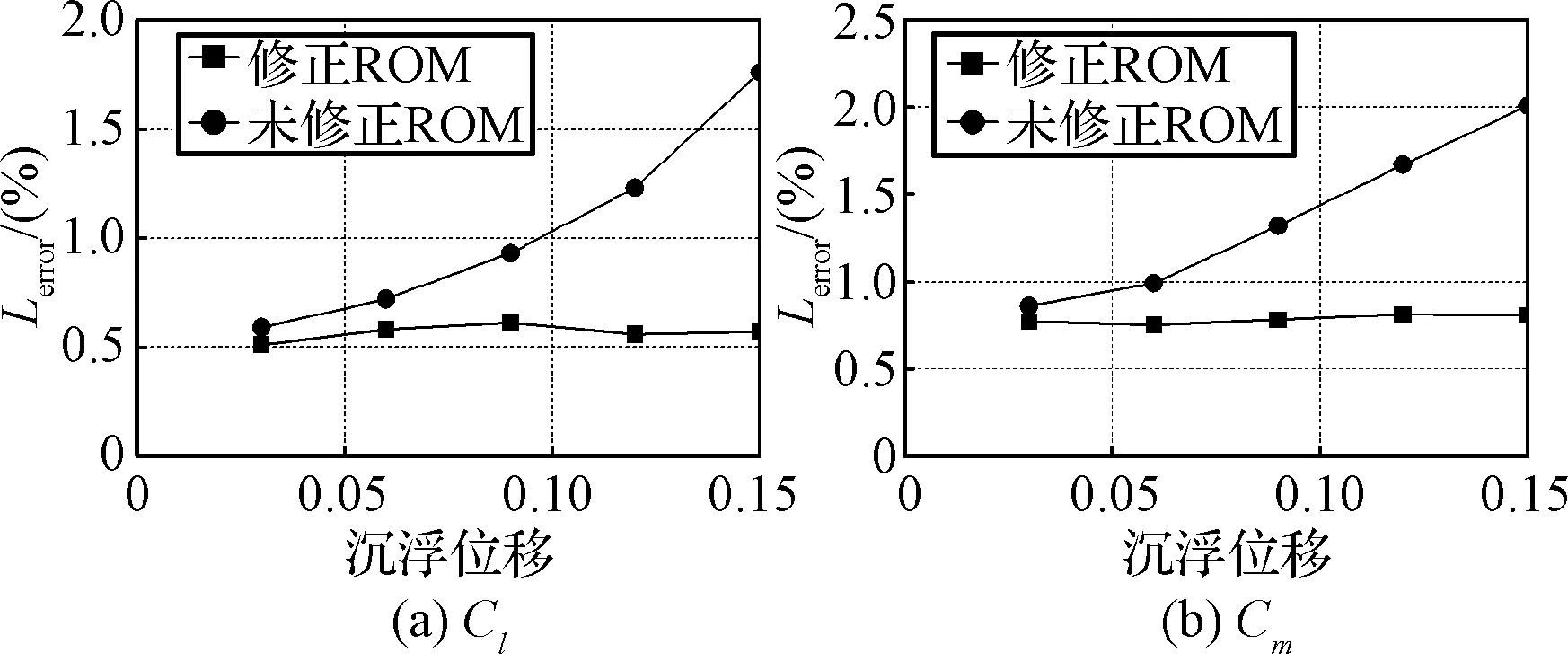
图9 Masim=0.85，沉浮振幅测试误差Fig.9 ROM errors, heave amplitude tests, Masim=0.85

2.6 角频率测试

为了测试减缩频率的增长对ROM精度的影响，现保持马赫数Masim=0.85与振幅d1=4°,d2=0.1不变，考察不同减缩频率下ROM的误差。与振幅测试类似，选取马赫数Mastep=0.85，在减缩频率k=0～0.25的区间内选取6个测试点，如图10所示。升力和力矩系数的误差都保持在1%以内，但是随着减缩频率的增加，误差也在增大，可能是流场内部的不稳定性增加所导致的；另外，力矩系数的误差要比升力系数误差略大。

图10 Ma=0.85，频率测试误差Fig.10 ROM errors, frequency tests, Ma=0.85

2.7 随机振动仿真

在工程实际中，结构往往会发生随机振动，能准确预测这种激励下的非定常气动力对ROM也非常重要。在此，以有限带宽的高斯白噪声(Filtered white Gaussian noise, FWGN)运动规律作为CFD计算的输入，俯仰振幅限制在5°以内，沉浮振幅限制在0.15以内，折合频率为0.02到0.25，计算非定常气动力。FWGN激励下的俯仰和沉浮运动如图11所示。

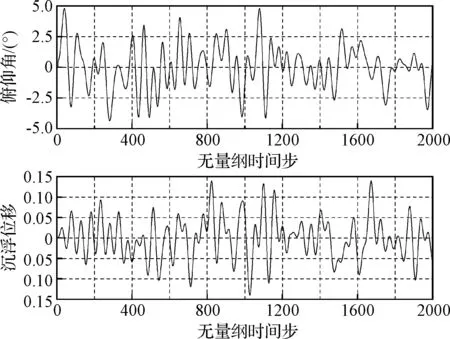
图11 高斯白噪声激励下的俯仰和沉浮振动Fig.11 FWGN input signals for the pitch and heave motions

选取马赫数Mastep=0.85，计算ROM在上述运动状态下的响应值。在上述激励下，ROM和CFD计算的结果如图12所示，可以发现两个结果吻合得很好。对于2000个时间步长非定常气动力的计算，CFD计算花费大约21 min，而ROM只用2.73 s。可见，ROM计算效率要远高于直接CFD方法。

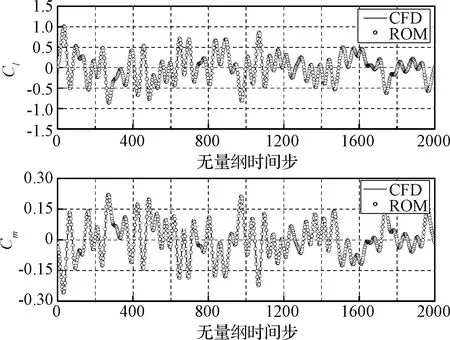
图12 高斯白噪声激励下，ROM结果与 CFD计算结果对比Fig.12 Direct CFD model outputs vs ROM outputs under the FWGN excitation

2.8 气动弹性仿真

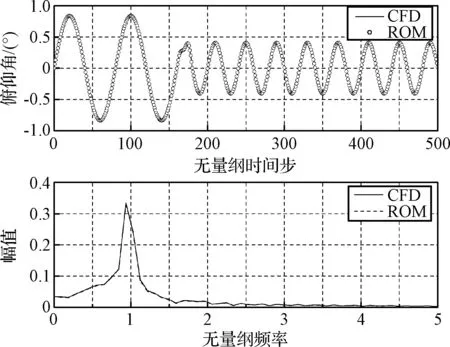
图13 俯仰自由度的气动弹性响应及FFT分析Fig.13 Heave time response and its FFT spectrum

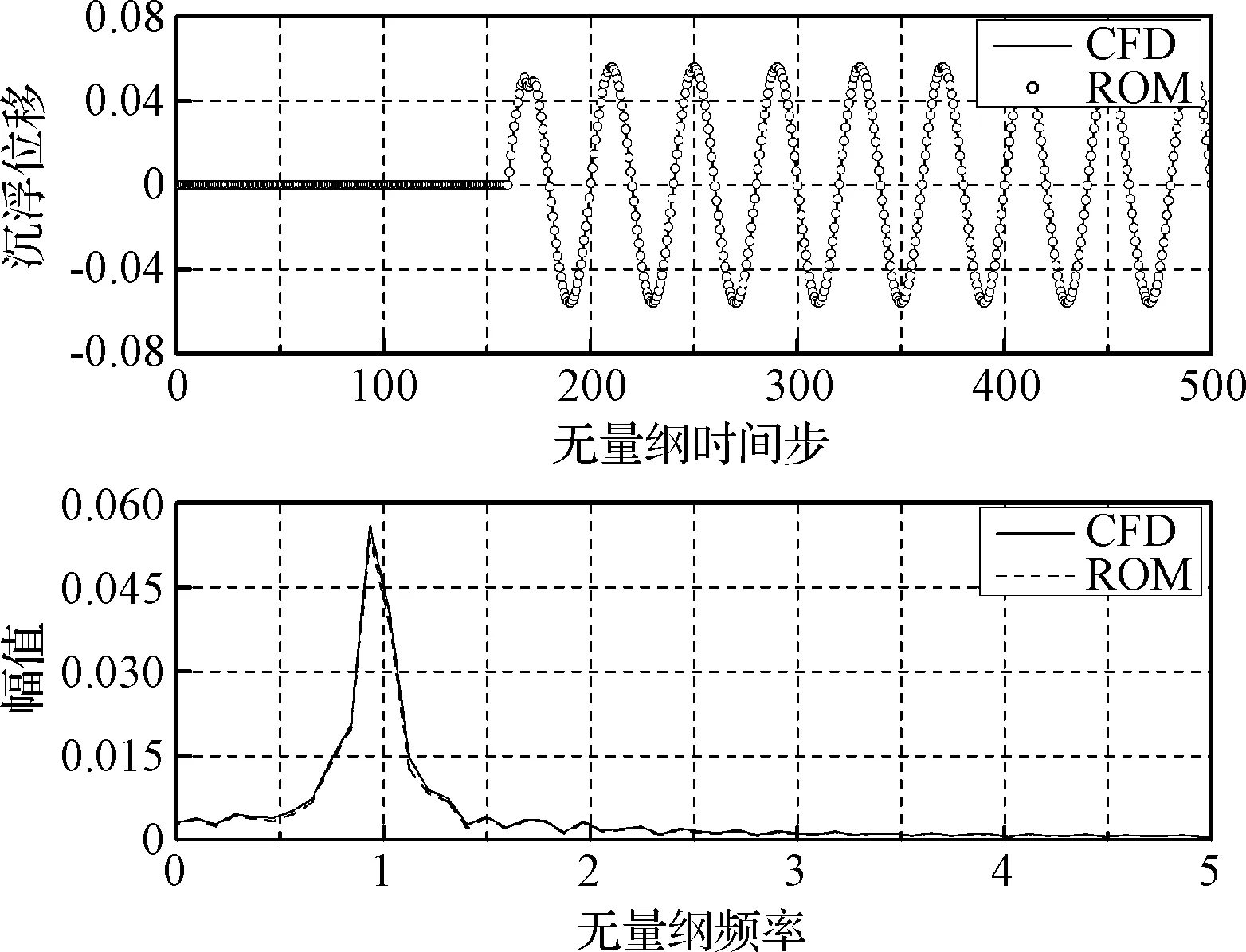
图14 沉浮自由度的气动弹性响应及FFT分析Fig.14 Pitch time response and its FFT spectrum

图15是基于直接CFD方法和ROM方法计算Isogai机翼颤振边界的对比，二者结果基本一致。在马赫数Ma=0.85左右出现跨声速“凹坑”现象，随后颤振速度有个跃升，在Ma=0.875～0.9的区间内又有一个下降，在Ma=0.9之后，颤振速度再次出现很大的跃升，然后缓慢增长，与文献[16]结果一致。

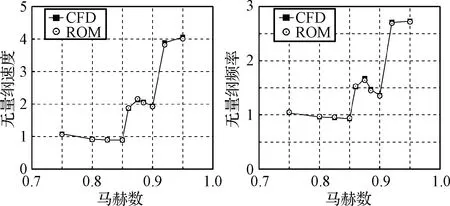
图15 CFD方法和ROM方法预测Isogai机翼的颤振边界Fig.15 Flutter boundaries of the Isogai wing model computed by using direct CFD and ROMs

3 结 论

本文基于线性卷积和修正因子，利用Kriging插值得到参数空间内的修正因子，发展了一种多参数空间的非线性、非定常气动力降阶模型。通过马赫数测试、振幅测试和频率测试，考察其在参数空间内的精度；然后进行随机振动仿真和气动弹性仿真，论证了该ROM的有效性；得到以下结论：

1) 在所考虑的参数空间内，ROM得到了较好的结果，与CFD计算值的比较，误差都在3%以内。在振幅测试中可发现修正后的ROM明显好于未修正的ROM。

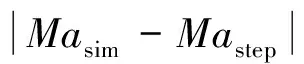
3) 将ROM应用到气动弹性仿真，并且较准确地预测了颤振边界，与CFD/CSD相互耦合方法比较，计算效率大幅提高，若应用到三维机翼，效果将更加明显。

4) 修正因子的引入使该降阶方法具有较好的鲁棒性，可用于主动控制和气动伺服弹性分析与设计。

[1] 陈刚, 李跃明. 非定常流场降阶模型及其应用研究进展与展望[J]. 力学进展, 2011, 41(6):686-701. [Chen Gang, Li Yue-ming. Advances and prospects of the reduced order model for unsteady flow and its application[J]. Advances in Mechanics, 2011, 41(6):686-701.]

[2] Rugh W. Nonlinear system theory: the Volterra/ Wiener approach[M]. Baltimore, MD:Johns Hopkins Univ. Press,1981.

[3] 陈刚, 徐敏, 陈士橹. 基于Volterra级数的非线性非定常气动力降阶模型[J]. 宇航学报, 2004, 25(5):492-496. [Chen Gang, Xu Min, Chen Shi-lu. Reduced-order model based on volterra series in nonlinear unsteady aerodynamics[J]. Journal of Astronautics, 2004, 25(5):492-496.]

[4] 姚伟刚, 徐敏. 基于Volterra级数降阶模型的气动弹性分析[J].宇航学报, 2008, 29(6): 1711-1716. [Yao Wei-gang, Xu Min. Aeroelasticity numerical analysis via volterra series approach[J]. Journal of Astronautics, 2008, 29(6):1711-1716.]

[5] 张子健, 徐敏, 陈士橹, 等. 基于气动力辨识的ASE模型降阶研究[J]. 力学学报, 2009, 41(5): 641-650. [Zhang Zi-jian, Xu Min, Chen Shi-lu, et al. Investigation of model reduction for aeroservoelasticity based on unsteady aerodynamics estimating[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(5):641-650.]

[6] Silva W A. Application of nonlinear systems theory to transonic unsteady aerodynamic responses[J]. Journal of Aircraft, 1993, 30(5):660-668.

[7] Raveh D E, Mavris D N. Reduced-order models based on CFD impulse and step responses[C]. The 42nd AIAA/ASMBASCBAHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Seattle, USA ,Apr 16-19, 2001.

[8] Raveh D E. Identification of computational-fluid-dynamic based unsteady aerodynamic models for aeroelastic analysis[J]. Journal of Aircraft, 2004, 41(3):620-632.

[9] 唐伟，杨肖峰，桂业伟，等. 火星进入器高超声速气动力/热研究综述[J]. 宇航学报, 2017, 38(3): 230-239. [Tang Wei, Yang Xiao-feng, Gui Ye-wei, et al. Review of hypersonic aerodynamics and aerothermodynamics for Mars entries[J]. Journal of Astronautics, 2017, 38(3): 230-239.]

[10] Lind R, Prazenica R, Brenner M, et al. Identifying parameter-dependent volterra kernels to predict aeroelastic instabilities[J]. AIAA Journal, 2005, 43(12): 2496-2502.

[11] Omran A, Newman B. Piecewise global volterra nonlinear modeling and characterization for aircraft dynamics[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(3):749-759.

[12] Omran A, Newman B. Full envelope nonlinear parameter varying model approach for atmospheric flight dynamics[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(1):270-283.

[13] Skujins T, Cesnik C. Reduced-order modeling of hypersonic vehicle unsteady aerodynamics[C]. AIAA Atmospheric Flight Mechanics Conference ,Toronto, Ontario, Canada, Aug 2-5, 2010.

[14] Cioppa T, Lucas T. Effcient nearly orthogonal and space-filling latin hypercubes[J]. Technometrics , 2007, 49(1): 45-55.

[15] Martin J, Simpson T. Use of Kriging models to approximate deterministic computer models[J]. AIAA Journal, 2005, 43(4):853-863.

[16] Zhang Z C, Yang S C, Liu F. Prediction of flutter and LCO by an Euler method on non-moving Cartesian grids with boundary-layer corrections[C]. The 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, Jan 10-13, 2005.

通信地址：南京航空航天大学航空宇航学院(210016)

电话：(025)84892152

E-mail: 994630093@qq.com

赵永辉(1969-)，男，教授，主要从事气动弹性力学、振动主动控制方面的研究。本文通信作者。

通信地址：南京航空航天大学航空宇航学院(210016)

电话：(025)84892152

E-mail: zyhae@nuaa.edu.cn

A Multi-Parameter Space Reduced Order Model ofNonlinear Unsteady Aerodynamics

CHEN Zhi-qiang, ZHAO Yong-hui

(State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

A multi-parameter space reduced order model (ROM) of nonlinear unsteady aerodynamics is proposed based on the linear convolution and correction factor, to obtain the unsteady aerodynamics accurately and efficiently. Firstly, a linear reduced order model is constructed using the convolution of modal step responses. Then, the nearly-orthogonal Latin hypercubes are used to determine the appropriate sampling points in the parameter space, and calculate the correction factor at each sampling point. Finally, the Kriging surfaces for the correction factor are calculated using the Kriging interpolation method, and the modified reduced order model is obtained. The basic geometric model used for the validation of ROM is the Isogai wing. The effects of the Mach number, sinusoidal input amplitudes and oscillation frequency on the accuracy of the ROM are all investigated. The ROM is coupled with the structural model to make a time-marching simulation, and predict the flutter speed. The validation of the ROM in multi-parameter space is proved by the comparison with results obtained via the high-fidelity computation fluid dynamics solver.

Correction factor; Latin hypercube sampling; Kriging interpolation; Nonlinear unsteady aerodynamics; Reduced order model (ROM)

2017- 04-12;

2017- 06- 06

国家自然科学基金(11472128)

V215.3

A

1000-1328(2017)08-0813-09

10.3873/j.issn.1000-1328.2017.08.005

陈志强(1988-)，男，博士，主要从事气动弹性力学和非定常气动力降阶研究。