空间自旋目标混合EFIR/DFT运动轨迹预测算法

2017-09-12黄攀峰刘正雄鹿振宇齐志刚

宇航学报 2017年8期

韩冬，黄攀峰，刘正雄，鹿振宇，齐志刚

(1. 西北工业大学航天学院智能机器人研究中心，西安 710072；2.西北工业大学航天飞行动力学技术重点实验室，西安 710072；3.山西师范大学物理与信息工程学院，临汾 041000)

韩冬1, 2, 3，黄攀峰1, 2，刘正雄1, 2，鹿振宇1, 2，齐志刚1, 2

针对自旋目标运动轨迹的跟踪与预测中鲁棒性与时效性问题，本文提出一种在视觉测量目标位姿的基础上，通过混合扩展有限冲击响应(EFIR)/离散傅立叶变换(DFT)估计目标状态与特征参数，进而预测目标轨迹的方法。在视觉相机对目标特征点位姿测量的基础上，将运动过程分解为平动与转动，时域与频域同步估计目标的状态与动力学参数，采用DFT估计与平动相关参量，采用EFIR估计与转动相关参量，根据空间漂浮目标动力学方程，实现在过程噪声与量测噪声未知的复杂条件下对目标轨迹的长期准确预测，并通过地面机器人模拟试验对预测方法的正确性和有效性开展验证。结果表明：利用本文提出的方法实现了对空间自旋目标运动轨迹的准确预测；与传统基于扩展卡尔曼滤波的预测方法相比，在过程噪声、量测噪声未知的条件下，文中提出的方法有效缩短了参数收敛时间，提高了参数估计与轨迹预测精度。

空间机器人；空间自旋目标；运动轨迹预测；扩展有限冲击响应滤波器；离散傅立叶变换

0 引言

空间机器人具有视觉辨识与运动控制系统，可完成对合作或非合作目标的在轨捕获与释放，执行如轨道垃圾清理、航天器在轨维护等空间任务[1-3]。为完成对目标的在轨服务，在接近与停靠目标的过程中，目标相对空间智能机器人往往存在一定的线速度与角速度，由于信息处理以及位姿解算需要耗费一定时间，因此，实时追踪目标运动轨迹并对运动目标的轨迹进行预测是十分必要的，也是开展目标捕获与在轨服务的基础[4-5]。

国内外许多学者开展了空间智能机器人相关领域的研究，在路径规划方面，Zhou等[6]提出了奇异鲁棒规划方法，解决了路径规划中的算法与动力学奇异问题。在基于视觉的目标识别方面，Linchter等[7]将双卡尔曼滤波器应用到自由漂浮目标的位姿估计中，通过双滤波器差分降低视觉传感器噪声，因为每一次的参数估计都需要进行两次滤波器递归运算，降低了执行器的工作效率，增加了处理时间。Aghili等[8-9]提出了扩展卡尔曼滤波(Extended Kalman filter,EKF)与最近点迭代算法；刘厚德等[10]针对自旋目标运动预测，提出采用无损卡尔曼滤波方法，但是这些方法均需要预先估计量测噪声与过程噪声的协方差，这对于空间任务来说是十分困难的。Hillenbrand等[11]利用最小二乘法对空间目标进行参数辨识与运动估计，这种方法在发生遮挡、抖动等情况造成非等间隔采样的条件下会显著降低预测精度。

前期的研究工作以及地面验证试验表明，在目标位置坐标获得过程中，可能出现的相机抖动、光照变化、目标漂浮及遮挡等影响，造成采样时间较短，采样过程不连续及测量噪声与过程噪声未知等问题[12]。因此，设计基于位姿测量信息，对目标运动轨迹进行追踪与预测的鲁棒性算法便十分必要。

本文首先假设已经获得了带有噪声的目标位姿测量数据，在空间自旋目标动力学方程的基础上，设计EFIR/DFT滤波器，为满足滤波器的要求，对目标动力学方程进行了线性化，从而实现运动状态信息与动力学参数的准确估计，最后根据动力学方程，获得目标的轨迹预测。本文算法的特点在于通过分别处理平动与转动，减少了估计状态，提高了收敛速度。通过采用加窗的方法，避免了噪声累加对估计值的影响，在噪声统计特性未知的条件下有更好的估计效果，对扰动有更强的鲁棒性，提高了复杂条件下自旋目标的轨迹预测精度。

1 空间自旋目标运动学与动力学建模

本文主要研究对象为漂浮旋转目标，为预测目标的运动轨迹，首先建立空间坐标系模型，如图1所示。坐标系{A}为惯性坐标系，坐标系{B}为固联于卫星本体的坐标系，卫星质心O为坐标系{B}原点，坐标轴平行于卫星主惯量轴。坐标系{C}以目标点为原点，坐标轴平行于帆板支架，坐标系{C} 的位姿通过视觉系统测量获得。ρ为卫星质心到目标点位置矢量，ω为目标旋转角速度，ρ,ω均为在坐标系{B}下的表达。

空间自旋目标姿态运动学建模可以采用方向余弦矩阵、四元数以及修正的罗德里格参数等，文献[13]提供了一种微分建模思路，为使无穷小角位移描述形式简单，本文采用四元数描述空间自旋目标姿态运动学，坐标系{B}相对于{A}的旋转通过四元数q表示，运动学方程可表示为：

(1)

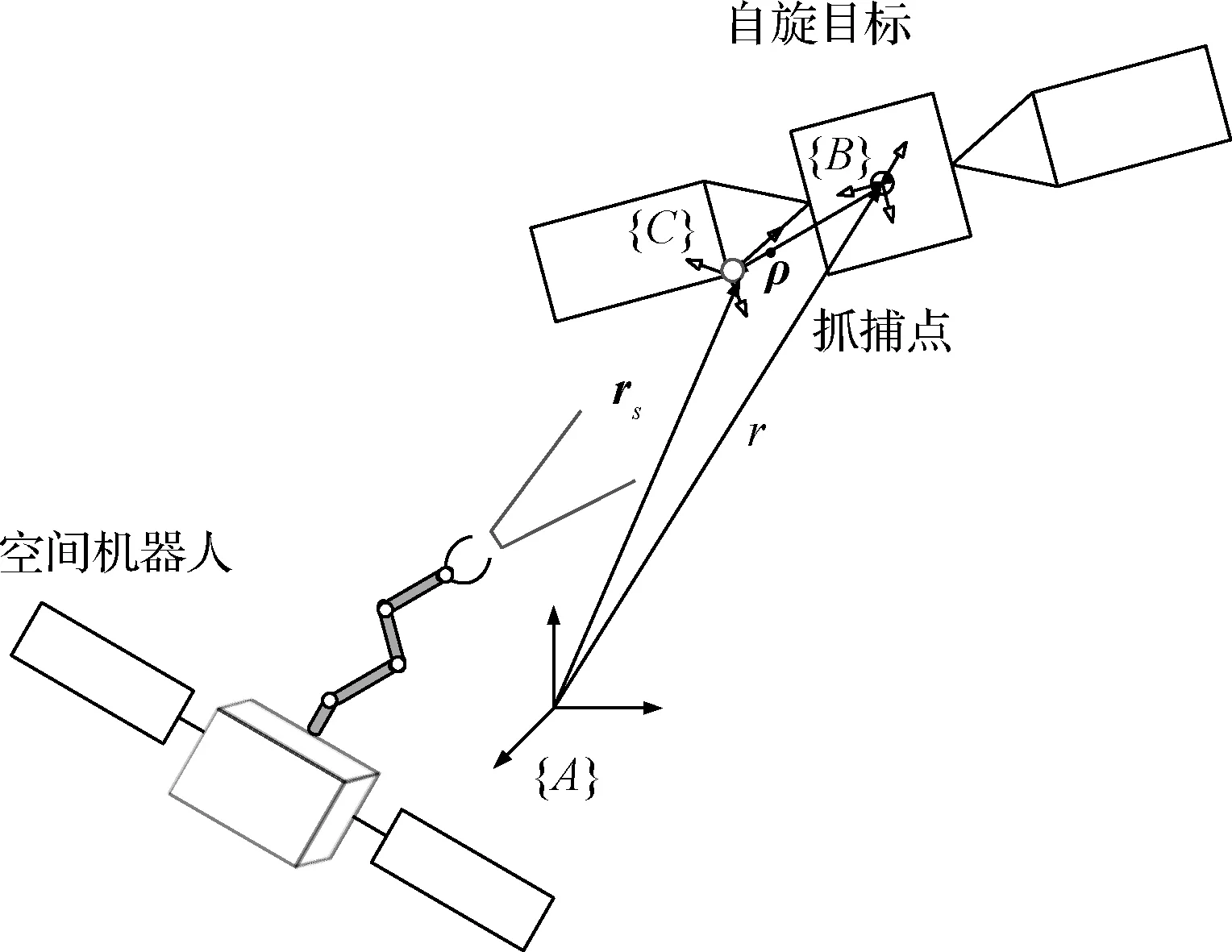
图1 空间自旋目标轨迹预测Fig. 1 Trajectory prediction of space spinning target

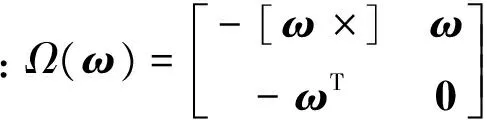
q⊗≜q0E4+Ω(qv)

(2)

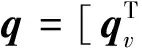
R(q)=(2q02-1)E3+2q0[qv×]+2qvqvT

(3)

为了估计目标的运动状态与参数，建立通过欧拉方程描述的目标姿态动力学方程：

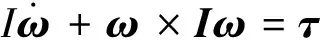
(4)

式中：I为转动惯量，τ为扰动力矩，根据漂浮目标动力学方程，当τ=0时无法通过目标运动轨迹分别独立估计出三个方向转动惯量，为解决这个问题，引入惯量参数表示：

(5)

式中：Ixx,Iyy,Izz为目标主惯量，应满足以下条件：

进而可求得惯量参数的约束条件

px>-1,py>-1,pz>-1

用惯性参数改写动力学方程为：

(6)

式中:

Ic=diag(Ixx,Iyy,Izz)。tr(Ic)表示Ic的迹，ετ用来描述太阳能帆板支架、重力梯度等产生的阻尼效果，可以选择采用过程噪声来描述。

目标点的位置与速度表达式可由以下方程描述：

rs=r+R(q)ρ=r0+vt+R(q)ρ

(7)

(8)

至此，通过式(1)、(4)及其简化与变形获得了空间自旋目标的运动学与动力学方程。式(7)、(8)描述了目标的运动状态。

2 EFIR/DFT滤波器设计与目标轨迹预测

为了实现对运动目标的轨迹预测，需要获得目标的动力学参数，因为测量系统仅能提供目标的位姿信息，所以有必要对动力学模型中的未知参数进行估计。根据式(7),考虑到运动目标平动与转动的可分解性，分别设计了频域与时域的估计滤波器，对于平动参量采用频域最优滤波器DFT估计目标卫星质心位置及线速度。对于转动参量采用时域EFIR滤波器估计运动状态与动力学参数。考虑到动力学方程的非线性无法满足线性滤波器的要求，首先对动力学方程进行了线性化。

2.1 量测方程线性化

假定视觉测量系统可以获得带有噪声的目标点相对位姿并可解算到惯性坐标系下，如图1所示，目标位置由矢量rs表示，目标所在坐标系{C}相对于惯性坐标系{A}的姿态由四元数η表示，测量向量Z可表示为：

(9)

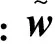
η=μ⊗q

(10)

式中:⊗为四元数乘，定义与转动有关的状态矢量：

(11)

式中：qv,μv分别为四元数的矢量部分。则观测方程中转动部分可表示为：

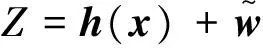
(12)

式中:

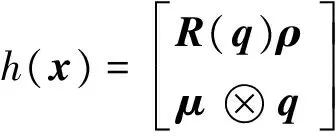
(13)

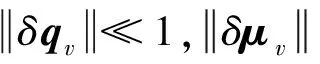
(14)

描述微小旋转的四元数方程：

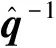
(15a)

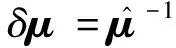
(15b)

将式(15)代入式(10)并忽略高阶小项可得：

(16)

式中：

Γ=

至此，式(14)、(16)给出了观测方程的一阶近似值，并可以由此得出量测矩阵：

(17)

2.2 状态方程线性化

根据式(1)、(6)所描述的目标动力学方程，将连续时间状态空间模型描述为：

(18)

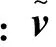
(19a)

(19b)

对于方程(6)的线性化可直接由全微分公式给出：

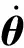
将方程(18)写成离散形式，有

X(n)=Φ(n)X(n-1)+v(n)

(20)

其中，v(n)表示离散的过程噪声，Φ(n)表示离散状态转移矩阵。对于离散系统有

Φ(n) ≜Φ(tn+1,tn)=Φ(tn+1-tn)=

eF(tn)(tn+1-tn)≈E15+(tn+1-tn)F(tn)

(21)

2.3 混合EFIR/DFT滤波器设计

满足无偏要求的扩展有限冲击响应(EFIR)滤波器最早由Shmaliy[15]提出，不同于采用递归算法的卡尔曼滤波器，EFIR滤波器采用迭代算法，因为在算法中做了加窗处理，不会产生因持续的偏差累计而导致滤波器发散的现象，鲁棒性好。但是，加窗的影响会增加计算量，使收敛时间变长，针对这一问题，本文根据式(7)～(8)将目标运动分解为相对惯性系的平动与转动，分别进行时域与频域处理，对于平动采用离散傅立叶变换(DFT)估计质心位置与线速度，对于转动则采用扩展有限冲击响应(EFIR)滤波器估计角速度、惯性参量及目标点距质心位置，从而降低了估计维数，提高了收敛速度。

2.3.1 DFT滤波器设计

对目标位置序列进行DFT变换，相当于把这个序列通过一个FIR数字滤波器，位置序列rs(n)的离散傅立叶变换式

(22)

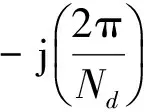
根据式(7)、(8)，质心位置r0与线速度v均为目标位置序列及其差分的直流分量，因此可通过DFT滤波器准确估计出，并且由于估计值为直流分量，因而对高频观测噪声以及信号的非等间隔采样具有很强抑制性。理论上角速度为周期函数，也可由DFT估计得出，但由于估计需要满足最低周期要求，这需要观测最小一个周期的时间，这会使得观测时间过长，正是这个原因使我们提出了通过EFIR滤波器进行角速度与动力学参数估计。

2.3.2 EFIR滤波器设计

将离散线性系统模型采用状态空间法进行描述，由式(12)、(20)描述的状态矩阵和观测矩阵表示为：

Xn=ΦnXn-1+Vn

(23)

Zn=HnXn+Wn

(24)

其中，过程噪声与量测噪声均假定为零均值分布的高斯白噪声，并且假定彼此互不相关。设计EFIR滤波器的有效观测长度N，这可以通过地面试验获得，也可以通过计算量测偏差的均方值在线估计得出[16]。当获得第n时刻量测值时，从时刻m=n-N+1到时刻n之间的N个量测值为有效量测值，为保证系统的因果性，需要满足m≥0，即n≥N-1。

目标n时刻状态的估计值可以表示为

(25)

其中

而

该算法是使用正交条件，通过优化估计均方误差最小原则获得，其优点是能够在噪声统计特性未知的情况下对信号进行估计，当N=Nopt时可以获得近似最优估计。其不足之处在于N的增大会导致矩阵维数的增大，从而使计算量增加，求解速度减慢。引入类卡尔曼滤波器的迭代算法可以很好地解决这一问题，目标状态的迭代估计值为

(26)

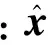
(27)

式中:Gl为广义噪声功率增益，通过下式迭代计算得出

(28)

可见，Gl的计算仅需已知矩阵Hl与Φl，Hl为l时刻观测矩阵，Φl为l时刻状态转移矩阵，在滤波器增益计算中，不需要预测噪声统计特性，该特点使算法适合噪声特性未知的复杂条件下空间任务。算法流程如图2所示。

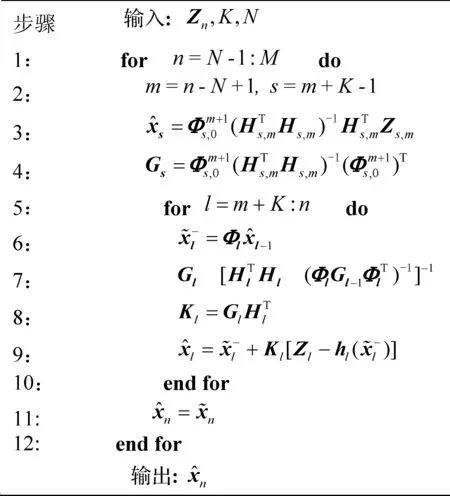
图2 EFIR滤波算法Fig.2 EFIR filter algorithm

2.4 目标轨迹预测

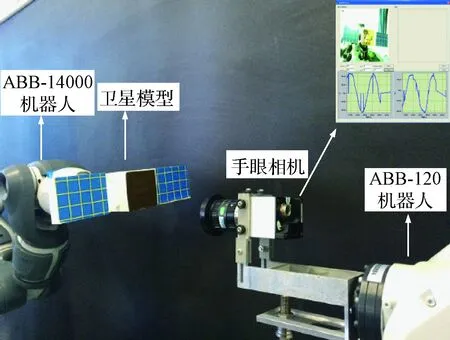
图3 测量系统实验平台Fig. 3 The equipment of measuring system

3 试验验证

为验证本文提出的混合EFIR/DFT轨迹预测算法的正确性，现利用两台机器人对其进行运动学试验验证，测试平台如图3所示，采用ABB-14000机器人抓持卫星模型，该机器人具有6自由度，可以根据航天器零重力空间动力学模型解算出轨迹精确的模拟漂移与自旋运动，采用ABB-120机器人模拟空间平台，机械臂末端装备手眼相机，通过振动模拟平台随机抖动。手眼相机采集目标位置数据并解算姿态信息，数据采样频率为10 Hz，采样数据传输到上位机中进行处理。

卫星模型的转动惯量设计为Ixx=0.08 kg·m2,Iyy=0.04 kg·m2,Izz=0.05 kg·m2，由此可根据式(8)计算得到惯性参量值

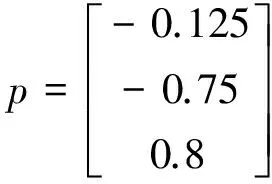
R=diag((0.015)2E3m2,(0.04)2E4)

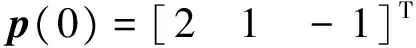
试验首先通过视觉系统获得目标的位姿数据，由于目标与相机所处角度的不同所导致的光照变化及机械臂的振动，造成了采样数据的非平稳，量测数据如图4所示。根据获得的量测数据，频域上通过DFT算法估计目标质心位置及漂移线速度，离散傅立叶变换是频域上的最优估计，如图5所示，其中质心位置的估计采用128个数据点，12.8 s即可完成采样，平均误差0.019 m。线速度的估计采用256个数据点，平均误差0.45 mm，数据中的有限零点并不影响估计结果，对非平稳采样有较强的鲁棒性,其中估计误差仅与采样点数目有关，采样点增加可提高估计精度。时域上通过EFIR算法估计动力学参数与目标相对质心位置及旋转角速度，根据状态数选取批处理长度K=5，并通过计算求出此时UFIR滤波器最优窗长Nopt=37[16]，估计结果如图6所示，从试验结果可以看出，估计值较准确地收敛到了真值。

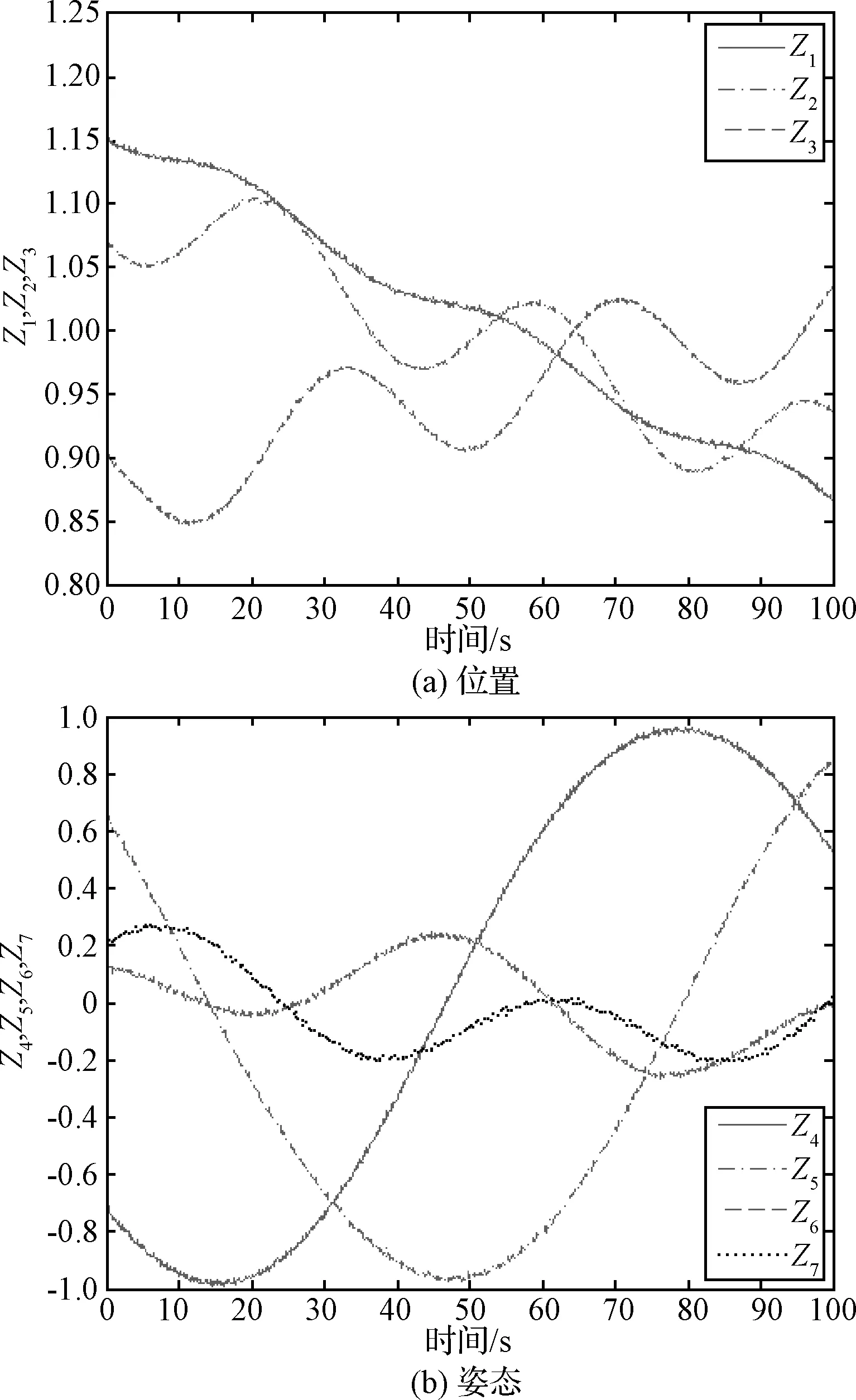
图4 手眼相机测量目标位置与姿态Fig. 4 Target pose measurements obtained from hand-eye camera

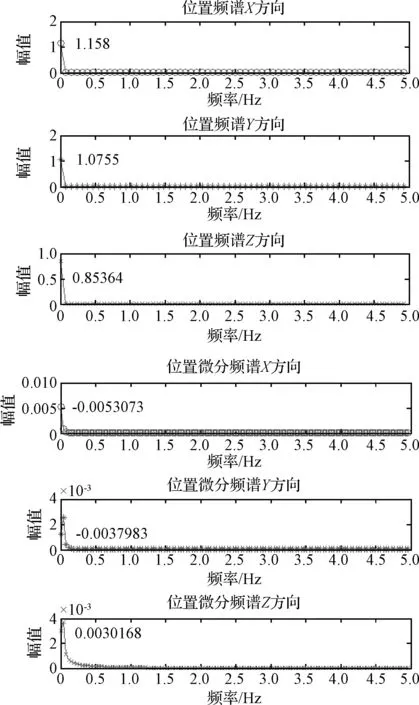
图5 DFT滤波器质心位置与线速度估计Fig. 5 Estimate position of the target center of mass and drift velocity with DFT filter

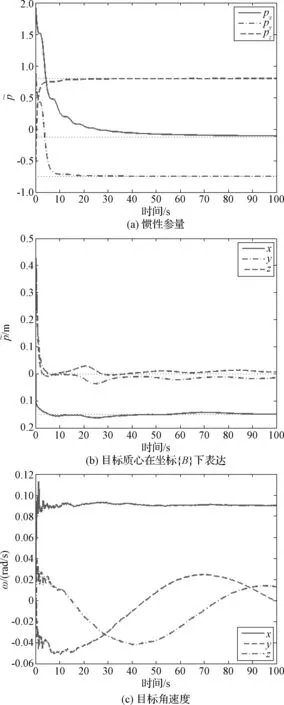
图6 EFIR滤波器目标参数估计Fig. 6 Estimate parameters of the target with EFIR filter

选取一步预测协方差的欧几里得范数作为估计值收敛的判断，当范数值小于设定的闸值时对已采样数据进行DFT变换。

对于εth的选取兼顾了准确性与收敛时间的矛盾，增大闸值可以缩短收敛时间，但也会降低预测精度。本文将闸值设定为0.2，满足后续抓捕对预测精度的要求。由图7可知，与通常采用的EKF相比，本文提出的算法由于采用了时域与频域的同步处理，降低了估计维度，缩短了收敛时间。

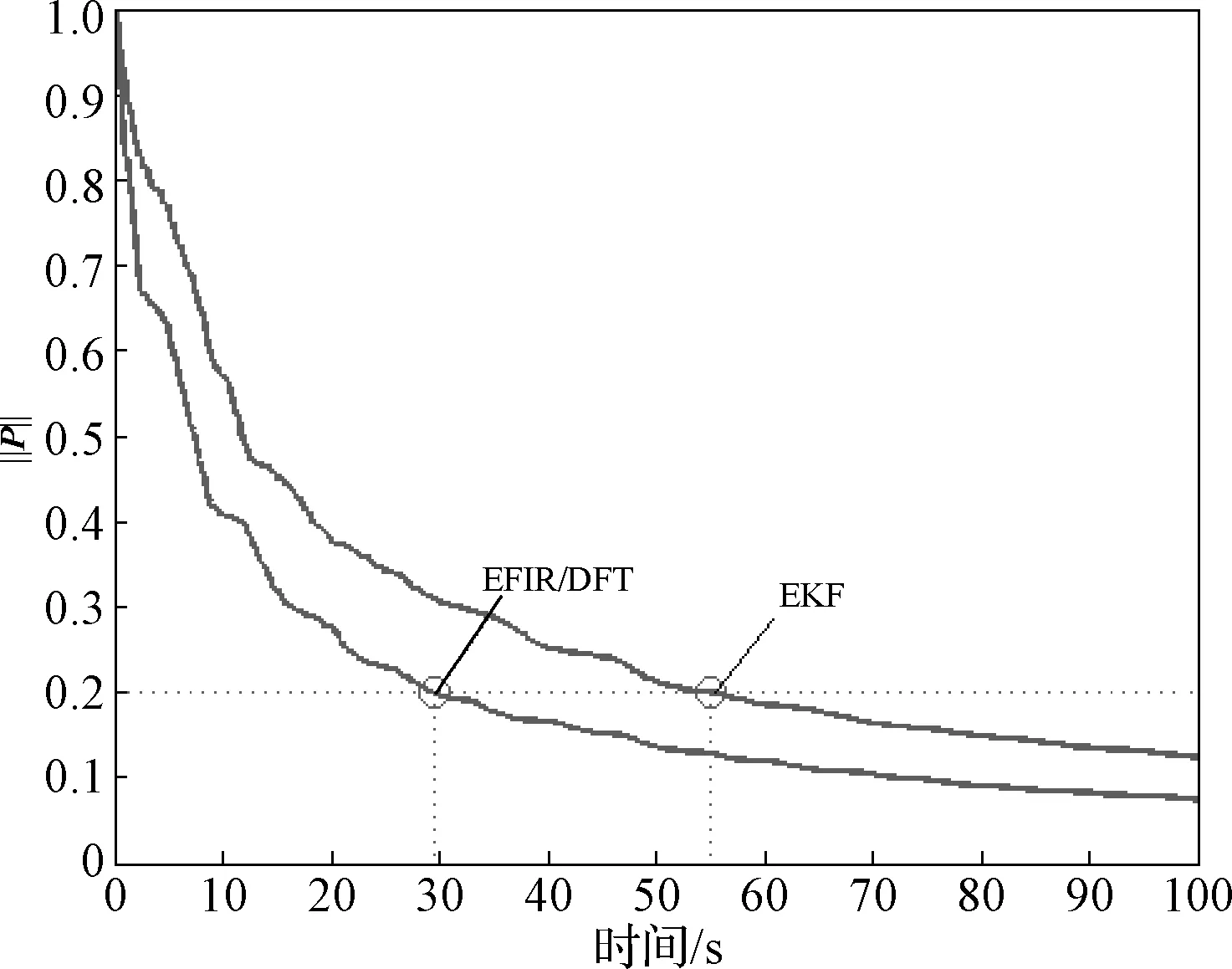
图7 估计器收敛检测Fig. 7 Detecting the estimator convergence

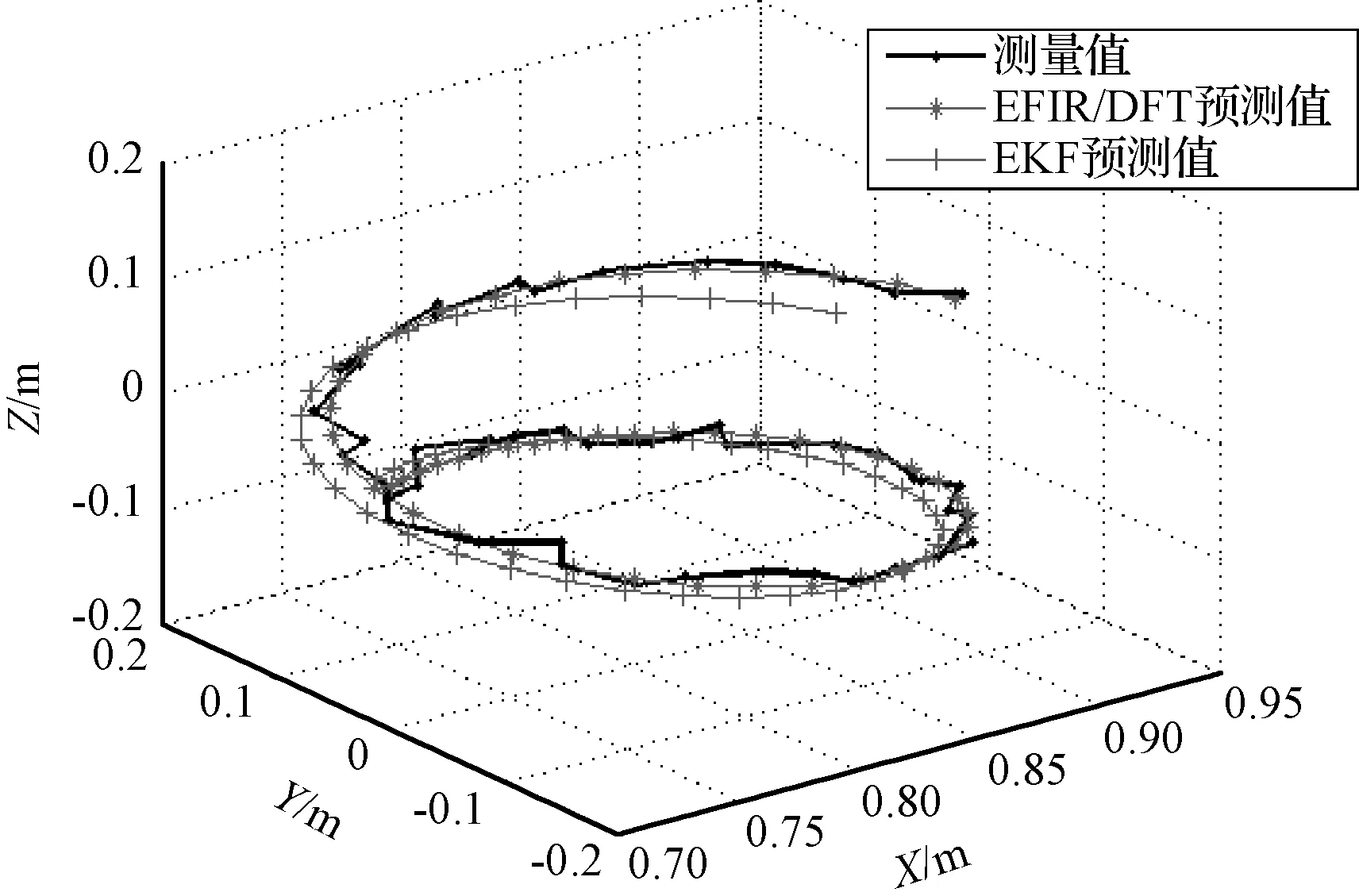
图8 目标轨迹预测结果Fig. 8 Predictive results of target trajectory

为比较不同方法获得的轨迹预测准确度，选取EKF作为比较对象，通过计算实验结果与预测值的均方根偏差作为准确性评估标准

(29)

式中：δx,δy,δz为实验结果与预测值在x轴，y轴，z轴的差值。本文算法的均方根偏差值为0.0120，EKF的均方根偏差为0.0175 。可见在噪声参数未知的条件下，本文提出的算法具有更高的准确性。

4 结论

本文针对空间抓捕任务中的自旋目标轨迹预测问题，提出了混合EFIR/DFT滤波算法，根据公式的推导与试验的结果可得出如下结论：

1)在空间变化的光照环境与不确定的量测角度等复杂条件下，目标的视觉识别会产生采样的不连续，过程噪声与量测噪声的不可预知等问题，在这种条件下，算法鲁棒性便愈加重要，本算法采用的EFIR算法通过时域加窗来解决估计偏差累计造成的估计发散问题，具有较强的鲁棒性。

2)本文算法在时域与频域同步对采样数据进行处理，与传统的仅从时域对数据进行处理相比，最大限度的使用了采样数据所提供的信息，将时域滤波器的维度从7维降低到5维，并且不需要预估噪声统计特性参数，针对复杂噪声的空间环境，可以有效地减少滤波器的收敛时间。

3)机械臂模拟目标运动学试验证实，在噪声环境未知的条件下，本文所提出算法的准确性优于传统扩展卡尔曼滤波算法，能够实现对目标位置的长期预测。

[1] 刘正雄,鹿振宇,黄攀峰. 基于递推差分进化算法的空间机器人参数辨识[J]. 宇航学报, 2014(10):1127-1134 .[Liu Zheng-xiong, Lu Zhen-yu, Huang Pan-feng. Parameter identification of space robot based on recursive different evolution algorithm[J]. Journal of Astronautics, 2014(10):1127-1134.]

[2] 张帆,黄攀峰. 空间绳系机器人抓捕非合作目标的质量特性参数辨识[J]. 宇航学报, 2015(6):630-639.[Zhang Fan, Huang Pan-feng. Inertia parameter estimation for an non-cooperative target captured by a space tethered system[J]. Journal of Astronautics, 2015(6):630-639.]

[3] 蔡佳,黄攀峰,王东科,等. 空间绳系机器人单目视觉伺服控制系统[J]. 宇航学报, 2015(2):133-141.[Cai Jia, Huang Pan-feng, Wang Dong-ke, et al. Monocular visual servo control system scheme for tethered space robot[J]. Journal of Astronautics, 2015(2):133-141.]

[4] Angel F A,Ou M, Khanh P, et al. A review of space robotics technologies for on-orbit servicing[J]. Progress in Aerospace Sciences, 2014, 68: 1-26.

[5] 梁斌, 徐文福, 李成, 等. 地球静止轨道在轨服务技术研究现状与发展趋势[J]. 宇航学报, 2010, 31(1): 1-13.[ Liang Bin, Xu Wen-fu,Liu Cheng, et al. The status and prospect of orbital servicing in the geostationary orbit[J]. Journal of Astronautics, 2010, 31(1): 1-13.]

[6] Zhou C, Jin M H, Liu Y C, et al. Singularity robust path planning for real time base attitude adjustment of free-floating space robot [J]. International Journal of Automation and Computing, 201714(2): 169-178.

[7] Lichter M D, Dubowsky S. State, shape, and parameter estimation of space objects from range images[C].Robotics and Automation, ICRA′04, New Orleans, USA, April 26-May 1, 2004.

[8] Aghili F. A prediction and motion-planning scheme for visually guided robotic capturing of free-floating tumbling objects with uncertain dynamics [J]. IEEE Transactions on Robotics, 2012, 28(3): 634-49.

[9] Aghili F, Kuryllo M, Okouneva G, et al. Fault-tolerant position/attitude estimation of free-floating space objects using a laser range sensor [J]. IEEE Sensors Journal, 2011, 11(1): 176-85.

[10] 刘厚德, 梁斌, 徐文福, 等. 自旋目标运动预测及自主捕获路径规划方法 [J]. 吉林大学学报(工学版), 2014(3): 757-764. [ Liu Hou-de, Liang Bin, Xu Wen-fu, et al. Motion prediction and autonomous path planning for spinning target capturing[J]. Journal of Jilin University (Engineering and Technology Edition), 2014(3): 757-764.]

[11] Hillenbrand U,Lampariello R. Motion and parameter estimation of a free-floating space object from range data for motion prediction[C].SAIRAS, Munich, Germany, September 5-8, 2005.

[12] Wensong J, Zhongyu W, Mourelatos Z P. Application of nonequidistant fractional-order accumulation model on trajectory prediction of space manipulator [J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(3): 1420-1427.

[13] Zhou C, Jin M, Liu Y, et al. Motion planning for redundant free-floating space robot with local optimization of reaction torque andjoint torque simultaneously[C]. IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, Dec. 3-7, 2016.

[14] Pittelkau M E. Kalman filtering for spacecraft system alignment calibration [J]. Journal of Guidance, Control, and Dynamics, 2001, 24(6): 1187-1195.

[15] Shmaliy Y S. An unbiased FIR filter for TIE model of a local clock in applications to GPS-based timekeeping [J].Ieee Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2006, 53(5): 862-870.

[16] Ramirez-Echeverria F, Sarr A, Shmaliy Y S. Optimal memory for discrete-time FIR filters in state-space [J]. IEEE Transactions on Signal Processing, 2014, 62(3): 557-561.

韩冬 (1983-) 男，博士生,主要从事空间机器人学、复合体稳定控制等研究。

通信地址：西安市友谊西路127号(710072)

电话：13934179244

E-mail:alexcn@mail.nwpu.edu.cn

黄攀峰(1974-) 男，博士，教授,主要从事空间机器人学、空间遥操作等研究。本文通信作者。

通信地址：西安市友谊西路127号(710072)

电话：(029)88460366

E-mail:pfhuang@nwpu.edu.cn

A Hybrid EFIR/DFT Algorithm on TrajectoryPrediction of Space Spinning Target

HAN Dong1, 2, 3, HUANG Pan-feng1, 2, LIU Zheng-xiong1, 2, LU Zhen-yu1, 2, QI Zhi-gang1, 2

(1. Research Center of Intelligent Robotics, School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;2. National Key Laboratory of Aerospace Flight Dynamics, Northwestern Polytechnical University, Xi’an 710072, China;3. School of Physics and InformationEngineering, Shanxi Normal University, Linfen 041000, China )

Based on the visual camera, a robust and efficient method for tracking and predicting the trajectory of a space spinning target is proposed in this paper. The initial discrete point set of a motion trajectory is firstly accumulated in real-time, and then the motion is decomposed into translation and rotation. A hybrid extended finite impulse response (EFIR)/discrete Fourier transform (DFT) is used to estimate the states and dynamics parameters in time domain and frequency domain simultaneously. According to the dynamic equations of a free-floating object, we achieve the long-term and precise prediction while the measurement noise and process noise are unknown. The experiment with ground robot is presented to verify the correctness and effectiveness of the proposed method. The results show that the trajectory of a space spinning target can be predicted accurately using our proposed method. Comparing with the traditional extended Kalman filtering algorithm, the presented control method can improve the the speed of the parameter estimation and the accuracy of the trajectory prediction despite the noise covariance and the initial conditions are not exactly known in advance.

Space robot; Space spinning target; Trajectory prediction; Extended finite impulse response; Discrete Fourier transform

2017-03-10;

2017-05-31

国家自然科学基金(11272256，60805034，61503231)

V448.2

1000-1328(2017)08-0804-09

10.3873/j.issn.1000-1328.2017.08.004