基于自适应抗扰控制策略的太阳电池 MPPT的研究

张 兵，杨子林*，郭亚男

(1.南阳农业职业学院机电工程学院，南阳 473000；2. 郑州经贸学院 智慧制造学院，郑州 450000)

0 引言

在一定的太阳辐照度和环境温度下，太阳电池可直接将太阳能转换成电能[1]，这种发电形式称为光伏发电。太阳电池在某一输出电压值时，其输出功率能达到最大值，光电转换效率达到最高，此时太阳电池中输出功率-电压曲线的工作点达到最高，此点被称为最大功率点[2]。根据太阳电池等效电路原理图，通过设计智能控制器来预测太阳电池可能达到的最大功率点输出，改变当前电路中的阻抗值，调整太阳电池输出功率-电压曲线的工作点，从而保持太阳电池一直运行在最大功率点附近，此工作过程被定义为最大功率点跟踪(maximum power point tracking，MPPT)[3]。

为提高光伏发电系统的发电效率，需使太阳电池的工作点保持在最大功率点附近。基于此，本文提出了一种基于自适应抗扰控制策略的太阳电池MPPT。根据太阳电池的特性在MATLAB/Simulink中建立太阳电池的仿真模型，对不同环境下的太阳电池输出特性进行建模和仿真，采用扩张状态观测器(ESO)观测太阳电池的电压和功率，预测其当前工作点与最大功率点的位置关系，自适应抗扰控制器会根据太阳电池的变化实时调整其工作点，从而实现对扰动的主动抑制，使太阳电池的工作点保持在最大功率点附近。

1 太阳电池仿真模型的建立与特性分析

1.1 光伏发电系统的原理结构

光伏发电的工作原理是利用光生伏特效应将太阳的辐射能量直接转换为电能。光伏发电系统通常分为独立式光伏发电系统、并网式光伏发电系统和混合发电系统。其中，独立式光伏发电系统主要由光伏阵列、控制器、蓄电池组和逆变器构成。独立式光伏发电系统的基本组成如图1所示。

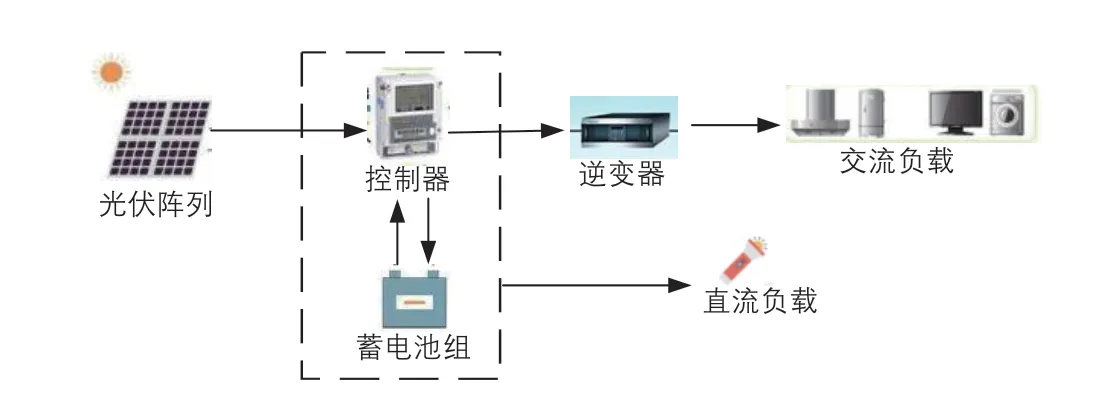
图1 独立式光伏发电系统的基本组成Fig. 1 Basic composition of independent PV power generation system

1.2 太阳电池仿真模型的建立

太阳电池的等效电路图如图2所示。图中：V为太阳电池的输出电压，V；I为太阳电池的输出电流，A；IL为太阳电池的光生电流，A；Id为二极管的导通电流，A；Rsh为太阳电池的等效电阻，Ω；Ish为太阳电池的等效电流，A；Rs为太阳电池的串联电阻，Ω。

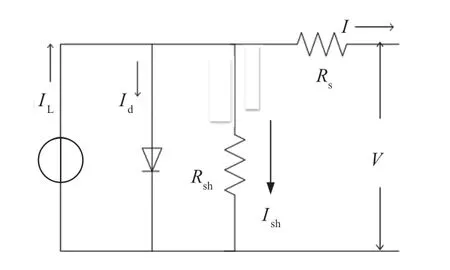
图2 太阳电池的等效电路图Fig. 2 Equivalent circuit of solar cell

太阳电池在正常发电状态下，其电流方程可表示为：

其中，Id可表示为：

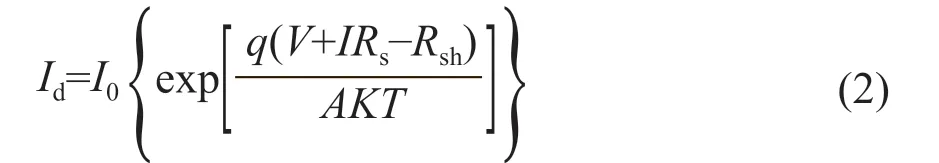
式中：I0为太阳电池的反向饱和电流，A；q为单位电荷量；A为二极管因子；T为太阳电池p-n结的绝对温度，K；K为普朗克常量。

Ish可表示为：

将式(2)、式(3)代入式(1)，可得到：

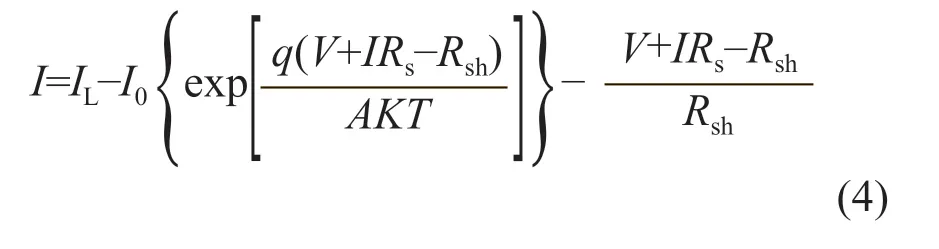
根据太阳电池的物理学原理和数学原理，存在以下情况：

1)由于(V+IRs)/Rsh项的值远小于光生电流，因此本项可省略；

2)太阳电池正常运行时，Rs值远小于正向导通电阻，因此设定V=Voc，太阳电池最大功率点处的电压Vm=V、电流Im=I。其中，Voc为太阳电池的开路电压，V。

根据上述情况对式(4)进行整理，可得：

式中：C1、C2均为温度系数常数；Isc为太阳电池的短路电流，A。

则此时Im可表示为：

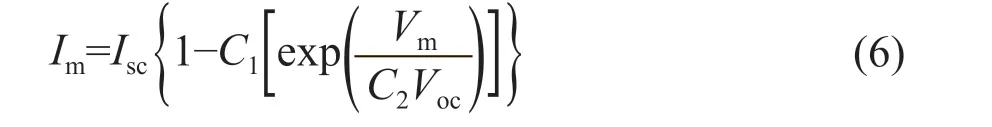
在开路状态下，当I=0时，V=Voc，因此式(5)可以表达为：

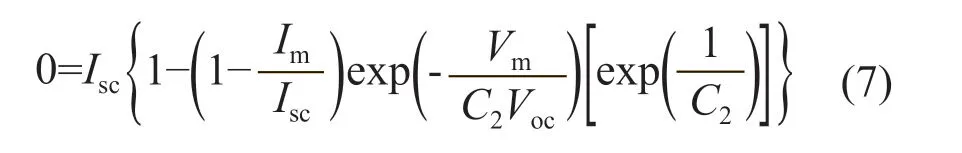
从式(7)可以看出，太阳电池的I-V特性曲线与太阳辐照度和太阳电池的工作温度有关。地面上太阳辐照度S的变化范围为0～1000 W/m2，太阳电池的工作温度的变化范围为0～60 ℃[4]。

任意太阳辐照度S、环境温度Tair与太阳电池p-n结的绝对温度T三者之间存在如下关系：

式中：J为常量，℃·m2/W，本文取0.0289。通过对标准测试条件的太阳辐照度和标准测试条件的太阳电池工作温度下太阳电池I-V特性曲线上任意点(V，I)的移动，可得到新的太阳辐照度和新的太阳电池工作温度下太阳电池I-V特性曲线上任意点(V′，I′ )的表达式，即[5]：

式中：α为标准测试条件的太阳辐照度下太阳电池的电流温度系数，%/℃，根据太阳电池实测值，α=0.00267Isc；β为标准测试条件的太阳辐照度下太阳电池的电压温度系数，%/℃，根据太阳电池实测值，β=0.0671Voc；Tref为标准测试条件下的环境温度，℃；Sref为标准测试条件下太阳电池的工作温度，℃。

针对太阳电池的工作过程和输出特性，考虑太阳电池光电转换效率影响因素，建立太阳电池的数学模型。根据数学模型进行MATLAB/Simulink仿真，建立太阳电池仿真模型，从而获得太阳电池在不同环境及环境变化时的I-V、P-V输出特性曲线，数学模型和仿真结果可以反映出太阳电池各项参数的变化规律。太阳电池的仿真模型如图3所示。

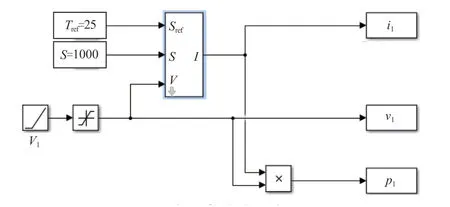
图3 太阳电池的仿真模型Fig. 3 Simulation model of solar cell

1.3 太阳电池的输出特性分析

建立太阳电池仿真模型后，观察并分析太阳电池的输出特性。

将太阳电池仿真模型中的太阳辐照度S设置为1000 W/m2，对太阳电池工作温度Sref分别为25、35、45 ℃时太阳电池的P-V输出特性进行仿真模拟，得到的结果如图4所示。

通过图4中太阳电池的P-V输出特性曲线可知，在太阳电池未达到最大功率点时，其P-V输出特性曲线近似一条有斜率的直线，输出功率随电压的升高而升高；而当太阳电池达到最大功率点之后，随着电压的升高，其输出功率迅速下降。

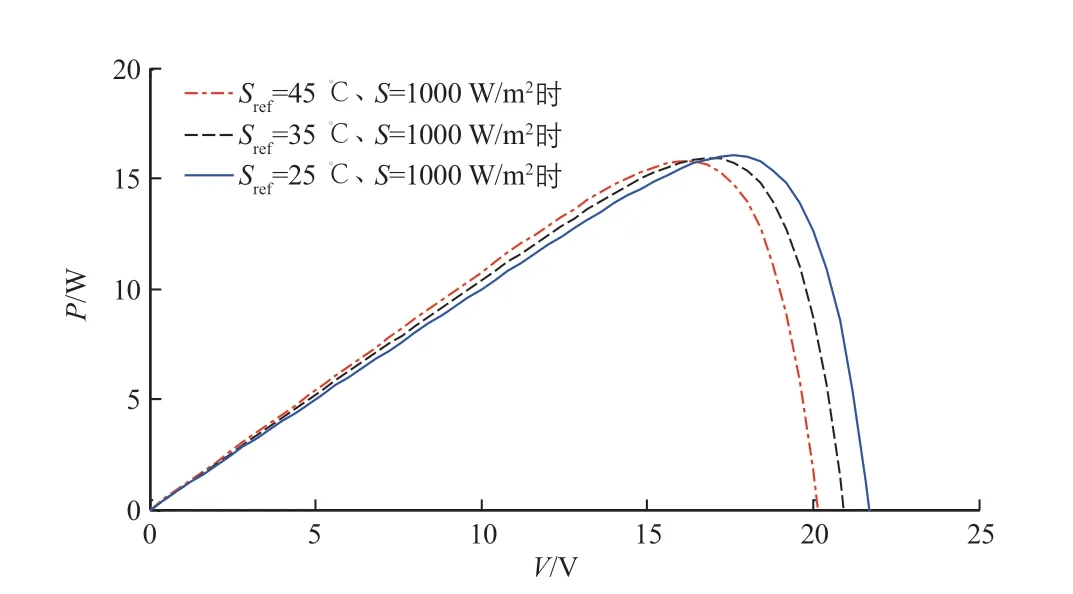
图4 太阳辐照度为1000 W/m2，工作温度分别为25、35、45 ℃时太阳电池的P-V输出特性曲线Fig. 4 P-V output characteristic curves of solar cell when solar irradiance intensity is 1000 W/m2 and working temperature is 25, 35 and 45 ℃ respectively

2 自适应抗扰控制器设计

在本文的MPPT控制算法分析中，MPPT控制的本质就是改变占空比D，进而改变脉冲宽度调制(PWM)波形，利用Boost电路实现阻抗匹配，最终得到太阳电池的最大输出功率[6]。因此，控制D的取值是本文研究的关键和重要依据。基于此，本文设计了一种自适应抗扰控制策略，采用自适应抗扰控制器。

自适应抗扰控制器的设计思路是在模型参考自适应控制器(MRAC)与自抗扰控制器(ADRC)的设计基础上，融合这2种控制器各自的优点而得到的。在自适应抗扰控制器的整体结构中，采用ESO观测太阳电池的电流、电压、功率等状态变量，设定电路阻抗匹配值，与参考模型求误差，根据MRAC的特性设计自适应控制律，消除状态误差，使被控制对象的状态性能与参考模型趋于一致[7]。

自适应控制器模型如图5所示。图中：xp为被控对象的状态量；u为控制输入量；xm为参考模型的状态量；r为设定输入量；e为状态误差；F为状态反馈控制器的状态反馈；K1为状态反馈控制器的增益。

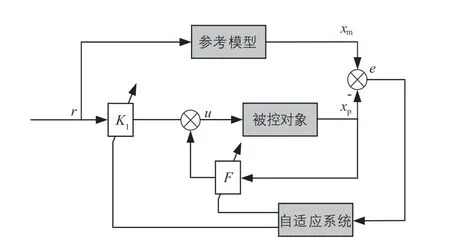
图5 MRAC模型Fig. 5 MRAC model

考虑被控对象的特性和干扰因素，设计合理的自适应控制律成为保证自适应抗扰控制器控制效果的关键。为了保证太阳电池的稳定，本文以李雅普诺夫(Lyapunov)函数作为判别太阳电池稳态的方法，由于该函数具有普遍性和实用性，因此可根据不同阶次的状态方程和Lyapunov函数设计自适应控制律，从而保证太阳电池实现动态响应快、鲁棒性强和抗扰能力强的效果。

考虑太阳电池为二阶非线性系统，设定其中状态变量可观，则太阳电池的空间方程可表示为：

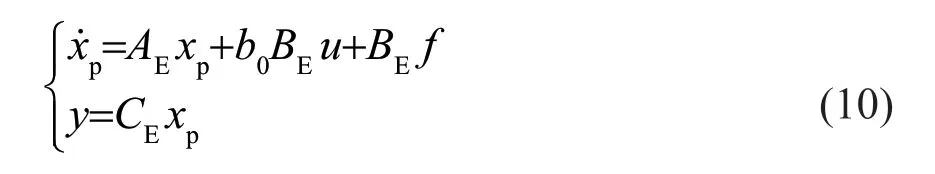
式中：AE、BE、CE均为矩阵；为被控对象的扩张状态量；b0为外部扰动量；f为控制系统的扰动量；y为输出量。

给定太阳电池的参考模型的状态空间方程为：

MRAC的调节过程为：给定信号r并作用于太阳电池和太阳电池参考模型的初始输入端，则太阳电池的响应输出中的状态误差=可表示为：

MRAC的控制系统根据太阳电池特性设计自适应控制律，实时调整太阳电池的参数，即状态反馈控制器的F和K1，保证控制系统实际的响应输出信号与理想的响应输出信号之间的误差趋向于零[8]，即：

式中：t为时间，s。

ADRC根据太阳电池仿真模型的不确定性和非线性等扰动因素，将这些影响控制效果的扰动因素作为其控制系统的总扰动，由ESO进行控制系统变量的观测和补偿，使控制系统变为串联积分结构，最后设计极点配置方式对响应输出信号完成良好的跟踪效果[9]。ADRC模型如图6所示。图中：d为扰动；Z为ESO的状态量；n为状态个数。

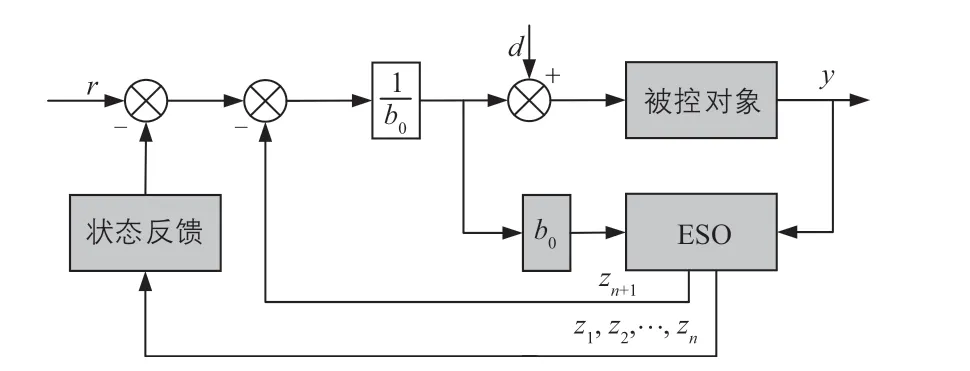
图6 ADRC模型Fig. 6 ADRC model

太阳电池是一种典型的非线性系统，在工作过程中受到环境温度、太阳辐射强度的影响，会使模型参数发生改变，因此传统的控制器难以达到较高的控制精度[10]。MRAC在模型参数不确定的情况下能够自动调整自适应控制律，使被控对象的输出趋近于参考模型的响应输出，具有稳定性好、响应时间快等优点；ADRC能够实现被控对象扰动的主动抑制，引入ESO完成太阳电池的电流、电压和功率信号的观测，使太阳电池的非线性特性具有鲁棒性强、抗扰性好等优点[11]。基于以上，自适应抗扰控制器是以ADRC作为内环结构，MRAC作为外环结构，并将2种控制器各自的优点相互结合而设计成的新型控制器。自适应抗扰控制器模型如图7所示。

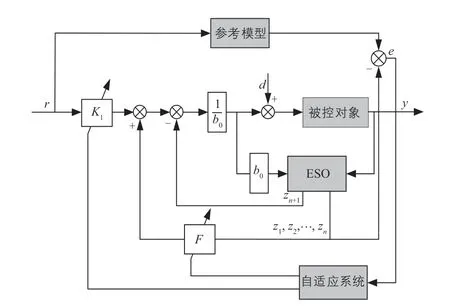
图7 自适应抗扰控制器模型Fig. 7 Adaptive disturbance rejection controller model

3 MPPT仿真结果分析

在MATLAB/Simulink仿真环境中，针对不同情况的环境变化对4种不同的控制策略进行仿真模拟，并对不同控制策略下太阳电池的输出功率和占空比D进行比较。4种控制策略分别为：纯积分控制、PID控制、自适应抗扰控制、固定步长控制。

将环境温度设置为25℃，当太阳辐照度在0.10 s中从1000 W/m2降到800 W/m2时，对4种不同控制策略下的MPPT仿真结果进行分析。4种控制策略下的MPPT仿真波形如图8所示。

图8 4种控制策略下的MPPT仿真波形图Fig. 8 MPPT simulation waveform under four control algorithms

从图8可以看出，综合响应时间、超调量和稳定性等方面，4种控制策略下的MPPT仿真波形中，自适应抗扰控制策略针对太阳电池MPPT具有响应时间快、鲁棒性强和无静态误差等优点，控制效果更好，MPPT控制策略更优。

4 结论

本文为了提高光伏发电系统的发电效率，提出了一种自适应抗扰控制策略，通过对太阳电池的等效电路进行分析并建立太阳电池数学模型，完成了太阳电池的模型仿真，并通过仿真得到了太阳电池的I-V、P-V输出特性曲线。在考虑了太阳电池的最大功率点影响因素(太阳电池工作温度和太阳辐照度等)后，根据太阳电池的特性设计了自适应抗扰控制策略，并通过对4种控制策略进行实验仿真对比，发现本文提出的自适应抗扰控制策略针对太阳电池MPPT具有响应时间快、鲁棒性强和无静态误差等优点。