超燃冲压动力高超声速飞行器巡航弹道分析

张 帆，张会强

(清华大学航天航空学院，北京 100084)

超燃冲压动力高超声速飞行器巡航弹道分析

张 帆，张会强

(清华大学航天航空学院，北京 100084)

在确定的高超声速飞行器几何约束下，建立飞行器气动特性和动力特性随飞行状态变化的耦合计算模型。以最大航程为目标，对超燃冲压动力高超声速飞行器定高和跳跃两种巡航方式的飞行特性进行研究。研究表明：在相同初始和最终状态下，与定高巡航相比，跳跃式巡航能够增加18.5%的航程和 11.5%的飞行时间。定高巡航中飞行器很快由其初始状态过渡到升力-重力和推力-阻力平衡的近似等速飞行状态，而在跳跃式巡航中，飞行器是通过改变飞行高度来动态维持升力-重力平衡的，使其飞行高度明显高于定高巡航。较高的飞行高度使得跳跃巡航所受阻力较小，从而需用推力较小，燃料消耗也较慢，使飞行器能有更长的航程和飞行时间。

高超声速飞行器；耦合；超燃冲压；定高巡航；跳跃式巡航

0 引 言

高超声速飞行器的飞行方式主要有弹道式飞行、高超声速推进滑翔飞行、高超声速定高巡航飞行和高超声速跳跃式巡航飞行等[1-3]。后两者飞行过程主要由助推段、高超声速巡航段和滑翔降落段组成，其中巡航段为有动力飞行。与前两者飞行相比，高超声速动力巡航飞行有更好的机动性能和更大的航程[4]。对高超声速飞行器，可用的动力有火箭发动机或者超燃冲压发动机。相比于火箭发动机，超燃冲压发动机能够利用大气中的氧，比冲较高，更适合作为大气层内高超声速飞行器的动力[5-6]。自20世纪50年代起，针对超燃冲压发动机已开展了大量研究并取得了突破，其已成为可实现和可获得的动力技术[7]，使得超燃冲压动力高超声速飞行器成为可能。

超燃冲压动力高超声速飞行器与发动机高度融合。发动机进气道、隔离段及尾喷管等结构尺寸取决于飞行器的几何构型，而发动机在不同结构尺寸下将有不同的性能，并且飞行器的大小也决定了其所载燃料的多少。同时，超燃冲压发动机属于吸气式动力，其性能受飞行状态影响较大，不同飞行高度和飞行马赫数下具有不同的性能。而发动机性能又将影响飞行器飞行状态。因此，超燃冲压动力高超声速飞行器气动特性、动力特性与飞行状态之间存在强烈的耦合作用。目前针对超燃冲压动力高超声速飞行器巡航阶段的研究中，较少考虑这一耦合作用[2,8]。文献[9-10]虽然考虑了飞行器动力特性与飞行状态之间的耦合，但未考虑文中飞行器几何构型对推进系统性能的约束，与此同时，也未考虑飞行器大小对所载燃料的限制，有一定的局限。

因此，本文基于美国X- 43A飞行器给出了高超声速飞行器的几何构型，在确定的几何约束下建立了飞行器气动特性和动力特性随飞行状态变化的耦合计算模型，以最大航程为优化目标，研究了超燃冲压动力高超声速飞行器定高和跳跃两种巡航方式的飞行特性。

1 计算模型

1.1 飞行器几何特征与气动性能

本文所考虑的高超声速飞行器采用美国X- 43A升力体气动外型[11-12]，气动面积取为180 m2，其几何构型如图1所示。进一步可得到飞行器体积为234 m3，发动机进气道入口截面积为8.8 m2，尾喷管出口截面积为31 m2。飞行器的气动特性如图2所示，其和气动面积决定了飞行器在相应飞行状态下的气动升力和阻力。在飞行器几何尺寸中，气动面积决定了飞行器所受气动升力和阻力，而体积决定了飞行器可携带的燃料量，进气道入口面积和尾喷管出口面积则决定了发动机的推进性能。本文高超声速飞行器的超燃冲压发动机以液氢为燃料，设定飞行器总体积的90%用于载液氢，则可携带15 t液氢。飞行器巡航初始总质量设为40 t，飞行器结构质量20 t，有效载荷质量5 t。因此，本文气动特性、动力特性和载荷特性是在确定的飞行器几何特征约束下实现的。

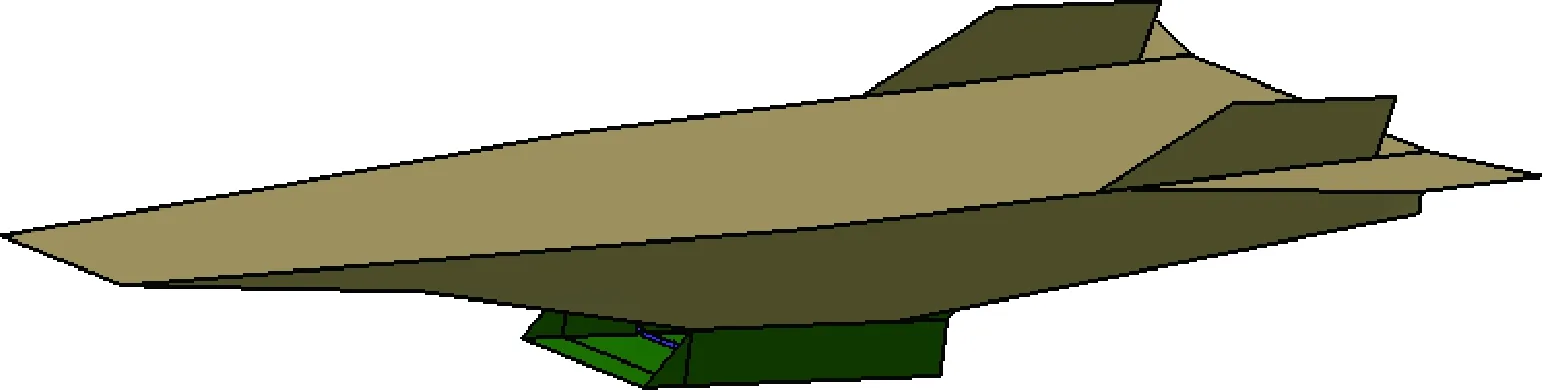
图1 飞行器几何构型Fig.1 Geometry of hypersonic vehicle

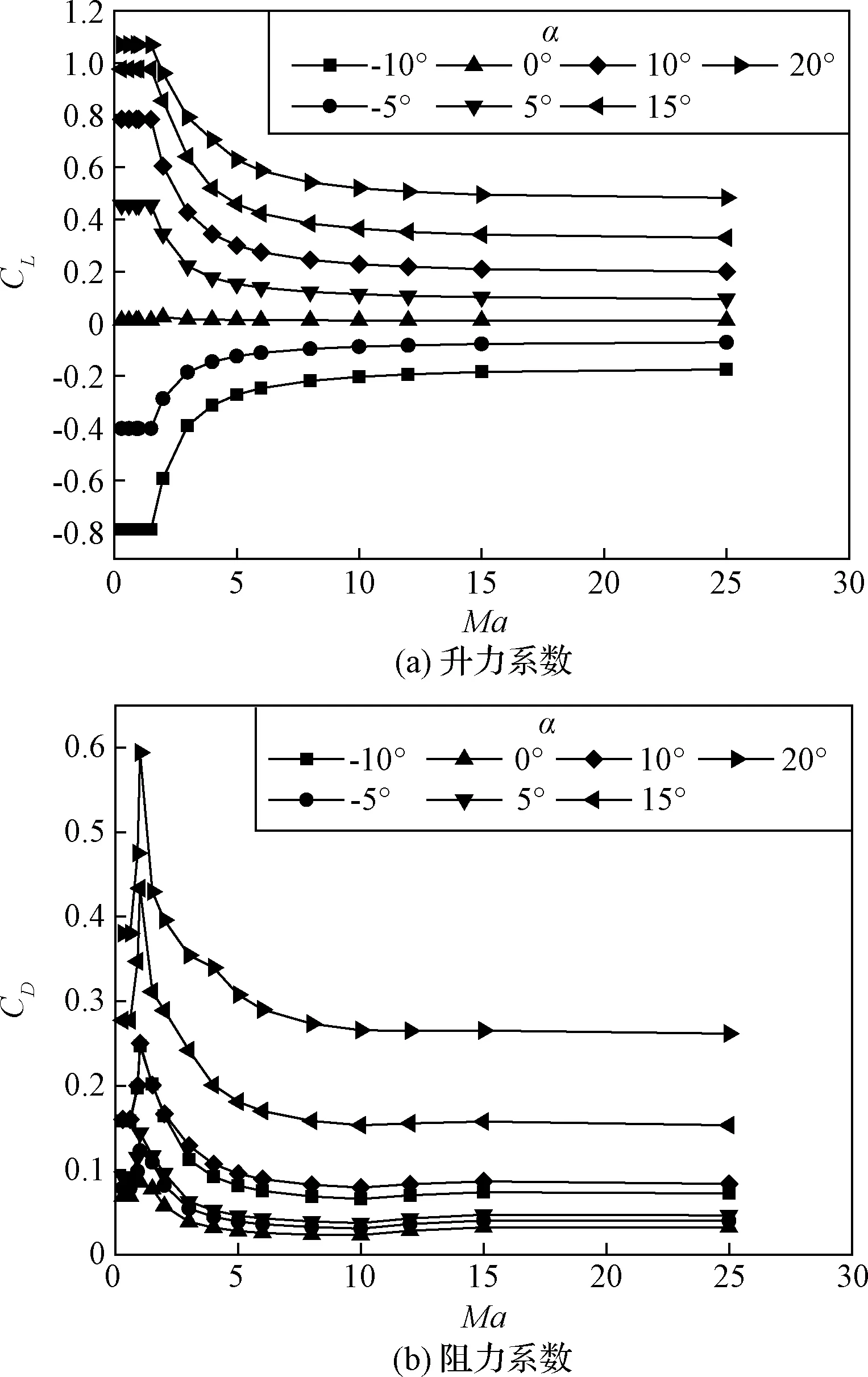
图2 飞行器气动特性Fig.2 Aerodynamic characteristic of hypersonic vehicle

1.2 超燃冲压发动机性能计算

由于实验和数值模拟难度很大，沿飞行弹道超燃冲压发动机整体性能通常采用准一维或热力循环分析方法进行计算[13-14]。本节通过热力循环方法，忽略内流道摩擦力的影响，对基于第1.1节飞行器几何约束的氢燃料超燃冲压发动机进气道压缩、燃烧室加热和尾喷管膨胀三个过程进行分析，得到发动机的推力和比冲性能。

1)圧缩过程。通过进气道压缩将自由流转变为具有一定马赫数(超声速)的燃烧室入口流，气流压缩过程由于激波存在，伴随着一定的总压损失[15]。

2)燃烧过程。燃烧室中发生的是等压燃烧过程[13]。假定燃烧为当量比燃烧，可以计算得到燃烧室出口参数。同时，本文中燃烧室出口静温限制为3000 K，如果以上计算中燃烧室出口静温达到3000 K，燃烧将由当量比燃烧转为贫燃燃烧，由燃烧室出口静温反推得到所需燃料流量。

3)膨胀过程。假定喷管处于最佳膨胀状态(喷管几何结构可调，但不能超出飞行器最大出口面积限制)，可以得到喷管出口参数。如果计算得到的喷管出口面积大于飞行器最大出口面积限制，则喷管处于欠膨胀状态，由最大出口面积反推得到喷管出口压力。

基于以上计算，把超燃冲压发动机在第1.1节确定的几何约束下可实现的推力称之为可用推力FA，如下所示:

(1)

比冲为

(2)

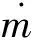
(3)

式中：ρ0和v0分别为来流密度和速度，A0为进气道入口面积，由此可见，在一定飞行状态下，发动机进气量取决于第1.1节中得到的进气道入口截面积。v10代表发动机排气速度，P10代表排气压力，这两个参数取决于尾喷管中气流的膨胀状态。另外，f为燃料-氧化剂比，P0为来流静压，g0为海平面重力加速度。

本文中，燃烧室入口马赫数取值为2～3(对应来流马赫数6～10)，氢燃料热值为119.954 MJ/kg。进气道、燃烧室和尾喷管中定压比热容取值分别为1009 J/(kg·K)、1510 J/(kg·K)和1510 J/(kg·K)；比热比取值分别为1.4，1.238和1.238；气体常数取值均为286.69 J/(kg·K)[16]。

图3为超燃冲压发动机在一定高度(25～60 km)和来流马赫数(6～10)范围内的性能。发动机可用推力随马赫数先增加后降低，原因在于在达到最大值之前，燃烧室出口温度并未达到3000 K，而随后燃烧室出口温度达到3000 K，燃烧由当量比燃烧转为贫燃燃烧，加热量减少，导致可用推力下降。由于大气密度从低到高变化很大，可用推力在不同高度也有较大的变化。发动机比冲随马赫数降低，但在不同高度差异相对较小。比冲曲线特别是低高度比冲曲线中会出现数值突然剧烈下降，也是由于燃烧由当量比燃烧转为贫燃燃烧。

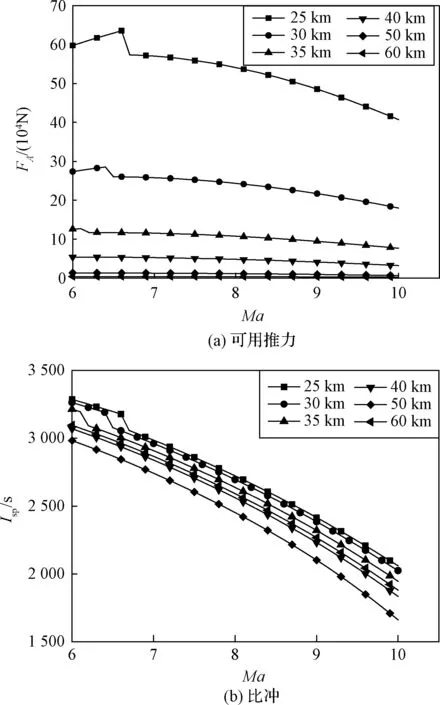
图3 超燃冲压发动机性能Fig.3 Performance of scramjet engine

可用推力FA表示超燃冲压发动机在理想情况下能够产生的最大推力，飞行器飞行过程中发动机推力F可根据飞行情况调节大小，不一定一直处于最大推力状态。本文中定义推力控制系数τ来调节发动机推力输出大小，则

F=τFA

(4)

1.3 飞行器飞行动力学模型

本文中，飞行器由助推火箭加速至高超声速(Ma10)和一定高度(35 km)后助推火箭分离，飞行器以超燃冲压发动机为动力进行定高和跳跃式高超声速巡航。飞行器巡航过程计算中，采用如下假定：地球视为均质圆球，且忽略地球自转；飞行器视为质点；飞行器始终在赤道平面内飞行。飞行动力学方程如下

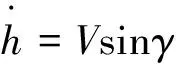
(5)

(6)

(7)

(8)

(9)

式中：FA和Isp分别为动力系统可用推力和比冲，取值基于第1.2节超燃冲压发动机性能计算结果。L和D分别为飞行器的升力和阻力，基于飞行状态由第1.1节的气动特性来确定。h、V、θ、γ和m分别为飞行器飞行高度、飞行速度、经度、弹道倾角和质量，是动力学方程中的状态参数。α为攻角，用来控制飞行器飞行方向，它和推力控制系数τ是动力学方程中的控制参数。t为飞行时间，μ为地球引力常数，r为飞行器到地心距离(地球半径与飞行器高度之和)。

1.4 飞行过程的约束条件

本节给出飞行器定高和跳跃式高超声速巡航弹道的飞行过程约束条件。定高和跳跃式高超声速巡航弹道分别称为方案1和方案2。方案1中飞行器保持在35 km巡航，方案2中高度可以在25～60 km范围内变化，其余条件设置相同。初始经度为0°，由于飞行器在赤道平面内飞行，航程S等于经度变化值(弧度)与地球半径乘积，求最大航程即为求最大最终经度值。为保证吸气式超燃冲压发动机能正常工作，攻角变化范围为-5°～20°。发动机一直保持在工作状态，推力输出值可以通过推力控制系数调节，调节范围0～1。另外，飞行过程中为保证冲压发动机能够正常工作且飞行器结构不被破坏，有三个路径约束[2-3]，最大飞行动压q不超过50 kPa，最大法向过载n不超过4，最大驻点热流密度Q不超过600 kW/m2。本文中规定飞行弹道倾角和攻角的逆时针方向为正。两个方案状态参数、控制参数和路径限制参数约束条件如表1所示。

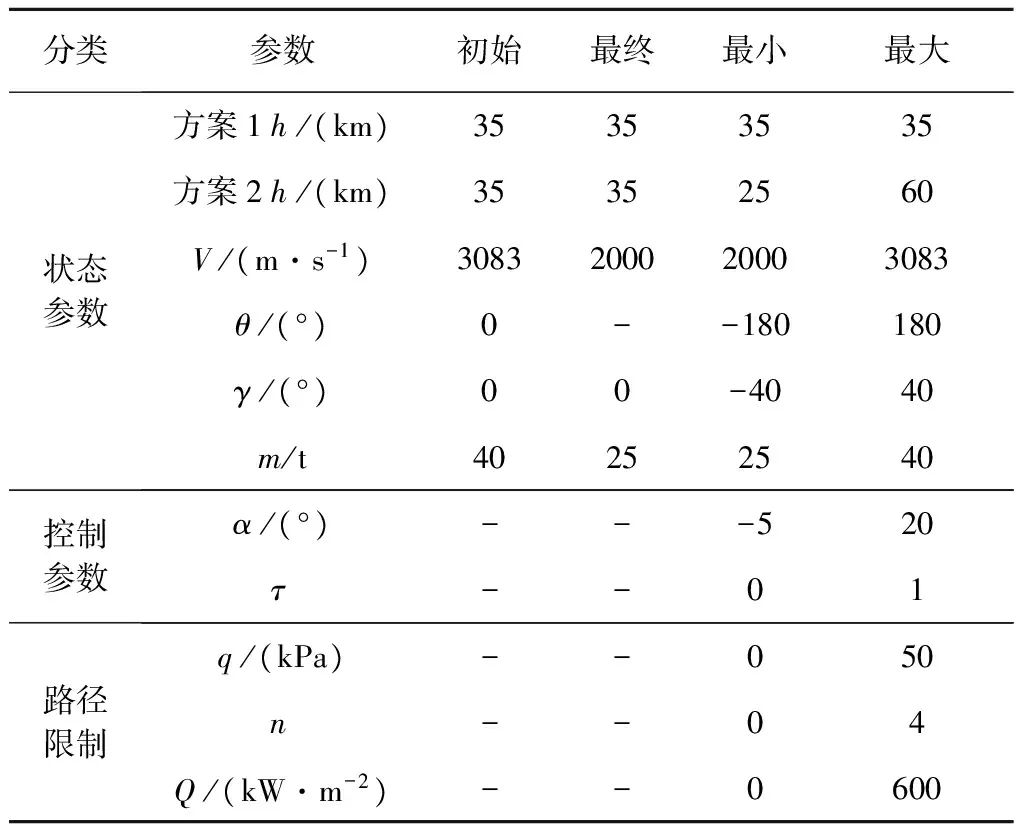
表1 飞行过程约束条件

1.5 弹道优化方法

弹道优化问题本质为最优控制问题，本文以最大航程为优化目标，以攻角和推力控制系数为控制变量，以飞行高度、速度、航程(经度)、弹道倾角和质量为状态变量，同时考虑第1.4节中飞行过程约束条件，对飞行器定高和跳跃式高超声速巡航弹道进行优化。采用hp自适应Radau伪谱法求解该优化问题[9-10,17]。该方法为直接优化算法，将状态变量和控制变量在一系列Legendre-Gauss-Radau配点上离散，并以离散点为节点构造Largrange插值多项式来拟合状态变量和控制变量。通过对全局插值多项式求导来近似状态变量对时间的导数，将运动微分方程转化为一组代数方程，将弹道优化转化为非线性规划问题。同时，该方法采用hp自适应网格重构策略，能以较小的计算代价得到较高精度的解。

2 结果与分析

以马赫数10、高度35 km为飞行器初始状态，消耗完所携带的15 t液氢燃料为终态，方案1飞行时间和航程分别为4626.6 s和9368.9 km，而方案2飞行时间和航程分别为5159.7 s和10648 km。方案2比方案1航程和飞行时间分别增加了1279.1 km和533.1 s，分别为方案1航程和飞行时间的18.5%和 11.5%，可见相对定高巡航，跳跃式巡航能够显著增加航程和飞行时间。

图4和图5分别为两个方案中飞行器控制参数攻角和推力控制系数随时间的变化图。图6～9分别为两个方案中飞行器状态参数高度、速度、马赫数和质量随时间(航程)的变化曲线。图10为两个方案中超燃冲压发动机可用推力和比冲随时间的变化图，而图11为发动机实际推力随时间的变化图。基于这些结果对两个巡航方案进行比较，并分析其航程和飞行时间不同的原因。

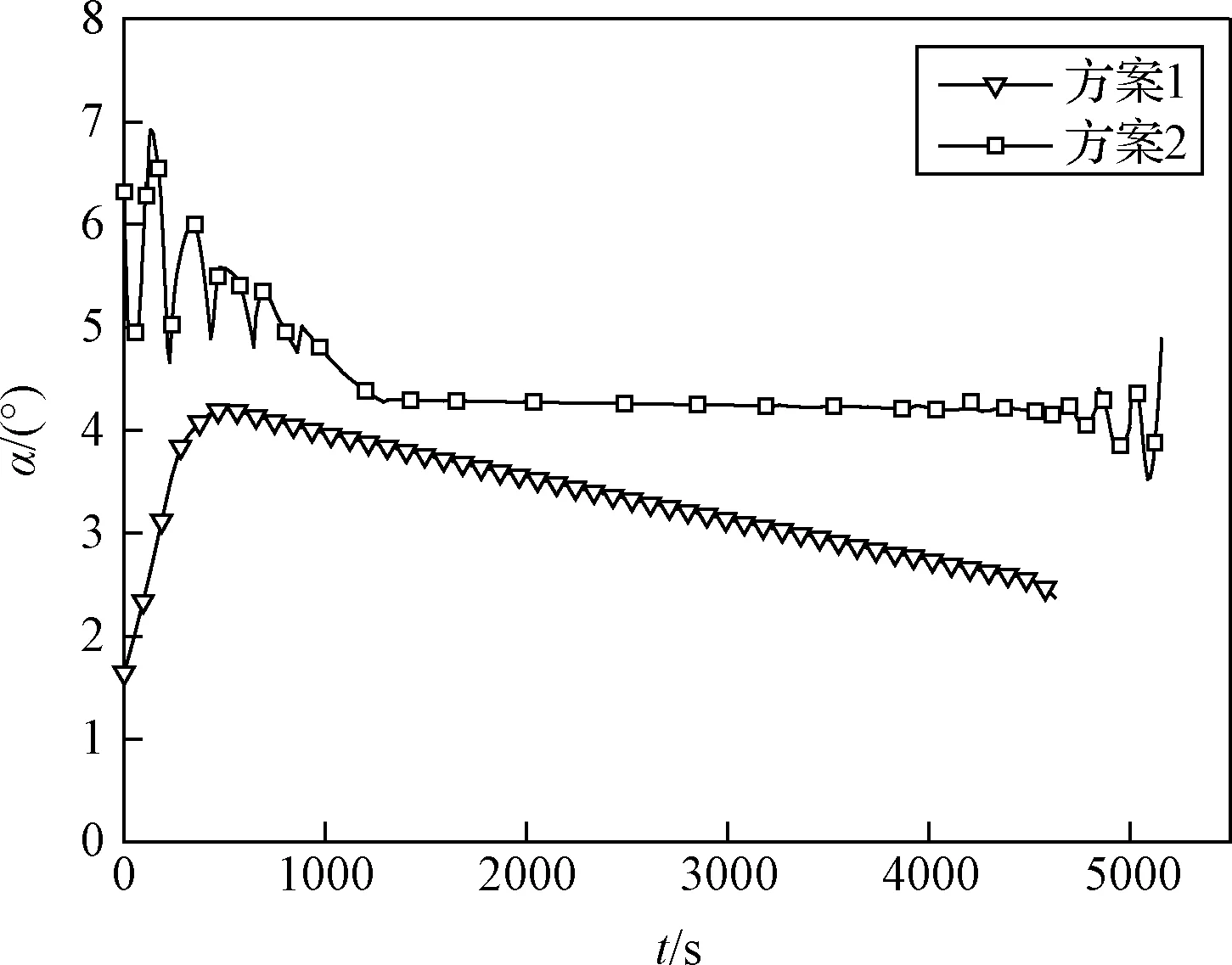
图4 飞行器攻角随飞行时间变化Fig.4 Angel of attack VS time

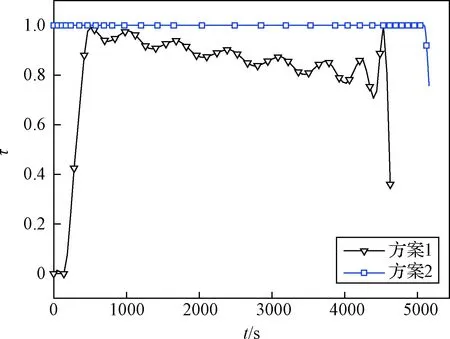
图5 飞行器推力控制系数随飞行时间变化Fig.5 Thrust scaling coefficient VS time

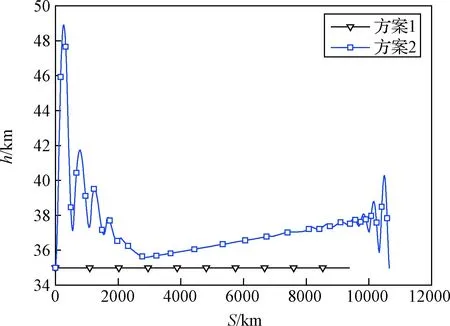
图6 飞行器高度随航程变化Fig.6 Altitude VS range

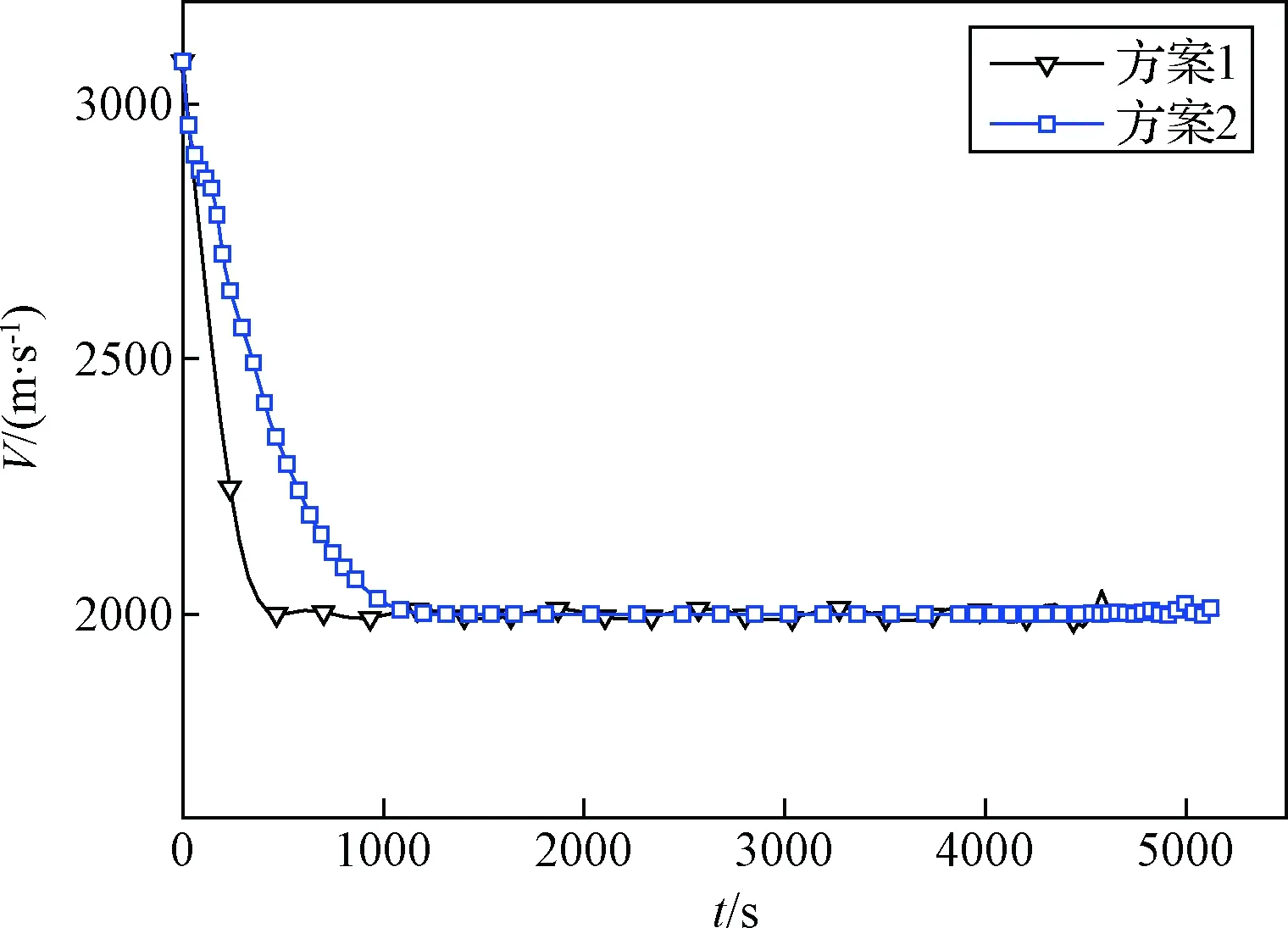
图7 飞行器速度随飞行时间变化Fig.7 Velocity VS time

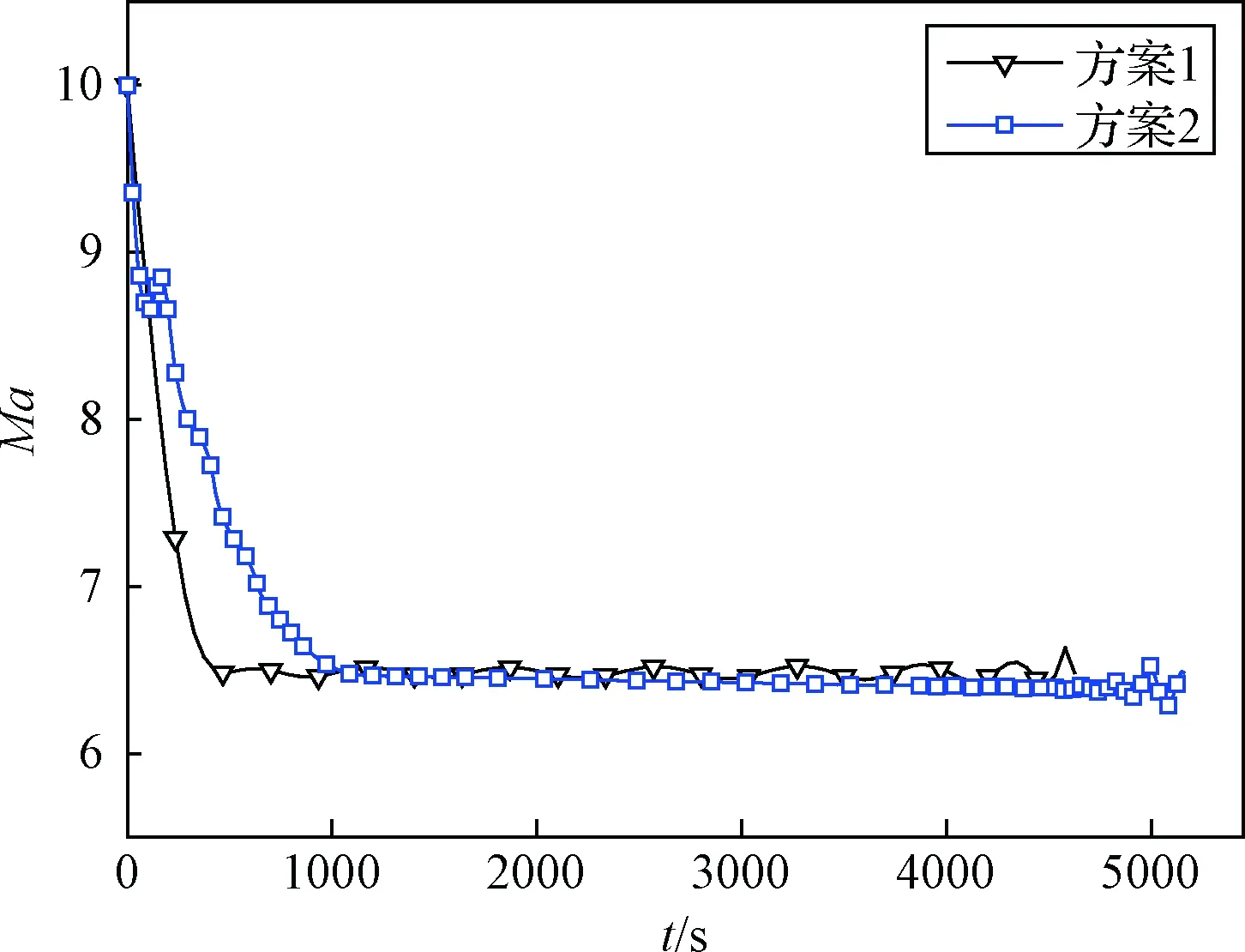
图8 飞行器马赫数随飞行时间变化Fig.8 Mach number VS time

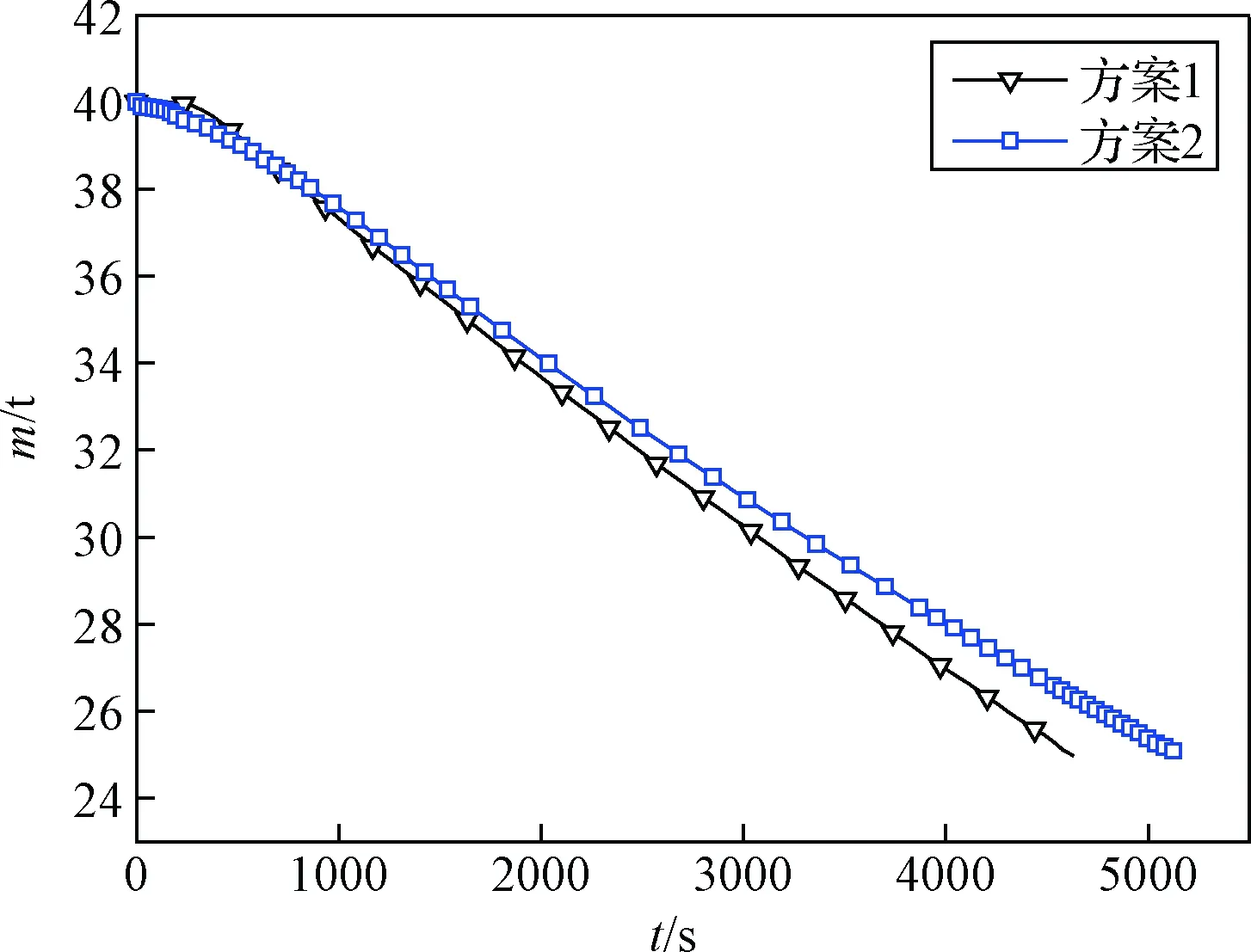
图9 飞行器质量随飞行时间变化Fig.9 Mass VS time

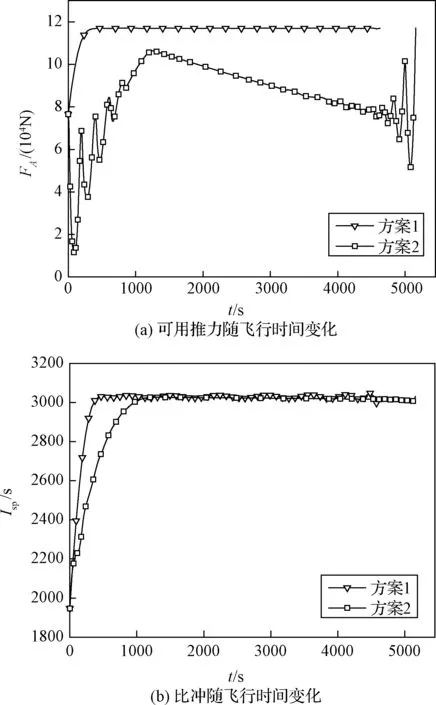
图10 超燃冲压发动机性能随飞行时间变化Fig.10 Scramjet performance VS time

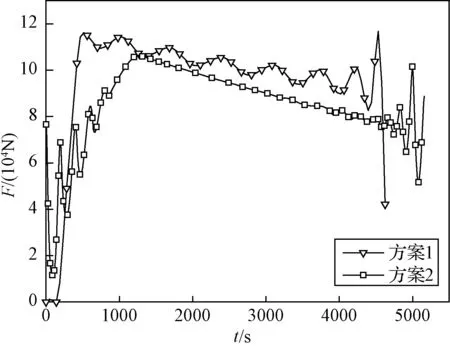
图11 发动机推力随飞行时间变化Fig.11 Thrust of scramjet VS time

1)方案1

整个飞行过程飞行器高度保持在35 km(见图6)。飞行开始之后，由于飞行速度较快，气动阻力比较大，因此飞行速度和马赫数降低(见图7和图8)，飞行速度的降低也有利于减小飞行阻力损失。与此同时，在一定攻角下(见图4)，该阶段气动升力也比较大，足以克服重力，使飞行器在35 km高度飞行。随着飞行速度的降低，气动升力逐渐减小，不足以克服重力，所以发动机推力和攻角逐渐增大(见图4和图11)，增加推力在升力方向的分量以克服重力。速度降低到2000 m/s时，发动机推力和攻角达到一个极值。之后随着燃料消耗飞行器质量减小(见图9)，重量减小，因此发动机推力和攻角又降低，以使飞行器在垂直于速度方向受力平衡。同时，攻角的减小也使推力在速度方向的分量增大，与阻力相平衡。当推力减小到一定程度后，推力在速度方向的分量不足以克服阻力，因此发动机推力又将增大。之后，随着飞行器质量减小，以上飞行过程又将重复，导致发动机推力出现一定波动，直到飞行结束。

在该飞行过程中，飞行前期马赫数从Ma10开始下降，导致超燃冲压发动机可用推力在此阶段增加，如图10(a)所示，这与图3(a)中发动机可用推力性能的变化趋势是一致的，之后，方案1中的可用推力基本保持不变，是因为该阶段高度和马赫数基本保持不变。比冲在飞行前期增加，在飞行后期基本保持不变，如图10(b)所示，这是由于飞行器马赫数先降低后保持不变导致。

2)方案2

整个飞行过程中飞行器高度可在35～50 km范围内变化(见图6)。飞行开始之后，由于飞行速度较快，气动升力较大，同时，在一定攻角下，推力也提供了一个升力方向的分量，这两者合力将飞行器拉起爬升，高度的增加降低了大气密度，导致阻力下降，有利于减小阻力损失。到达一定高度后，大气密度减小将导致升力减小，当前面提到的合力不足以抵消重力时，飞行高度又将下降，进行俯冲飞行，因此出现了高度跳跃。经过几个跳跃之后，飞行器速度降低到2000 m/s，升力也降低，飞行器在垂直于飞行速度方向受力相对平衡，故飞行高度变化在此阶段变化较为平稳。在飞行后期，燃料消耗导致飞行器质量进一步减小，虽然此时升力相对飞行前期要小，但仍足以将飞行器再次拉起爬升，故此阶段也出现了高度跳跃直到飞行结束，但高度变化范围较飞行前期缩小。

在该飞行过程中，超燃冲压发动机可用推力随飞行器高度变化呈波动性变化，如图10(a)所示，在飞行前期，超燃冲压发动机可用推力随马赫数下降在波动中出现整体上升趋势。与可用推力不同，高度的跳跃式变化并没有给发动机比冲变化带来太大影响，如图10(b)所示，是因为超燃冲压发动机比冲在不同高度差异相对较小，如图3(b)所示。

3)方案1与方案2的比较

飞行开始时，若飞行器处于零攻角，两个方案中飞行器推力均小于阻力，升力也不足以克服重力。方案1中飞行器开始时刻采用一定的攻角，使升力增大，用以克服重力，同时通过减速，降低阻力，并很快达到阻力方向和升力方向的受力平衡，直至燃料最终耗尽。方案2中飞行器由于没有35 km高度限制，开始时刻采用较方案1更大的攻角以产生更大升力，同时推力也提供了一个升力方向的分量，这两者合力将飞行器拉起爬升，大的攻角虽然带来了更大的阻力系数，但由于高度下降空气密度减小，方案2飞行器所受阻力小于方案1，故此阶段方案2速度和马赫数下降速度小于方案1(见图7和图8)。另外，由于方案2整个飞行过程中高度均大于35 km，整体所受阻力也要小于方案1，因此，在大部分飞行过程中方案2发动机推力小于方案1，燃料消耗也慢于方案1(见图9)，最终使飞行器能有更长的飞行时间和航程。

3 结 论

本文首先基于美国X- 43A飞行器给出了高超声速飞行器的几何构型，确立了飞行器气动特性、动力特性和载荷特性的几何约束。随后计算得到该约束下氢燃料超燃冲压发动机的性能，并建立了飞行器气动特性和动力特性随飞行状态变化的耦合计算模型。最后采用hp自适应Radau伪谱法，以最大航程为优化目标，对超燃冲压动力高超声速飞行器定高和跳跃两种巡航方式的飞行特性进行了研究和分析。结果表明：在相同初始和最终状态下，与定高巡航相比，跳跃式巡航能够显著增加航程和飞行时间。主要是跳跃式巡航通过改变飞行高度来动态维持升力-重力平衡，可实现较高的飞行高度，使其所受阻力较小。进一步使得需用推力减小，燃料消耗慢，相同的燃料携带量使得跳跃式巡航飞行具有更长的航程和飞行时间。

[1] 王洁瑶, 江涌, 钟世勇, 等. 高超声速远程导弹弹道解析估算与特性分析[J]. 宇航学报, 2016, 37(4): 403-410. [Wang Jie-yao, Jiang Yong, Zhong Shi-yong, et al. Analytical estimation and analysis of trajectory performance for hypersonic long-range missiles[J]. Journal of Astronautics, 2016, 37(4):403-410.]

[2] 易文双. 动力滑翔高超飞行器轨迹设计与射程优化[D]. 哈尔滨: 哈尔滨工业大学, 2014. [Yi Wen-shuang. Trajectory design and range optimization of gliding hypersonic vehicle with powered[D]. Harbin: Harbin Institute of Technology, 2014.]

[3] 赵红. 高超声速飞行器跳跃飞行轨道优化研究[D]. 哈尔滨: 哈尔滨工业大学, 2008. [Zhao Hong. Optimization research of hypersonic vehicle skip flying trajectory[D]. Harbin: Harbin Institute of Technology, 2008.]

[4] Carter P H, Pines D J, Rudd L V. Approximate performance of periodic hypersonic cruise trajectory for global reach[J]. Journal of Aircraft, 1998, 35(6): 857-867.

[5] Tian L, Chen L, Chen Q, et al. Quasi-one-dimensional multimodes analysis for dual-mode scramjet[J]. Journal of Propulsion and Power, 2014, 30(6):1559-1567.

[6] Zhang F, Zhang H, Wang B. Feasibility study of a DRBCC-powered single-stage-to-orbit launch vehicle[C]. The 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, USA, July 25-27, 2016.

[7] Segal C. The scramjet engine: processes and characteristics[M]. Cambridge: Cambridge University Press, 2009.

[8] 赵钧，孟令赛. 高超声速临近空间飞行器跳跃飞行轨迹优化[J]. 战术导弹技术, 2010(5): 32-35. [Zhao Jun, Meng Ling-sai. Jumping trajectory optimization of the near space vehicles with hypersonic speed[J]. Tactical Missile Technology, 2010(5): 32-35.]

[9] 明超, 孙瑞胜, 白宏阳, 等. 吸气式超声速导弹爬升段多约束轨迹优化[J]. 宇航学报, 2016, 37(9): 1063-1071. [Ming Chao, Sun Rui-sheng, Bai Hong-yang, et al. Climb trajectory optimization with multiple constraints for air-breathing supersonic missile[J]. Journal of Astronautics, 2016, 37(9):1063-1071.]

[10] Chai D, Fang Y, Wu Y, et al. Boost-skipping trajectory optimization for air-breathing hypersonic missile[J]. Aerospace

Science and Technology, 2015, 46: 506-513.

[11] Marshall L A, Corpening G P, Sherrill R. A chief’s view of the NASA X- 43A scramjet flight test[C]. The 13th AIAA International Space Planes and Hypersonic Systems and Technology Conference, Capua, Italy, May 16-20, 2005.

[12] Morelli E A, Derry S D, Smith M S. Aerodynamic parameter estimation for the X- 43A (Hyper-X) from flight data[C].AIAA Atmosphere Flight Mechanics Conference and Exhibit, San Francisco, USA, August 15-18, 2005.

[13] Yang Q, Chang J, Bao W. Thermodynamic analysis on specific thrust of the hydrocarbon fuel scramjet[J]. Energy, 2014, 76:552-558.

[14] Roux J A. Parametric ideal scramjet cycle analysis[J]. Journal of Thermophysics and Heat Transfer, 2011, 25(4): 581-585.

[15] 吕翔. 火箭基组合循环(RBCC)发动机性能分析模型研究[D]. 西安:西北工业大学, 2005. [Lv Xiang.Study on performance analysis model of rocker-based-combined-cycle (RBCC) Engine[D]. Xi’an: Northwestern Polytechnical University, 2005.]

[16] 郑小梅, 徐大军, 蔡国飙. 超燃冲压发动机性能的初步分析[J]. 宇航学报, 2007, 28(S): 36-41. [Zheng Xiao-mei, Xu Da-jun, Cai Guo-biao. A preliminary study on hypersonic airbreathing engine performance[J]. Journal of Astronautics, 2007, 28(S): 36-41.]

[17] Garg D, Patterson M A, Darby C L, et al. Direct trajectory optimization and costate estimation of finite-horizon and infinite-horizon optimal control problems using a Radau pseudo-spectral method[J]. Computational Optimization and Applications, 2011, 49(2): 335-358.

通信地址：北京市海淀区清华大学蒙民伟科技大楼北楼(100084)

电话：13811185389

E-mail: zfhappy1989@163.com

张会强(1966-)，男，博士，教授，主要从事湍流两相流动与燃烧等相关的基础研究，以及面向火箭发动机、航空发动机、冲压发动机及组合动力的应用研究。本文通信作者。

通信地址：北京市海淀区清华大学蒙民伟科技大楼北楼(100084)

电话：(010)62772917

E-mail: zhanghq@mail.tsinghua.edu.cn

Cruise Trajectory Analysis of Scramjet-Powered Hypersonic Vehicle

ZHANG Fan, ZHANG Hui-qiang

(School of Aerospace Engineering, Tsinghua University, Beijing 100084, China)

The cruise trajectory model of a hypersonic vehicle, which couples the vehicle’s aerodynamic characteristics, propulsion characteristics and flying conditions, is established under the certain geometry constrains. Then the scramjet-powered cruise trajectories of the fixed-altitude flight and skipping flight are analyzed subject to maximizing the flight range. Results show that the skipping flight has the advance to fixed-altitude flight on flight range by 18.5%, and the flight time increases by 15.5%. In fixed-altitude flight, the vehicle quickly transits from the initial state to a quasi-constant-velocity state, in which the lift-gravity force and thrust-drag force are both in balance. In skipping flight, the lift and gravity force keep in balance through changing flight altitude. This makes the flight altitude in skipping flight is higher than fixed-altitude flight and the drag force is relatively smaller, then the thrust force and fuel consumption rate in skipping flight is less than fixed-altitude flight, which leads to the longer flight range and flight time in skipping flight.

Hypersonic vehicle; Couple; Scramjet; Fixed-altitude flight; Skipping flight

2017- 03-27;

2017- 06- 05

V412

A

1000-1328(2017)08- 0797- 07

10.3873/j.issn.1000-1328.2017.08.003

张 帆(1989-)，男，博士生，主要从事组合动力及高超声速飞行器技术研究。