含LESO的高超声速飞行器动态面控制
2017-09-12杨文骏
杨文骏,张 科,王 佩
(1. 航天飞行动力学技术重点实验室,西安 710072;2. 西北工业大学航天学院,西安 710072)
含LESO的高超声速飞行器动态面控制
杨文骏1,2,张 科1,2,王 佩1,2
(1. 航天飞行动力学技术重点实验室,西安 710072;2. 西北工业大学航天学院,西安 710072)
针对含模型不确定性和外部扰动的高超声速飞行器(HFV)巡航飞行的控制问题,提出一种基于线性扩张状态观测器(LESO)的动态面控制方法。首先,建立高超声速飞行器的纵向运动模型,并采用非线性动态逆(NDI)技术实现了飞行器速度和高度通道的解耦;其次结合传统反演设计方法,采用基于反双曲正弦函数的跟踪微分器(IHSTD)求取虚拟控制量的微分信号,避免了“微分爆炸”的问题;然后设计了LESO,能够实现对模型不确定项和外部扰动组成的“总和扰动”的精确估计,进而在控制器中动态补偿,大幅增强了系统的扰动抑制能力;最后,采用Lyapunov稳定性理论对所提出的控制方法进行了稳定性分析。本文所提出的控制方法保证了系统的渐近稳定性和较强的鲁棒性,仿真结果校验了本文所设计控制器的有效性。
高超声速飞行器(HFV);跟踪微分器;线性扩张状态观测器(LESO);扰动抑制;动态面控制;鲁棒性
0 引 言
高超声速飞行器(Hypersonic flight vehicle, HFV)指的是可以在临近空间以Ma5以上的速度飞行的一类飞行器[1]。因其具有快速响应、机动性强和突防能力强等优点,并具备全球打击能力,故吸引了许多国家及科研机构对其开展研究。但HFV具有强非线性、强耦合和模型不确定等特点,且易受外界干扰,这给HFV的控制系统设计带来了极大的挑战[2]。
近年来,随着控制技术的发展和研究的深入,HFV的控制系统设计取得了显著成效。各类控制方法如增益预置[3]、线性变参控制[4]、鲁棒控制[5]和反演控制[6]等,都在HFV的控制系统设计中得到了应用。反演控制方法是处理系统非匹配不确定性和实现多变量解耦控制的一种重要非线性控制方法,而干扰观测器能实现对不确定性及各类扰动的有效估计,并在控制器中实现前馈补偿。文献[6]针对含不确定干扰项的高超声速飞行器模型,设计了基于指令滤波器的反演控制方法,实现了对速度和航迹角指令的稳定跟踪。Wu等[7]提出了基于非线性扰动观测器的鲁棒反演控制,在飞行器含有参数不确定的影响下,取得了良好的控制效果。文献[8]提出了近似反演容错控制方法,解决了含参数不确定、外部扰动和执行器故障的飞行器飞行控制问题。文献[9]针对高超声速飞行器非线性动力学系统具有不确定项的问题,设计了一种自适应反演控制器。文献[10]提出了一种基于神经网络逼近的新型反演控制方法,采用神经网络来逼近系统的不确定项,保证了速度和高度良好的指令跟踪效果。
扩张状态观测器是自抗扰控制技术[11]的核心部分,其特点是不需精确的模型信息就能实现对系统不确定项、未建模动态和外部扰动等组成的“总和扰动”的有效估计。针对高超声速飞行器复杂非线性和高不确定性等特点,文献[12]提出了基于扩张状态观测器的动态逆设计方法,并将其应用于飞行器的三通道姿态控制中。文献[13]针对含参数不确定性和外部扰动等问题高超声速飞行器巡航飞行控制,提出了一种基于扩张状态观测器的非线性动态逆控制方法。近年来,相关学者[14-17]在扩张状态观测器、自抗扰控制器的收敛性的严格理论证明方面做了大量工作。文献[14]给出了自抗扰控制技术应用于一类含较大不确定性的MIMO非线性系统的全局和半全局收敛性的严格证明。文献[15]将含扩张状态观测器的目标系统的误差动态方程转换为一个具有小扰动的渐近稳定系统,并给出了扩张状态观测器收敛性的严格证明。文献[16]基于扩张状态观测器和投影梯度估计器设计了输出反馈控制器,使得具有零动态的一类仿射非线性不确定动态系统能够稳定跟踪给定的指令信号。文献[17]采用自抗扰控制技术,研究了一类具有执行器饱和问题的非线性系统在系统状态部分可测和系统非线性动态大量未知的情况下的镇定问题。
传统反演法的突出问题是随着系统阶数的增加,需要求取虚拟控制量的高阶微分信号,导致“微分项爆炸”的问题。常用的解决方法是引入动态面控制技术,一般采用一阶低通滤波器(Low-pass filter, LPF)来求取虚拟控制量及其微分信号,但其对噪声的抑制能力不强。文献[18]提出的基于反双曲正弦函数的跟踪微分器(IHSTD),能够高精度地跟踪输入信号,且响应快,并能较好地抑制微分信号的噪声放大效应。
Gao[19]基于自抗扰控制技术,提出了线性扩张状态观测器(Linear extended state observer, LESO),采用带宽的概念确定其参数,相比于扩张状态观测器,结构设计更为简便,所需调节参数少。
注意到,上述部分研究成果存在仅考虑不确定项的影响,算法复杂、参数设置繁琐和未考虑滤波误差等问题。本文针对含模型不确定项和外部扰动的高超声速飞行器纵向模型,设计了含LESO的非线性动态面控制器。结合传统反演法和动态面控制技术,采用IHSTD求取虚拟控制量的微分信号,避免了“微分爆炸”的问题,并在综合稳定性分析中考虑了滤波误差的影响;结合模型精确反馈线性化过程中的部分信息,设计了简单的二阶LESO,实现对系统总和扰动的精确估计和补偿;最后通过仿真实例校验了所设计控制策略的有效性。
1 模型及问题描述
1.1 HFV纵向模型
考虑HFV的纵向模型
(1)
式中:V,γ,H,α,q分别为HFV的速度、航迹角、高度、攻角和俯仰角速率;μ为地心引力常数;r是HFV到地心的距离,r=RE+H,RE为地球半径;M和Iyy分别为HFV的质量及其沿y轴的转动惯量;L,D,T,Myy分别为HFV的升力,阻力,推力及俯仰力矩。各参数的具体表达式可参照文献[13]。
简化的发动机模型采用一个二阶系统描述
(2)
式中:ξ,ωn分别为二阶系统的阻尼比和自然频率;β,βc分别表示发动机节流阀的实际开度及其指令值。
(3)
式中:FV,FH和B的详细表达式参考文献[20]。
假设 1. 矩阵B非奇异。
注1. 考虑到HFV在巡航飞行过程中,航迹角很小,满足γ≠±π/2,所以HFV的飞行航迹不是垂直的,故矩阵B非奇异,假设1成立。
1.2 问题描述
考虑HFV的参数不确定性
(4)
式中:( )0表示参数标称值; Δ()表示参数偏移量。其参数偏移量如下
(5)
将系统的未知动态和外部扰动等视为系统的等效复合扰动,考虑以上情况,系统动态可描述为
(6)
式中:ΔFV,ΔFH和ΔB为系统不确定项;B0表示标称控制矩阵;d1(t)和d2(t)为等效到速度和高度通道的复合扰动。
系统对ΔB的敏感程度要远高于ΔFV和ΔFH,故ΔFV和ΔFH可以忽略不计。因此式(6)可改写为
(7)
将速度和高度通道中的系统不确定性、等效复合扰动视为“总和扰动”
(8)
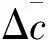
2 含LESO的动态面控制器设计
2.1 IHSTD设计
反双曲正弦函数是光滑连续函数,具有快速并消除速度高频震颤的作用。利用反双曲正弦函数构造加速度函数,设计IHSTD[18]
(9)
式中:r(t)为输入信号;z1(t),z2(t)分别是二阶IHSTD的状态变量;参数R>0,a1>0,a2>0,b1>0,b2>0。
将IHSTD和传统低通滤波器(Low pass filter,LPF)进行对比。LPF的时间常数为0.02,IHSTD的参数设置为R=30,a1=a2=3,b1=b2=1。输入信号分别是r1(t)为典型方波和r2(t)=sin(2πt)的正弦信号,均加入均值为0、方差为0.01的高斯白噪声干扰,对比结果如图1。
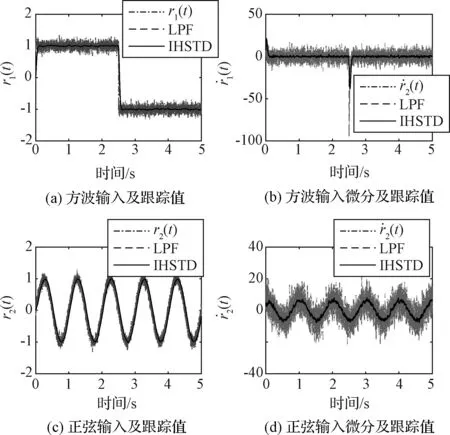
图1 IHSTD和LPF的跟踪效果对比Fig.1 Comparison of the tracking performance between IHSTD and LPF
图1(a)和(b)是IHSTD和LPF对方波输入及其微分信号的跟踪效果,图1(c)和(d)是IHSTD和LPF对正弦输入及其微分信号的跟踪效果。表1为LPF和IHSTD跟踪输入及其微分信号的均方根误差(Root mean square error,RMSE),值越小表示跟踪精度越高。
从图1和表1的对比可以看出,在有噪声干扰的情况下,LPF和IHSTD都能较快且稳定地跟踪上输入信号,两者的性能接近;但对于输入的微分信号的跟踪,IHSTD具有更强的噪声抑制能力,性能明显优于LPF。故在本文的动态面控制器设计中采用IHSTD来求取虚拟控制量的微分信号。
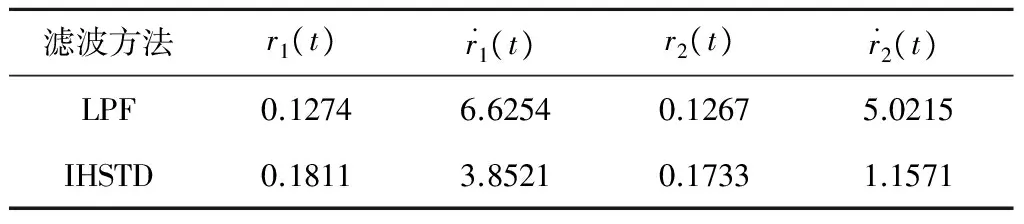
表1 LPF和IHSTD跟踪参考输入的均方根误差
2.2 动态面控制器设计
将式(3)写成紧凑形式
G=F0+Bu
(10)
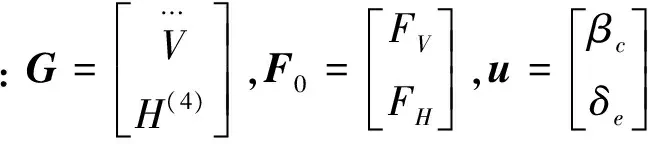
通过结合动态面控制技术的反演法设计得到G,进而得到动态面控制器
(11)
(12)
定义4个误差变量
(13)
式中:χhi(i=1,2,3)为需要设计的虚拟反馈控制量。
式(13)本质上为式(12)的微分同胚,因此镇定式(12),只需镇定式(13)即可。
对Zh1求导,得
(14)
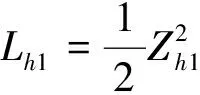
(15)
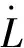
对Zh2求导,得
(16)
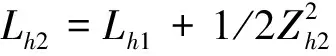
(17)
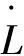
对Zh3求导,得
(18)

(19)
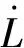
对Zh4求导,得
(20)
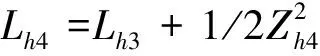
(21)
故Zh1,Zh2,Zh3和Zh4都能收敛到零,这也保证了HFV的高度跟踪误差能稳定收敛到零。得到所需的H(4)如
(22)
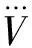
2.3 LESO设计
结合模型精确反馈线性化的部分信息,针对HFV的速度和高度子系统,分别设计简单的二阶LESO对系统的总和扰动进行估计补偿。
(23)
针对系统(23)设计二阶LESO如下
(24)
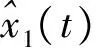
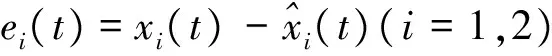

(25)
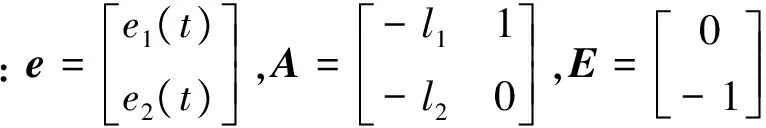
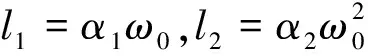
λO(s)=s2+l1s+l2=(s+ωo)2
(26)
只要满足ωo>0,式(26)就具有负实部根,保证了系数矩阵A是Hurwitz稳定的。令ω0=1/ε,则有li=αi/εi,再令gi(e1(t))=αie1(t),式(24)可转换为
(27)
定义
(28)
则系统(27)对系统(23)的观测误差动态可描述为
(29)

注2. 超声速飞行器巡航飞行过程中,其参数不确定性和外部扰动均在一定范围内,故假设2成立。
假设 3. ∀ζ(t)=[ζ1(t),ζ2(t)]T∈R2,存在常数λi(i=1,2,3,4),β以及连续可微、径向无界的正定函数V,W:R2→R,满足如下条件:
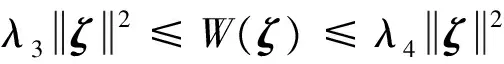
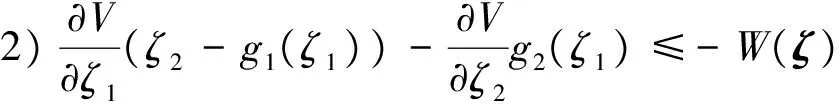
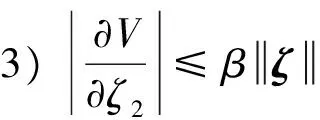
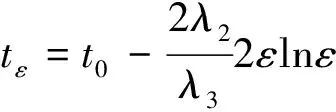
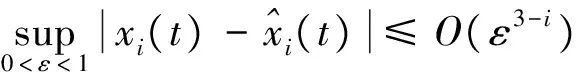
(30)
证. 对Lyapunov函数V(ζ(t))沿系统(29)对时间t求导数
而
则有
故观测误差满足
O(ε3-i), ∀t∈[tε,∞)
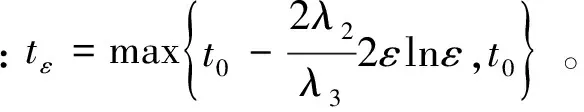
从定理1及其证明过程可以看出,当参数ε取得足够小时,所设计LESO的估计状态能在整个时域上充分逼近系统(23)的状态,且估计误差收敛于O(ε3-i)。同理,将该LESO应用于高度子系统,参数设置不变,可实现对总和扰动的有效估计。结合式(11),最终得到基于LESO的HFV动态面控制器
(31)
2.4 稳定性分析
选取Lyapunov函数为
L=L1+L2+L3
(32)
选择L1为
(33)
对L1求导可得
(34)
定理 2[18]. 系统(9)在原点(0,0)处的渐近稳定性,等价于系统
(35)
在原点(0,0)处的渐近稳定性。式中:参数a1,a2,b1和b2均大于0。
(36)
因为a1>0,b1>0,且反双曲正弦函数与其自变量的符号相同,再由积分中值定理,得
∫z1,hi0a1arsinh(b1δ)dδ=a1arsinh(b1ξ)z1,hi
(37)
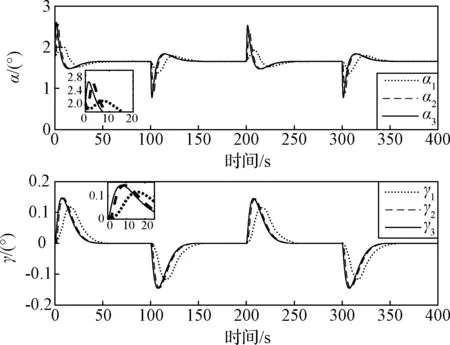
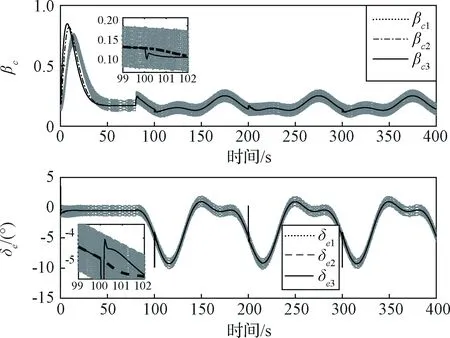
式中:0<ξ ∫z1,hi0a1arsinh(b1δ)dδ>0 (38) 同理可得 ∫z1,vj0a1arsinh(b1δ)dδ>0 (39) 故有L2>0。 对L2求导可得 [-a1arsinh(b1z1,hi)-a2arsinh(b2z2,hi)]2}+ [-a1arsinh(b1z1,vj)-a2arsinh(b2z2,vj)]}= (40) (41) 对L3求导可得 (42) (43) 综上,对L求导可得 (44) 选取参数phi≥η,pvj≥η,η为待设计正数,则式(44)可表示为 -2ηL1+Dh+Dv (45) 以HFV在33 km高空以Ma15巡航飞行为例进行仿真,其主要初始参数见表2。 表2 飞行器初始参数 考虑现实中执行机构的限制,βc限幅在[0, 1],δe限幅在[-20°, 20°]。速度参考指令为100 m/s的阶跃信号,高度参考指令为幅值为200 m的方波信号,参考指令信号均由阻尼系数为0.9,自然频率为0.15 rad/s的二阶模型给出。在仿真的第80 s引入复合扰动 (46) 动态面控制器参数设置为phi=1(i=1,2,3,4),pvj=1(j=1,2,3);IHSTD的参数设置如第2.1节所述;LESO中取ωo=30,其状态变量的初始值设为0。 为了验证所提出方法的有效性,在同样的仿真条件下,采用3种不同的控制器结构进行数字仿真。下标“1”表示滑模控制器+LESO,下标“2”表示传统反演控制器+LESO,下标“3”表示本文所设计的含LESO的动态面控制器。仿真结果如图2~6所示。 图2 高度和速度跟踪曲线Fig.2 Altitude and velocity command tracking curves 图3 高度和速度跟踪误差Fig.3 Altitude and velocity command tracking errors 图4 攻角和航迹角响应曲线Fig.4 Responses of flight-path angle and angle of attack 图2和图3分别表示了HFV的高度和速度指令跟踪曲线和跟踪误差曲线。从图2可以看出,本文提出的基于传统反演设计的动态面控制器,性能与传统的反演控制器十分接近,高度和速度都能很快地跟踪上指令信号,响应速度明显优于滑模控制器。由图3可知,本文控制器的指令跟踪误差最小,且收敛最快。图4反映了攻角和航迹角的响应曲线,可以看出攻角和航迹角均能快速收敛到新的平衡状态(攻角1.6558°,航迹角0°)。 从图2~4还可以看出,在80 s处引入复合扰动后,并没有对飞行器状态产生影响,这表明了在LESO对总和扰动的精确估计补偿作用下,3种控制器均对模型不确定项和复合扰动具有较强的鲁棒性。 图5 总和扰动估计Fig.5 Estimation of lumped disturbances 图6 控制输入Fig.6 Control inputs 图5为总和扰动估计曲线,从图5可以看出,在未引入复合扰动之前,所设计LESO能够对模型不确定项进行有效估计,引入复合扰动后,LESO能够对模型不确定项和复合扰动组成的“总和扰动”进行有效估计,实现在控制器中的动态补偿。 图6为控制输入曲线,由图6可知,高度和速度稳定跟踪上指令信号后,控制量也稳定在新的平衡状态,引入等效扰动后,控制量也随之波动,这样的振荡是为了使HFV能够抑制扰动作用的影响,保持稳定的飞行状态,但滑模控制器的控制量全程伴随着明显的高频抖振,这在工程实际中会造成极大影响,而传统的反演控制器和本文控制器则不存在这个问题。本文控制器和传统的反演控制方法的控制量曲线类似,但每当产生新的高度阶跃信号时,本文控制器的升降舵偏角会产生一个瞬时较大的值,这是由IHSTD求取虚拟控制量的微分信号造成的,适当地减小IHSTD中参数R的值可以减弱这种影响,这需要在求取虚拟控制量的微分信号的精度和减弱这种影响之间取折衷。 针对HFV巡航飞行时存在模型不确定项、未建模动态和外部扰动等的问题,设计了一种基于线性扩张状态观测器的动态面控制器。基于传统反演设计方法,引入基于反双曲正弦函数的跟踪微分器来求取虚拟控制量的微分,避免传统反演法中存在的“微分爆炸”的问题的同时,比常用的一阶低通滤波器具有更好的噪声抑制能力,大幅降低了控制器设计的复杂程度;设计了LESO,实现了对模型不确定项及复合扰动的有效估计,进而在控制器中动态补偿。 仿真结果表明,所设计的LESO能够实现对总和扰动的有效估计,大幅提升了控制器的扰动抑制能力和系统的鲁棒性;和传统滑模控制相比,所设计控制器具有更好的高度和速度指令跟踪性能。 [1] 方洋旺, 柴栋, 毛东辉, 等. 吸气式高超声速飞行器制导与控制研究现状及发展趋势[J]. 航空学报, 2014, 35(7): 1776-1786. [Fang Yang-wang, Chai Dong, Mao Dong-hui, et al. Status and development trend of the guidance and control for air-breathing hypersonic vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 1776-1786.] [2] 孙长银, 穆朝絮, 余瑶. 近空间高超声速飞行器控制的几个科学问题研究[J]. 自动化学报, 2013, 39(11): 1901-1913. [Sun Chang-yin, Mu Chao-xu, Yu Yao. Some control problems for near space hypersonic vehicles[J]. Acta Automation Sinica, 2013, 39(11): 1901-1913.] [3] Cai G B, He H F, Han X J, et al. Gain-scheduled H2tracking control of flexible air-breathing hypersonic vehicles with an LPV model[C]. The 34th Chinese Control Conference, Hangzhou, China, July 28-30, 2015. [4] Lan X J, Wang Y J, Liu L. Dynamic decoupling tracking control for the polytopic LPV model of hypersonic vehicle[J]. Science China Information Sciences, 2015, 58(9): 1-14. [5] 李昭莹, 余令艺, 刘昊,等. 高超声速飞行器非线性鲁棒控制律设计[J]. 控制理论与应用, 2016, 33(1): 1-8. [Li Zhao-ying, Yu Ling-yi, Liu Hao, et al. Nonlinear robust controller design for hypersonic vehicles[J]. Control Theory & Applications, 2016, 33(1): 1-8.] [6] 董朝阳, 路遥, 王青. 高超声速飞行器指令滤波反演控制[J]. 宇航学报, 2016, 37(8): 957-963. [Dong Chao-yang, Lu Yao, Wang Qing. Command filtered backstepping control for hypersonic vehicle[J]. Journal of Astronautics, 2016, 37(8): 957-963.] [7] Wu G H, Meng X Y. Nonlinear disturbance observer based robust backstepping control for a flexible air-breathing hypersonic vehicle[J]. Aerospace Science and Technology, 2016, 54: 174-182. [8] An H, Liu J X, Wang C H, et al. Approximate back-stepping fault-tolerant control of the flexible air-breathing hypersonic vehicle[J]. IEEE-ASME Transactions on Mechatronics, 2016, 21(3): 1680-1691. [9] 陈洁, 周绍磊, 宋召青. 基于不确定性的高超声速飞行器动态面自适应反演控制系统设计[J]. 宇航学报, 2010, 31(11): 2550-2556. [Chen Jie, Zhou Shao-lei, Song Zhao-qing. Hypersonic aircraft dynamic surface adaptive backstepping control system design based on uncertainty[J]. Journal of Astronautics, 2010, 31(11): 2550-2556.] [10] Bu X W, Wu X Y, Zhang R Z, et al. A neural approximation-based novel back-stepping control scheme for air-breathing hypersonic vehicles with uncertain parameters[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2016, 230(3): 231-243. [11] 韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008. [12] 刘晓东, 黄万伟, 禹春梅. 含扩张状态观测器的高超声速飞行器动态面姿态控制[J]. 宇航学报, 2015, 36(8): 916-922. [Liu Xiao-dong, Huang Wan-wei, Yu Chun-mei. Dynamic surface attitude control for hypersonic vehicle containing extended state observer[J]. Journal of Astronautics, 2015, 36(8): 916-922.] [13] 杨文骏, 张科, 张明环, 等. 基于ESO的高超声速飞行器非线性动态逆控制[J]. 西北工业大学学报, 2016, 34(5): 805-811. [Yang Wen-jun, Zhang Ke, Zhang Ming-huan, et al. ESO based nonlinear dynamic inversion control for hypersonic flight vehicle[J]. Journal of Northwestern Polytechnical University, 2016, 34(5): 805-811.] [14] Guo B Z, Zhao Z L. On convergence of the nonlinear active disturbance rejection control for MIMO systems[J]. SIAM Jounal on Control and Optimization, 2013, 51(2): 1727-1757. [15] Guo B Z, Zhao Z L. On the convergence of an extended state observer for nonlinear systems with uncertainty[J]. Systems & Control Letters, 2011, 60(6): 420-430. [16] Jiang T T, Huang C D, Guo L. Control of uncertain nonlinear systems based on observers and estimators[J]. Automatica, 2015, 59: 35-47. [17] Ran M P, Wang Q, Dong C Y. Stabilization of a class of nonlinear systems with actuator saturation via active disturbance rejection control[J]. Automatica, 2016, 63: 302-310. [18] 周涛. 基于反双曲正弦函数的跟踪微分器[J]. 控制与决策, 2014, 29(6): 1139-1142. [Zhou Tao. Tracking differentiator based on inverse hyperbolic sine function[J]. Control and Decision, 2014, 29(6): 1139-1142.] [19] Gao Z Q. Active disturbance rejection control: a paradigm shift in feedback control system design[C]. The 2006 American Control Conference, Minneapolis, USA, June 14-16, 2006. [20] Xu H J, Mirmirani M D, Ioannou P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 829-838. [21] 邵星灵, 王宏伦. 线性扩张状态观测器及其高阶形式的性能分析[J]. 控制与决策, 2015, 30(5): 815-822. [Shao Xing-ling, Wang Hong-lun. Performance analysis on linear extended state observer and its extension case with higher extended order[J]. Control and Decision, 2015, 30(5): 815-822.] 通信地址:陕西省西安市友谊西路127号西北工业大学航天学院250信箱张科学科组(710072) 电话:13572137983 E-mail: 13572137983@163.com LESO-Based Dynamic Surface Control for a Hypersonic Flight Vehicle YANG Wen-jun1,2, ZHANG Ke1,2, WANG Pei1,2 (1. National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China;2. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China) A linear estended state observer (LESO)-based dynamic surface controller is proposed in this paper for the cruising control problem of a hypersonic flight vehicle (HFV) with model parametric uncertainties and external disturbances. First of all, the longitudinal model of the HFV is denoted, and the decoupling of the altitude and velocity is realized via the nonlinear dynamic inversion (NDI) technique. Then, combining with the conventional back-stepping technique, a tracking differentiator based on the inverse hyperbolic sine function (IHSTD) is adopted to attain the derivatives of the virtual control laws, which avoids the problem of “differentiation explosion”. And then a LESO is designed for the precise estimation and compensation of the “lumped disturbance” containing parametric uncertainties and external disturbances, which tremendously improves the ability of the disturbance rejection of the system. Finally, the stability of the proposed approach is analyzed by means of the Lyapunov stability theory. The exploited approach guarantees the asymptotic stability and robustness of the system, and the simulation results demonstrate the validity of the proposed method. Hypersonic flight vehicle (HFV); Tracking differentiator; Linear extended state observer (LESO); Disturbance rejection; Dynamic surface control; Robustness 2017- 04-21; 2017- 05-23 国家自然科学基金(61174204,61101191,61502391) TJ765.2; V448.2 A 1000-1328(2017)08-0830-09 10.3873/j.issn.1000-1328.2017.08.007 杨文骏(1987-),男,博士生,主要从事飞行器导航、制导与控制等方面的研究。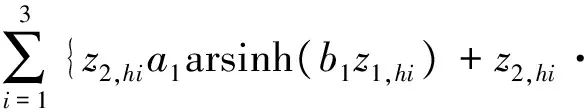
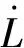
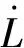
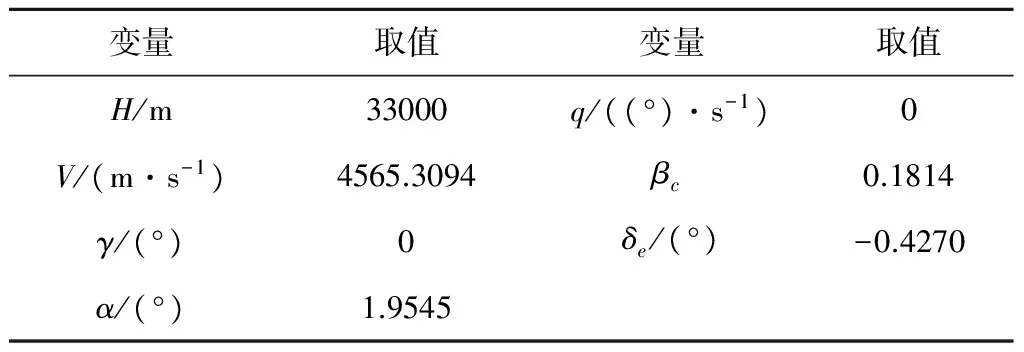
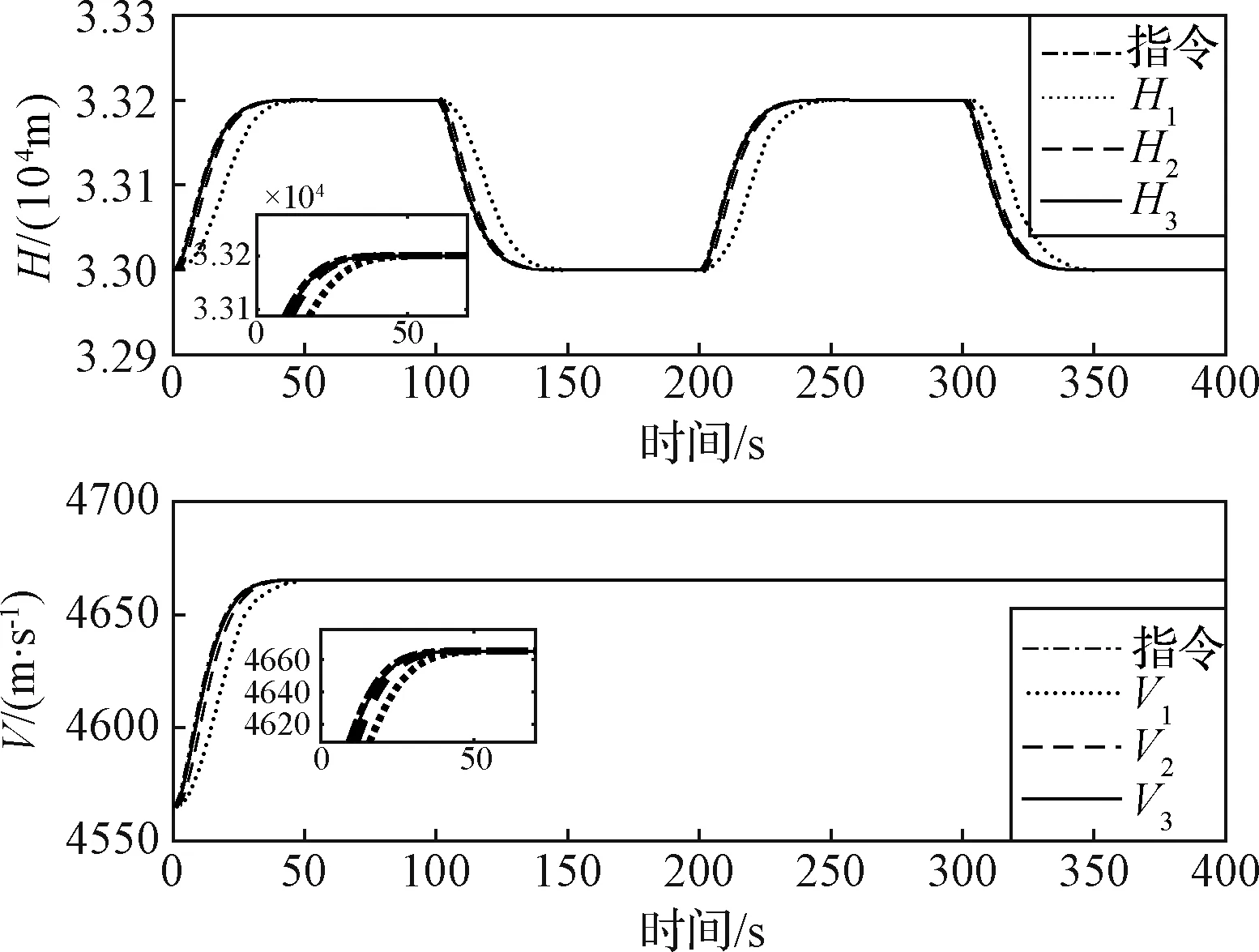
3 仿真校验


4 结 论
