面向微小卫星绕飞任务的平滑估计器与多脉冲制导算法

郭久玖，孟子阳

(1. 北京跟踪与通信技术研究所，北京 100094；2. 清华大学精密仪器系，北京 100084)

面向微小卫星绕飞任务的平滑估计器与多脉冲制导算法

郭久玖1,2，孟子阳2

(1. 北京跟踪与通信技术研究所，北京 100094；2. 清华大学精密仪器系，北京 100084)

首先针对传统主动绕飞算法中存在的相角跳变问题，提出一种新型的平滑估计器，解决了经典扩展卡尔曼滤波(EKF)算法应用于主动绕飞过程中存在的估计值抖动和反转问题。接下来，针对传统多脉冲算法不考虑轨道精度和燃料消耗的问题，提出一种改进的导航点规划的最省燃料多脉冲主动绕飞算法。该算法将燃料最省的路径规划问题转化为导航点及相关参数的规划问题，并结合二次规划计算得出满足给定绕飞精度的绕飞路径。最后，将所提出的算法应用于20 kg级的微小卫星空间交互任务当中。仿真结果表明，对于经典的圆形轨迹绕飞应用，本文所给出的算法能够避免相角跳变现象的出现。同时，相比于传统的多脉冲算法最多可以降低42.2%的燃料消耗。

主动绕飞；相角补偿；燃料最省；导航点

0 引 言

空间轨道是一种有限的资源，虽然目前还没有到达稀缺的地步，随着时间的推移，人类的航天活动越来越频繁，越来越多的空间航天器老化失控导致空间垃圾增多、空间环境恶化，人们必须更加安全、有效地利用空间资源。为了保护空间轨道资源，不仅需要国际社会的密切合作，还需大力发展在轨服务技术[1]。在轨服务技术主要包含在轨目标监测、在轨辅助变轨、在轨燃料补给、在轨故障修复等几方面的内容。近年来，随着微小卫星技术的发展，基于微小卫星的在轨服务技术有了长足的发展，并对空间碎片的探测和保护有限的空间轨道资源发挥着重要作用，如美国的轨道快车[1-3]计划和MiTEx微小卫星计划[1-4]等。

对于微小卫星的在轨目标监测来说，空间交会过程中的主动绕飞过程是其核心问题。通常空间交会过程中追踪航天器轨道和目标航天器轨道处于同一平面内，分为V方向接近和R方向接近两种方式。但自主在轨服务的航天器，为了全方位地监测目标航天器，需要设计各种任意轨道，实现主动绕飞。

Hablani等[5]以C-W方程的解析解为基础，结合斜滑道算法[6]，提出了一种多脉冲斜滑道算法，以实现追踪航天器的接近，分离及主动绕飞。这一算法在初末条件确定后，以固定时间转移，对于脉冲施加的间隔和次数与精度之间的关系没有明确说明；对于速度与距离的假设没有考虑燃料的节省问题[7-8]，因而实际消耗了过多燃料。国外一些研究在文献[5]的基础上考虑了视场[9-10]、姿态[9-10]、及系统鲁棒性[9-11]的影响，但缺少节省燃料的考虑。Sultan等[16-18]在编队飞行重构轨迹生成中引入导航点将燃料最优轨迹问题转化为导航点相关参数的优化问题。

国内王峰等[12]在文献[5]的基础上，考虑有摄动情况下的任意平面主动绕飞的实现。通过对绕飞轨迹偏差进行分析，给出达到预定轨道制导精度的最小脉冲绕飞。王峰等[13]考虑安全速度、制导误差及最大加速度等约束的条件后，对于多脉冲斜滑道算法进行了改进，确定了脉冲施加的最小次数和时间间隔，不足的是没有节省燃料的考虑。梁立波等[14]提出了一种斜滑道制导算法，采用对数函数映射法进行脉冲寻优，实现燃料的最省交会。但是该方法对于主动绕飞过程并不完全适用。朱彦伟等[19]在Sultan的基础上提出一种基于导航点的近圆轨道航天器相对运动的固定时间状态转移轨迹生成策略，但是这一方法对于主动绕飞过程缺少必要约束。

使用方位角的相对导航方面，传统的多脉冲算法[5-6]使用简单的反三角函数来表示目标航天器的方位角。三角函数周期性使得方位角的相角在绕飞超过180度的情况下必然发生相角跳变。接近过程[8,13-14]整个过程中方位角的变化通常小于180度，可以通过初相的设定来避免方位角相角的跳变。于主动绕飞过程，文献[12] 采用简单地周期性延拓来解决相角跳变，但对于绕飞周期动态变化和椭圆绕飞该方法不适用。

本文在传统多脉冲算法的基础上，通过设计相角跳变补偿的平滑估计器设计以保证估计值稳定有效，并考虑绕飞的轨道精度和最低燃料消耗，结合二次规划模型，提出一种燃料最省的多脉冲主动绕飞算法，解决了给定绕飞精度下主动绕飞的路径规划问题。

1 相角跳变补偿的相对导航算法

1.1 二体交会问题的动力学建模

在近圆轨道且两航天器相距很近的情况下，追踪航天器相对于目标航天器的运动可用Clohessy-Wiltshire(C-W)方程表示

(1)

式中:ω为轨道角速度，ax、ay、az分别是X轴、Y轴、Z轴的加速度，N(0,σ)代表均值为0，标准差为σ的正态分布，在不考虑摄动的情况下ax=ay=az=0。

设追踪航天器的位置和速度分别为

(2)

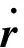
(3)

式中:Φ均为3×3的矩阵，具体值为：

1.2 相角跳变补偿的平滑估计器设计过程模型

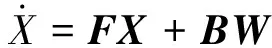
(4)

式中:F是系统过程矩阵

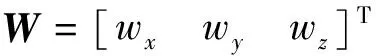
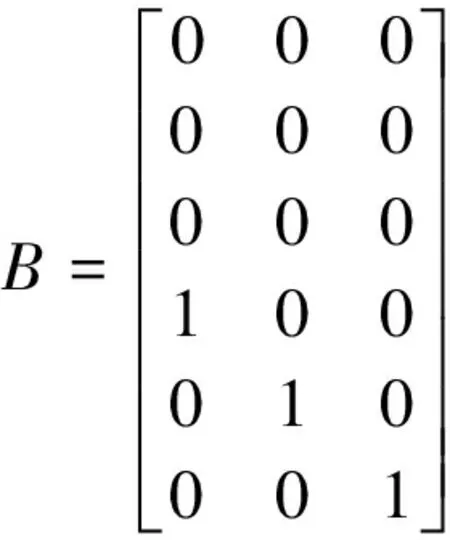
C-W方程是一个连续时间的线性方程，按采样周期Ts进行离散化后，由k-1时刻对k时刻的状态预测为

(5)

量测模型：假设目标航天器和追踪航天器运行在两个相近的轨道上，向量rCT为追踪航天器指向目标航天器的位置矢量。在追踪航天器的本地垂直坐标中，rCT可以被表示为

(6)

基于测量系统中获得的原始测量数据，即相对距离r、方位角θy1、俯仰角θz1，rCT可以表示为

rCT=r[cosθy1cosθz1sinθz1-sinθy1cosθz1]T

(7)

设vy和vz是角度测量的噪声，vr是测距噪声，所有噪声均为互相独立的白噪声。在目标航天器的本地垂直坐标系中，x=-rCTx，y=-rCTy，z=-rCTz，则测量方程可以写为

(8)

将测量方程重新写成标准的卡尔曼滤波向量形式，γ=h(x)+v，则量测方程h(x)为

(9)

上述理论对于主动绕飞过程，测量系统输出的方位角实际变化范围为[0,2π)，但系统方程θy1=arctan(-z/x)的值域却是(-π/2,+π/2)，直接将上述量测方程用于扩展卡尔曼滤波算法必然导致在nπ/2(n=1,2,3,…)的估计值突变，发生π相变从而使得扩展卡尔曼滤波估计经历瞬时的估计错误，最终导致估计值的抖动与反转现象，如图1～2所示。

为消除扩展卡尔曼滤波算法估计值的抖动与反转，重新对方位角θy1进行定义

θy1=arctan(y,x)

(10)

(11)

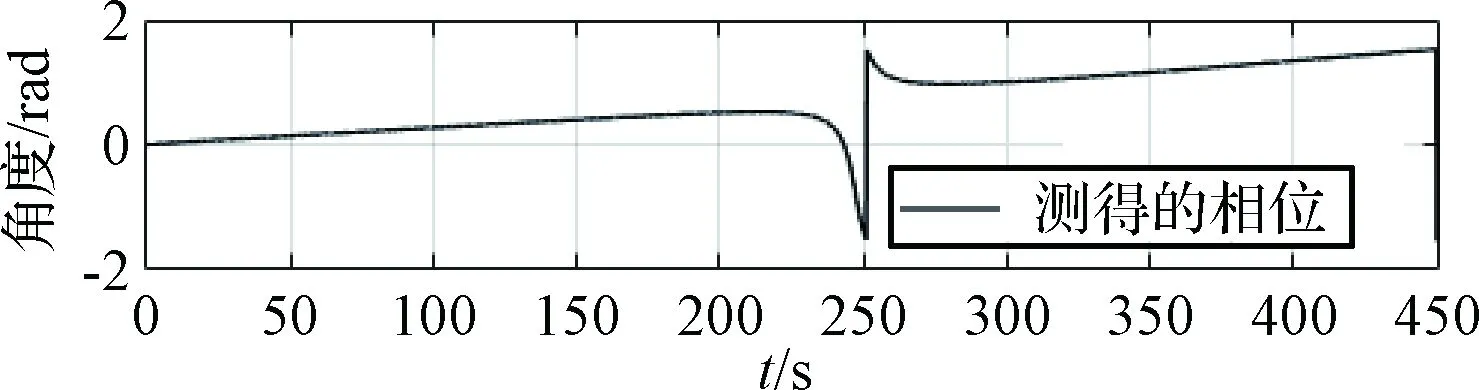
图1 经典EKF算法中相角的π相变Fig.1 π phase-burst in classical EKF algorithm

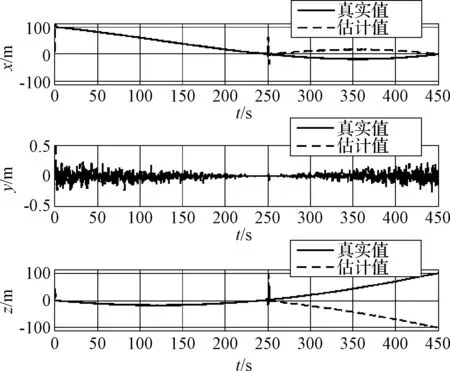
图2 经典EKF算法中π相变引起的状态抖动和反转Fig.2 π phase-burst induced by chattering and reversion in classical EKF Algorithm

此时仍然存在2π相变，通过补偿相角的方式来达到估计器的平滑估计。测量的方位角经过π(-π)时检测是否有角度跳变产生，通过测量的角度跳变的方向(由+π到-π或是由-π到+π)，在测量的角度量中减去(或者加上)跳变的2π相位，从而达到相角补偿的目的，消除2π相变引起的抖动。

2 燃料最省的主动绕飞算法

多脉冲过程[5]中最重要的是确定每个脉冲的施加位置、大小和方向。导航点规划算法[15-19]通过引入导航点的概念，将轨迹优化的问题转化为导航点及相关的参数选择的问题。

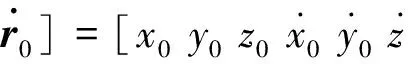
为了表示每个导航点的在理想转移轨迹r上的位置，需建立轨迹r与伪时间Δtui(i=1,2,…,N-1)的任意对应关系；通常为了计算方便设定为线性关系，则第k个导航点的位置表达如下

(12)

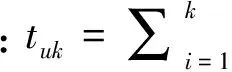
脉冲施加的时间需要建立另一组时间变量Δti(i=1,2,…,N-1)，用于表示第i个和第i+1个导航点之间的时间间隔。每次脉冲的速度增量Δvi可得

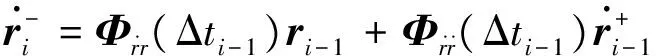
i=2,…,N

(13)

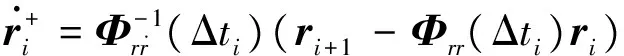
i=1,2,…,N-1

(14)

(15)

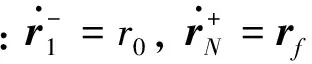
对于整个转移过程求取Δvsum为优化指标

(16)

速度变化量Δv=Δvsum和航天器排出的推进剂的质量mp关系如下

(17)

式中:mp为消耗的推进剂质量，mo为航天器推进前的初始质量,Isp是比冲，为一常数。因此整个绕飞过程燃料的消耗质量为

(18)

mp和Δvi都是相邻脉冲间隔时间Δti和相邻导航点间的伪间隔时间Δtui的函数，可以通过对Δti和Δtui的选择来达到对mp和Δvi的优化。因此，决策变量D定义为

D=[Δt1…ΔtN-1 Δtu1 … ΔtuN-1]

(19)

容易知道，决策变量D共包括2N-2个决策变量。

整个优化模型如下：

(20)

式中:Δt=tf-t0。

决策变量的初值可取为

D=[ Δt/(N-1)…Δt/(N-1)

Δt/(N-1)…Δt/(N-1)]

即导航点位置等间隔分布，脉冲间隔时间相等。目标函数min{mp}=min{F(D)}可以采用二次规划算法进行数值求解。

上述算法仍存在几点不足可改进。一是没有绕飞精度的限制；实际转移轨迹r′与理想转移轨迹r的偏差没有具体的评价指标。二是必须在固定脉冲数N的情况下方可使用优化模型，无法得出关于脉冲数的最优解。三是决策变量的边界条件设置不完全合理，实际过程中两相邻脉冲之间应存在最小间隔时间Tivl>0，转移时间Δt=tf-t0内的理论最大脉冲数为

(21)

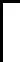
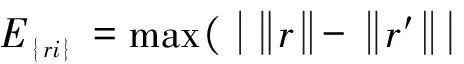
改进后的算法流程如图3所示。

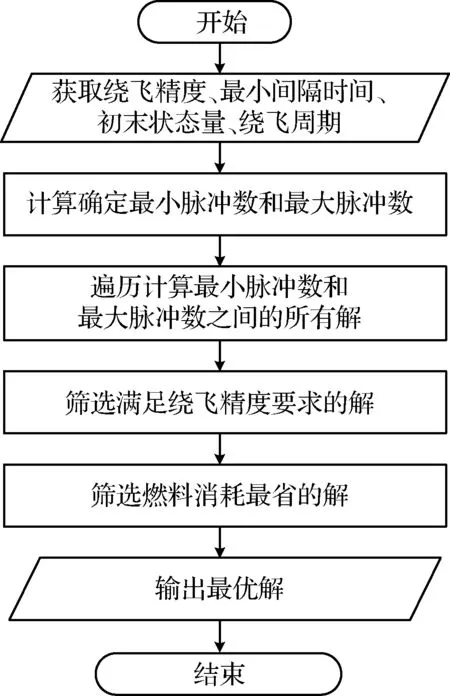
图3 改进型燃料最省导航点规划算法流程图Fig.3 Flow chart for improved most fuel-saving way-point based planning algorithm

3 仿真校验与结果分析

仿真平台：使用同一台计算机进行实验，主机CPU为Intel(R)Core(TM)i5-4200U@2.6GHz，内存为4GB@1600MHz(DDR3)。Windows 10(64位)操作系统，使用Matlab R2015a Simulink组件进行仿真。基于上述平台，针对每一给定脉冲数的单次仿真计算时间约为20秒，整个遍历计算过程通常约耗时数分钟到数十分钟。

仿真任务设计：面向20 kg级的微小卫星，对所提出的空间自主交会算法进行仿真校验。绕飞圆形轨迹位于XZ平面，半径R=100 m，起始点为(100,0,0)，并沿顺时针方向绕飞，最后回到起始点。

采用清华大学智能微系统实验室2004年研制的NS1试验卫星和2015年研制的MEMS试验卫星为仿真对象。系统参数为：轨道高度536 km；轨道偏心率0(或不大于0.001)轨道周期100.5 min；重量23.3 kg；推进系统为液氨推进系统，额定比冲为900 Ns/kg；微反射镜系统测距范围1～500 m，精度0.5 m；两轴角度精度0.1°；测量输出频率优于0.1 s。

3.1 相角跳变补偿的相对导航算法仿真

转移时间T=100.5 min=6030 s，脉冲数N=4，脉冲间隔时间为1507.5 s，脉冲施加的位置分别为(100,0,0)、(0,0,-100)、(-100,0,0)和(0,0,100)。扩展卡尔曼滤波算法的采样周期Ts=0.25 s。设定的初始估计误差为

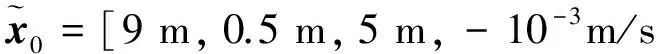
-10-4m/s,-3×10-4m/s]

图4是仿真过程中三个坐标的估计值(虚线)与真实值(实线)对比图，从上到下分别是X,Y,Z轴方向的相对位置分量。由于X和Z方向坐标动态范围大，使得估计精度难以辨别，下面用估计值减去真实值作残差图。

图5是整个仿真过程三个坐标的估计残差，从上到下分别是X,Y,Z轴。可以看出，各个方向上的残差都是在0.2 m到0.4 m之间，说明三轴坐标的估计值与真实值的一致性非常高。通过对估计值与真实值经常采样点分析处理，可以得出三轴相对位置精度如表1所示。

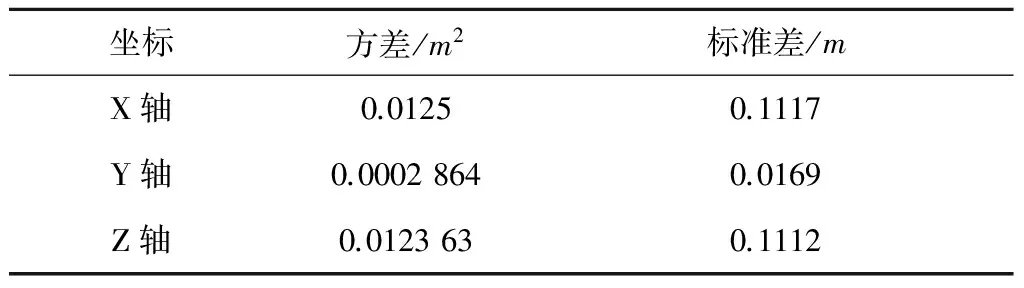
表1 三轴相对位置精度

通过对三轴位置精度(即XYZ方向的标准差)求取平方根可以得出合成的标准差为0.1585 m，从而可以得出估计精度为0.4756 m(3σ标准)。

3.2 燃料最省的绕飞导航点规划算法仿真

设置转移时间为T=100.5 min=6030 s，但对脉冲数不限定，要求绕飞精度优于2 m，相邻脉冲之间的最小间隔时间Tivl=200 s，最大脉冲数Nmax=30。建立理想转移轨迹r与伪时间Δtui的线性关系

(22)

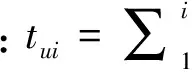
根据每一个脉冲数的数值仿真的结果(见表2),由于决策变量D的向量长度过长，不便于表示，

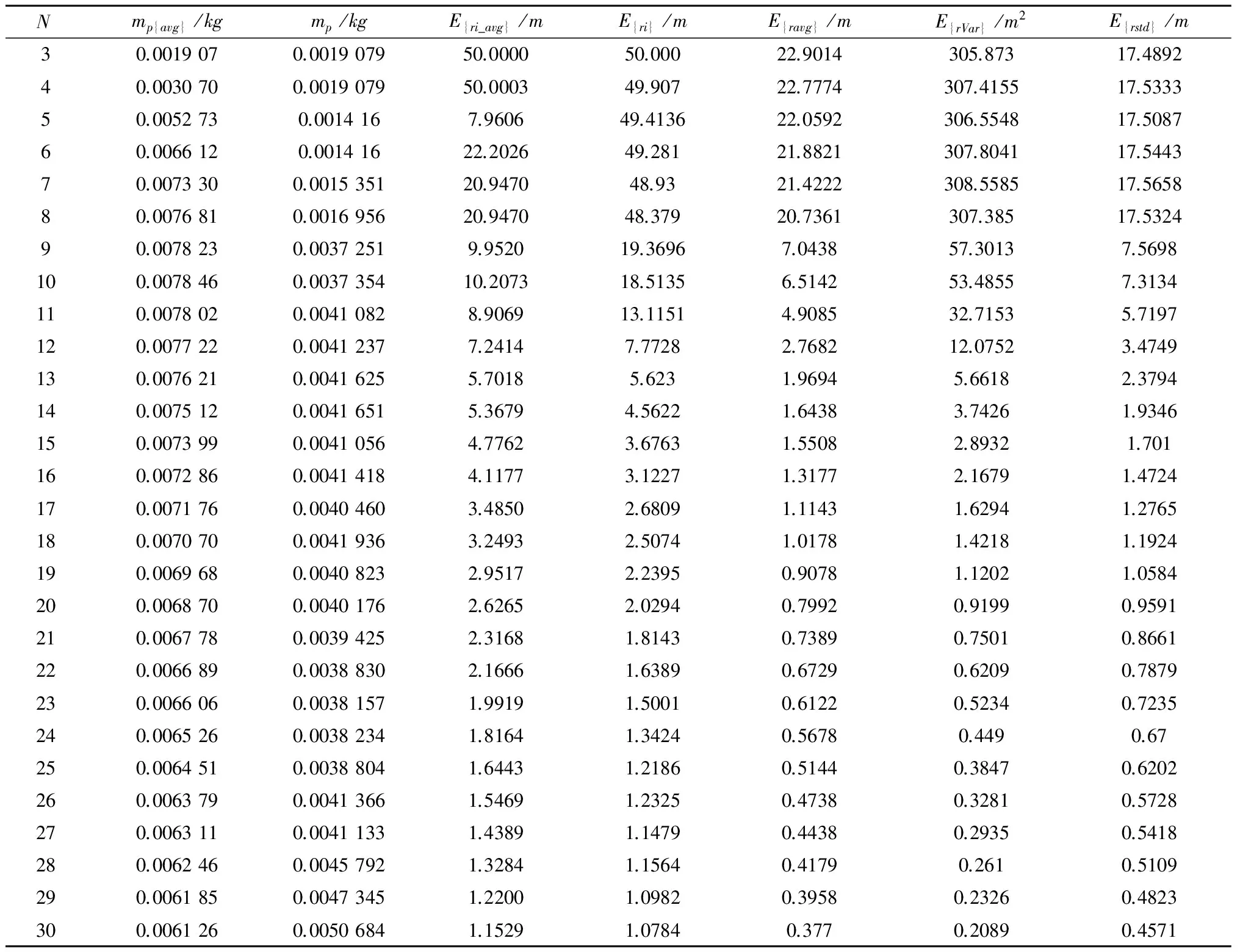
表2 脉冲数与燃料消耗及绕飞精度关系

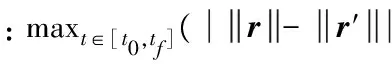
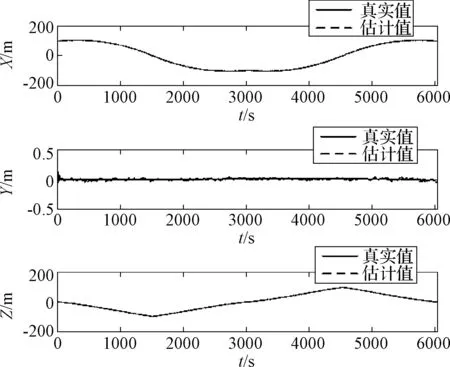
图4 三轴估计值与真值对比图Fig.4 Comparison between three-axis estimation and true values

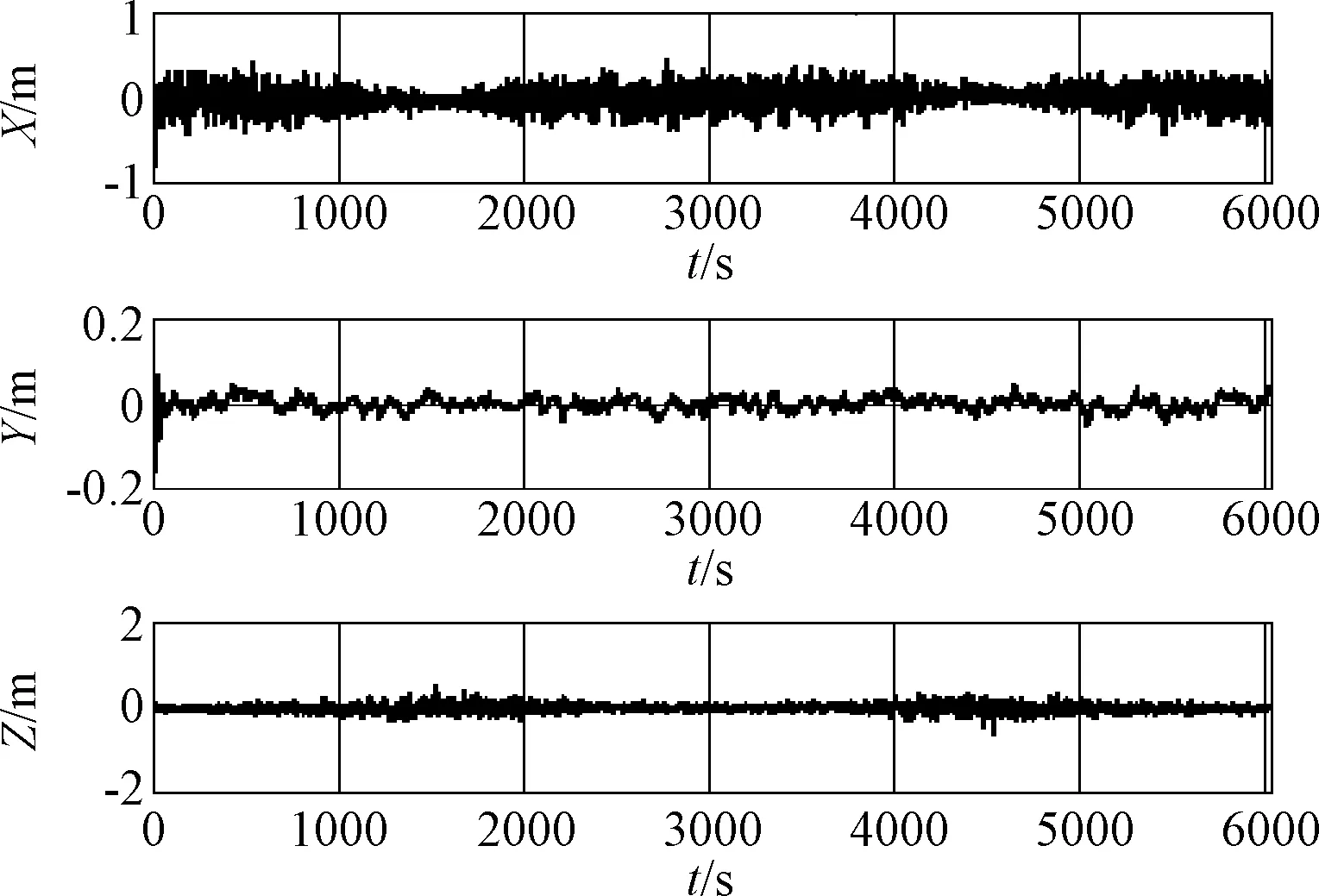
图5 三轴估计值残差Fig.5 Three-axis estimation residual errors

故表中略去。分析表2可知，最优解为N=23时的解(决策变量D)，实际轨线如图6所示，燃耗为0.0038157 kg，相对于传统的平均分脉冲间隔时间方法的燃耗(0.006606 kg)可以降低42.2%的燃料消耗，绕飞精度为1.5001 m，高于预期的2 m。

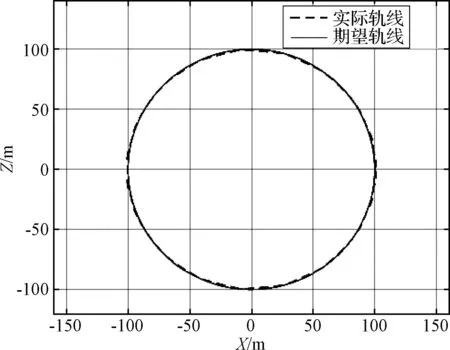
图6 最优解的理想转移轨迹和实际转移轨迹对比Fig.6 Comparison between desired trajectory and real trajectory of optimal solution

最优解为N=23，

D= [467.164 353.3131 290.4598 237.5537 203.8572 202.3188 200.1103 212.9569 248.1543 286.2462 313.8533 313.8533 286.2462 248.1542 212.9565 200.2451 200.1473 203.9197 237.5533 290.4598 353.3131 467.1640 143.2169 204.9192 266.4085 308.0448 323.0533 342.1695 330.7470 319.0044 296.4416 257.7384 223.2566 223.2566 257.7384 296.4417 319.0048 330.7041 342.2575 323.0098 308.0446 266.4078 204.9186 143.2162]

根据N=23时最优解的决策向量D,可以解出整个绕飞过程每个脉冲的编号与其相对位置坐标(XYZ)及与下一脉冲的间隔时间,如表3所示。

4 结 论

本文针对微小卫星的多脉冲主动绕飞算法进行研究，改进了经典的多脉冲斜滑交会算法并进行实例仿真校验。

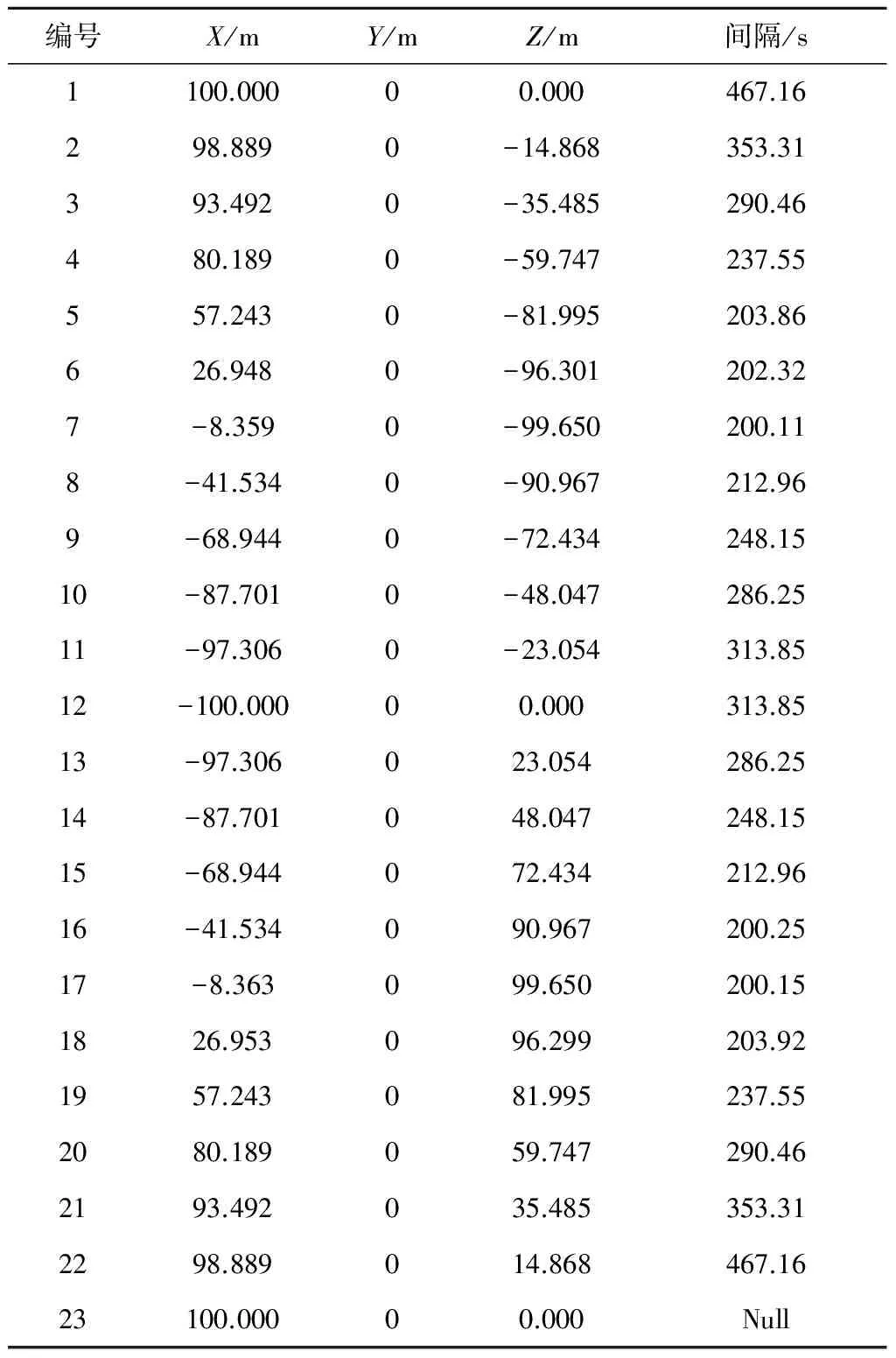
表3 最优解脉冲施加位置和间隔时间(N=23)

1)通过设计补偿相角跳变的平滑估计器消除了相角跳变对估计值的不良影响，解决了传统的扩展卡尔曼滤波算法应用于主动绕飞过程中的估计值抖动和反转问题。

2)提出了最省燃料的多脉冲主动绕飞算法并进行数值仿真，最多可以降低42.2%的燃料消耗，减少了使用传统的平均分脉冲间隔时间算法导致的燃料浪费。

3)定义理想轨线与实际轨线的误差为绕飞精度，并在给定精度下，通过对导航点的规划，设计了最省燃料的多脉冲主动绕飞算法。

[1] 陈士明, 周志成, 曲广吉,等. 国外地球静止轨道在轨服务卫星系统技术发展概况[J]. 国际太空, 2014, 2014(4): 55-63. [Chen Shi-ming, Zhou Zhi-cheng, Qu Guang-ji, et al. Survey of foreign GEO on-orbit servicing system development [J]. Space International, 2014, 2014(4): 55-63]

[2] 梁斌, 徐文福, 李成, 等. 地球静止轨道在轨服务技术研究现状与发展趋势[J]. 宇航学报, 2010, 31(1): 1-13. [Liang Bin, Xu Wen-fu, Li Cheng, et al. Current status and develop trend of the study on on-orbit servicing technology [J]. Journal of Astronautics, 2010, 31(1): 1-13.]

[3] 崔乃刚, 王平, 郭继峰,等. 空间在轨服务技术发展综述[J]. 宇航学报, 2007, 28(4): 805-811. [Cui Nai-gang, Wang Ping, Guo Ji-feng, et al. Review of development in on-orbit servicing technology [J]. Journal of Astronautics, 2007, 28(4): 805-811.]

[4] 梁斌, 杜晓东, 李成, 等. 空间机器人非合作航天器在轨服务研究进展[J]. 机器人, 2012, 34(2): 242-256. [Liang Bin, Du Xiao-dong,Li Cheng, et al. Advance in space robot on-orbit servicing for non-cooperative spacecraft [J]. Robot, 2012, 34(2): 242-256.]

[5] Hablani H B, Tapper M, Dana-Bashian D. Guidance algorithms for autonomous rendezvous of spacecraft with a target vehicle in circular orbit[C]. AIAA Guidance, Navigation, and control conference and Exhibit, Montreal, Canada, August 6-9, 2001.

[6] Pearson D J. The glideslope approach[C]. AAS/NASA Intl. Symposium on Orbital Mechanics and Mission Design, Greenbelt, MD, USA, Apr. 24-27, 1989.

[7] Jie J, Yu Y, Kemao M. Continuous optimal terminal proximity guidance algorithm for autonomous rendezvous and docking[J]. Information Technology Journal, 2013, 12(5): 1011-1017.

[8] Wu S, Sun Z, Radice G, et al. Guidance algorithms for proximity to target spacecraft[J]. Aircraft Engineering & Aerospace Technology, 2013, 83(83): 146-153.

[9] Nolet S. Development of a guidance, navigation and control architecture and validation process enabling autonomous docking to a tumbling satellite[D]. Cambridge: Massachusetts Institute of Technology, 2007.

[10] Fejzic A. Development of control and autonomy algorithms for docking to complex tumbling satellites[D].Cambridge:Massachusetts Institute of Technology, 2008.

[11] Sheng D, Yang X, Karimi H R. Robust control for autonomous spacecraft evacuation with model uncertainty and upper bound of performance with constraints[J]. Mathematical Problems in Engineering, 2014, 2014(4): 1-16.

[12] 王峰, 陈雪芹, 曹喜滨,等. 在轨服务航天器任意轨道主动绕飞[J]. 哈尔滨工业大学学报, 2014, 46(5): 6-10. [Wang Feng, Chen Xue-qin, Cao Xi-bin, et al. The initiative flyaround of on-orbit-servicing spacecraft in-any-plane [J]. Journal of Harbin Institute of Technology, 2014, 46(5): 6-10.]

[13] 王峰, 曹喜滨. 受约束在轨服务航天器近距离交会制导算法[J]. 系统工程与电子技术, 2006, 28(10): 1578-1582. [Wang Feng, Cao Xi-bin. Guidance algorithms for near distance rendezvous of on-orbit-servicing spacecraft under constraints [J]. Systems Engineering and Electronics, 2006, 28(10): 1578-1582.]

[14] 梁立波，罗亚中，唐国金．航天器近距离交会斜滑制导算法[J]．国防科技大学学报，2009，31(5)：125-129. [Liang Li-bo, Luo Ya-zhong, Tang Guo-jin. Glideslope guidance algorithm for close range rendezvous of spacecraft [J]. Journal of National University of Defense Technology, 2009, 31(5): 125-129.]

[15] 杨乐平. 航天器相对运动轨迹规划与控制[M]. 北京：国防工业出版社, 2010.

[16] Sultan C, Seereeram S, Mehra R. Matrix Inequalities and energy optimal reconfiguration for formation flying spacecraft[C].AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, Rhode Island, Aug. 16-19, 2004.

[17] Sultan C, Seereeram S, Mehra R K. Minimization and equalization of energy for formation flying reconfiguration[C]. IEEE International Conference on Robotics and Automation, New Orleans , LA , Apr. 26-May 5, 2004 .

[18] Sultan C, Seereeram S, Mehra R K. Energy optimal multi-spacecraft relative reconfiguration of deep space formation flying[C]. The 43rd IEEE Conference on Decision and Control, Atlantis, Paradise Island, Bahamas, Dec. 14-17, 2004.

[19] 朱彦伟, 杨乐平, 任仙海. 一种基于导航点的航天器相对运动轨迹生成策略[J]. 国防科技大学学报, 2008, 30(3):1-4.[Zhu Yan-wei, Yang Le-ping, Ren Xian-hai. Trajectory generation strategy based on way-points for spacecraft relative motion[J]. Journal of National University of Defense Technology, 2008, 30(3):1-4.]

通信地址：北京市海淀区北清路26号院(100094)

电话：(010)66368126

E-mail:guojj2012@126.com

孟子阳(1984-)，男，博士，副教授，主要从事微纳航天器系统等领域研究。本文通信作者。

通信地址：北京市海淀区清华大学9003大楼(100084)

电话：(010)62776000

E-mail: ziyangmeng@tsinghua.edu.cn

Smooth Estimator and Multi-Pulse Guidance Algorithm for MicrosatelliteAutonomous Circumnavigation Mission

GUO Jiu-jiu1,2, MENG Zi-yang2

(1. Beijing Institute of Tracking and Telecommunication Technology, Beijing 100094, China;2. Department of Precision Instrument, Tsinghua University, Beijing 100084, China)

Firstly, aiming at the phase-burst problem of the traditional autonomous circumnavigation algorithm, a new smooth estimator is proposed to compensate the estimation chattering and reversion induced by the classical extended Kalman filter (EKF) algorithm. Then, since the traditional multi-pulse guidance algorithm does not consider the orbit accuracy and fuel consumption, we propose an improved fuel-saving guidance algorithm based on navigation-point planning. The fuel-saving guidance algorithm transforms the problem of the fuel-saving path planning into the parameters of the navigation-point planning, which can be solved by using the quadratic programming given while the demand of fly-around orbit accuracy is satisfied. Finally, the proposed algorithm is applied to the space rendezvous mission of the 20kg-level small satellites. Simulation results show that the proposed algorithm is capable of avoiding the phase-burst problem induced by classical in-plane circumnavigation algorithm. Meanwhile, the fuel consumption is reduced up to 42.2% compared with the traditional multi-pulse glideslope algorithm.

Autonomous circumnavigation; Phase-burst compensation; Fuel-saving; Navigation-point

2016-10-24;

2017-06-15

国家自然科学基金(61503249)；国家重点研发计划(2016YFB0500900)

V448.21

A

1000-1328(2017)08-0822-08

10.3873/j.issn.1000-1328.2017.08.006

郭久玖(1994-)，男，硕士生，主要从事遥感技术及应用研究。