具强阻尼的随机波动方程随机吸引子的分形维数*

周盛凡, 王 蒙

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

具强阻尼的随机波动方程随机吸引子的分形维数*

周盛凡, 王 蒙

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

主要考虑带可加与可乘白噪声的具强阻尼的随机波动方程的随机吸引子的分形维数的上界估计式.首先,利用Ornstein-Uhlenbeck过程将具白噪声的随机方程转化成以随机变量为参数的无噪声的随机方程;然后,把该随机方程的2个解之差适当分解成2个部分之和,并分别估计这2个部分的模及某些随机变量的期望的有界性;最后,得到了所研方程的随机吸引子的分形维数的上界估计式.

随机波动方程;随机吸引子;强阻尼;分形维数

0 引 言

波动方程是最重要的数理方程之一,描述物体的振动和波的传播,被广泛研究.在实际生活中,许多问题的演变同时伴随着不确定因素的干扰,仅用确定性的方程去描述这些问题是不够的,必须用随机方程来描述.

本文考虑如下带可加与可乘白噪声的2个具强阻尼的随机波动方程：

(1)

utt-αΔut+ut+f(u)-Δu=g(x)+cu∘dWdt, t∈(0,+∞).

(2)

需满足的边初值条件为

(3)

对方程(1)和(2)中的f(u)作如下假设:存在常数c0,c1,c2≥0,使得

(4)

由随机波动方程解确定的随机动力系统的随机吸引子已经得到了不少学者的研究[1-11].当α=0时,方程(1)和(2)退化为无强阻尼的随机波动方程,文献[1-8]证明了这类方程的随机吸引子的存在性,并对其Hausdorff维数与分形维数的上界进行了估计.对于无噪声的强阻尼波动方程(即方程(1)或(2)中无噪声项)的整体吸引子及其维数,已有一些重要结果[9-10].对于有白噪声扰动的强阻尼的随机波动方程(即方程(1)或(2)中α≠0且有白噪声项时),至今仅有文献[11-13]分别证明了由方程(1)和(2)满足条件(3)和(4)的解确定的随机动力系统随机吸引子的存在性,而随机吸引子的分形维数的有界性仍未见报道.吸引子的分形维数的有界性是个重要的研究课题.根据文献[14],对于自然数n,如果作为度量空间的紧子集的吸引子的分形维数小于n/2,那么这个吸引子的拓扑维数最多是n,从而吸引子可由最多n个独立参数来表示,这意味着相应的动力系统的渐近行为是有限维的,但Hausdorff维数没有这个性质.本文利用文献[7-8]的方法,研究了当α≠0时,方程(1)和(2)满足条件(3)和(4)时随机吸引子的分形维数的上界估计式.

1 带可加白噪声的随机波动方程

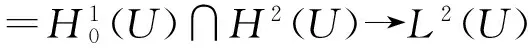
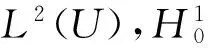
(5)

((u,v))=∫Uu·vdx, ‖u‖=((u,u))12, ∀u,v∈H10(U);

(6)

(7)

(8)

式(8)中:

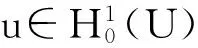
在Ω上定义一族变换θt:θtω(·)=ω(·+t)-ω(t),t∈R,ω∈Ω,则(Ω,F,P,(θt)t∈R)是遍历的度量动力系统.引入Ornstein-Uhlenbeck过程

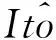
(9)

E[|z(θsω)|r]=Γ1+r2π, ∀r>0,s∈R.

(10)

式(10)中:Γ(·)是Gamma函数;随机变量z(ω)是缓增的;z(θtω)关于t连续;E表示“期望”.

首先将式(1)和式(3)组成的系统转化成无噪声项的随机系统.令u=u,v=ut+εu-g(x)z(θtω),则系统(1)和系统(3)在E中等价于无噪声项的随机系统

(11)

式(11)中:

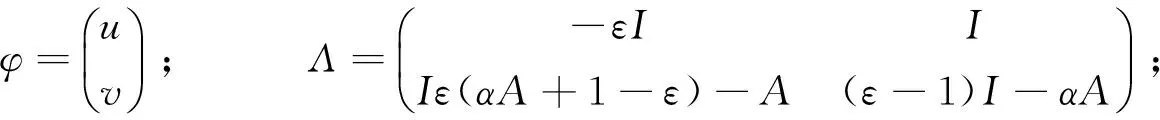
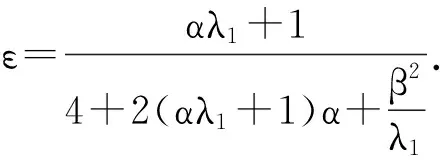
引理1 假设条件(4)成立,则对于系统(11),以下结论成立:

1)对∀ω∈Ω,系统(11)存在唯一整体解φ(t,ω,φ0)∈E,且φ(t,ω,φ0)在E中关于φ0连续,则对t≥0,ω∈Ω,解映射φ(t,ω):φ0→φ(t,ω,φ0)生成E上的连续随机动力系统{φ(t,ω)}t≥0,ω∈Ω.

2)随机动力系统{φ(t,ω)}t≥0,ω∈Ω在E中存在紧的随机吸引子A(ω),满足：A(ω)是随机紧集;A(ω)是不变的,即∀t≥0,φ(t,ω)A(ω)=A(ω);A(ω)吸引任意缓增随机集.

3)存在随机变量

(12)

使得

(13)

下面利用文献[7]中的定理2.2来估计随机吸引子A(ω)的分形维数的上界.对于ω∈Ω,取φj 0(ω)=(uj 0(ω),vj 0(ω))∈A(ω),j=1,2.设φj(t)=φ(t,0,ω,φj 0(ω))=(uj(t),vj(t)),t≥0,j=1,2,ψ(t)=φ1(t)-φ2(t)=(ξ(t),η(t)),则

(14)

(15)

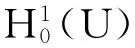
则Hn(U)×Hn(U)是E的2n维子空间.再令

(16)

定理1 假设条件(4)成立,则系统(11)的解φ(t)有下列结论：

1)对∀ω∈Ω,t≥0,存在随机变量C2(ω)>0和2n维投影算子Pn:E→PnE=Hn(U)×Hn(U),使得∀φ10,φ20∈A(ω),有

(17)

‖(I-Pn)φ(t,ω,φ10(ω))-(I-Pn)φ(t,ω,φ20(ω))‖E≤(e-σt+δne∫t0C2(θsω)ds)‖φ10-φ20‖E.

(18)

式(18)中,

(19)

2)E[C2(ω)2]<∞.

3)对∀ω∈Ω,A(ω)的分形维数有上界

(20)

式(20)中,

(21)

证明 1)令ψ(t)与式(14)作内积,可得

(22)

由文献[13]中引理4.1得

(23)

(24)

式(24)中,θ∈[0,1].综合式(22)～式(24)可得

(25)

对式(25)在[0,t](t≥0)上应用Gronwall不等式,可得

(26)

令ψn=Qnψ与式(14)作内积,可得

(27)

由式(4)、式(15)与Hölder不等式得

‖-f(u1)+f(u2)‖2=∫U[f(u2)-f(u1)]2dx=∫U[f′(u2)u2-f′(u1)u1]2dx=

∫U[(f′(u2)-f′(u1))u2+f′(u1)(u2-u1)]2dx≤∫U[c2ξu2+c1ξ]2dx≤

∫U[2(c2ξu2)2+2(c1‖‖‖ξ‖2,c3>0.

(28)

则由式(16)、式(28)得

(29)

将式(29)代入式(27)得

(30)

对式(30)在[0,t](t≥0)上应用Gronwall不等式,可得

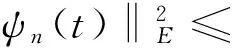
(31)

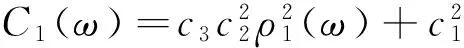
(32)

因此,由式(31)、式(32)得

(33)

2)由C2(ω) 的表达式得

(34)

利用Hölder不等式与式(10)知

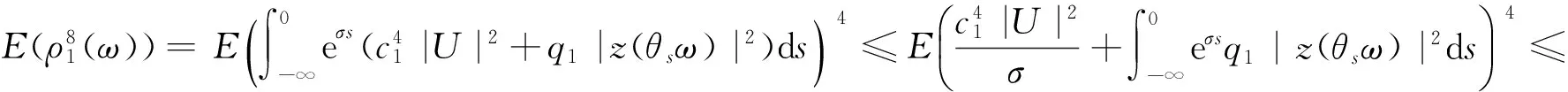
(35)

3)由式(21)得

定理1证毕.

2 带可乘噪声的随机波动方程

对满足条件(3)和(4)的方程(2)的解确定的随机动力系统的随机吸引子的分形维数上界进行估计.令u=u,v=ut+εu-cuz(θtω),ε同上节,则在E中,系统(2)和系统(3)等价于下面的系统：

(36)

由文献[13]得到下面结论:

引理2 假设条件(4)成立且

(37)

则对于系统(36),以下结论成立:

1)对∀ω∈Ω,系统(36)存在唯一整体解φ(t,ω,φ0)∈E,且φ(t,ω,φ0)在E中关于φ0连续,则对t≥0,ω∈Ω,解映射φ(t,ω):φ0→φ(t,ω,φ0)生成E中的连续随机动力系统{φ(t,ω)}t≥0,ω∈Ω.

2)随机动力系统{φ(t,ω)}t≥0,ω∈Ω在E中存在紧的随机吸引子χ(ω),并且存在缓增随机变量

使得

(38)

(39)

式(39)中,

类似于定理1,有如下定理:

定理2 假设条件(4)成立,并且c足够小,使得式(37)与

(40)

成立,则有下列结论：

1)对∀ω∈Ω,t≥0,存在随机变量C5(ω)≥0,C6(ω)≥0和2n维投影算子Pn:E→PnE,使得∀φ10,φ20∈χ(ω),系统(36)的解φ(t)满足:

(41)

‖(I-Pn)φ(t,ω,φ10(ω))-(I-Pn)φ(t,ω,φ20(ω))‖E≤(e∫t0C5(θsω)ds+δne∫t0C6(θsω)ds)‖φ10-φ20‖E.

(42)

式(42)中,δn由式(19)给出.

2)C5(ω),C6(ω) 满足条件

(43)

3)对∀ω∈Ω,χ(ω)的分形维数有上界

(44)

式(44)中:

(45)

(46)

由Young不等式与式(24)类似的方法得

(47)

对式(47)在[0,t](t≥0)上应用Gronwall不等式,可得

(48)

式(48)中,

(49)

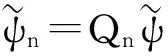
(50)

类似于式(28),由式(38)得

(51)

(52)

式(52)中:

(53)

C6(ω)=C3(ω)+12C24(ω).

(54)

2)由式(10)和式(37)得

(55)

(56)

(57)

式(57)中,

(58)

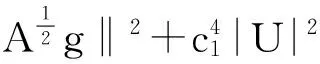
由式(40)知

由Hölder不等式与式(9)有

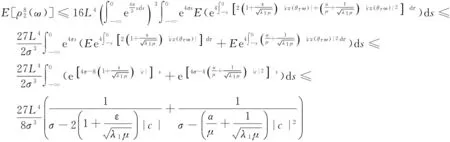
(59)

3)在式(41)和式(42)中取t=t0(见式(45)),且由式(45)得

由文献[8]定理2.8知,对于∀ω∈Ω,有

定理 2证毕.

注1 由定理2的条件可见，带可乘噪声的方程(2)的随机吸引子的分形维数的有界性要求随机项系数|c|适当小,而带可加噪声的方程(1)则没有这个限制条件,这是因为可乘噪声项与状态变量有关，而可加噪声项与状态变量无关．

[1]Lü Yan,Wang Wei.Limiting dynamics for stochastic wave equations[J].J Differential Equations,2008,244(1):1-23.

[2]Yang Meihua,Duan Jinqiao,Kloeden P.Asymptotic behavior of solutions for random wave equations with nonlinear damping and white noise[J].Nonlinear Anal Real World Appl,2011,12(1):464-478.

[3]Zhou Shengfan,Yin Fuqi,Ouyang Zigen.Random attractor for damped nonlinear wave equations with white noise[J].SIAM J Appl Dyn Syst,2005,4(4):883-903.

[4]Fan Xiaoming.Attractors for a damped stochastic wave equation of sine-Gordon type with sublinear multiplicative noise[J].Stoch Anal Appl,2006,24(4):767-793.

[5]Fan Xiaoming.Random attractors for damped stochastic wave equations with multiplicative noise[J].Internat J Math,2008,19(4):421-437.

[6]Fan Xiaoming,Wang Yaguang.Fractal dimension of attractors for a stochastic wave equation with nonlinear damping and white noise[J].Stoch Anal Appl,2007,25(2):381-396.

[7]Zhou Shengfan,Zhao Min.Fractal dimension of random invariant sets for nonautonomous random dynamical systems and random attractor for stochastic damped wave equation[J].Nonlinear Anal,2016,133:292-318.

[8]Zhou Shengfan,Zhao Min.Fractal dimension of random attractor for stochastic non-autonomous damped wave equation with linear multiplicative white noise[J].Discrete Contin Dyn Syst,2016,36(5):2887-2914.

[9]Ghidaglia J M,Marzocchi A.Longtime behavior of strongly damped nonlinear wave equations, global attractors and their dimension[J].SIAM J Math Anal,1991,22(3):879-895.

[10]Yang Meihua,Sun Chunyou.Dynamics of strongly damped wave equations in locally uniform spaces:Attractors and asymptotic regularity[J].Trans Amer Math Soc,2009,361(4):1069-1101.

[11]尹福其,周盛凡,李红艳.具强阻尼的随机sine-Gordon方程的随机吸引子存在性[J].上海大学学报:自然科学版,2006,12(3)：260-265.

[12]郝红娟,周盛凡.强阻尼随机sine-Gordon方程随机吸引子的存在性[J].上海师范大学学报:自然科学版,2010,39(2)：121-127.

[13]Wang Zhaojuan,Zhou Shengfan.Asymptotic behavior of stochastic strongly damped wave equation with multiplicative noise[J].International Journal of Modern Nonlinear Theory and Application,2015,4(3):204-214.

[14]Foias C,Olson E.Finite fractal dimension and Hölder-Lipschitz parametrization[J].Indiana Univ Math J,1996,45(3):603-616.

(责任编辑 陶立方)

On fractal dimension of random attractor for the stochastic strongly damped wave equation

ZHOU Shengfan, WANG Meng

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

It was considered the upper bound estimation of the fractal dimension of random attractors for stochastic strongly damped wave equations with additive and multiplicative white noises. Firstly, these stochastic equations with white noises was transfered into random equations with random parameters without noise terms by the Ornstein-Uhlenbeck process. Secondly, it was divided the difference between the two solutions of random equations into a sum of two parts, and estimated the norm of these two parts and the boundedness of expectation of some random variables, respectively. Finally, it was obtained the upper bound estimation formula of the fractal dimension of random attractors for the considered equations.

stochastic wave equation; random attractor; strongly damped; fractal dimension

10.16218/j.issn.1001-5051.2017.03.003

�2016-05-06；

2016-09-31

国家自然科学基金资助项目(11471290)

周盛凡(1963-),男，广西融安人，教授.研究方向:动力系统与微分方程.>

O175.25

A

1001-5051(2017)03-0258-09