浅谈单摆中等效问题的求解

刘耀华

(江西省赣州市于都中学，江西 赣州 342300)

浅谈单摆中等效问题的求解

刘耀华

(江西省赣州市于都中学，江西 赣州 342300)

单摆；等效摆长；周期；等效重力加速度

一、单摆中等效摆长问题的求解

摆长严格意义上是悬点到球心间的距离，以下图1图2图3中各摆等效摆长一定要转化为悬点到球心间的距离，可以推到单摆周期最基本的形式，分别是：

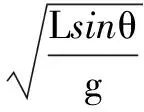
根据具体的题型变化，等效摆长应该具体分析，此时务必转化为分析物体的垂直距离，一般情况是依据数学三角函数边与角之间的关系进行换算中得到.

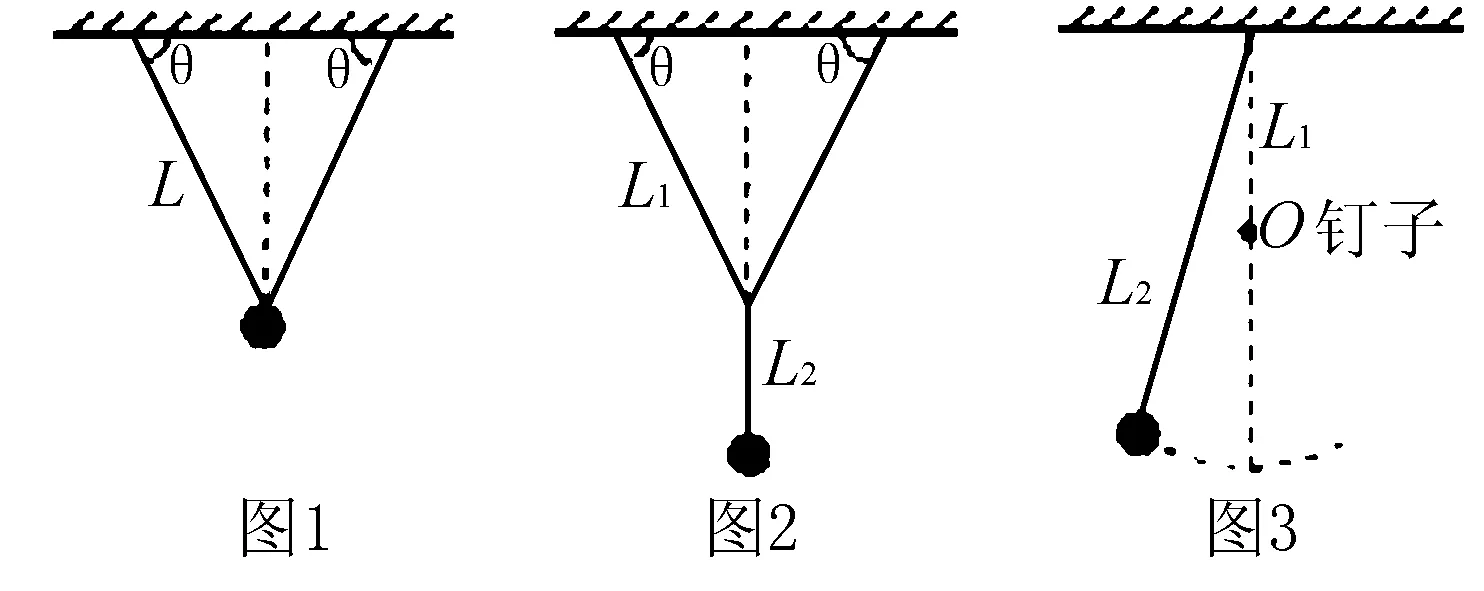
二、单摆中等效重力加速度g*问题的求解

例1 如图4所示，某具有向左匀加速运动的小车上悬挂着一单摆，其摆长为L，摆球的质量为m，求单摆的振动周期T？

解析 对摆球进行受力分析可知，摆球受到地球的重力、绳子的拉力，以及与加速度a方向相反的一个惯性力三个力的共同作用，所以，此时单摆的回复力受三个力的共同作用，且使其平衡位置偏离竖直方向O点有一个角度θ,

利用三角函数可得：

此时可得单摆的振动周期是

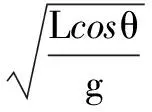
再根据小车加速度a的具体数值进行分类讨论：

①小车加速度a=0，此时θ=0，单摆的周期为：

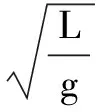
②小车的加速度增大且小车向右加速运动时，此时角度θ偏离平衡位置越大，可得周期变小.当θ=900的极限情况下，摆球在水平方向“受到”的惯性作用力f=ma》mg此时摆球不再摆动.

③小车向左做减速运动，其结果与情况②相同，只是平衡位置O’在竖直方向的左边.

点评：可见在小车中加速向左(或减速向左)，可以等效为重力加速度发生一个整体的变化，只要求出等效重力加速度，则单摆的周期问题迎刃而解.

三、单摆中等效摆长L*与等效重力加速度g*问题求解

此类问题求解单摆运动时需要同时考虑等效摆长L*和等效重力加速度g*，因为只有这样才能代入单摆的周期公式，才能转化为单摆模型.

例2 如图5(a)所示是一种记录地震装置的水平摆，摆球m固定在边长为l，质量可忽略不计的等边三角形的顶点A上，它的对边BC跟竖直线成不大的夹角α，摆球可绕固定边BC摆动，求摆球作微小摆动的周期.

解 此摆动方向在前后的竖直平面内，该等效摆长为隐形摆长如图5(b)中OA即

图5

等效重力加速度为

g*=gsinα

所以此摆做微小摆动的周期为

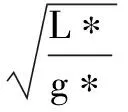
点评 此题同时考虑了单摆的等效摆长L*和等效重力加速度g*，这样转化为标准的单摆模型，很方便的求解出来，否则较为复杂，需要注意到这一点，要重视.

单摆中的等效问题主要涉及的是等效摆长L*与等效重力加速度g*，无论是将研究的物体置于变速的环境下还是在电场，磁场中，还是各种摆长的变化下，目标就是要求出等效摆长L*与等效重力加速度g*.高中物理单摆问题题型变化还是很多，但无非还是以上三种，希望同学们在做题过程中需要对单摆问题多归纳总结，这样能起到事半功倍的效果.

[1]陈盼.机械振动 机械波考点分析[J].高校招生:学科指导版,2009.

[2]陈小波.对单摆振动周期公式的讨论[J].中学教学参考,2011.

[责任编辑：闫久毅]

2017-05-01

刘耀华(1977)，男，江西于都人，本科，中学二级教师，从事高中物理教学工作．

G632

B

1008-0333(2017)19-0074-02