高中数学解题中特殊值法的应用探究

吴家美

(南京市秦淮中学，江苏 南京 211100)

高中数学解题中特殊值法的应用探究

吴家美

(南京市秦淮中学，江苏 南京 211100)

特殊值法是高中数学解题中一种常见的方法，它选取题目中的某个特殊值，通过简单的运算、推理或验证，能找到问题的正确答案或否定错误的结论，达到减缩思维过程、降低推算难度的目的.本文就此探讨了特殊值法在高中数学解题中的应用.

高中数学；解题；特殊值法；应用

“特殊值法”又名“特值法”，主要是指将某一特定量设定为特殊值，然后经过简单运算而最终得出答案的运算方法.受思维模式及经验的限制，加之数学知识本身较为系统且复杂，高中学生在接触部分数学知识很难深入抓住知识的本质及意义.数学家希尔伯特说过：“特殊化在解答数学问题中的意义更为突出.”这一提示即为在应对数学难题时，可考虑从相关特例着手，以打破常规而最终获取解决方法.总之，“特殊值法”是高中数学知识的重要参数，是学生用于解答数学的重要手段.如何强化特殊值法在高中数学解题中的应用尤为关键.

一、引入“特殊值法”，获取原题解决的关键途径

某些数学题型设计比较复杂，运算起来也相对比较困难.但其特例解决往往比较容易解决，仿效该类型解答可很快获取原题解答的关键途径.为此，在教学过程中，教师应引导学生善于仿效特例进行解答，并将解答思路迁移到原题运算中，以降低解题难度.

如下例：已知a、b、c同为正数，求证：apbqcr+aqbrcp+arbpcq≤an+bn+cn，其中r、q、p为非负整数，n∈N，且r+q+p=n.

教师可首先解剖这一道题，题干中求证的不等式较为复杂，很难从正面进行求证.为此，应考虑从特例解答着手，代入某些具体数值进行运算，如r为0、q为1、p为2.此时不等式则可表达为c2a+a2b+b2c≤a3+b3+c3，至此教师可引导学生采用“平均值不等式”进行解答证明：

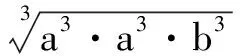
将上述三式相加可得c2a+a2b+b2c≤a3+b3+c3，运算起来相对比较简单.

而在证明一般问题时，同样可仿照上述特例进行解答，最终导出“均值不等式”验证：

apbqcrapbqcr，

arbpcq，

arbpcq

将上述三式相加可最终得apbqcr+aqbrcp+arbpcq≤an+bn+cn.

二、引入“特殊值法”，解答选择题

在解答选择题时，引出“特殊值法”，通过简答的推理、运算及验证，可排除某些错误答案或获取正确答案，以降低运算难度、降低思维转换.总之，“特殊值法”适用于可减少解题经过的问题，尤其为选择题，可达事半功倍、出奇制胜之效果.

如:在等比数列{an}各项均为正数，已知a6a5=9，求loga1+loga2+loga3+…+loga10=( ).

A.12+log3a5B.8 C.12 D.10

题意分析 在该类选择题解答过程中，考虑引入“特殊值法”可大大降低运算难度，减少计算用时.根据题干信息，可将an设定为3，然后以此进行计算，便可获取答案D.数列3，3，…满足题干条件，并具备等比数列的性质，因而在应对类似选择题可引入特殊值法，但值得注意的是不可将其迁移用于解答题的运算中，否则犯逻辑错误.

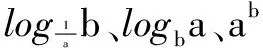
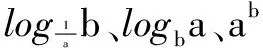
数学学科知识较为系统且复杂，在实际运算中需经大脑逻辑思维重组信息，由已知条件进行推理、运算.然而，高中生虽日常学习中不断积累知识及经验，但在应对较为复杂的题型时，往往不能很快转换思维，不知从何入手解答.本文以上述两个例题进行分析，在复杂选择题解答中，应提升学生善于运用“特殊值法”运算的能力，潜意识里对“特殊值法”有充分的认识，并在实践运算中不断总结出自我经验，哪类题型、哪个知识点中应如何代入特殊值，并提升运算准确率都需要学生逐步形成知识框架.

总之，高中学生在成长与发展都会经历从“特殊”到“一般”的过程，尤其表现为数学学习及研究中.“特殊化”是数学问题解答的有效手段，更是获取数学真理的可行工具.无论是解答选择题，还是作答填空题，引入“特殊值法”都可化抽象为具象，使整个题干更加清晰明了，对降低难度、培养学生创新及逻辑思维能力都有积极的现实意义.为此，积极引入“特殊值法”教学成为高中数学教师的重点任务.

[1]姚开成.用“特殊值法”解题举例[J].新疆石油教育学院学报，1997(02).

[2]用特殊值法解数学题[J].青海师专学报·教育科学,2003(06).

[责任编辑：杨惠民]

2017-05-01

吴家美(1971.2-)女，江苏南京人，中学一级教师，本科，从事学科教学.

G632

B

1008-0333(2017)19-0047-02