基于局部线性模型树模型的柴油机进气系统漏气和堵塞故障诊断

王英敏， 崔涛， 张付军， 董天普

(1.北京理工大学 机械与车辆学院, 北京 100081; 2.河北工程大学 水电学院， 河北 邯郸 310027)

基于局部线性模型树模型的柴油机进气系统漏气和堵塞故障诊断

王英敏1,2， 崔涛1， 张付军1， 董天普1

(1.北京理工大学 机械与车辆学院, 北京 100081; 2.河北工程大学 水电学院， 河北 邯郸 310027)

柴油机进气系统漏气和堵塞等性能退化型故障将会导致排放恶化和经济性下降。针对进气系统具有较强的非线性，难以建立精确的数学模型问题，提出基于局部线性模型树(LOLIMOT)模型的故障诊断方法，为在线故障诊断提供一种思路。提取进气压力波的一次谐波信号幅值与相位、充量系数为故障特征，采用 LOLIMOT方法对充量系数、进气压力波动幅值与相位信号建立基于发动机转速和进气密度的参考模型；采用奇偶方程生成3个残差信号，计算各个残差信号的阈值；分析残差信号和故障类型的映射关系。结果表明：所建进气压力波动幅值LOLIMOT模型、进气压力波动相位LOLIMOT模型、充量系数模型验证数据与模型仿真数据具有较高线性相关度；采用充量系数、进气压力波幅值与相位为故障特征值建立的LOLIMOT模型生成残差信号的故障诊断方法，可诊断进气系统漏气故障和中冷器堵塞故障。

动力机械工程； 进气系统； 性能退化型故障； 局部线性模型树； 故障诊断

0 引言

随着人们对保护环境的要求日益迫切，国内外排放法规强制要求对发动机排放相关的故障及时检测和维修[1]。柴油机进气系统的工作状态直接影响缸内燃烧的状态，当进气系统发生故障时，会导致经济性下降和排放性能恶化。国家标准 GB17691—2005和GB18352.3—2005 均强制要求对发动机的排放相关故障进行及时检测和维修[2]。因此，针对进气系统的故障诊断是十分必要的。

柴油机进气系统故障主要包括进气流量传感器故障、进气压力传感器故障、进气系统漏气故障和进气歧管堵塞故障等。针对传感器故障，主要采用基于解析模型的方法[3-4]、基于检测滤波器的方法[5-6]和基于神经网络的方法[7-8]。而针对漏气和堵塞等性能退化型故障目前研究较少，Nyberg等[9]提出基于解析模型的方法对柴油机进气系统漏气故障进行了诊断。Vinsonneau等[10]在改进模型的基础上，进行故障诊断。Svärd等[11]在2013年又提出基于故障模型和数据驱动的诊断方法，对漏气和堵塞故障进行了诊断。上述基于模型的方法，对解析模型依赖程度强，且只针对特种工况下的故障，可移植性不高[12]。

柴油机本身是一个复杂的非线性系统，不易建立精确的数学模型。而之前的基于振动信号或模型[9]的方法无法进行在线应用。本文提出的故障诊断方法为在线诊断提供了一种思路。局部线性模型树(LOLIMOT)可针对非线性系统建模。本文采用基于LOLIMOT的方法对柴油机进气系统充量系数和进气压力波提取的特征信号进行建模，采用信号模型不依赖于系统解析模型；采用奇偶方程法产生残差信号，并对残差信号进行统计学分析，确定残差阈值范围；并对DEUTZ6V2015增压柴油机的进气系统漏气和堵塞故障进行了诊断。

1 LOLIMOT模型介绍

LOLIMOT算法首次被Nelles提出，Pedram 等证明了在研究非线性系统和模式识别方面LOLIMOT算法与其他神经网络相比是一种更有效的网络。

LOLIMOT的网络结构如图1所示，LOLIMOT的输出是将常用的径向基函数神经网络的输出层权值用输入的线性函数代替。其工作空间按二叉树算法被分成M个子空间，每个子空间代表一个局部模型。图1中：u1和u2为LOLIMOT输入;φi，i=1,2,3，…，M，为第i个局部模型的权重函数，决定每个局部模型的有效区间及局部模型之间的过渡关系;yi，i=1,2,3，…，M,为第i个局部模型的输出模型;y为LOLIMOT输出, 是M个局部模型的加权和。

图1 LOLIMOT的网络结构Fig.1 Network structure of LOLIMOT

LOLIMOT的训练也是通过二叉树进行的，以输入空间为两维，迭代4次为例，分割过程如图2所示。LOLIMOT方法将输入空间即工作空间看成超矩形，每次迭代将输入空间形成的超矩形按二叉树重新划分，每次分割有两种分法，从中选择训练误差最小的一种划分作为新的超矩形，每个超矩形代表一个局部模型。

图2 LOLIMOT的4次迭代过程示意图Fig.2 Four iterations of LOLIMOT algorithm

国内外学者利用LOLIMOT在不同领域已取得了一些研究成果。Petchinathan等[13]在2014年将LOLIMOT算法用于非线性系统识别。Lucas等[14]在2012年将LOLIMOT算法用于地下空洞的估计。王新宇等[15]在2015年将LOLIMOT算法用于柴油机高压共轨排放模型的建立。Kolewe等[16]在2015年采用LOLIMOT算法对柴油机排气流量进行估计。逄红[17]采用LOLIMOT算法对发动机排放、扭矩和经济性建模，避免了基于脉谱图(MAP)控制方法上的复杂性。Sequenz[18]采用LOLIMOT算法建立排放模型，并指出LOLIMOT方法在算法复杂性和时间上比常规方法例如常规MAP标定法、一种核方法和自适应多项式拟合等方法具有一定优越性。

2 基于LOLIMOT模型的故障诊断系统

基于模型诊断的基本思想就是，利用系统内部结构、行为或功能模型来预测系统行为，并将这些模型预测值与系统观测值进行比较。基于模型的柴油机故障诊断模块主要包括模型、残差生成器和判别准则三部分。本文中诊断系统如图3所示，故障包括柴油机故障，不考虑执行器和传感器故障，参考模型采用LOLIMOT模型；残差生成器采用奇偶方程法[19]；故障诊断识别采用基于残差阈值方法的判定规则。

图3 基于模型的故障诊断框架Fig.3 Fault diagnosis scheme based on model

2.1 进气系统模型的建立

进气系统建模采用半物理仿真方法和LOLIMOT建模方法。半物理仿真法采用平均值模型建模，不考虑循环内的变化，认为进气系统是一个理想的开口系统。根据速度- 密度法，可得到进入气缸的空气质量流量为

(1)

式中：Vd为气缸排量(m3)；R为空气的气体常数，R=287 J/(kg·K)；Ti为进气温度；ΦC为充量系数；pi为进气压力；n为发动机转速。

(2)

在以往的研究中，ΦC一般通过查基于发动机转速和进气歧管压力的稳态MAP得到。而本研究中，考虑到进气系统中温度对进气状态的影响，为了更好体现热交换、气体回流等非线性现象。采用LOLIMOT对ΦC建立基于发动机转速和进气密度的模型。

ΦC≈fΦC(n,ρi)，

(3)

(4)

式中：ρi为进气密度，采用理想气体方程通过进气压力和温度计算得到。

当故障发生时，对进气压力影响明显[5-7]。进气压力的波动受到气缸工作循环的影响。由于进气系统内的气体，可以认为是应力、应变呈正比的牛顿流体，进气系统内的气体的运动，可视为弹性系统在外激振力作用下的受迫振动。因此，进气压力波动也将是以发动机的工作循环为周期的。从角域分析，对于六缸四冲程柴油机来说，其波动周期为120°. 发动机转速为1 300 r/min，扭矩在1 100 N·m工况下，采用洛阳南峰机电设备制造有限公司生产的440 kW电涡流测功机和瑞士奇石乐公司生产的DEWE-3010燃烧分析仪，每0.2°CA采集一次进气压力，测量结果如图4所示。本文中进气压力可近似为一个平均幅值和一个一次谐波。

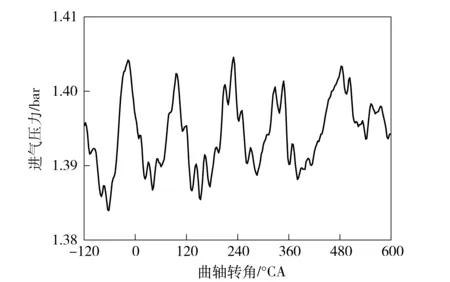
图4 进气压力波形图Fig.4 Waveform of intake pressure

进气压力可近似表示为

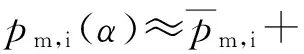
(5)

分别对进气压力的幅值和初始相位用LOLIMOT算法建模，

Apm,i≈fApm,i(n,ρi),

(6)

φpm,i≈fφpm,i(n,ρi),

(7)

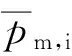
2.2 残差的生成

利用上面所建立的信号模型，采用奇偶方程方法生成3个残差。具体为

rΦC=ΦC-fΦC(n,ρi)，

(8)

rApm,i=Apm,i-fApm,i(n,ρi)，

(9)

rφpm,i=φpm,i-fφpm,i(n,ρi).

(10)

3 柴油机进气系统故障诊断LOLIMOT信号模型

3.1 柴油机进气系统故障诊断系统诊断试验

图5 DEUTZ-BF6M1015C涡轮增压柴油机台架Fig.5 DEUTZ-BF6M1015C turbocharged diesel engine

图5为本文所采用的增压柴油机台架试验，台架试验以DEUTZ-BF6M1015C发动机为诊断对象，采用440 kW电涡流测功机和DEWE-3010燃烧分析仪，可基于角度或时间采集气缸压力、进气压力、排气压力和瞬时转速等工况数据。从电子控制单元中可获取的参数有环境压力、环境温度和进气压力、进气温度、进气流量等。

表1为DEUTZ-BF6M1015C发动机的主要技术参数。

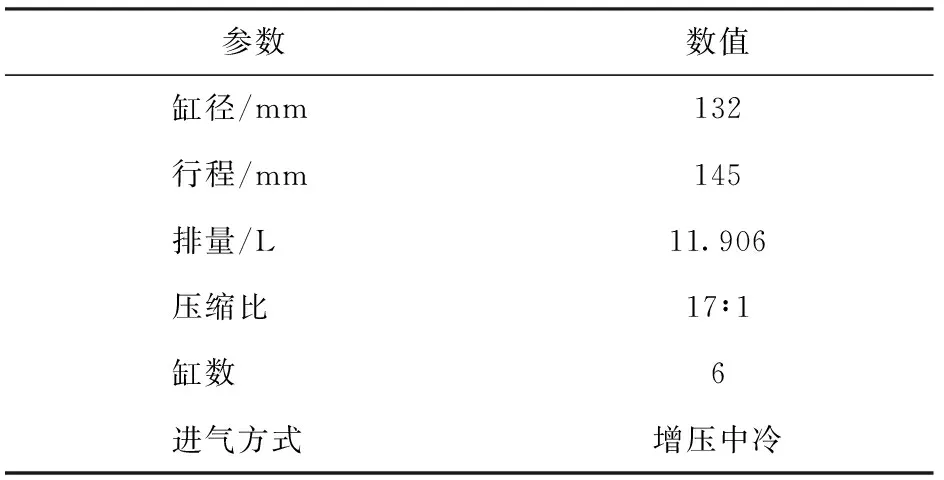
表1 发动机技术参数

由于台架试验条件限制，LOLIMOT模型所需的数据提取过程存在干扰。本文中对故障设置采用发动机性能仿真软件GT-Power对柴油机进行建模，在模型上进行仿真实验。韩恺等根据柴油机台架试验数据建立模型如图6所示。并对柴油机模型的燃烧过程、进排气系统和整体性能进行了校验，误差都在5%以内[20]，符合模拟计算需求，可用于柴油机故障诊断验证。

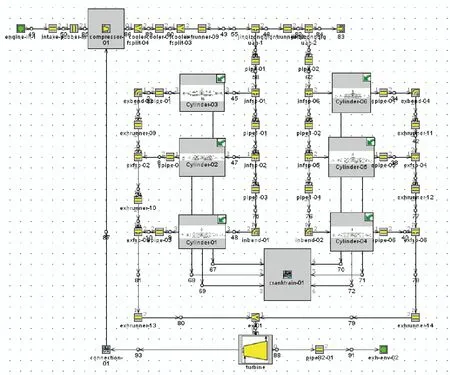
图6 DEUTZ-BF6M1015C涡轮增压柴油机仿真模型Fig.6 Simulation model of DEUTZ-BF6M1015C turbocharged diesel engine

本文在所建柴油机模型上选取1 000 r/min、1 300 r/min、1 500 r/min、1 700 r/min和1 900 r/min共5组能够覆盖DEUTZ-BF6M1015C柴油机主要工况范围的转速，并在每组转速下扭矩开始点为200 N·m、每200 N·m选择一个稳态工况点，最大直到外特性点获取学习实验数据。在1 400 r/min和1 800 r/min两组典型转速下,负荷分别为10%、25%、50%、75%和100% 5个稳态工况下获取验证数据。如图7所示，所取学习实验数据能代表发动机主要工况，验证数据代表典型工况。其中：圆圈“○”表示学习实验数据，用来建立LOLIMOT参考模型；三角“△”表示验证数据，用来验证所建立的参考模型准确性；实心方框“■”为发动机外特性工况点。

图7 DEUTZ-BF6M1015C涡轮增压柴油机仿真模型实验数据和验证数据Fig.7 Experimental and test data

3.2 进气系统LOLIMOT建模结果分析

采用LOLIMOT算法建模时，编程时定义maximp为阈值，当每次划分全局误差降低值小于阈值时，训练结束，本实验设置为5%.

3.2.1 进气压力波动幅值模型

进气压力波动幅值建模以发动机转速和进气密度作为输入，采用学习数据建模,验证数据对模型验证。

如图8所示，超平面分割11次后，全局误差符合要求，迭代停止，分割停止共12个超平面。图9为11次迭代过程。

图8 进气压力波动幅值训练全局误差Fig.8 Global training error of air inlet pressure fluctuation amplitude

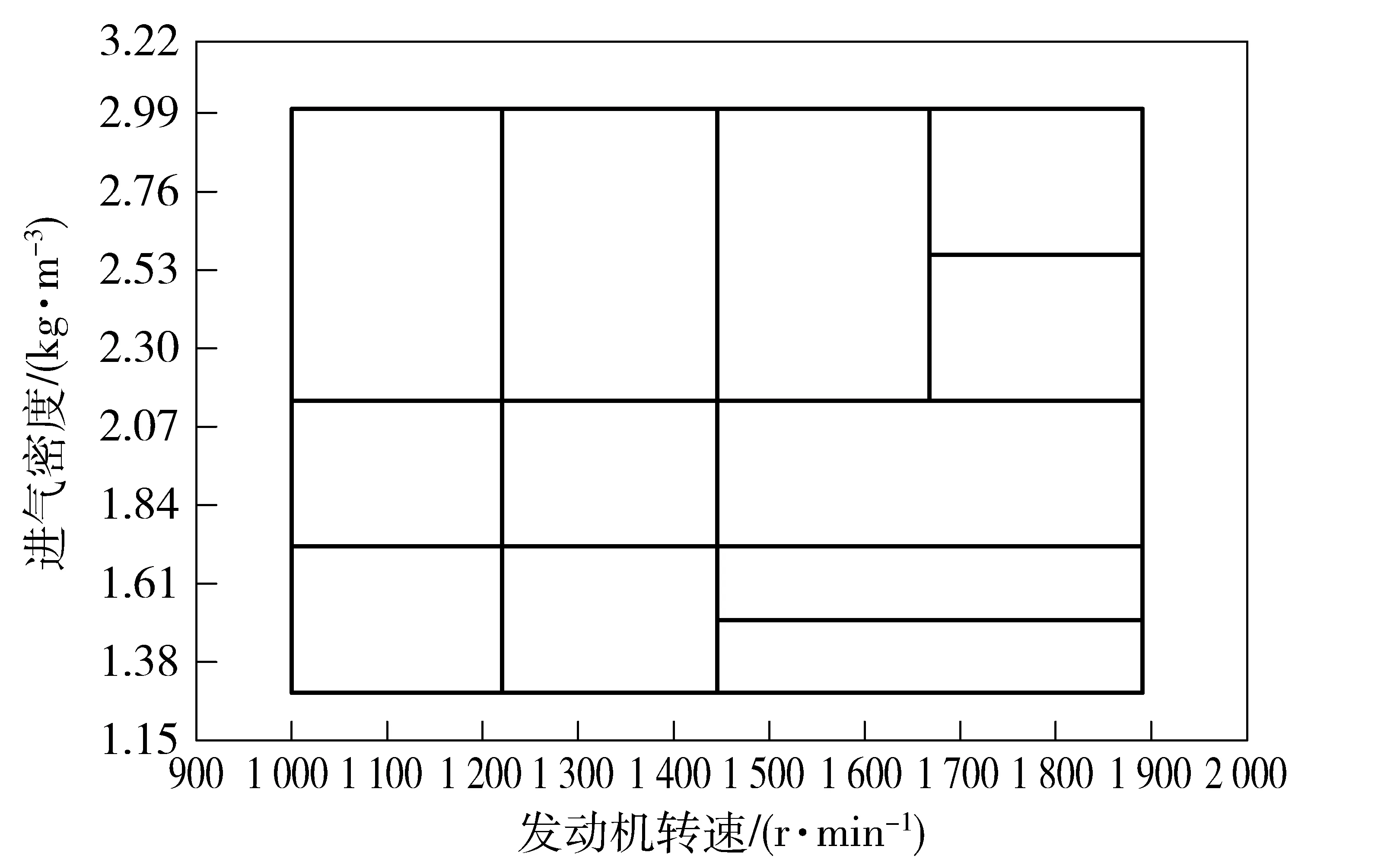
图9 LOLIMOT算法的11次迭代过程Fig.9 Eleven iterations of LOLIMOT algorithm

为了评估所建进气压力波动模型和实验结果之间的准确性，采用统计学概念，线性相关系数R2和平均相对误差A. 当线性相关系数R2越接近1，平均相对误差越小，则说明两数值的相关度越强[21-22]。

采用图7中所示的验证数据，得到模型数据和实验值如图10所示，进气压力幅值的实验值和模型输出值的线性相关系数R2达到98.7%，实验值和模型输出值的平均相对误差A为6.6%.

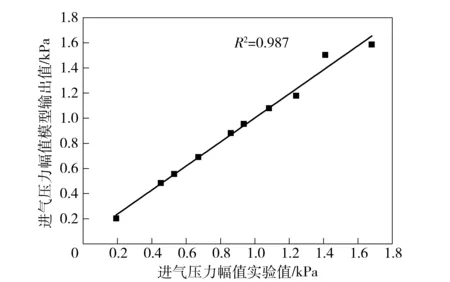
图10 进气压力幅值线性回归Fig.10 Experimental and test data of linear regression coefficient of intake pressure amplitude

图11为LOLIMOT算法所建进气压力波动幅值参考模型，表明进气压力波动幅值变化与转速变化呈近似线性变化；在低转速时，受密度影响较小，幅值波动较小；而在高转速时受密度影响较大。因此，在相同转速下,不同负荷时,进气压力波动的规律相近,负荷越大,进气压力的波动范围也越大；随着转速的变化,波动强度也是随转速波动变化的[23]。

图11 进气压力波动幅值LOLIMOT模型Fig.11 Reference model of intake pressure amplitude

3.2.2 进气压力波动相位模型

进气压力波动幅值建模以发动机转速和进气密度作为输入。如图12所示，经过14次分割后，全局误差达到要求，分割停止。图13为14次迭代过程。

图12 DEUTZ-BF6M1015C涡轮增压柴油机仿真模型实验数据和验证数据进气压力波动相位训练全局误差Fig.12 Experimental and test data of global training error of intake pressure fluctuation phase

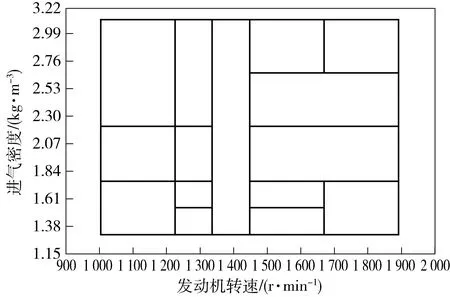
图13 LOLIMOT算法的14次迭代过程Fig.13 Fourteen iterations of LOLIMOT algorithm

如图14所示，采用图7中验证数据对所建模型进行验证，进气压力相位的实验值和模型输出值的线性相关系数R2为97.8%，平均相对误差A为5.4%.

图14 进气压力相位线性回归Fig.14 Experimental and test data of linear regression coefficient of intake pressure phase

图15为LOLIMOT算法所建进气压力波动相位参考模型，表明随着发动机转速增加，进气压力波动相位角度增加。主要是由于发动机进气波动按照当地因素在进气管中传播，由于密度变化较小，波动速度变化不大，所以密度对相位角影响较小。因此进气压力波动相位与转速近似成线性关系[24]。

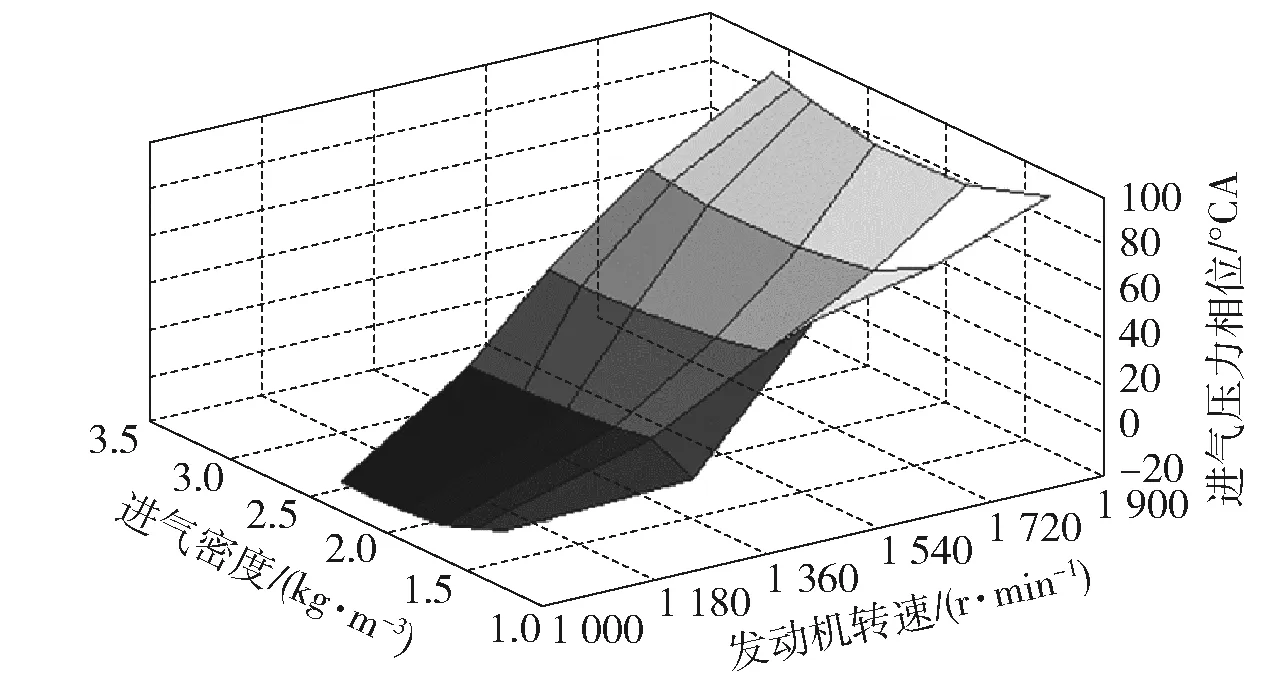
图15 进气压力波动相位LOLIMOT模型Fig.15 Reference model of intake pressure phase

3.2.3 充量系数模型

充量系数建模以发动机转速和进气密度作为输入。图16显示了分割9次时，此时全局误差达到试验要求，分割停止，共分成了10个超平面。

图16 LOLIMOT算法的9次迭代过程Fig.16 Nine iterations of LOLIMOT algorithm

图17显示充量系数验证数据的实验值和模型输出值的线性相关系数R2达到97.8%，实验值和模型输出值的平均相对误差A为4%.

图17 充量系数线性回归Fig.17 Linear regression coefficient of volumetric efficiency

图18为LOLIMOT算法所建充量系数参考模型，充量系数随着转速的增大而增大。

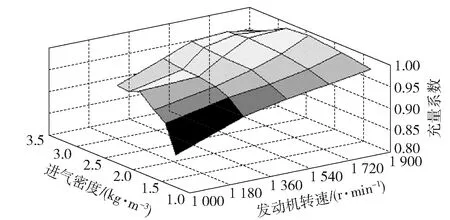
图18 充量系数LOLIMOT模型Fig.18 Reference model of volumetric efficiency

4 柴油机进气系统故障诊断

4.1 故障诊断阈值的确定

在故障诊断系统中，阈值的设定直接影响故障诊断的成败。如果阈值设置过低，则会出现误诊断；如果阈值设置过高，则会出现漏诊断。阈值设定的合理性直接影响故障诊断系统的可靠性。

在理想状态下，无故障时残差信号为0，有故障时残差值为非零。在实际中，由于信号采集过程中噪声的影响和建模误差的影响，无故障状态时，残差信号并不为0. 因此本文中通过统计分析转速无故障工况下10组残差数据，每组100个数据。以其中1组进气压力波动幅值误差数据分析，如图19所示，残差频率分布直方图为进气压力波动幅值在无故障时的残差分布情况。

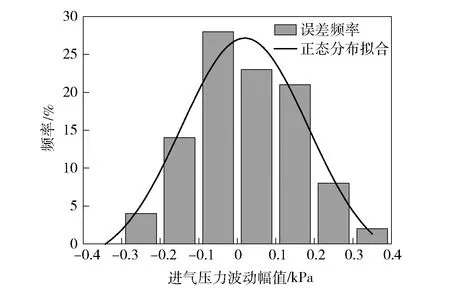
图19 进气压力波动幅值残差频率分布直方图Fig.19 Residual distribution histogram of intake pressure fluctuation amplitudes

通过图20发现，数据元素都分布在对角线两侧，逼近对角线，表明其残差分布符合正态分布，其中数学期望μ=0.022 2，标准差σ=0.136 7.

图20 进气压力波动幅值残差Q-Q图Fig.20 Q-Q diagram of residual errors of intake pressure fluctuation amplitude

经过分析发现10组残差信号的频率分布符合正态分布，设置信区间为95%，分别求得每组残差信号的置信区间并设置阈值上下限。本文中所得阈值如表2所示。由于无故障时，进气压力计算波动幅值计算在0.2 kPa. 根据故障出现时，超出阈值情况结合实际传感器的测量精度，本文中进气压力波动幅值可设置为1 kPa.

表2 故障诊断阈值

4.2 故障诊断结果分析

4.2.1 故障设置及残差分析

本文设置中冷器到气缸之间的漏气故障和中冷器堵塞故障。如图21所示为发动机故障设置部位，其中pi和Ti为进气压力和进气温度，在图21中红色线标志位置设置漏气故障直径为3 mm和5 mm,中冷器堵塞20%和30%. 本文中考虑的是中冷器之后到气缸之间的漏气现象，采用漏气直径3 mm、5 mm进行建模表示了漏气的严重程度。中冷器堵塞20%和30%分别表示中冷器堵塞严重程度。本文中5 mm漏气故障对柴油机发动机性能影响较为明显[9]，该工况下30%堵塞已经造成进气量减少近7%，对柴油机性能影响较明显。当然故障越早发现越好，因此本文针对不同程度的故障进行诊断研究。

图21 发动机故障设置Fig.21 Fault setting of engine

通过修改仿真模型中冷却器元件模块，修改Number of Identical Pipes项目中的参数，可完成对冷却器堵塞故障设置。例如本文模拟了中冷器堵30%故障，具体从Number of Identical Pipes项目中的数值3 000改为2 100；通过进气管道设置Flowsplitright模块和throttleConn模块，设置漏气直径为5 mm，通过运行模型获得有效参数。

由于随着故障的严重程度，故障特征信号强度越明显。在发动机转速1 300 r/min、扭矩1 100 N·m工况下，中冷器在堵塞20%和30%时进气压力幅值残差近似正态分布，其分布如图22所示。中冷器堵塞20%时的残差分布大约在[-1.2 kPa -0.5 kPa]区间内，中冷器堵塞30%时残差分布大约在[-1.7 kPa -1.2 kPa]区间内。按表2中的进气压力幅值波动阈值[-1 kPa 1 kPa]，则中冷器堵塞20%故障诊断容易出现漏诊断，而中冷器堵塞30%时，误诊断和漏诊断率较低。通过残差频率密度分布，可知针对堵塞30%的故障具有较高诊断率。同样，在兼顾误诊断率和漏诊断率都较低的情况下。同样，漏气直径由小变大时的残差分析方法类似。由于篇幅有限，针对其他残差结果并未列出。通过分析误差分布，本文针对5 mm漏气故障和30%的中冷器堵塞故障具有较高的诊断率。

图22 转速1 300 r/min、扭矩1 100 N·m 工况下堵塞程度不同时的残差频率分布密度直方图Fig.22 Residual distribution histograms in different blockages at 1 300 r/min and 1 100 N·m

4.2.2 漏气故障

在发动机转速1 300 r/min、扭矩1 100 N·m工况下，漏气直径为5 mm. 每0.2°CA采集一次进气压力, 在20～22 s间设置漏气故障，采集进气压力值并进行拟合。图23所示为正常时进气压力拟合波形和漏气故障时进气压力拟合波形。从中提取压力波动幅值和相位，并与所建模型比较，得出残差信号。

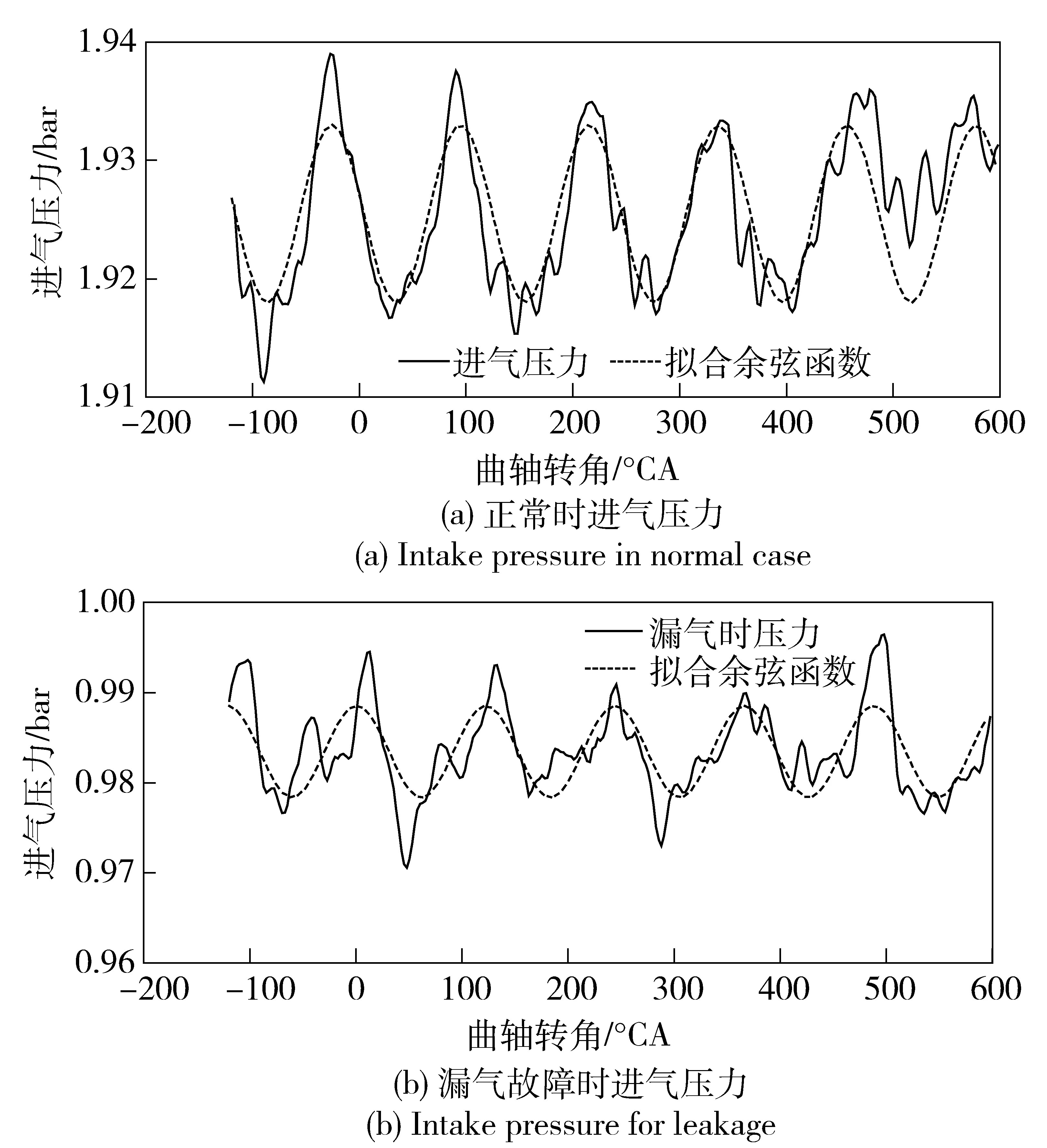
图23 转速1 300 r/min、扭矩1 100 N·m工况下的进气压力Fig.23 Intake pressure at 1 300 r/min and 1 100 N·m

图24为漏气故障发生时残差诊断图。进气歧管漏气故障发生时，充量系数残差值超出正常阈值范围。由于管道漏气，进气压力减小，进入气缸气体量减小，充量系数减小。进气压力波动幅值和相位的残差值还在正常范围，故障对其进气压力波动影响较小。

图24 转速1 300 r/min、扭矩1 100 N·m 工况下的漏气故障诊断Fig.24 Residual detection on leakage at 1 300 r/min and 1 100 N·m

4.2.3 堵塞故障

在发动机转速1 300 r/min、扭矩1 100 N·m工况下，设置在中冷器和气缸之间设置堵塞故障，每0.2°CA采集一次进气压力, 在20～20 s间设置漏气故障，故障诊断结果如图25所示。

图25 转速1 300 r/min、扭矩1 100 N·m 工况下的堵塞故障诊断Fig.25 Diagnosis of blocking fault at 1 300 r/min and 1 100 N·m

在进气系统中冷器堵塞故障发生时，充量系数残差值还在正常阈值范围。由于进气歧管堵塞，进气压力增大，进入气缸气体量增大，因此充量系数增大，但其残差值变化幅度较小。而故障对其进气压力波动影响较大，进气压力波动幅值残差减小，相位的残差值增大。

4.3 故障识别

通过实验分析可得到故障状态和残差值之间的映射关系，表3为进气系统故障和残差值的映射关系。

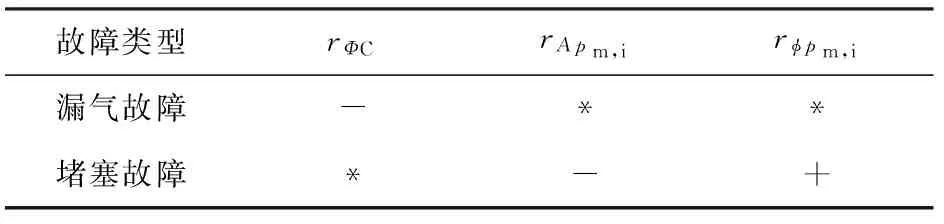
表3 故障和残差值的映射关系

注：“-”表示残差值和故障负相关，“+”表示残差值和故障正相关，“*”表示残差值与故障无关。根据所得故障类型和残差的映射关系，充量系数残差信号可以诊断漏气故障，进气压力波动的幅值信号和相位信号残差可以诊断堵塞故障。

本文中采用模糊判定规则，具体规则如下：

1)如果D(rΦC)=-1，且D(rApm,i)=0和D(rφpm,i)=0，则进气歧管漏气故障发生。

2)如果D(rApm,i)=-1且D(rφpm,i)=1，D(rΦC)=0，则进气歧管堵塞故障发生。

(11)

式中；di+是阈值上限，di-是阈值下限。

4.4 故障诊断算法的在线实现

4.4.1 传感器采样

本文试验中采用DEWE-3100燃烧分析仪，可基于角度或时间采集进气压力，每0.2°CA采集一次进气压力，在模型仿真计算时也采用该采样频率。目前，真实车用传感器大部分是基于时间进行采集的。而德国BOSCH公司的进气压力传感器既可以基于时间采集也可以通过相位进行采集。通过控制器设置同步相位采集。而在线故障诊断需考虑传感器的响应和精度，目前常用的BOSCH公司进气压力传感器，其响应时间小于2 ms,采样频率为500 Hz左右。而本文中每0.2°CA采集一次进气压力,其采样频率较高。Kistler传感器可满足其精度和响应要求，但是由于其价格较高，不适宜批量生产。

通过进一步分析，如图26为转速1 300 r/min外特性工况下的进气压力波动，黑色为每2.5°CA采集的数据，红色为0.2°CA采集的数据。发现每2.5°CA采集一次进气压力也能精确提取进气压力波动的幅值，拟合出一次谐波波形的幅值精度在0.000 1 kPa，不影响该故障诊断方法使用。

图26 转速1 300 r/min外特性时不同采样时间间隔的进气压力波形图Fig.26 Intake pressure waveforms at different sampling intervals at 1 300 r/min

图27为转速1 300 r/min外特性工况下,采样时间间隔分别为2.5°CA和0.2°CA时，采集数据的进气压力升高率与累积频率分布图。由图27可知，不同压力升高率对应的累积频率分布近似一致，因此，在这两种不同采样时间间隔时，可以有效提取波形特征。

图27 转速1 300 r/min外特性时不同采样时间间隔的进气压力升高率Fig.27 Cumulative frequency of pressure rise rates at different sampling intervals at 1 300 r/min

图28为不同采样时间间隔，得到的进气最大压力升高率随循环数变化，也呈近似一致的波动规律，二者的偏差在±6.8%之内，每2.5°CA采集一次进气压力与每0.2°CA采集一次进气压力得到一致的进气最大压力升高率。

图28 转速1 300 r/min外特性时不同采样时间间隔的进气最大压力升高率Fig.28 Maximum intake pressure rise rates at different sampling intervals at 1 300 r/min

因此，在线诊断可选用频率为6 kHz左右、价格合适的压阻式进气压力传感器，考虑到计算机采集及提取幅值相位的响应时间，可增加峰值保持电路，采用积分方法提取幅值。减少计算量，提高响应速度，可解决精度问题。

4.4.2 算法复杂度

在线故障诊断要求算法简单易实现，本文采用大量的离线数据进行处理提取特征，通过局部线性模型建立参考模型，所建LOLIMOT模型可以转化成MAP，所生成充量系数、进气压力波动幅值和相位的参考模型可相应转化为MAP. 生成的参考MAP放入在线故障诊断算法中，加上少量在线模型，可减小在线算法的复杂度。

由于LOLIMOT模型是一种神经网络模型，输入输出之间是非线性的关系。而直接MAP法是一种线性插值法。LOLIMOT模型能更好地体现系统特征，数据采集可采用动态和静态数据，且需要数据量比MAP标定要小[17]。

5 结论

1)本文提出基于LOLIMOT模型的故障诊断方法，分析进气压力波动信号，提取其波动相位、幅值和充量系数3个参数，反映柴油机进气系统本质特性。

2)采用LOLIMOT法对故障特征参数建模，将进气压力波动幅值、进气压力波动相位和充量系数表示成发动机转速和进气密度的模型。仿真结果表明，模型验证数据和模型仿真数据具有较高的线性相关度，3个参数的线性相关度系数R2分别为98.7%、97.8%和97.8%.

3)分析残差频率分布直方图和Q-Q图，表明残差符合正态分布，设置95%的置信区间，确定各个残差的合理阈值。研究结果表明，充量系数残差可诊断漏气故障，而进气压力幅值和相位可诊断堵塞故障。

4)本文提出的故障诊断方法为实际在线诊断算法提供了一种解决思路。通过传感器的采样设计和LOLIMOT算法的简化，为故障诊断算法的在线应用提供了途径。

References)

[1] Sidorow A, Isermann R, Cianflone F, et al. Model based fault detection of the air and exhaust path of diesel engines including turbocharger models[C]∥SAE 2011 World Congress & Exhibition. Detroit, MI, US: SAE, 2011.

[2] 周兴利.电控柴油机故障智能诊断研究[D]. 上海：上海交通大学,2007:3-4. ZHOU Xing-li. Study of intelligence diagnosis for electronic controlled diesel engine faults[D]. Shanghai: Shanghai Jiao Tong University, 2007:3-4. (in Chinese)

[3] Pourbabaee B, Meskin N, Khorasani K. Sensor fault detection, isolation, and identification using multiple-model-based hybrid Kalman filter for gas turbine engines[J]. IEEE Transactions on Control Systems Technology, 2016, 24(4):1184-1200.

[4] 荣吉利. 基于模型的航天器在轨传感器故障诊断方法[J]. 兵工学报, 2002, 23(2):242-245. RONG Ji-li. A model-based onboard fault diagnosis for spacecraft sensors[J]. Acta Armamentarii, 2002, 23(2):242-245. (in Chinese)

[5] 孙云龙,刘波澜,崔涛，等.基于模型的柴油机进气系统故障诊断方法研究[J].车用发动机,2013(3):84-87. SUN Yun-long, LIU Bo-lan, CUI Tao, et al. Model-based fault diagnosis method of diesel engine intake system[J]. Vehicle Engine, 2013(3):84-87. (in Chinese)

[6] Rissoni G, Min P. Detection of sensor failures in automotive engines[J].IEEE Transactions on Vehicular Technology, 1991, 40(2): 487-500.

[7] Hamad A, Yu D, Gomm J B, et al. Radial basis function neural network in fault detection of automotive engines[J]. International Journal of Engineering Science & Technology,2010, 2(10):1-8.

[8] Cook W R, Kepes F, Joseleau-Petit D, et al. Dynamic fault detection and isolation for automotive engine air path by independent neural network model[J]. International Journal of Engine Research, 2012, 15(1):87-100.

[9] Nyberg M, Perkovic A. Model based diagnosis of leaks in the air-intake system of an SI-engine[C]∥SAE International Congress and Exposition. Detroit, MI, US: SAE, 1998.

[10] Vinsonneau J A F, Shields D N, King P J, et al. Improved SI engine modelling techniques with application to fault detection[C]∥International Conference on Control Applications. Glasgow, Scotland: IEEE, 2002:719-724.

[11] Svärd C, Nyberg M, Frisk E, et al. Automotive engine FDI by application of an automated model-based and data-driven design methodology[J]. Control Engineering Practice, 2013, 21(4):455-472.

[12] Duyar A, Eldem V, Merrill W. Fault detection and diagnosis in propulsion systems: a fault parameter estimation approach[J]. AIAA Journal of Guidance, Control and Dynamics, 1994, 17(1):104-108.

[13] Petchinathan G, Valarmathi K, Devaraj D, et al. Local linear model tree and neuro-fuzzy system for modelling and control of an experimental pH neutralization process[J]. Brazilian Journal of Chemical Engineering, 2014, 31(2):483-495.

[14] Lucas C, Hajian A, Zomorrodian H, et al. Depth estimation of cavities from microgravity data using a new approach: the local linear model tree (LOLIMOT)[J]. Near Surface Geophysics, 2012, 10(3):221-234.

[15] 王新宇, 何超, 李加强,等. 基于局部线性模型树的高压共轨柴油机排放模型[J]. 车用发动机, 2015(4):16-20. WANG Xin-yu,HE Chao,LI Jia-qiang,et al. Emission model of high-pressure commom rail diesel engine based on local linear model tree[J]. Vehicle Engine, 2015(4): 16-20.(in Chinese)

[16] Kolewe B, Haghani A, Beckmann R, et al. Gaussian mixture regression and local linear network model for data-driven estimation of air mass[J]. Iet Control Theory & Applications, 2015, 9(7):1083-1092.

[17] 逄红. 内燃机神经网络建模与优化控制方法研究[D]. 天津：天津大学, 2003:41-47. FENG Hong. Research on neural network modeling and optimization control method of internal combustion engine[D]. Tianjin: Tianjin University, 2003:41-47.(in Chinese)

[18] Sequenz H. Emission model structures for an implementation on engine control units[C]∥18th IFAC World Congress. Milano,Italy: IFAC , 2011:11851-11856.

[19] Zakharov A, Tikkala V M, Jämsä-Jounela S L. Fault detection and diagnosis approach based on nonlinear parity equations and its application to leakages and blockages in the drying section of a board machine[J]. Journal of Process Control, 2013, 23(9):1380-1393.

[20] 韩恺, 吴滔滔, 赵长禄,等. 基于DOE和神经网络的增压柴油机实时模型建模方法研究[J]. 内燃机工程, 2014,35(1):57-62. HAN Kai, WU Tao-tao, ZHAO Chang-lu, et al. Development of real-time capable turbocharged diesel engine model based on DOE and neural network[J]. Chinese Internal Combustion Engine Enginerring,2014, 35(1):57-62. (in Chinese)

[21] Li Q C, Li D D, Chen Q Y. Prediction of pre-oxidation efficiency of refractory gold concentrate by ozone in ferric sulfate solution using artificial neural networks[J]. Transactions of Nonferrous Metals Society of China,2011,21(2):418-422.

[22] Pan L I, Li F G, Cao J, et al. Constitutive equations of 1060 pure aluminum based on modified double multiple nonlinear regression model[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(4):1079-1095.

[23] 杜巍, 刘福水, 李志杰. 增压柴油机进气压力波动规律的试验研究[J]. 内燃机工程, 2008,29(3):37-40. DU Wei, LIU Fu-shui, LI Zhi-jie. Experimental study on fluctuation of intake pressure in turbocharged diesel engine[J]. Chinese Internal Combustion Engine Engineering, 2008, 29(3):37-40. (in Chinese)

[24] Kimmich F, Schwarte A, Isermann R. Fault detection for modern diesel engines using signal- and process model-based methods[J]. Control Engineering Practice, 2005, 13(2):189-203.

Fault Diagnosis of Intake System of Diesel Engine Based on LOLIMOT

WANG Ying-min1,2， CUI Tao1， ZHANG Fu-jun1， DONG Tian-pu1

(1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081，China;2.College of Water Conservancy and Hydropower, Hebei University of Engineering, Handan 310027, Hebei, China)

Leakage and blocking of intake system of diesel engine may lead to the deterioration of the emissions and fuel economy. An accurate model of intake system is difficult to be established since it is a strong nonlinear system. Thus, a fault diagnosis method based on local linear model tree (LOLIMOT) is proposed for on-line fault diagnosis.The amplitude and phase of intake pressure fluctuation signal and volumetric efficiency are selected as the fault characteristic parameters. LOLIMOT is used to establish the reference models of the parameters. The models are regarded as a function of engine speed and intake density.Three residual signals are generated by using parity equation for calculating their threshold values. The mapping relationship between the residual signal and the fault type is analyzed. Experimental results show that the proposed models give good prediction of fault characteristic parameters, the proposed method can be to diagnose the leakage of engine intake system and the blocking of intercooler.

power machinery engineering; intake system; degradation fault; local linear model tree; fault diagnosis

2016-12-27

武器装备预先研究项目(3030020121104)

王英敏 (1981—) ，女，讲师。E-mail: wymxt@163.com； 张付军(1966—)，男，教授，博士生导师。E-mail: zfj123@bit.edu.cn

崔涛(1981—)，男，讲师，硕士生导师。E-mail: bit_cuitao@sina.com

TK421+.3； TP183

A

1000-1093(2017)08-1457-12

10.3969/j.issn.1000-1093.2017.08.001