多约束条件下战时装备维修任务分配方法

昝翔， 陈春良， 张仕新， 王铮， 刘彦

(装甲兵工程学院 技术保障工程系， 北京 100072)

多约束条件下战时装备维修任务分配方法

昝翔， 陈春良， 张仕新， 王铮， 刘彦

(装甲兵工程学院 技术保障工程系， 北京 100072)

针对现有战时装备维修任务分配中考虑约束条件不足、脱离实际的问题，以指派问题为基础，建立装备维修任务分配模型。该模型是在时间限制和维修能力限制的约束条件下，综合考虑装备修理时间、机动时间和维修能力的变化等因素，以修竣装备的重要度之和最大为目标，进行维修任务分配的最优决策。同时设计一种两阶段启发式算法，运用遗传算法和邻域搜索方法进行模型求解。通过算例和对比分析，验证了该方法的合理性和有效性。

兵器科学与技术； 装备维修任务分配； 多约束； 指派问题； 两阶段启发式算法

0 引言

信息化条件下的战时装备维修任务呈现出数量多、类型复杂、时效性强的特点，因此对装备维修系统提出了更高的要求。战时装备维修任务分配是装备维修决策的重要内容，也是充分发挥战时装备维修系统效能的关键因素之一。

目前，关于装备维修任务分配的研究大多集中在平时维修任务分配，目的是在保证装备可靠性和安全性的前提下减小装备维修费用。例如，Jia等[1]针对新型军械装备维修任务分配和保障资源需求问题，设计了计算机辅助决策系统，提高了维修工作效率。Chen[2]分析了维修任务分配的影响因素，运用区间模糊数解决任务分配过程中的不确定性和模糊性，构建了基于综合平衡的维修任务动态分配模型。凌海风等[3]针对维修任务分配问题，提出多目标粒子群优化算法，以工程装备大修计划为例进行分析。关于战时装备维修任务分配的研究大多集中于维修任务在不同级别维修机构的纵向分配上。例如：Yuan等[4]运用蒙特卡洛仿真构建了维修任务分配模型，解决了战时石油装备维修任务分配问题；陈冰等[5]分析了人才成长率和装备完好率对维修任务分配的影响，研究了维修任务在不同维修级别上的分配方法。随着信息化技术的广泛运用、战场空间的扩展、部队独立作战能力的增强，战术级装备维修需要发挥更加关键的作用。只有在规定时间内完成维修任务才能在作战中发挥作用，同时由于作战时间的缩短，使得战术级往往不可能完成本级别所有的装备维修任务，因此对装备维修任务的合理取舍与划分是发挥战时装备维修作用的关键。本文所述的战时装备维修任务分配指的是战术级战时装备维修任务分配。

通过对战时装备维修任务分配的研究现状分析，发现主要存在以下5个问题：

1)战时维修任务分配研究中，对于维修任务纵向分配的研究较多，对维修任务在某一层次，尤其是战术级上横向分配的研究较少。

2)维修任务分配均以修复最大数量装备或所用时间最短为决策目标，忽略了装备体系中不同类型装备对作战的贡献程度不同，应该增加考虑装备重要度因素，以修复装备的重要度之和最大作为决策目标，才能更好地发挥装备维修对作战的支持作用。

3)没有充分考虑作战时间对装备维修的影响，超过时间限制修复的装备不能对作战做出贡献，对于该次作战属于无效修复。

4)对于战时装备维修，机动巡回维修是装备维修的主要形式，这就要求考虑装备维修单元在不同待修装备损坏位置之间机动的时间因素，这也是装备维修任务分配的重要影响因素。

5)没有考虑装备维修单元能力下降的因素，由于维修资源的消耗和维修人员疲劳累积等原因，装备维修单元的维修能力呈下降趋势，必须充分考虑这一约束条件，才能使得维修任务分配模型更加符合实际。

针对以上问题，本文分析维修时间限制和维修能力限制，考虑装备维修能力下降因素，以最大程度保证装备体系完整性为目标，构建战时装备维修任务分配模型，设计两阶段启发式算法进行求解，并通过算例验证模型的合理性和有效性。

1 基本描述

1.1 概念描述

1)维修任务是装备维修领域的一个常用概念，但是缺乏严格的定义。维修任务在文中的定义为：能够使待修装备恢复到继续参加作战的功能状态所需的全部维修活动的总称，一个维修任务对应一台待修装备。

2)在体系作战的背景下，参战装备需要组成装备体系，发挥整体作战效能。装备重要度指的是装备在装备体系中的重要程度，可以定量地反映装备对作战的贡献。装备重要度越大，对保持装备体系的完整性就越重要。装备重要度可以通过装备在装备体系中的重要度和装备自身重要度两个方面综合评估获得，受到多种因素的影响，会随着装备种类、作战任务等因素的改变发生变化。

3)维修任务分配是指将维修任务划分给装备维修单元。维修任务分配的结果有两个，即每个装备维修单元所需完成的维修任务和完成维修任务的顺序。维修任务分配是静态划分维修任务的过程，即在离散的时间点上对已出现的维修任务进行划分。

4)装备维修单元是战时执行装备维修任务的主体，由维修人员、维修装备和设备以及相关的备品备件组成，具有一定的维修能力、机动能力和防护能力。

1.2 装备维修任务分配描述

装备维修任务分配是在装备保障指挥机构通过信息侦察明确了维修任务相关信息的基础上，以最大程度保持装备体系的完整性为目标，在考虑时间与维修单元维修能力的基础上，对维修任务进行合理划分，明确各维修单元需要完成的维修任务及过程。装备维修任务分配包含以下几个要点。

1.2.1 前提条件

维修任务信息明确，即维修任务数量、工作量、待修装备位置和装备重要度等信息已经确定。

1.2.2 分配目标

装备维修是为作战服务的，以实现对作战的最大支持为目标。为了完成该目标，需要提高修复装备的数量，并且优先修复对作战贡献程度大的装备。由于装备重要度是装备对作战贡献程度的定量反映，综合上述两个方面，装备维修任务分配的目标设定为：修复装备的重要度之和最大。

1.2.3 约束条件

1)时间限制：只有在限定时间内修复的装备才能在本次作战中继续发挥作用，参考相关原则和作战实际，本文设定时间限制为作战时间的2/3，即只有在作战时间的前2/3时间内完成的维修才能对本次作战发挥支持作用。根据战场实际情况，时间因素主要由两个方面组成：待修装备的修复时间和装备维修单元到达待修装备的机动时间。

2)维修能力限制：每个装备维修单元所能承受的维修工作量有一个上限，所分配的工作量不能超过这个上限。考虑完成维修任务需要消耗维修资源并同时产生维修人员的疲劳累积等因素，装备维修单元的维修能力随时间呈下降趋势。

1.3 假设描述

为了简化问题、突出重点，做出如下假设：

1)待分配的维修任务均为本级有能力完成的维修任务。

2)维修任务在分配前已经明确装备重要度、待修装备修理时间以及待修装备位置等信息。

3)忽略装备修理时间的随机性，采用平均修理时间表征装备的修理时间。

4)忽略不同维修专业的影响，只要满足维修工作量要求的待修装备均可以修复。

5)在维修任务分配的过程中，不会出现新的维修任务。

6)只考虑修竣装备对本次作战任务的影响。

7)修复的装备回原单位归建，忽略归建过程中所用的时间，即修复的装备可立即回到原装备体系继续作战。

8)不考虑敌方打击对装备维修单元维修能力的影响和对待修装备的二次伤害。

2 模型建立

指派问题是指在一定约束条件下，将若干任务划分给若干任务主体，如何使得效益最大或消耗最小的问题。文献[6]中提到，该类问题于1955年由Kuhn提出，是整数规划的一个分支。在军事领域，目前被广泛应用于火力打击目标分配[7]、无人机任务分配[8]等问题。非平衡指派问题[9]是指派问题的一种特殊形式，主要用来解决任务与分配主体不平衡条件的指派问题。非平衡指派问题是一个非确定多项式时间可解问题(NP问题)，需要通过遗传算法[10]、蚁群算法[11]、粒子群算法[12]等智能算法及优化方法求解。

装备维修单元需要完成比自身数目多的维修任务，是一个典型非平衡指派问题，可参考非平衡指派问题的相关模型和求解方法解决维修任务分配问题。

2.1 参数定义

为了方便模型的描述，采用如下的参数定义:

1)tmax表示作战持续时间。

2)I为维修任务集合，且|I|=n，n为维修任务的总数。

3)J为装备维修单元集合，且|J|=m，m为维修单元的总数。

4)C为装备重要度的集合，C={c1，c2，…，cn}，c1，c2，…，cn表示各待修装备的重要度。

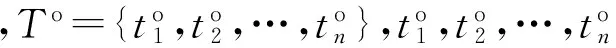
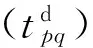
7)T为完成维修任务所需时间的集合，T={t1，t2，…，tn}，t1,t2,…,tn表示修复各待修装备所需的时间。

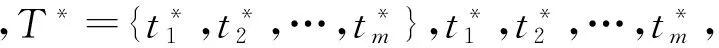
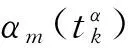
10)xij为分配变量，xij=1表示将第i维修任务分配给第j个装备维修单元，xij=0表示没有将第i维修任务分配给第j个装备维修单元。

2.2 维修任务分配模型

以非平衡指派模型为基础，结合装备维修任务分配特点，可以得到装备维修任务分配模型为

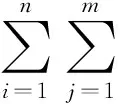
(1)

(2)

(3)

(4)

(5)

xij={0,1}.

(6)

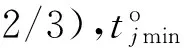
2.3 模型求解

2.3.1 两阶段启发式算法

两阶段启发式算法[13]，是根据需要将问题划分为两个阶段性问题，根据各阶段问题的特点应用不同的启发式算法求解问题的过程。

根据维修任务分配的最终结果，将维修任务分配分解为任务划分和顺序确定两个阶段。第一阶段是通过任务划分，明确维修任务与装备维修单元之间的对应关系，应用遗传算法求解；第二阶段是明确各装备维修单元完成维修任务的先后顺序，由于此阶段可行解较少，为确保搜索的完整性，应用邻域搜索算法[14]进行求解。

2.3.2 算法设计

1)第一阶段——遗传算法

①编码方式：采用整数编码，染色体长度为n，对应维修任务的数量。每个基因在0～m中取整数值，0表示该任务没有被分配，1～m表示任务分配给对于标号的装备维修单元。

②种群初始化：通过随机数产生初始种群，初始种群中每个染色体上的编码都在0～m之间随机取正整数。

③交叉与变异：交叉采用单切点交叉法，通过正比例选择策略选择父代染色体。变异采用交换变异，即选择染色体中的若干个基因交换位置。

2)第二阶段——邻域搜索

①编码方式：采用整数编码，对每个维修单元所分配任务按照编号从小到大的顺序进行编码。

②搜索方法：采用随机变化法实现邻域交换。

③搜索次数：由于每个维修单元所分配任务的数量存在差异，搜索次数会随着维修任务数量增加呈几何倍数增长。设维修单元所示分配维修任务量为Q，设置一个上限值M，搜索次数设定为min (M,Q!).

3)适应度函数

适应度函数为维修任务分配模型的目标函数。

4)编码转化

两阶段涉及的编码不同，需要进行转换，设计如下的转化方式：

①对任意染色体CH，在邻域搜索前用S1～Sm共m个向量提取染色体上m个装备维修单元各自对应的维修任务，然后对S1～Sm分别进行邻域搜索，进行时间约束和维修能力约束的判断，并获得符合条件的最优执行顺序，同时计算对应的装备重要度之和C′1～C′m.

②用向量S作为染色体CH的输出向量获取最优执行顺序，不同装备维修单元对应的执行顺序用数字0隔开，即

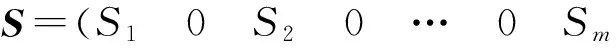
(7)

这样就可以建立CH与S的一一对应关系，易得S的最大长度为n+m-1. 同时对C′1～C′m进行求和，获得该染色体对应的适应度值C′max.

5)约束条件判断

获得备选方案后，首先对约束条件进行判断，若不符合约束条件，则该方案不是可行解，无需进行后续运算步骤。

①时间约束判断：结合(4)式、(5)式、(6)式对时间约束进行判断。

②维修能力约束判断：由于维修能力约束具有实时性，需要在每次随性维修任务前进行判断。若装备维修单元j的备选方案为(j1,j2,…,jq)(1≤q≤n)，即按照j1,j2,…,jq顺序遂行维修任务，则必须满足对∀λ，均有

(8)

则备选方案符合维修能力约束条件。

6)运算步骤

运用两阶段启发式算法求解模型的步骤为：

步骤1 给定初始参数：种群规模K、遗传算法最大迭代次数L、交叉概率Pc、变异概率Pm，邻域搜索上限M.

步骤2 随机产生规模为K的初始种群U0，初始化遗传算法迭代次数l=0.

步骤3 判断截止条件，若l≤L，转到步骤4，否则，转到步骤11.

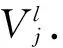
步骤5 对初始编码进行邻域搜索，产生新邻域后进行时间约束和维修能力约束判断，不符合条件的适应度值设为0，符合条件的计算出适应度值。

步骤6 将各染色体最优结果所对应的适应度值作其适应度值，更新此维修任务最优分配结果。

步骤7 从种群Ul中依据正比例选择策略选择父代个体。

步骤8 取ζ∈[0,1]的随机数，若ζ>Pc则将父代个体保留，否则将按照单切点交叉算子得到子代个体，转到步骤9.

步骤9 取ζ∈[0,1]的随机数，若ζ>Pm则个体不发生变异，否则按照变异算子对个体进行变异，得到子代种群，转到步骤10.

步骤10 计算子代染色体的适应值，将子代种群与父代种群合并，用子代个体代替父代中适应值小的个体，计算各个染色体的适应值并按从大到小排序；令l=l+1，保留前K个染色体作为新的种群Ul，返回步骤3.

步骤11 运算终止，输出最优解(包括最优分配结果bestnote和对应的装备重要度之和Cmax)。

3 算例分析

3.1 算例背景

为了验证维修任务分配模型，构建了以下算例：某团执行机动进攻作战任务，该团共有100台装甲装备和15台自行火炮装备等主战装备。经过一段时间后，由于故障和敌方火力打击，装备陆续出现损坏，通过信息侦察，属于本级维修任务的共有18个(编号为1～18)，该团派出3个装备维修单元(编号为1、2、3)遂行装备维修任务。

表1 维修任务基本信息

装备维修任务相互距离信息，即装备维修单元在各装备维修任务之间的机动时间，如表2所示。

维修任务约束条件信息，包括各装备维修单元的初始维修能力(所能承担的初始最大工作时间)信息和作战时间信息，如表3所示。

3.2 维修任务分配结果

根据维修任务分配模型，将算例中的基本信息作为输入条件，通过设计的算法(取K=20，L=50，Pc=0.85，Pm=0.01，M=2 000)，利用MATLAB软件运算，得出迭代结果如图1所示。

计算结果为

表2 维修任务相互距离信息

表3 维修任务约束条件信息

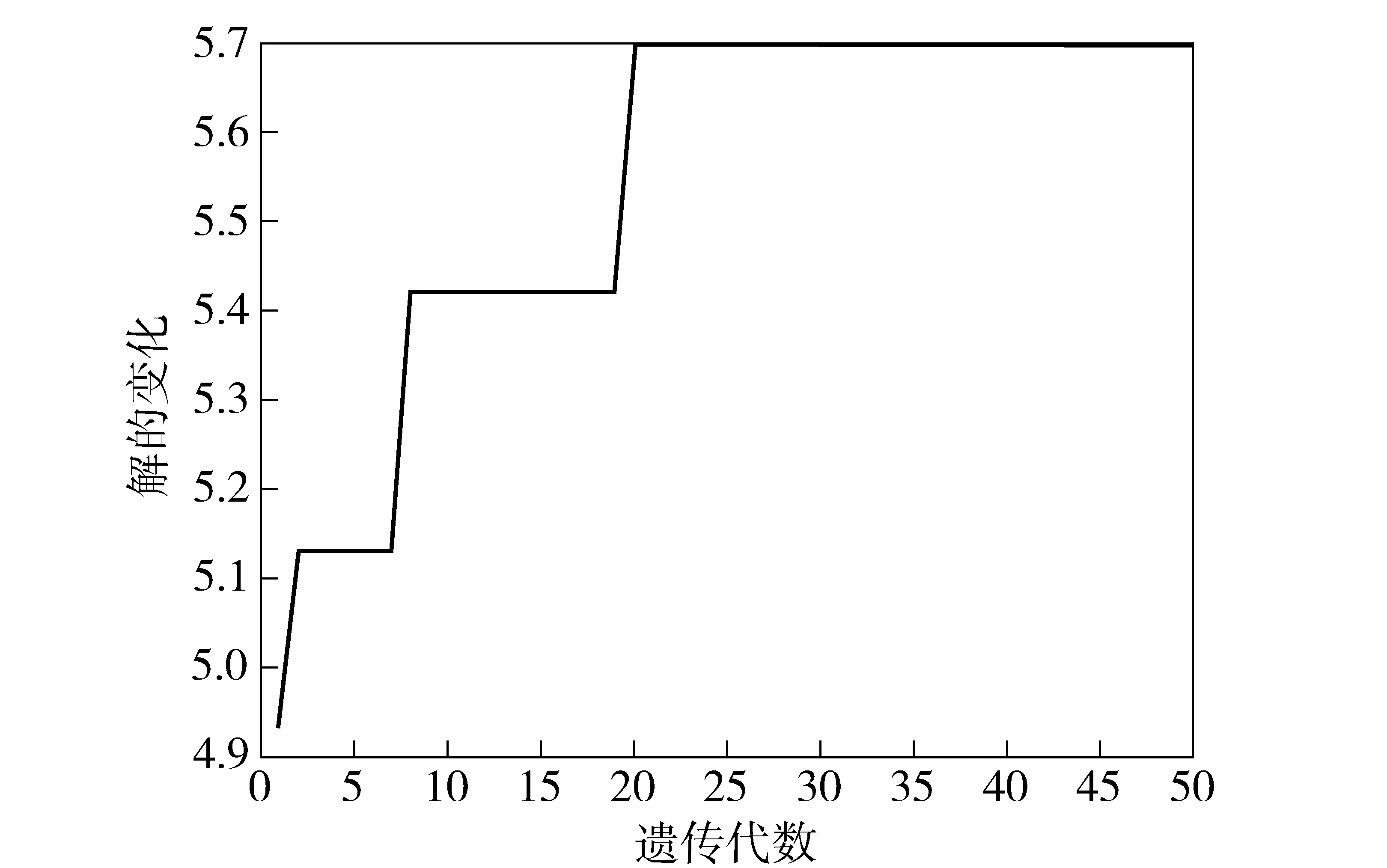
图1 遗传算法迭代结果Fig.1 Iteration result of genetic algorithm

(9)

Cmax=5.697.

(10)

即维修任务分配结果如表4所示。

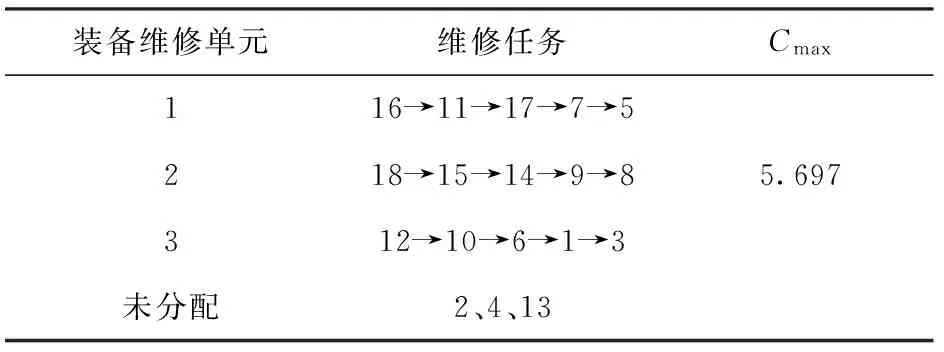
表4 维修任务分配结果

3.3 结果分析

本文主要考虑了维修任务的时间限制和维修能力限制两大约束条件，并且以完成维修任务的装备重要度之和最大为决策目标，在同样的背景下分别释放约束条件，计算最优分配结果如表5所示。

通过表4与表5对比，可得：

1)在不考虑维修能力限制的条件下(表5条件1)，所对应的Cmax为5.915高于表4中的Cmax为5.697，但是分配装备维修单元2的维修任务工作量为165 min，大于其实际维修能力，不符合实际情况，属于无效解。

2)在不考虑时间限制的条件下(表5条件2)，装备维修单元可以完成所有的维修任务，所对应的Cmax也最大。但是，分配给装备维修单元2的维修任务1、维修任务3和分配给装备维修单元3的维修任务17、维修任务18，均是在作战时间的后1/3完成的，不能对作战起支持作用，属于无效修复。而去除无效修复以后，条件2所对应的Cmax下降为5.072，小于表4中的Cmax为5.697.

表5 维修任务分配结果对比

3)在不考虑装备重要度时(表5条件3)，所对应的Cmax为5.119小于表4中的Cmax为5.697.

通过以上分析，可以发现本文所述方法可以获得满足约束条件的最优可行解，可以有效地解决多约束条件下的战时维修任务分配问题。

4 结论

1)维修能力限制是战时装备维修任务分配的重要约束条件，忽略这个条件会出现不可行解，使得装备维修单元可能无法完成所分配的全部维修任务，从而影响装备维修系统效能的充分发挥。

2)时间限制是战时装备维修任务分配的重要约束条件，忽略这个条件可能会出现无效修复，不能充分发挥装备维修对作战的支持作用。

3)将装备重要度作为维修任务分配目标的重要影响因素，以修复装备重要度之和最大作为决策目标，更加能够发挥战时装备维修系统保证装备体系完整的作用。

战时装备维修任务分配需要满足必要的约束条件，才能使维修任务分配更加合理有效，更好地为体系作战服务。

References)

[1] Jia Y X, Sun L, Wang Y B, et al. Research on maintenance task allocation and support resource requirement analysis for ordnance equipment[C]∥2012 International Conference on Quality, Reliability, Risk, Maintenance and Safety Engineering. Chendu, Sichuan, China: IEEE, 2012:459-465.

[2] Chen H G. The dynamic allocation model of equipment maintenance task based on comprehensive balance[C]∥2010 3rd International Conference on Information Management, Innovation Management and Industrial Engineering. Kunming, Yunnan, China: IEEE, 2010,11:3-9-323.

[3] 凌海风,周献中,江勋林,等.基于多目标粒子群优化算法的装备维修任务分配[J].计算机应用研究, 2012,29(6):2090-2092. LING Hai-feng, ZHOU Xian-zhong, JIANG Xun-lin, et al. Study on equipment maintenance task assignment based on multi-objectives particle swarm optimization[J]. Application Research of Computers, 2012,29(6):2090-2092. (in Chinese)

[4] Yuan C, Guo L B, Yong Q D. Research on the maintenance task allocation of oil equipment[C]∥2012 IEEE Symposium on Robotics and Applications. Kuala Lumpur, Malaysia: IEEE, 2012:97-100.

[5] 陈冰,朱小冬,王毅刚,等.装备完好率要求和人才成长规律的维修任务分配方法[J].火力与指挥控制,2014,39(9):96-99. CHEN Bing， ZHU Xiao-dong， WANG Yi-gang, et al. Research on materiel readiness rate and talented person growing law of task allocation model[J]. Fire Control & Command Control,2014,39(9):96-99. (in Chinese)

[6] 申卯兴,曹泽阳,周林.现代军事运筹[M].北京:国防工业出版社,2015. SHEN Mao-xing, CAO Ze-yang, ZHOU Lin. Modern military operations research[M].Beijing: Natonal Defense Industry Press, 2015. (in Chinese)

[7] Zhang Y, Yang R N, Zuo J L, et al. Improved MOEA/D for dynamic weapon-target assignment problem[J]. Journal of Harbin Institute of Technology,2015,22(6):121-128.

[8] Gottlieb Y, Shima T. UAVs task and motion planning in the presence of obstacles and prioritized targets[J]. Sensors, 2015,15(11):29734-29764.

[9] Lampang A, Boonjing V, Chanvarasuth P. A cost and space efficient method for unbalanced assignment problems[C]∥2010 IEEE International Conference on Industrial Engineering and Engineering Management. Macao: IEEE, 2010:985-988.

[10] Jammoussi Y A, Ghribi F S, Masmoudi S D. Genetic algorithms-based dominant feature selection for face detection application[J]. International Journal of Computational Vision and Robotics,2016,6(1): 77-93.

[11] Eftekhari M, Eftekhari M. Controller design for multivariable nonlinear control systems based on gradient-based ant colony optimisation[J]. International Journal of Modelling, Identification and Control, 2016,25(1): 38-47.

[12] Gu F Q, Liu H L, Li X Q. A fast evolutionary algorithm with searching preference[J]. International Journal of Computational Science and Engineering,2016,12(1): 29-37.

[13] Guemri O, Beldjilali B. Two-stage heuristic algorithm for the large-scale capacitated location routing problem[J]. Journal of Guidance Control and Dynamics,2016,39(9): 1934-1948.

[14] Wang P, Reinelt G, Tan Y J. Self-adaptive large neighborhood search algorithm for parallel machine scheduling problems[J]. Journal of Systems Engineering and Electronics,2012,23(2):208-215.

Task Allocation Method for Wartime Equipment Maintenance under Multiple Constraint Conditions

ZAN Xiang, CHEN Chun-liang, ZHANG Shi-xin, WANG Zheng, LIU Yan

(Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

A model of equipment maintenance task allocation is established for lack of constraint conditions of existing wartime equipment maintenance task allocation. The model can be used for optimal decision of maintenance task allocation in the case of time constraint and maintainability limitation. And the equipment repair time, maneuver time and maintainability are comprehensively considered in the model. A two-stage heuristic algorithm, including genetic algorithm and neighborhood searching method, is designed to solve the model. The effectiveness of the proposed algorithm is verified through example analysis and comparison.

ordnance science and technology;equipment maintenance task allocation; multiple constraint; assignment problem; two-stage heuristic algorithm

2017-01-16

军队科研计划项目(2015WG57)

昝翔(1989—)，男，博士研究生。E-mail：994401550@qq.com

陈春良(1963—)，男，教授，博士生导师。E-mail：chenchunliang@163.com

E92

A

1000-1093(2017)08-1603-07

10.3969/j.issn.1000-1093.2017.08.019