考虑测量误差的步进加速退化试验建模与剩余寿命估计
2017-09-03刘小平张立杰沈凯凯高强
刘小平, 张立杰, 沈凯凯, 高强
(1.燕山大学 先进锻压成形技术与科学教育部重点实验室, 河北 秦皇岛 066004;2.燕山大学 河北省重型机械流体动力传输与控制重点实验室, 河北 秦皇岛 066004)
考虑测量误差的步进加速退化试验建模与剩余寿命估计
刘小平1,2, 张立杰1,2, 沈凯凯1,2, 高强1,2
(1.燕山大学 先进锻压成形技术与科学教育部重点实验室, 河北 秦皇岛 066004;2.燕山大学 河北省重型机械流体动力传输与控制重点实验室, 河北 秦皇岛 066004)
步进应力加速退化试验已发展成高可靠、长寿命产品可靠性评估与剩余寿命估计的主要试验方法。为研究测量误差在基于步进应力加速退化试验方法剩余寿命估计中的影响,建立了基于Wiener过程的考虑个体差异和测量误差的退化模型。将Wiener过程的漂移系数随机化描述个体差异,在首达时间意义下得到了寿命分布的概率密度函数。基于极大似然估计法对模型中引入的未知参数进行估计。采用蒙特卡洛方法对激光器的性能退化进行了仿真研究。研究结果表明,考虑测量误差的退化模型的模型拟合性和剩余寿命估计精度都优于不考虑测量误差的方法,可以提高可靠性估计的精度与剩余寿命预测的准确性。
概率论; 随机过程; 剩余寿命估计; 步进应力; 测量误差; 极大似然估计
0 引言
材料性能的提高和制造技术的进步极大地提高了产品寿命和可靠性,诞生了高可靠、长寿命产品。然而高可靠、长寿命产品的可靠性评估与剩余寿命估计成了产品研制和使用中棘手的问题,军工、航空航天及电子工业等多个领域已对高可靠、长寿命产品的可靠性评估与剩余寿命估计提出了高效准确的要求[1-3]。
步进应力加速退化试验(SSADT)使用样本少,可在短时间内获得寿命试验以外的反映产品可靠性的性能退化数据。不仅克服了寿命试验可靠性信息少、信息获取难的缺点,也克服了恒定应力加速退化试验样本量大、低应力下退化速度慢的缺点,成为高可靠、长寿命产品可靠性评估与剩余寿命预测的有效试验方法[4-10]。
在现有加速退化建模方法中,Wiener过程能够体现性能退化在时间轴上的不确定性,并且在首达时间意义下具有良好的统计分析特性,在退化过程建模和剩余寿命估计中得到了广泛的研究[10-17]。在恒定应力下,Peng等[12]对同时考虑测量误差与个体差异的线性Wiener过程的参数估计方法与剩余寿命分布进行了研究;司小胜等[10]在文献[12]的基础上研究了带测量误差的非线性Wiener过程退化建模与剩余寿命估计,同时考虑了退化中的个体差异。
然而,现有文献对基于Wiener过程的步进应力加速退化建模并没有同时考虑个体差异与测量误差对参数估计精度的影响。唐圣金等[15]基于Wiener过程对步进应力加速退化试验进行了建模与剩余寿命估计研究,考虑了个体差异却没有考虑测量误差;肖倩等[17]在步进应力下建立了考虑测量误差的线性Wiener过程退化模型,进行了优化设计,没有对该模型进行统计分析,也没有考虑个体差异。
在剩余寿命估计中,个体差异与测量误差都是普遍存在的。为了在SSADT场合下同时考虑个体差异和测量误差对建模精度的影响,本文将Wiener过程漂移系数随机化来体现个体差异,引入测量误差对观测数据的影响建立了退化模型。针对步进应力下的性能退化特征数据,提出了一种基于极大似然估计法的退化模型未知参数估计方法。最后,通过仿真分析对本文提出的模型进行了验证。
1 退化建模及剩余寿命估计
从前面的分析可见,Wiener过程能够很好地描述退化过程的动态特性和理解产品失效的本质。假设产品真实的性能退化过程能用线性Wiener过程描述,则单个应力下的产品性能退化过程为
x(t)=x(0)+λt+σB(t),
(1)
式中:x(t)为t时刻产品性能退化真实值;x(0)为退化初值,为方便分析,令x(0)=0;λ为漂移系数,表征产品性能退化速度;B(t)为标准布朗运动,表征退化动态特性;σ为扩散系数。
然而,真实的退化数据由于受到仪器或者环境引起的随机误差影响,难以精确测量。类似于文献[10,12]在恒定应力下带测量误差的Wiener过程建模方法,测量值可以描述为
y(t)=x(t)+ε,
(2)
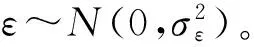
设产品的失效阈值为w,常用真实退化过程的首达时间定义产品寿命T,即
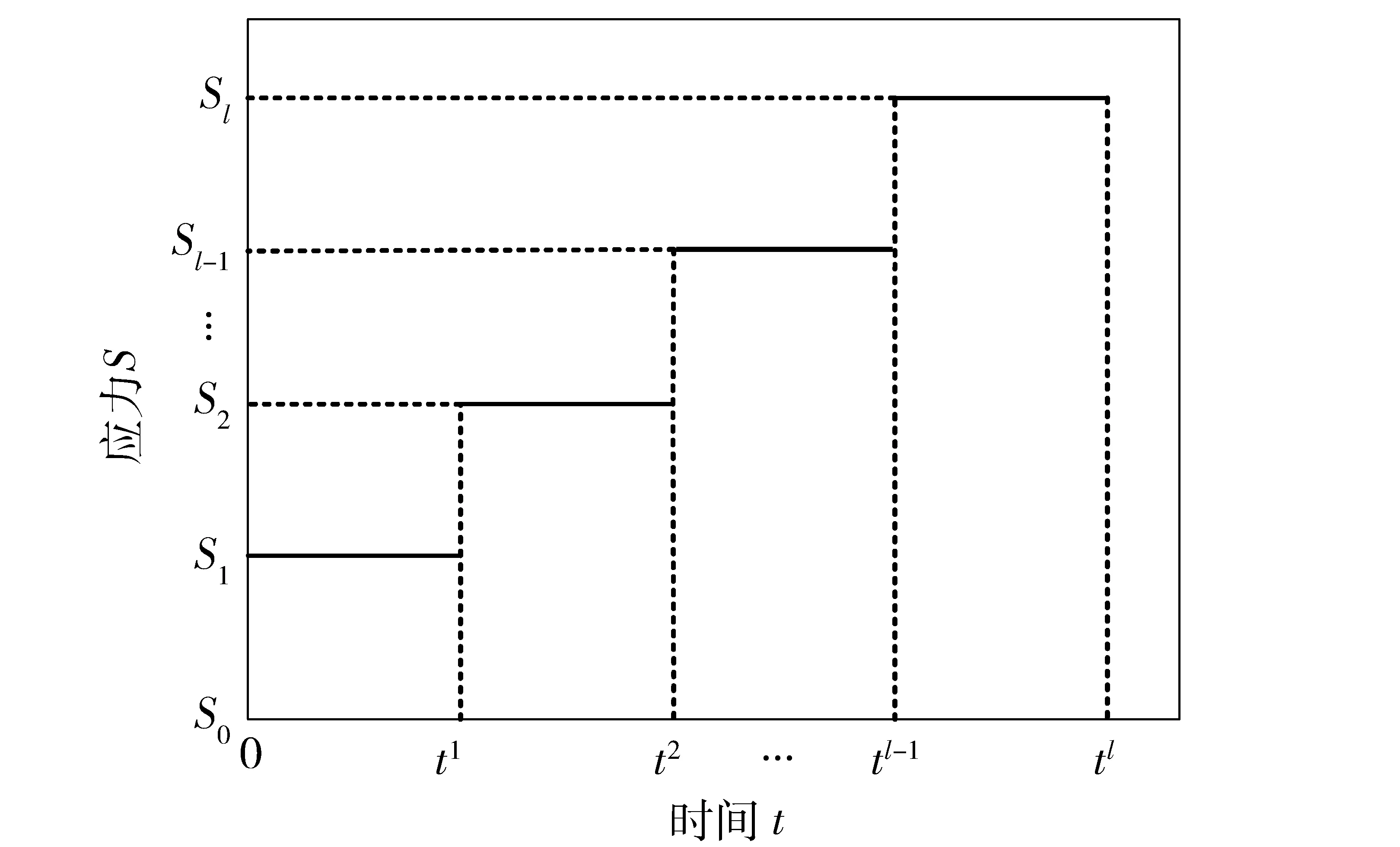
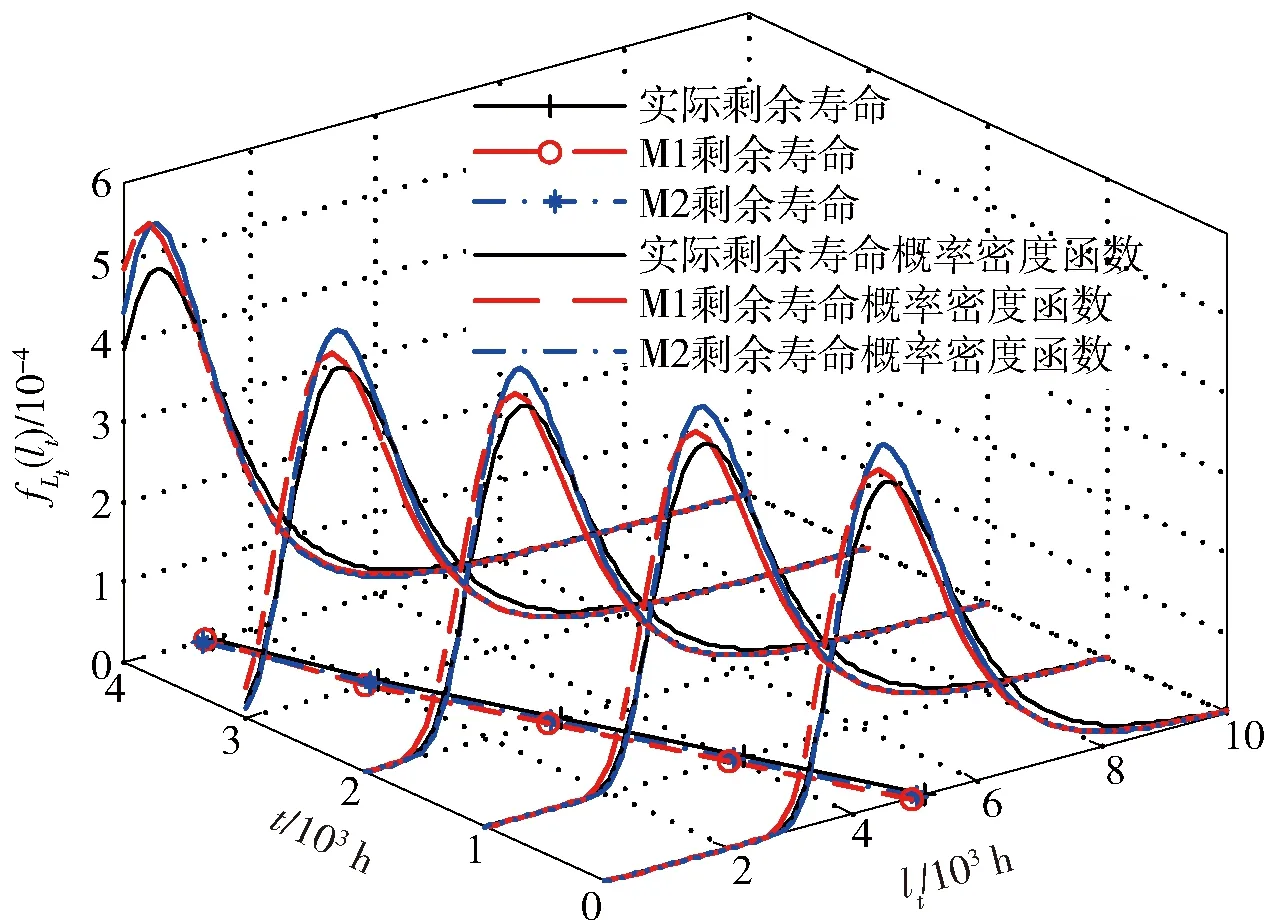
T=inf{t:x(t)≥w|x(0) (3) 当λ为固定参数时,线性漂移Wiener过程的首达时间分布服从逆高斯分布,对应的概率密度函数为 (4) (5) (6) 根据剩余寿命的定义,Lt=inf{lt:T-t|T>t},不难得到t时刻的剩余寿命概率密度函数、可靠度函数以及剩余寿命的期望值分别为 fLt(lt)=f(t+lt)/R(t), (7) (8) (9) 从(6)式和(9)式可以看出,在常应力下,对于可以用Wiener过程描述性能退化的高可靠、长寿命产品,其可靠性评估与剩余寿命估计都可以解析确定,接下来研究如何采用SSADT实现快速的可靠性评估与剩余寿命预测。 加速模型的选择是实现加速退化试验中关键的一步,常见的有阿伦尼斯模型、艾林模型和逆幂律模型[15]。本文以表征温度应力与退化速度之间关系的阿伦尼斯模型为例,给出考虑测量误差的SSADT建模方法以及下节未知参数估计方法,其余加速模型的使用与此模型类似。对基于Wiener过程的SSADT而言,一般认为Wiener过程的漂移系数与应力有关,而扩散系数与应力无关,相应的加速模型为 λ(S)=aexp (-b/S), (10) 假设各步进应力下的失效机理不发生变化,l步步进应力试验加载顺序如图1所示。Si表示第i步加速应力,ti表示完成第i步加速应力的时间。由(10)式加速模型可知,不同加速应力下有不同的退化速度,即漂移系数 λi=λ(Si)=aexp (-b/Si),i=1,2,…,l. (11) (12) 图1 SSADT应力加载顺序Fig.1 SSADT stress loading sequence 本节基于极大似然估计方法对退化模型未知参数进行估计。对于不考虑个体差异的退化过程,只需按照Wiener过程的独立增量性就可以进行参数估计;对于考虑个体差异却不考虑测量误差的退化过程,文献[15]给出了两步极大似然估计方法进行参数识别,文献[12]给出了在常应力下同时考虑个体差异与测量误差的Wiener过程未知参数模型估计方法,本节给出带测量误差的SSADT模型的参数估计方法。 由于条件限制,SSADT更多地适用于内场试验,因此可以假设各试样的测量间隔与测量次数相同。假设共有N个试样进行试验,共有l步步进加速应力,由(12)式可得,第j个样本在应力Si下的第k次测量性能退化观测值为 (13) (14) 各个产品性能退化量测量值之间相互独立,则样本的对数似然函数为 (15) 计算(15)式关于μa和σa的1阶偏导数[12],得到 (16) (17) 令(16)式和(17)式等于0,得到σa和σa的受限极大似然估计值如下: a(σ,σε,b)=, (18) (19) 将(18)式和(19)式代入(15)式中,得到未知参数的剖面对数似然函数如下: (20) 参数σ、σε和b的极大似然估计值可以采用多维搜索算法最大化剖面似然函数(20)式得到,采用Matlab中的fminsearch函数实现,将得到的极大似然估计值、ε和代入(18)式和(19)式,则可以得到a与a. 本节以激光器SSADT蒙特卡洛仿真来验证本文所提方法,计算结果仅用来说明方法的正确性,不对激光器试验构成指导。针对激光器[18]的试验数据,采用文献[12]提出的方法得到参数值λ=2.04×10-3,σλ=4.20×10-4,μa=12.55,σa=2.58,σ=1.04×10-2,σε=3.09×10-2. 激光器的运行性能特征参数对温度应力较敏感,假设产品主要受温度应力的影响,则性能退化速度与温度应力之间的关系符合阿伦尼斯模型。当运行性能特征参数超过失效阈值,则认为其失效,预设失效阈值w=10. 设正常工作温度为25 ℃,令b=2 600,取步进应力分别为25 ℃、50 ℃、75 ℃,分别每隔150h测量一次,每个应力下测量5次,仿真的8个试样步进应力加速退化曲线如图2所示,具体数据见表1. 图2 SSADT退化曲线Fig.2 SSADT degradation curves 将文献[15]提出的不考虑测量误差的步进应力加速退化试验数据处理方法记为M1,本文提出的方法记为M2,引入赤池信息量准则(AIC)和总体均方误差(TMSE)作为评价方法好坏的标准[15]。AIC的值越小,模型拟合的优良性越好,TMSE的值越小,寿命估计的准确性越高,二者计算公式如下: AIC=2(k-lnL(θ)), (21) (22) 分别采用两种方法计算的各参数估计值、AIC、TMSE、平均失效时间(MTTF)和对数似然函数的最大值(Log-LF)如表2所示,TMSE是以时间间隔为1×103h在区间[0,1×104h]内的10个测量点的计算值。 从表2真实值可以看出,原始数据的误差标准差非常小,表明原始数据受测量误差的影响较小,仿真的各个阶段退化曲线(见图2)都接近于直线,也证明了这一点。采用方法M2对仿真数据进行统计分析,结果(见表2)非常地接近真实值,说明了本文方法的正确性。方法M1没有考虑测量误差,测量误差通过表示,导致值偏大。相比方法M1,方法M2的Log-LF值较大,AIC值较小,说明本文方法模型拟合性优于方法M1;方法M2的TMSE值也小于方法M1,MTTF值更接近真实值,说明本文方法具有更好的寿命估计精度。总体来说,方法M2比方法M1在模型拟合性和寿命估计精度两个方面都较优。 表1 SSADT退化数据 表2 方法M1与M2的比较 为了更直观说明方法M2的正确性以及参数估计的准确性,根据(5)式~(9)式,利用表2中的参数估计结果可得图3~图5概率密度函数、可靠度以及剩余寿命概率密度函数。从中不难发现,方法M2的曲线更接近于真实值,表明本文提出方法的准确性。 图3 方法M1与M2的概率密度函数比较Fig.3 Comparison of probability density functions of M1 and M2 图4 方法M1与M2的可靠度函数比较Fig.4 Comparison of reliability functions of M1 and M2 图5 方法M1与M2的剩余寿命分布函数比较Fig.5 Comparison of residual life distribution functions of M1 and M2 1)基于线性Wiener过程研究了考虑测量误差的步进应力加速退化建模和剩余寿命估计问题。引入测量误差对观测数据的影响,将漂移系数随机化表示退化过程中产品的个体差异,建立了线性Wiener过程退化模型。 2)真实的退化过程受测量误差的影响,难以直接得到,针对步进应力加速退化试验的测试数据,提出了一种基于极大似然估计的退化模型未知参数估计方法。 3)仿真实例对比分析表明,本文提出的考虑测量误差的步进应力加速退化建模方法模型拟合性和剩余寿命估计精度都优于不考虑测量误差的方法,可以提高可靠性估计与剩余寿命预测的准确性。 References) [1] 潘骏, 刘红杰, 陈文华, 等. 基于步进加速退化试验的航天电连接器接触可靠性评估[J]. 中国机械工程, 2011, 22(10): 1197-1200. PAN Jun, LIU Hong-jie, CHEN Wen-hua, et al. Contact reliability assessment of aerospace electrical connector based on step-up - stress accelerated degradation testing[J]. China Mechanical Engineering, 2011, 22(10): 1197-1200. (in Chinese) [2] Jun Y, Mingge X U, Zhong W. Research of step-down stress accelerated degradation data assessment method of a certain type of missile tank[J]. Chinese Journal of Aeronautics, 2012, 25(6): 917-924. [3] 陈循, 张春华. 加速试验技术的研究、应用与发展[J]. 机械工程学报, 2009, 45(8): 130-136. CHEN Xun, ZHANG Chun-hua. Research, application and development of accelerated testing[J]. Journal of Mechanical Engineering, 2009, 45(8): 130-136. (in Chinese) [4] 潘骏, 王小云, 陈文华, 等. 基于多元性能参数的加速退化试验方案优化设计研究[J]. 机械工程学报, 2012, 48(2): 30-35. PAN Jun, WANG Xiao-yun, CHEN Wen-hua, et al. Research on optimal design of accelerated degradation test plan based on multiple performance parameters[J]. Journal of Mechanical Engineering, 2012, 48(2): 30-35. (in Chinese) [5] 邓爱民, 陈循, 张春华, 等. 加速退化试验技术综述[J]. 兵工学报, 2007, 28(8): 1002-1007. DENG Ai-min, CHEN Xun, ZHANG Chun-hua, et al. A comprehensive review of accelerated degradation testing[J]. Acta Armamentari, 2007, 28(8): 1002-1007. (in Chinese) [6] NAIR V N. Estimation of reliability in field—performance studies: discussion[J]. Technometrics, 1988, 30(4): 379-383. [7] Cai M, Yang D, Zheng J, et al. Thermal degradation kinetics of LED lamps in step-up-stress and step-down-stress accelerated degradation testing[J]. Applied Thermal Engineering, 2016, 107:918-926. [8] Huang J, GoluboviD S, Koh S, et al. Lumen degradation modeling of white-light LEDs in step stress accelerated degradation test[J]. Reliability Engineering & System Safety, 2016, 154:152-159. [9] Wang H, Wang G, Duan F. Planning of step-stress accelerated degradation test based on the inverse Gaussian process[J]. Reliability Engineering & System Safety, 2016, 154: 97-105. [10] 司小胜, 胡昌华, 周东华. 带测量误差的非线性退化过程建模与剩余寿命估计[J]. 自动化学报, 2013, 39(5): 530-541. SI Xiao-sheng, HU Chang-hua, ZHOU Dong-hua. Nonlinear degradation process modeling and remaining useful life estimation subject to measurement error[J].Acta Automatica Sinica, 2013, 39(5): 530-541. (in Chinese) [11] Wang X, Lin S, Wang S, et al. Remaining useful life prediction based on the Wiener process for an aviation axial piston pump[J]. Chinese Journal of Aeronautics, 2016, 29(3): 779-788. [12] Peng C Y, Tseng S T. Mis-specification analysis of linear degradation models[J]. IEEE Transactions on Reliability, 2009, 58(3):444-455. [13] 潘正强, 周经伦, 孙权. 基于 Wiener 过程的步进应力加速退化建模[J]. 系统工程与电子技术, 2011, 33(4): 963-968. PAN Zheng-qiang, ZHOU Jing-lun, SUN Quan. Step-stress accelerated degradation modeling based on Wiener process[J]. Systems Engineering and Electronics, 2011, 33(4): 963-968. (in Chinese) [14] Hu C H, Lee M Y, Tang J. Optimum step-stress accelerated degradation test for Wiener degradation process under constraints[J]. European Journal of Operational Research, 2015, 241(2): 412-421. [15] 唐圣金, 郭晓松, 周召发, 等. 步进应力加速退化试验的建模与剩余寿命估计[J]. 机械工程学报, 2014, 50(16): 33-40. TANG Sheng-jin, GUO Xiao-song, ZHOU Zhao-fa, et al. Stepstress accelerated degradation process modeling and remaining useful life estimation[J]. Journal of Mechanical Engineering, 2014, 50(16): 33-40.(in Chinese) [16] 蔡忠义, 陈云翔, 张诤敏,等. 非线性步进加速退化数据的可靠性评估方法[J]. 北京航空航天大学学报, 2016, 42(3):576-582. CAI Zhong-yi, CHEN Yun-xiang, ZHANG Zheng-min, et al. Reliability assessment method of nonlinear step-stress accelerated degradation data[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016 ,42 (3) : 576-582. (in Chinese) [17] 肖倩, 郭昊, 答雯, 等. 带测量误差的 Wiener 退化过程最佳试验配置设计[J]. 工业工程与管理, 2013, 18(5): 48-52. XIAO Qian, GUO Hao, DA Wen, et al. Design of an optimal test configuration based on Wiener degradation on process with measurement error[J]. Industrial Engineering and Management, 2013, 18(5): 48-52. (in Chinese) [18] Meeker W Q, Escorbar L A. Statistical methods for reliability data[M].Hoboken, NJ, US: John Wiley & Sons, 1998: 642-643. Step Stress Accelerated Degradation Test Modeling and Remaining Useful Life Estimation in Consideration of Measuring Error LIU Xiao-ping1,2, ZHANG Li-jie1,2, SHEN Kai-kai1,2, GAO Qiang1,2 (1.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of Education of China, Yanshan University, Qinhuangdao 066004, Hebei, China;2.Hebei Key Laboratory of Heavy Machinery Fluid Power Transmission and Control, Yanshan University, Qinhuangdao 066004, Hebei, China) Accelerated degradation test (ADT) has been developed into a main test method, which can be used to estimate the reliability and remaining useful life (RUL) of products with high reliability and long life. In order to study the effect of measurement error on the estimation of RUL in the step stress accelerated degradation test, a degradation process modeling based on Wiener process model considering the measurement error and the individual variation is proposed. The drift coefficient of Wiener process is randomized to describe the individual variation in different equipment, and the probability density function of life distribution is obtained at first hitting time. The maximum likelihood estimation method is used to estimate the unknown parameters introduced in the model. Monte Carlo method is used to simulate the performance degradation of laser. The results show that the fitting of model and the accuracy of RUL estimation in the degradation model considering the measurement error are better than those in the model without considering the measurement error, which can enhance the estimation accuracy of reliability and the prediction accuracy of RUL. probability theory; stochastic process; remaining useful life estimation; step stress; measurement error; maximum likelihood estimation 2016-12-08 刘小平(1989—), 男, 博士研究生。E-mail: liu_xp163@163.com 张力杰(1969—), 男, 教授,博士生导师。E-mail: ljzhang@ysu.edu.cn TB114.37 A 1000-1093(2017)08-1586-07 10.3969/j.issn.1000-1093.2017.08.017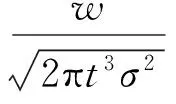
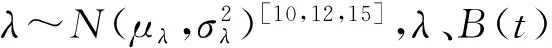
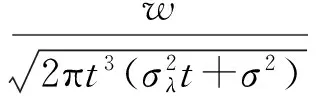



2 步进应力加速退化模型
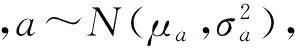


3 参数估计

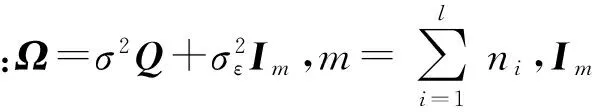



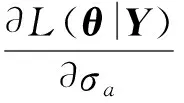


4 仿真分析





5 结论
