固体火箭发动机燃气射流驱动液柱过程中的内弹道研究

王健， 林庆育， 阮文俊， 王浩

(南京理工大学 能源与动力工程学院， 江苏 南京 210094)

固体火箭发动机燃气射流驱动液柱过程中的内弹道研究

王健， 林庆育， 阮文俊， 王浩

(南京理工大学 能源与动力工程学院， 江苏 南京 210094)

为了实现单兵火箭“有限空间内发射”的能力，提出了在尾管内放置液柱平衡体的单兵火箭发射系统，对该系统进行试验研究的同时分时段分析了内弹道过程。以经典内弹道理论为基础，将燃气与液体之间的无规则混合假设为“穿孔混合”，建立了发射系统的数学模型，并运用龙格- 库塔法进行了数值计算，给出了完整的内弹道曲线。通过试验与计算结果的对比分析，计算结果与试验结果吻合较好，燃烧室最大压力相对误差为1.6%，弹丸速度相对误差为0.9%，验证了该模型的有效性，为单兵火箭驱动液柱发射系统的内弹道过程提供理论参考依据。对比分析单兵火箭发射系统在有无液体柱平衡体两种条件下的计算结果可知，在相同发射条件下，液柱平衡体在减弱发射特征的同时提高了弹丸的速度，提升了火箭弹的威力。

兵器科学与技术； 单兵火箭； 液柱； 内弹道； 穿孔混合

0 引言

近年来，在世界各国的武器发展规划中，都着重强调单兵火箭具有“有限空间内发射”的能力，这是因为单兵火箭在发射过程中会伴随着声、光、焰、烟等弊端，为了克服单兵火箭发射过程中存在的固有缺陷，研究发射特征小、能在“有限空间内发射”甚至“封闭空间内发射”的单兵火箭具有重大意义[1]。1977年，前联邦德国研发了“弩”式反坦克火箭筒，该产品首次采用了等质量平衡抛射结构，满足了在有限空间内使用的要求，具有划时代的意义[2]。现今较为先进的单兵火箭武器中，具有火箭燃气消焰性能的有瑞典AT4CS、美国M72E4、德国“铁拳”系列等，其中尤以AT4CS的液体消焰原理的应用较为突出，火箭发射时后喷液体，发射筒后形成水雾，可以有效抑制火箭发射存在的缺陷，并且这种消焰原理已被多数单兵便携式导弹所采用[3]。武瑞清等[4]采用多股环形密集液体工质射流环绕单股燃气射流同轴平行喷射的结构，证明了该燃气消焰的方法是可行的。王珊珊等[5]分析了单兵火箭平衡发射系统内弹道过程，为了方便研究假设平衡体为软性活塞，给出了内弹道曲线和分析计算结果。为了能够有效抑制单兵火箭发射时的燃气射流噪声，张磊等[6]设计了液体水柱放置在尾管中的试验结构，对气体与液体(简称气液)混合物射流噪声声压进行了测量，发现液体水柱起到了显著的降噪效果。

本文在此基础上，采用经典内弹道理论建立了固体火箭发动机燃气射流驱动液柱的计算模型，分析了该单兵火箭发射系统的内弹道过程，并对内弹道过程进行了数值模拟。为了对该模型的有效性进行验证，将计算结果与试验结果进行了对比分析，同时将有无液柱两种状态下的计算结果进行比较，初步分析研究了液体水柱对单兵火箭发射过程中内弹道参数的影响。

1 试验研究

本文研究在尾管内放置液体平衡罐的单兵筒式武器，包括弹丸、燃烧室、液体平衡罐等。具体过程是发射时，击针击发点燃点火药，点火药通过传火机构点燃发射药，发射药燃烧生成大量高温高压气体，在燃烧室形成一定压力。弹底后面的闭气盖和液体消焰罐前面的泡沫堵盖在高压下破碎，液体平衡罐在燃气射流的冲击下破碎吸收火药燃气的能量，从而达到减小火焰、火烟及降噪的目的，其物理模型如图1中所示。

图1 物理模型示意图Fig.1 Schematic diagram of physical model

试验中点火药采用3号小粒黑火药15 g，点火药的装填采用自制点火药盒，点火头采用低电压桥式电发火头，发射药采用双带38共95 g. 模拟弹丸质量为2 kg，液体水罐质量为0.6 kg，炮筒直径为93 mm，弹丸在炮筒内的总行程为435 mm，液体水罐距炮尾距离为215 mm. 试验过程中对燃烧室内的压力进行了测量，测量系统由应变式压力传感器、数据传输线、瞬态记录仪组成。使用网靶对弹丸飞行的平均速度进行了测量，高速摄像仪用来记录发射过程中弹丸和后喷物体的的运动图像，观察液体水柱平衡体的消焰效果。试验现场布置如图2所示。

图2 试验现场布置示意图Fig.2 Schematic diagram of test site layout

图3为单兵火箭弹在有无液柱作为平衡体两种条件下，发射过程中的射流流场分布。从图3中可以看出，在有液柱为平衡体的情况下，射流流场已无后喷火焰高亮区域，说明了液体水罐有明显的消焰效果，减小了发射特征。试验测得有液柱平衡体情况下燃烧室内最大压力为25.05 MPa，弹丸速度为153.3 m/s，满足单兵火箭弹的设计需求。在相同试验条件下，无液柱平衡体的燃烧室内最大压力为14.35 MPa，弹丸速度为127.6 m/s，说明由于液柱平衡体的阻碍作用，使单兵火箭弹在发射过程中燃烧室内的压力升高，对弹丸的推力也变大，在相同发射条件下，弹丸所获初速更高。

图3 有液柱和无液柱情况下的射流流场Fig.3 Jet flow fields with and without liquid column

2 发射系统内弹道模型

2.1 内弹道过程基本假设

带液体平衡罐的单兵火箭内弹道过程包括以下几个过程：点火药被点燃、燃烧室内带状药被引燃、药粒和燃气的流动、燃气在炮筒内膨胀做功、弹丸和液体平衡罐运动等多种物理化学现象。本文采用集总参数法和空间平均的热力学参数来描述火药的燃烧及液体平衡罐的运动，做出以下简化假设：

1)发射药的燃烧基本服从几何燃烧定律和指数燃速定律[7]。

2)发射药在燃烧室内的燃烧和弹丸的运动考虑是在平均压力条件下进行的。

3)在整个发射过程中，燃烧室的燃气成分始终保持不变，与火药性质有关的特征量(火药力、气体常数、绝热指数等)保持不变[8]。

4)热散失、火箭燃气的运动功、摩擦阻力做功等用次要功系数修正。

5)忽略点火过程，假设发射药在一定点火压力下开始燃烧[9]。

图4 穿孔混合假设模型示意图Fig.4 Schematic diagram of hypothesis model of gas-liquid mixing

6)单兵固体火箭燃气射流冲击液柱的过程相当于一个轻微的水下爆炸，气体与液体之间会进行强烈的掺混，并且燃气射流在轴向发展速度高于在径向的发展速度，在液体柱内形成空腔，最终燃气射流与液体在掺混过程中共同流出尾管。由于在试验中观察到炮尾处先出现火光后出现气液流场，因此为了简化模型，假设燃气对液柱的冲击会将其击穿，将燃气与液体的无规则混合假设为“穿孔混合”，即燃气在液体柱中间形成通孔，液体柱变成液体壁管，中间流通燃气。液体壁管在燃气作用下运动，管中间同时有气体流过。在燃气压力作用下，液体管管壁逐渐变薄，燃气通道直径变大，液体管被拉长，假设液体管的体积不变，液体壁管变化过程如图4所示。

7)假设燃气通孔在燃气射流开始冲击液柱的瞬间形成，孔径随着液体壁管的运动逐渐变大，忽略液体的汽化作用。

2.2 内弹道过程时段划分

对于含有液体水柱平衡罐的单兵火箭发射系统，其内弹道过程是十分复杂的，对这个过程进行合理的划分，将有助于建立数学物理模型。根据发射过程中的几个特殊时刻以及试验中所观察到的现象将整个内弹道过程划分为4个时期。

1)第1时期：从点火药开始燃烧到弹和液体水罐同时启动。此时，认为点火药燃完、充满整个高压室、点燃发射药等过程是同时瞬间完成的。这个过程中发射药在燃烧室定容燃烧，生成的燃气使燃烧室压力迅速上升，压力达到设计的启动压力时，弹后闭气盖和液体水罐前的泡沫堵盖破碎，燃气膨胀到弹底和罐底。

2)第2时期：从弹和液体水罐启动到液体全部从炮尾处流出。这一时期是整个内弹道过程中最复杂的一个时段，包括推进剂燃烧、燃气膨胀做功、燃气与液体水的混杂、气液混合物的流动等过程。在该过程中，燃烧室内出现最大压力点，燃气在推动液体水向后运动的同时在液体中穿行，与液体水一起从炮尾处喷出。

3)第3时期：从液体全部流出瞬间到弹底运动到发射筒筒口瞬间。这一时期，燃气继续向前膨胀推动弹丸运动，同时向后从炮尾处喷出。

4)第4时期：从弹底运动到发射筒筒口瞬间到燃烧室压力与大气压力平衡。这一时期，燃烧室及膛内的燃气在发射筒两端喷出，直到与环境大气压力平衡。

2.3 内弹道数学模型

2.3.1 火药燃速方程

燃速定律：

(1)

式中：Z为已燃厚度的百分比；e1为火药初始弧厚的一半；u1为燃速系数；n为燃速指数；p为平均压力；Ze为火药分裂后碎粒全部燃完时的燃去相对厚度。

火药形状函数：

(2)

式中：ψ为火药已燃质量百分比；χ、λ、μ为火药形状特征量。

2.3.2 弹丸和液体罐平衡体运动方程

弹丸运动方程：

(3)

式中：S为炮筒横截面积；m为弹丸质量；v为弹丸速度；l为弹丸行程；φ是虚拟质量系数。

液体罐运动方程：

(4)

式中：ml为弹丸平衡体质量；vl为平衡体速度；ll为平衡体行程。

2.3.3 燃烧室喷孔相对质量流量方程

根据等熵流动的假设，可以给出与液体水混合流出炮筒的燃气相对流量的计算式为

(5)

式中：Sc为燃烧室喷管喉部面积；φ为流量损失系数；τ=T/Tp,T为燃烧室燃气绝对温度，Tp为发射药的爆温；ω为发射药质量；f为发射药火药力；pa为外界环境大气压力；k为绝热指数；ξ为气液混合物中气体的流通比例系数，假设燃气通道面积的变化为液体管行程的正比函数，即

(6)

式中：Ca为液体管全部离开尾管时燃气通道面积与尾管横截面积之比；ll,tot为液体管的总行程；Sa为燃气通过液体柱管通道的横截面积。对于ξ值的确定，首先假设ξ为一变化值，通过数值计算得到燃烧室压力及弹丸速度的变化曲线，与试验所得结果进行对比修正，从而得到ξ的确定值。

2.3.4 能量守恒方程

选取发射筒内的燃气为研究对象，考察燃气系统微过程中的能量平衡。进入系统的能量cvTpωdψ,离开系统的能量cpTωdη+δW,系统储存的能量d[cvTω(ψ-η)],其中：cv和cp分别为燃气定容比热比和定压比热比；δW为燃气系统对外所做的功，可表达为δW=φ1mvdv+φ1mlvldvl，φ1为次要功修正系数。根据热力学第一定律可得：

d[cvTω(ψ-η)]=
cvTpωdψ-cpTωdη-φ1mvdv-φ1mlvldvl.

(7)

(8)

2.3.5 燃烧室燃气的状态方程

药室自由容积为

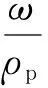
(9)

式中：V0为燃烧室容积；ρp为发射药密度；α为余容；ωB、fB分别为点火药质量和点火药火药力。

状态方程为

(10)

3 数值模拟结果与分析

3.1 数值计算与试验结果对比分析

根据上述物理和数学模型，采用4阶龙格- 库塔法编写了计算程序，并按照单兵固体火箭发动机驱动液柱试验中的装填条件进行了内弹道数值仿真。计算时假设点火药瞬间燃完，作为内弹道方程计算的初始条件[10]。装填参数与结构参数如表1中所示。

表1 内弹道主要装填参数及结构参数

通过数值计算，燃烧室压力随时间的变化规律并与试验结果对比如图5所示。从图5中可以看出，通过数值计算所得燃烧室内压力曲线变化趋势与试验所测得压力曲线吻合较好，试验所得最大压力为25.05 MPa，计算所得最大压力为24.64 MPa，相对误差为1.6%，验证了计算结果的正确性。从燃烧室压力的变化过程可以看出，整个发射过程可以分为3个阶段：第1阶段从点火药燃烧到液柱离开尾喷管瞬间。由于数值计算时假设点火药瞬间燃完，所以计算所得压力在0时刻瞬间上升到8.35 MPa，发射药在此压力下快速燃烧，生成大量的高温高压燃气，同时由于液柱的阻碍作用，燃气大量聚集使燃烧室内压力迅速升高并在液柱离开尾管瞬间达到最大压力点；第2阶段从液柱离开尾管瞬间到弹底离开发射筒瞬间。在该过程中燃气不再受制于液柱的阻碍作用，从尾管中快速喷出，使燃烧室内的压力逐渐下降；第3阶段从弹底离开发射筒瞬间到压力与大气压平衡。在弹底出筒时，燃烧室压力曲线出现拐点，压力下降突然加快，这是由于弹丸从发射筒飞出后，燃气在从尾管喷出的同时在发射筒的前端也快速喷出，使燃烧室内的压力下降加快。

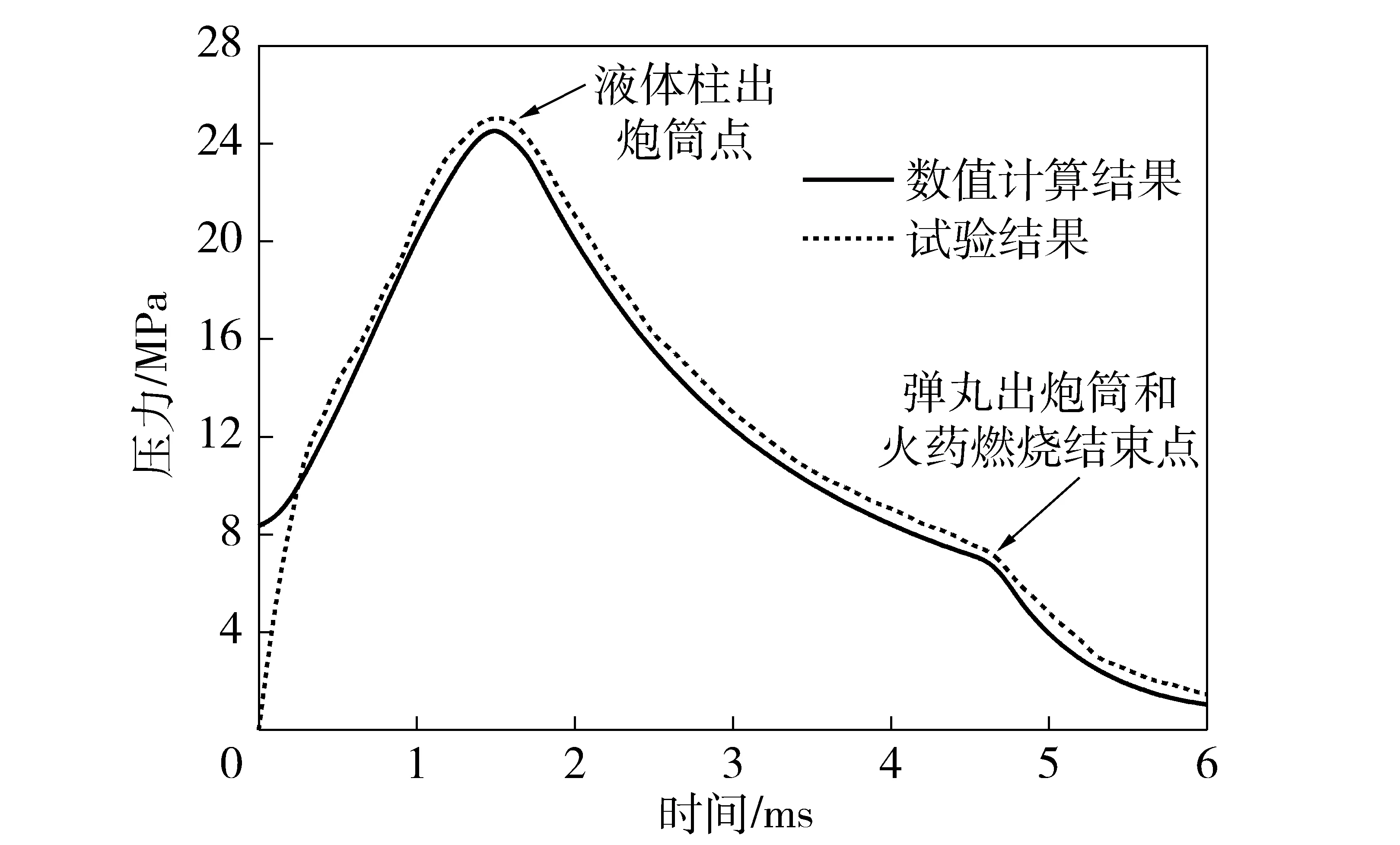
图5 燃烧室压力曲线Fig.5 Curves of pressure in combustion chamber

数值计算所得弹丸速度为151.9 m/s，试验所测弹丸速度为153.3 m/s，相对误差为0.9%. 计算所得速度值略低于试验中实测的弹丸速度值，这是由于数值计算的速度为弹丸底端离开发射筒瞬间的弹丸速度，而试验测得的速度为弹丸从发射筒射出后飞行一段距离后过测速靶线的速度，由于燃气后效期的影响，使得实测弹丸速度略高于计算速度。

3.2 有无液柱情况下计算结果对比分析

为了更准确地了解液柱平衡体对单兵火箭弹发射过程中的影响，在相同的装填参数和结构参数情况下计算得到有无液体柱平衡体两种条件下燃烧室压力、弹丸推力以及弹丸速度曲线，如图6～图8所示，计算结果如表2所示。

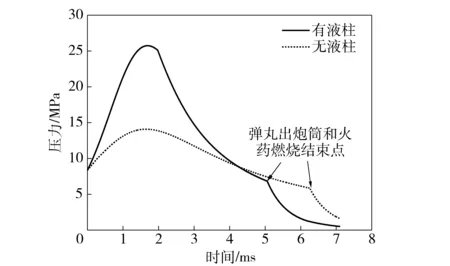
图6 有液柱和无液柱情况下燃烧室压力曲线Fig.6 Curves of pressure in combustion chamber with and without water column

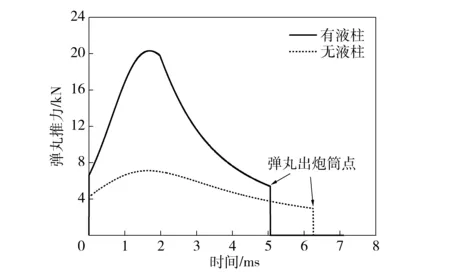
图7 弹丸推力曲线Fig.7 The thrust curves of projectile

有无液柱燃烧室压力峰值/MPa弹丸推力峰值/N弹丸速度峰值/(m·s-1)有液柱24.6420309.2151.9无液柱14.057110.9124.9

从图6可以看出，在无液柱平衡体情况下，单兵火箭弹发射过程中燃烧室内的压力上升及下降均较为缓慢，压力峰值变小，这是由于没有液柱在尾管的阻碍作用，发射药燃烧产生的燃气大部分从尾管喷出，当燃气的产生量小于尾管的流出量后，燃烧室内的压力开始逐渐下降。从图7可以看出，两种情况下弹丸推力曲线的变化趋势与燃烧室压力曲线变化趋势相似，但由于只计算了在炮筒内燃气对弹丸的推力，所以当弹底离开炮筒的瞬间，推力瞬间降为0，弹丸速度也在此刻上升为最大值。从图8可以看出，弹丸在内弹道过程的开始阶段加速较快，当燃烧室压力及弹丸推力达到最大点之后，弹丸的加速逐渐减缓。

对比表2中的计算结果可知，当有液柱平衡体时，燃烧室压力峰值、弹丸推力峰值、弹丸速度峰值均增大，弹丸速度相对增加了21.6%. 计算结果表明，在相同发射条件下，液柱平衡体不仅能减弱单兵火箭弹发射过程中的固有缺陷，还有助于提高弹丸的初速，提升火箭弹威力。

4 结论

本文对单兵火箭驱动液柱发射系统进行了试验研究，并通过编制程序完成了发射过程的内弹道计算。通过试验与计算结果的对比分析，得到如下结论：

1)在单兵火箭发射尾管中加入液柱平衡系统，可以有效地消除发射过程中产生的后喷火焰，减小发射特征，实现“有效空间发射”能力。

2)以经典内弹道理论为基础，提出将燃气与液体之间的无规则混合假设为“穿孔混合”的模型，以此得到的计算结果与试验结果吻合较好，燃烧室最大压力相对误差为1.6%，弹丸速度相对误差为0.9%，验证了该模型的有效性，为单兵火箭驱动液柱发射系统的内弹道过程提供了理论参考依据。

3)通过对比分析有液柱、无液柱平衡系统两种条件下的内弹道计算结果可知，在相同发射条件下，有液柱平衡系统发射过程中的燃烧室压力峰值、弹丸推力峰值、弹丸速度峰值均增大，弹丸速度峰值相对增加了21.6%. 液柱平衡体在减弱发射特征的同时提高了弹丸的速度，提升了火箭弹的威力。

References)

[1] 隋高山.单兵火箭新型发射原理初步探究[D].南京：南京理工大学，2009. SUI Gao-shan. Preliminary study on individual rocket propulsion[D]. Nanjing: Nanjing University of Science and Technology, 2009.(in Chinese)

[2] Kandula M, Lonergan M J. Effective jet properties for the estimation of turbulent mixing noise reduction by water injection[J].AIAA/CEAS Aeroacoustics Conference, 2007, 32(1):253-278.

[3] Thomas D N. Reductions in multi-component jet noise by water injection[R]. Manchester, GREAT BRITAIN:AIAA, 2004:2004-2976.

[4] 武瑞清，阮文俊，李昕，等. 单兵火箭燃气消焰设计的试验研究与数值模拟[J]. 弹箭与制导学报，2009，29(3)：153-157. WU Rui-qing, RUAN Wen-jun, LI Xin, et al. The experimental research and numerical simulation of flame damper design of shoulder launched rocket[J].Journal of Prohectiles,Rockets,Missiles and Guidance, 2009, 29(3):153-157.(in Chinese)

[5] 王珊珊，王浩，阮文俊，等. 单兵火箭平衡发射系统内弹道数值模拟[J]. 南京理工大学学报，2011，35(3)：343-346. WANG Shan-shan, WANG Hao, RUAN Wen-jun,et al. Numerical simulation on interior ballistic of individual rocket balance launching system[J].Journal of Nanjing University of Science and Technology,2011,35(3)：343-346.(in Chinese)

[6] 张磊，阮文俊，王浩，等. 火箭发动机燃气射流驱动液柱降噪实验[J]. 航空动力学报，2016，31(5)：1275-1280. ZHANG Lei, RUAN Wen-jun, WANG Hao, et al. Experiment on jet noise reducing with a liquid column driven by rocket engine gas jet[J]. Journal of Aerospace Power,2016,31(5)：1275-1280.(in Chinese)

[7] 翁春生，王浩. 计算内弹道学[M]. 北京：国防工业出版社，2006:2-16. WENG Chun-sheng,WANG Hao. Computational intetior ballistics[M].Beijing:National Defense Industy Press,2006:2-16.(in Chinese)

[8] 吴蜀豫，吴晓中，王新平. 某小型固体火箭发动机内弹道数值仿真探究[J].电子测试，2014(2)：9-11. WU Shu-yu, WU Xiao-zhong, WANG Xin-ping. Research of interior ballistics numerical simulation for a small solid rocket engine[J].Electronic Test,2014(2)：9-11.(in Chinese)

[9] 严欧鹏. 大推力速燃单兵火箭发动机关键技术研究[D].长沙：国防科学技术大学，2012. YAN Ou-peng.The key technology research of the high-thrust and short-duration individual rocket engine[D]. Changsha:National University of Defense Technology,2012.(in Chinese)

[10] 陈军.固体火箭发动机零维两相内弹道研究[J].弹道学报，2013,25(2)：39-43. CHEN Jun. Research on zero-dimensional two-phase internal ballistics of SRM[J].Journal of Ballistics,2013,25(2)：39-43.(in Chinese)

Study of Interior Ballistics of Solid Rocket Motor in the Process of Gas Jet Driving Liquid Column

WANG Jian， LIN Qing-yu， RUAN Wen-jun， WANG Hao

(School of Energy and Power Engineering， Nanjing University of Science and Technology， Nanjing 210094， Jiangsu, China)

In order to achieve the launch of individual rocket in limited space, a individual rocket launching system of which the liquid column is placed in the tail tube as a balance body is proposed. The system is tested, and the interior ballistics process is analyzed over time intervals. Based on the theory of the classical inrerior ballistics theory, a mathematical model of the launching system is established by assumoffing that the irregular mixing of gas and liquid is regarded as mixing of perforation. Runge Kutta method is used for numerical calculation, and the complete curves of interior ballistics process are given. The analysis result shows that the theoretical results are in good agreement with the experimental results. The relative error of the maximum pressure in combustion chamber is 1.6%, and the relative error of projectile velocity is 0.9%. The calculated results shows that the liquid column can be used to reduce the launching characteristics of rocket, improve the velocity of projectile, and enhance the power of individual rocket for the individual rocket launching systems with and without liquid column under the same launching conditions.

ordnance science and technology; individual rocket; the liquid column; interior ballistic; mixing of perforation

2016-12-19

王健(1990—)，男，博士研究生。E-mail:1805322964@qq.com

阮文俊(1964—)，男，研究员。E-mail:ruanwj@njust.edu.cn

TJ012.1+5； TJ711+.1

A

1000-1093(2017)08-1506-07

10.3969/j.issn.1000-1093.2017.08.007