2017年全国新课标Ⅰ卷理科压轴题的解法分析

广东省惠州市第一中学高中部 李晓波 (邮编:516007)

广东省惠州市博罗中学高中部 易 敏 (邮编:516100)

2017年全国新课标Ⅰ卷理科压轴题的解法分析

广东省惠州市第一中学高中部 李晓波 (邮编:516007)

广东省惠州市博罗中学高中部 易 敏 (邮编:516100)

2017年的高考已落下帷幕,今年的全国新课标卷1理科压轴题简明而清新,突出考查学生的分类讨论与数形结合思想及数学思维的严谨性,要求学生有较好的处理函数与导数问题的基本功和综合能力,它承载着选拔的功能,但并不是让学生感到“不可一试”,笔者按自己的解答撰文评析,供读者参考.

题目 (2017年全国新课标卷Ⅰ理科21题)

已知函数fx()＝ae2x＋(a－2)ex－x.

(1)讨论fx()的单调性;

(2)若fx()有两个零点,求a的取值范围.为了方便,我们只讨论第二问.

解法1 (“站在第一问的肩膀上”)

(i)当a≤0时,由(1)知,fx()在－∞,＋∞(

)上递减,fx()最多有一个零点.(ii)当a＞0,由(1)知,fx()的最小值＋lna.又由于(或f(－2)＞0),＝＋∞(或＞0),因此要使f(x)有两个零点,则必须＋lna＜0,而g′(a)＝0,则g(a)在(0,＋∞)单调递增,且g(1)＝0.于是0＜a＜1时,g(a)＜0.即a∈(0,1),f(x)有两个零点.

评注 此解法较好地利用了第一问的结论,由(1)可知若fx()有两个零点,则必须使fx()的最小值小于0,然后把a的范围解出来,并说明在最小值点的左右两边各取到一个零点即可(或者用极限方法说明).这应该是最多考生采用的方法,比较简洁.

解法2 (“参变分离”)

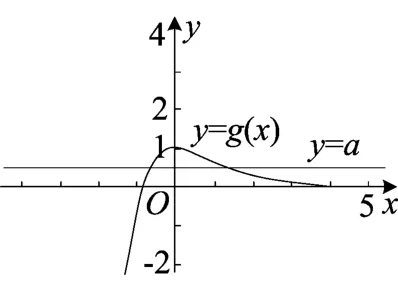
图1

评注 这种解法实质是进行参变分离,f(x)有两个零点,转化为y＝a与的图象有两个交点,从而研

究函数y＝g(x)的图象,再结合图象求出a的范围.这种方法的优点是思路明确,y＝a这个函数比较简单,缺点是函数的求导

等运算比较复杂,在确定它的单调性后,还需要用极限思想(可能需要结合洛必达法则)去判断并准确地画出函数的图象.

解法3 (转化为“一直一曲”)

令t＝ex,由f(x)＝0得g(t)＝at2＋(a－2)t－lnt,t＞0.

f(x)有两个零点即转化为g(t)有两个零点.由g(t)＝0得

(i)当a≤0时,h(t)＝a(t＋1)＜0,此时y＝h(t)与y＝k(t)只有一个交点.

(ii)当a≥1时,h(t)＝a(t＋1)≥t＋1.

所以F(t)在(0,1)递减,在(0,1)递增,因此F(t)的最小值为F(1)＝0,即,当且仅当t＝1时取等号.

所以y＝h(t)与y＝k(t)最多只有一个交点.

(iii)当0＜a＜1时,h(1)＜k(1),当t→0＋时,当t→＋∞时

所以y＝h(t)与y＝k(t)有两个交点.

综上所述,当0＜a＜1时f(x)有两个零点.

评注 此方法与解法二的类似之处就是转化为两个函数的交点问题,是典型的转化为“一曲一直”,虽然过程比解法二复杂一些,但是,它也是一种典型的转化方法.

解法4 (转化为“两曲”)

令t＝ex,方程变形为g(t)＝at2＋(a－2)t－lnt,t＞0,g(t)有两个零点转化成曲线h(t)＝at2＋(a－2)t与F(t)＝lnt有两个交点.(i)当a＜0时,令h(t)＝0得t＝0(舍去),

1＜0(舍去),此时h(t),F(t)最多只有一个交点,不符题意,如图2.

(ii)当a＝0时,h(t)＝－2t,此时h(t), F(t)只有一个交点,不符题意.

(iii)当a＞0时,y＝h(t)的开口向上, h(t)＝0有解t1＝0(舍去),

图2

故g(t)≥0.此时g(t)不可能有两个零点,如图3.

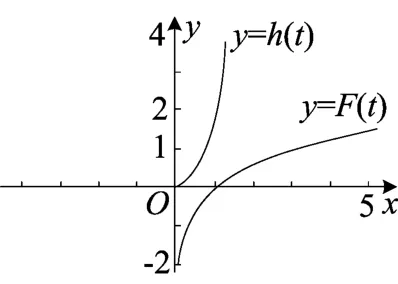
图3

图4

此时h(t)与g(t)有两个交点,符合题意.综上所述,当0＜a＜1时,f(x)有两个零点,如图4.

评注 本法转化为一个二次函数和一个对数函数,虽然两个都是曲线,但是这两个函数都是学生熟悉的典型函数,再加上一点数形结合的思想,不难解决.

事实上,如果我们再大胆地开拓我们的思维,还可以转化为如下两个函数问题.

解法5 (转化为“一凹一凸”)

(i)当a≤0时,g′(x)＝aex≤0,所以g(x)在R上单调递减且恒小于0.y＝g(x)与y＝h(x)不可能有两个交点.

图5

(ii)当a≥1时, g(x)＝aex＋a≥ex＋1.

下面证明ex＋1≥2

(iii)当0＜a＜1时,可知,g(0)＜h(0),且g(－2)＞h(－2),当x→＋∞时,显然g(x)＞h(x),所以y＝g(x)与y＝h(x)有两个交点,如图6.

综上所述,当0＜a＜1时,f(x)有两个零点.

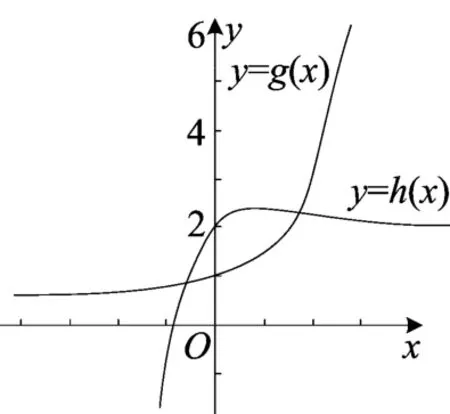
图6

2017-06-29)