挖掘例习题 欣赏圆锥曲线和谐统一之美

甘肃省兰州市第七中学 秦建华 (邮编:611731)

挖掘例习题 欣赏圆锥曲线和谐统一之美

甘肃省兰州市第七中学 秦建华 (邮编:611731)

对人教A版《普通高中课程标准实验教科书·数学》选修1－1圆锥曲线例习题深度的研究.以三角形为载体,几何画板为媒介,深入地挖掘教材中的例习题,欣赏圆锥曲线的和谐统一之美.

圆锥曲线;和谐统一;例习题;几何画板

1 看三角形两边和差等于定常数

椭圆和双曲线有人曾称他们是一对“情侣曲线”,他们的标准方程只差一个运算符号,一个是“＋”,而另一个是“－”,巧合的是在定义里面椭圆说的是到定点距离之和等于定常数,双曲线定义说的是到定点的距离之差等于定常数.图象的对称性完全一致.笔者在椭圆和双曲线的教学过程中,经常用几何画板来展示它们定义的和谐统一和相互转化,使人赏心悦目,从而激发学生对圆锥曲线学习的兴趣.人教A版《普通高中课程标准实验教科书·数学》选修1－1第54页A组第5题.当定点A在圆内就可得命题1,定点A在圆外就可得命题2.

命题1 已知△ABC,顶点A(－c,0),B(c, 0),且CB ＋CA ＝2a(2a＞2c＞0),动点C的轨迹为椭圆,方程

命题2 已知△ABC,顶点A(－c,0),B(c, 0),且动点C的轨迹为双曲线,方程为b＞0).

命题1,2证明从略.

2 看三角形两边之比等于定常数

人教版《全日制普通高级中学教科书·数学》选修第二册上第86页例5推广可以发现.

命题3 已知△ABC,顶点A(－c,0),B(c, 0)(c＞0),且),动点C的轨迹(1)当λ＝1时,轨迹为直线,方程为x＝0; (2)当λ≠1时,轨迹为圆,方程为以为圆心,半径为的圆.

命题3证明从略.

这个圆是著名的阿婆罗尼奥斯圆,简称阿氏圆(ApolloniusofPerga,约前262～约前190,希腊数学家,与欧几里得、阿基米德齐名,他的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地,《圆锥曲线论》是一部经典巨著,它可以说是代表了希腊几何的最高水平,自此以后,希腊几何便没有实质性的进步,直到17世纪的B.帕斯卡和R.笛卡儿才有新的突破).

3 看三角形两边之积等于定常数

对于三角形两边有了和、差、商,我们不难想到三角形两边的积,于是带着好奇进一步探究得出:

命题4 已知△ABC,顶点A(－c,0),B(c, 0),且CB·CA ＝a2,动点C的轨迹方程为[(x＋c)2＋y2][(x－c)2＋y2]＝a4,这是著名的卡西尼卵形线.(乔凡尼·多美尼科·卡西从尼意大利文GiovanniDomenicoCassini,1625年6月8日－1712年9月14日,是一位在意大利出生的法国籍天文学家和水利工程师,曾经工作的单位有旁扎诺天文台,博洛尼亚大学天文学教授,并在1671年巴黎天文台落成后成为该台的第一任总监直到去世.)

4 看三角形两边所在直线的斜率之积等于定常数

人教A版《普通高中课程标准实验教科书·数学》选修1－1第48页探究试题,与例3比较你能发现什么?引起了笔者的思考,对这两道例题的研究发现,斜率的积为正数时,动点M的轨迹为双曲线,斜率的积为负数时,动点M的轨迹为圆或椭圆.椭圆和双曲线有外在的美,也有丰富的内涵,从而有一种和谐统一的方式浮现在眼前,笔者对两个特殊例题深度的研究发现:

命题5 已知△ABC,顶点A(－a,0),B(a, 0),直线CB、CA的斜率分别为k1,k2,k1k2,动点C的轨迹为

(1)当a＝b时,①k1k2＝1(a＝b),轨迹为双曲线,方程为1(x≠±a),等轴双曲线;②k1k2＝－1(a＝b),轨迹为圆,方程为x2＋y2＝a2(x≠±a).

5 看三角形外心

命题6如图已知△ABC,A(a,0),顶点B、C在圆x2＋y2＝r2上同步运动,点P是△ABC的外心,动点P的轨迹是什么?[1]

解 设P(x,y), B(rcosθ,rsinθ),C(rcos(θ＋α),rsin(θ＋α))(其中θ∈(0,2π),α非零实常数).注意到直线AB的垂直平分线方程是

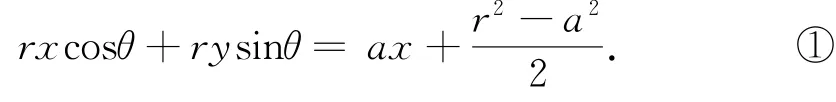
直线AC的垂直平分线方程是rxcos(θ＋α)＋

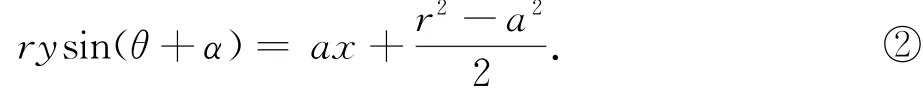
由①②知cosθ＝

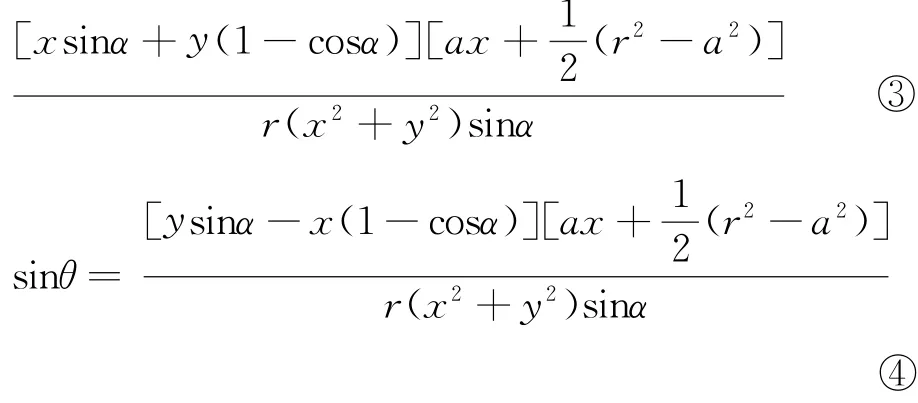
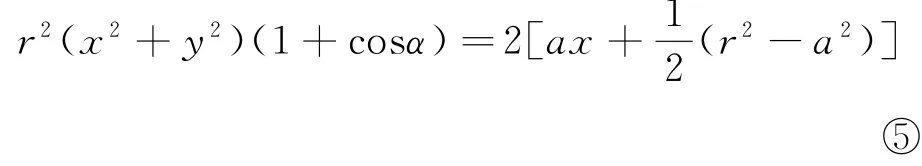
(其中(x2＋y2)sinα≠0,a≠r),由③④知整理⑤得[2a2－r2(1＋cosα)]x2－r2(1＋

这就是圆锥曲线的方程.

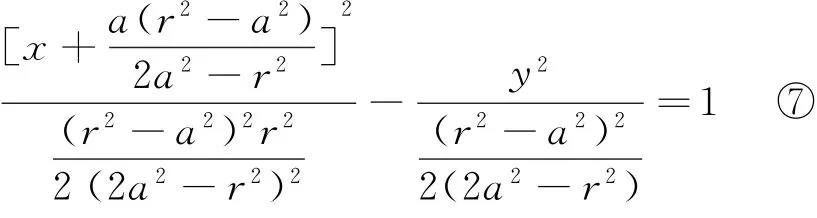
6 教学感悟

敢问新课改的路在何方?路就在脚下.这就需要加强教师自身专业素养,提升教师自身数学研究活动,要站在教材系统的高度教数学,理解数学.以课本为素材进行深度的研究,有助于教师深入认识和理解数学思维,从而使数学课堂教学高效.要求教师注重数学知识的内在联系,关注数学规律的形成过程,就像文中一个普通的三角形,固定两个顶点,另外一个顶点在一定的约束条件下动起来,可以生成圆、圆锥曲线,而且能使他们和谐相处,真的多么美妙!在此还要一提的是用好“几何画板”这个工具,它可以帮助学生探究数学,也可以培养学生的动态思维.

2017-05-17)