有趣的“折线型”函数

江苏省海门中学 杨智慧 (邮编:226100)

有趣的“折线型”函数

江苏省海门中学 杨智慧 (邮编:226100)

含绝对值函数y＝x－a 的图象是“v”型折线,稍复杂一点的是y＝x－a ＋x－b (a≠b)是槽型折线;y＝x－ax－b 则是“z”型折线,我们把这一类形如“y”的函数姑且称为折线型函数.笔者作了一些初步的探究,把发现的性质整理出来,以期抛砖引玉.

考虑一般情况,函数y＝k1·x－a1＋k2· x－a2＋…＋kn·x－an(其中k1,k2,…, kn为非零实数,a1＜a2＜…＜an),应为分布在(－∞,a1),(a1,a2),…,(an,＋∞)这n＋1个区间上的折线段,n个折点分别当x取a1,a2,…,an,时取得.考察函数在这n＋1个区间上线段的斜率:在区间(－∞,a1)上,函数可化为y＝－k1·(x－a1)－k2·(x－a2)－…－kn·(x－an),易得斜率为;在区间(a1,a2)上,函数可化为y＝k1·(x－a1)－k2· (x－a2)－…－kn·(x－an),易得斜率为k1－;在区间(a2,a3)上,函数可化为y＝k1· (x－a1)＋k2·(x－a2)－k3·(x－a3)－…－kn·(x－an),易得斜率为在区间(an,＋∞)上,函数可化为y＝k1· (x－a1)＋k2·(x－a2)＋…＋kn·(x－an)易得斜率为

综上可得如下结论:

性质 函数y＝k1·x－a1＋k2·

x－a2＋…＋kn·x－an(其中k1,k2,…, kn为非零实数,a1＜a2＜…＜an)图象应为分布在(－∞,a1),(a1,a2),…,(an,＋∞)这n＋1个区间上的折线段,n个折点分别当x取a1、a2、…、an,时取得.在区间(－∞,a1)上,线段斜

根据以上性质,我们不难获得如下结论:

推论1 若ki为参数,随着ki的变化,图象上对应折点(ai,yi)是定点,而当ki增大时,折点(ai,yi)左侧部份的图象折线段斜率减少,右侧部份的图象折线段的斜率增大,图象上除定点(ai,yi)外,所有的点均不同程度向上移动.

推论2 函数y＝k1·x－a1＋k2· x－a2＋…＋kn·x－an＋kx－a (其中k1、k2、…、kn、k为非零实数,a1＜a2＜…＜an),a为参数,当a在某个区间(at,at＋1)内变化时,函数图象在所有区间上的折线段斜率不变;当a从某个区间(at－1,at)进入相邻区间(at,at＋1)时,函数图象在at－1左侧所有区间和at＋1右侧所有区间上的折线段斜率不变.

推论3 函数y＝k1·x－a1＋k2· x－a2＋…＋kn·x－an(其中k1,k2,…, kn为非零实数,a1＜a2＜…＜an)在区间(－∞,a1)和(an,＋∞)上的斜率互为相反数,当＞0时,函数整体开口向上,函数有最小值;当＜0时,函数整体开口向下,函数有最大值;当＝0时,函数在区间(－∞,a1)和(an,＋∞)上为两条与x轴平行的射线,有最小值和最大值;

推论4 函数y＝k1·x－a1＋k2·

x－a2＋…＋kn·x－an(a1＜a2＜…＜an),其中k1、k2、…、kn为正实数时,函数在区间(－∞,a1)、(a1,a2)、…、(an,＋∞)上的斜率依次记为K0、K1、K2、…、Kn,则有K0＜0,Kn＞0,且K0＜K1＜…＜Kn,函数的最小值在折线段斜率绝对值Ki的最小值处,Ki为正时,线段左端点取得;Ki为负时,线段右端点取得.

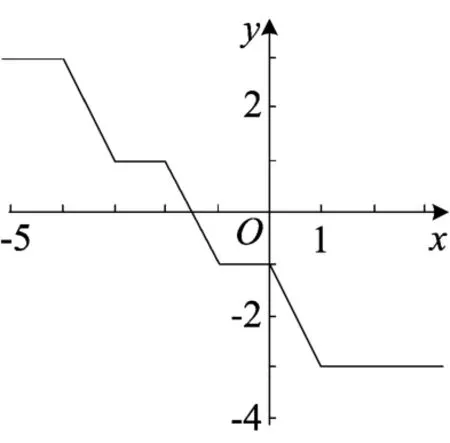
图1

由以上性质及推论我们可以构造一些有趣的折线:如取k1＝－1、k2＝1、k3＝－1、k4＝1、k5＝－1、k6＝1,则折线段的斜率从左至右依次0、－2、0、－2、0、－2、0,可得到阶梯形的函数(如图1)y＝－x＋4＋x＋3－x＋2＋x＋1－x＋x－1;

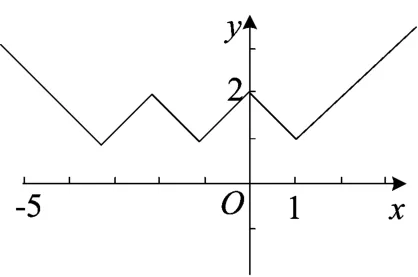
图2

如取k1＝1,k2＝－1,k3＝1,k4＝－1,k5＝1,则折线段的斜率从左至右依次－1、1、－1、1、－1、1,可得到锯齿形的函数(如图2)y＝x＋3－x＋2＋ x＋1－x＋x－1;

如取k1＝1、k2＝1、k3＝1、k4＝1、k5＝1,则折线段的斜率从左至右依次－5、－3、－1、1、3、5,可得到类“V”形的函数(如图3)y＝x＋3＋x＋2＋x＋1＋x＋x－1.

为说明以上性质的应用,举如下几个例题:

例1 (2011年“北约”自主招生)

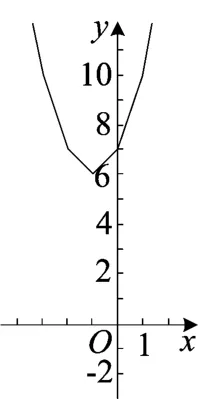
图3

求f(x)＝x－1＋2x－1＋…＋2011x－1的最小值.

则绝对值的系数均为正,由推论4知折线率从左至右由负到正,单调增大,设上线段斜率绝对值最小,即

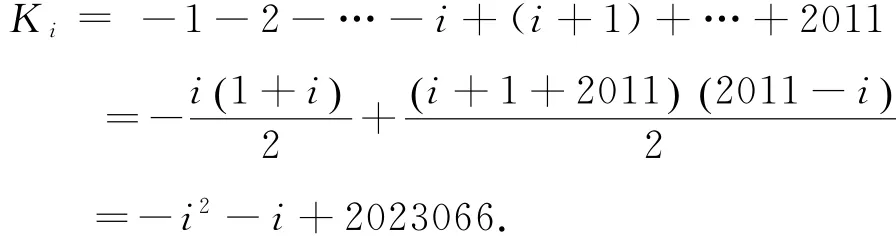
有最小绝对值,可令－i2－i＋2023066＝0,解得i≈1421.85,当i＝1421时,Ki＝2404;当 i＝1422时,Ki＝－440;故当i＝1422时,区间上线段有最小斜率绝对值,且斜率为负,所以时,函数有最小值

例2 讨论函数y＝x＋1＋ax ＋x－1在a取何值时,只有最大值;在a取何值时,只有最小值;在a取何值时,既有最大值又有最小值.

解 根据推论3,当1＋a＋1＞0,即a＞－2时,函数有最小值;当1＋a＋1＜0,即a＜－2时,函数有最大值;当1＋a＋1＝0,即a＝－2时,函数有最小值也有最大值.

注 有兴趣的读者可以考虑在a取何值时,在x＝0处最小(大)值;a取何值时,在x＝1处最小(大)值.

例3 已知x＋y＋z＝3,求证:2x－1＋2y－1＋2z－1＋3x＋1＋3y＋1＋3z＋1≥18.

证明 构造函数f(x)＝2x－1＋3x＋1,由推论4,f(x)为凸函数,根据詹森不等式,

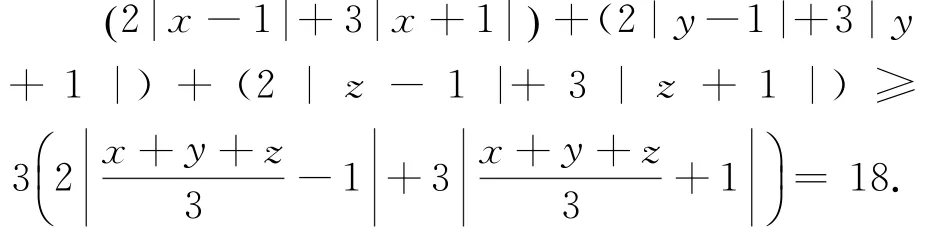
故所证不等式成立.

例4 讨论含参数k的方程－x＋3＋x＋2－x＋1＋x ＝kx－2解的情况.

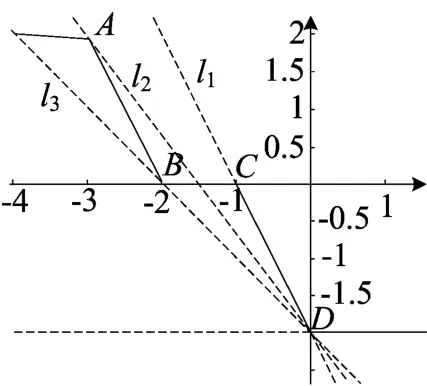
图4

解 方程可化为函数y＝－x＋3＋x＋2－x＋1＋ x与y＝kx－2图象的公共点问题.由基本性质易知函数y＝－|x＋3 |＋|x＋2|－|x＋1|＋|x|的五条折线段的斜率依次为0,－2,0,－2,0,四个折点A－3,2()、B－2,0()、C－1,0()、D0,－2(),函数y＝kx－2图象恒过0,－2(),(如图4)CD、AD、BD的斜率依次为,由图易得:当k∈(－∞,－2)∪(0,＋∞)时,两个图象有唯一公共点,方程有唯一解0;

当k＝0时,方程的解集[0,＋∞);

当k＝－2时,方程的解集[－1,0];

当k＝－1时,方程有3个解,－4、－2,0;当k∈(0,－1)时,方程有2个解,一解为0,一解在区间(－∞,－4)内.

2017-06-02)