错在哪里

数 学园 地

错在哪里

1 江苏省海州高级中学

佟成军 (邮编:222062)

题目 已知f(x)是定义在R上的周期为4的奇函数,且当x∈(0,2)时,f(x)＝ln(x2－x＋b).若f(x)在区间[－2,2]上有5个零点,则实数b的取值范围是_____.

错解 因为f(x)是定义在R上的周期为4的奇函数,所以f(0)＝0.

－f(2)＝f(－2)＝f(－2＋4)＝f(2),所以f(－2)＝f(2)＝0.

因为f(x)在区间[－2,2]上有5个零点,

所以f(x)＝ln(x2－x＋b)在x∈(0,2)上有1个零点,

即x2－x＋b＝1在x∈(0,2)上有1个实根,

即x2－x＋b－1＝0在x∈(0,2)上有1个实根.

设g(x)＝x2－x＋b－1,x∈(0,2),考虑到g(x)的对称轴为

解答错了!错在哪里?

错解中将“f(x)＝ln(x2－x＋b)在x∈(0,2)上有1个零点”转化为“x2－x＋b＝1在x∈(0,2)上有1个实根”,事实上,在时,x2－x＋b＜0,此时对x∈(0,2),f(x)＝ln(x2－x＋b)无意义,疏漏了函数的定义域,由此可知以上解法是错误的.究其原因,在于“存在x∈(0,2),使x2－x＋b＝1有1个实根”是一个存在性命题,与全称命题“对任意x∈(0,2),x2－x＋b＞0恒成立”不能相互替代,正确的解法需要两个命题同时满足.

正解 因为f(x)是定义在R上的周期为4的奇函数,所以f(0)＝0.

－f(2)＝f(－2)＝f(－2＋4)＝f(2),所以f(－2)＝f(2)＝0.因为f(x)在区间[－2,2]上有5个零点,所以f(x)＝ln(x2－x＋b)在x∈(0,2)上有1个零点,则

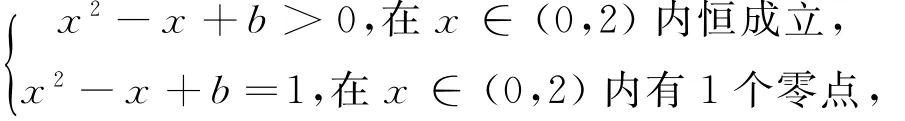
设g(x)＝x2－x＋b－1,x∈(0,2),考虑到g(x)的对称轴为

变式 已知关于x的方程lg(x＋a)＝2lg(x＋1)有且只有1解,则实数a的取值范围是____.

即方程x2＋x＋1－a＝0在x∈(－1,＋∞)上有1个实数解,

变式中的x＋a＞0在x＋1＞0且x＋a＝(x＋1)2时可以省略,在于这里是全称命题,与原题是有区别的.在转化问题时,要能够分清是存在性命题还是全称命题,从而保证问题的等价转化,预防可能产生的逻辑性错误.

2 江苏省常熟市中学

查正开 (邮编:215500)

问题 已知f(x)是定义在R上的函数,满足f(0)＝1,且对于任意的实数x、y都有f(xy)＝f(x)－y(3x－y＋1)成立,求f(x)的表达式.

解法1 在等式f(x－y)＝f(x)－y(3xy＋1)中令y＝x,得f(0)＝f(x)－x(3x－x＋1)＝f(x)－2x2－x.

再由条件f(0)＝1,得f(x)＝2x2＋x＋1.

解法2 在等式f(x－y)＝f(x)－y(3xy＋1)中令x＝0并结合条件f(0)＝1,得

f(－y)＝f(0)－y(－y＋1)＝f(0)＋y2－y＝y2－y＋1,

再取x＝－y,得f(x)＝x2＋x＋1.

解答错了!错误在哪里?

解法1与解法2的推理貌似都正确,但得出了不同的结果,说明两种解法中至少有一种是错误的,然哪种解法是正确的呢?哪种解法是错误的呢?

正解 在条件f(x－y)＝f(x)－y(3x－y＋1)中,将x视为常数并设x－y＝t,则y＝xt,于是

f(t)＝f(x)－(x－t)(3x－x＋t＋1)＝t2＋(x＋1)t－2x2－x＋f(x).

由此可知满足条件的f(x)必是二次函数形式.因此可设f(x)＝ax2＋bx＋c.

由f(0)＝1,得c＝1.则f(x－y)＝a(x－y)2＋b(x－y)＋1＝ax2＋bx－2axyay2－by＋1,

f(x)－y(3x－y＋1)＝ax2＋bx＋1－3xy＋y2－y,

要使任意的实数x、y都有f(x－y)＝f(x)－y(3x－y＋1)成立,当且仅当

所以满足条件的函数f(x)不存在,解法1与解法2都是错误的.

由于两种解法都是取特殊值得到的结果,它们只满足必要条件,并不能保证充分性.由解法1得到的函数f(x)＝2x2＋x＋1与解法2得到的函数f(x)＝x2＋x＋1都不能保证对于任意的实数x、y都有f(x－y)＝f(x)－y(3x－y＋1)恒成立.事实上,只要取x＝2,y＝1时以上两个函数都能使等式f(x－y)＝f(x)－y(3x－y＋1)不成立,所以结果均是错误的.故由此警示我们在利用特殊数值来解题时,一定要再验证所得结果的充分性(即检验),否则解题是不完整的甚至是要出错的.