创新思维在构造中升华——以三角函数问题为例

浙江省宁波市第四中学 蒋亚军 (邮编:315016)

浙江省宁波市李惠利中学 苏茂鸣 (邮编:315016)

创新思维在构造中升华
——以三角函数问题为例

浙江省宁波市第四中学 蒋亚军 (邮编:315016)

浙江省宁波市李惠利中学 苏茂鸣 (邮编:315016)

三角函数与代数、几何联系密切,题型丰富,变化万千,对某些用常规方法不易解决的三角问题,通过改变策略,依据题设的条件以及结构特点,挖掘问题的隐含条件,构造新的对应关系或新的数学模型,可以是代数构造,如函数、方程(组)、对偶式等;也可以是几何构造,如几何图形、几何意义等;呈现出问题的本质规律和数学的内在美,使复杂问题的求解变得简洁明了,给人耳目一新的感觉.

1 构“数”解题

从三角问题本身的特点出发构造辅助函数和方程(组),以沟通问题中条件与结论的联系,使问题中的隐含关系明朗化,从而简捷迅速地使问题获解.

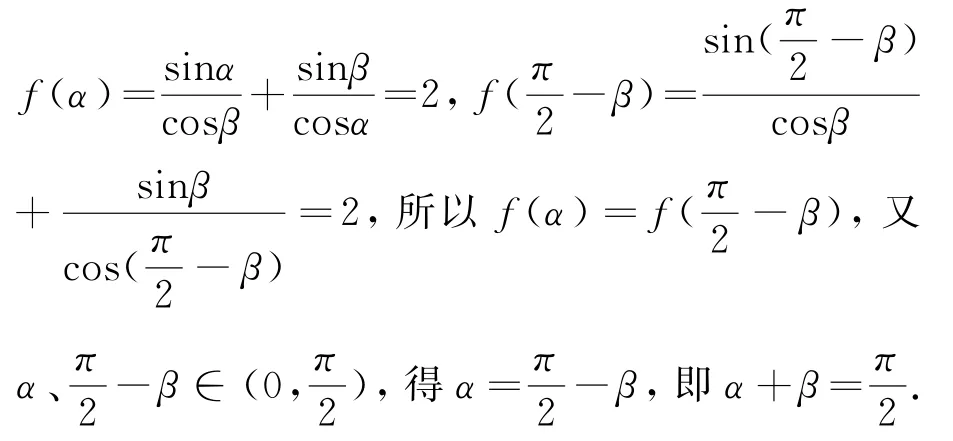
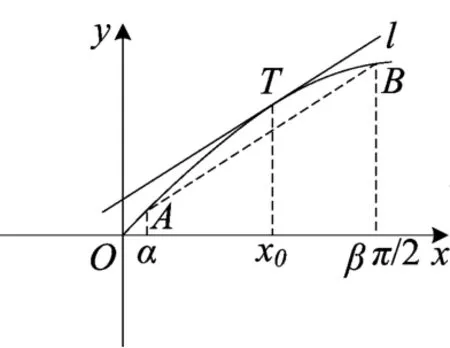
图1

证明2 本例几何意义如下:

因f(x)＝sinx,x∈(α,β)为增函数,0＜f′(x)＜1,f″(x)＜0,x∈(α,β),故,存在x0∈(α,β),使得y＝f(x)在 T(x0,f(x0))处的切线l平行于AB.即kAB＝即

评注 巧妙的构造函数,利用学生熟悉的函数性质来解决棘手问题,不仅训练了学生的思维,而且增强学生思维的灵活性和创造性,使解答别具一格,耐人寻味.例2的几何意义更是直观地将问题本质显现出来.

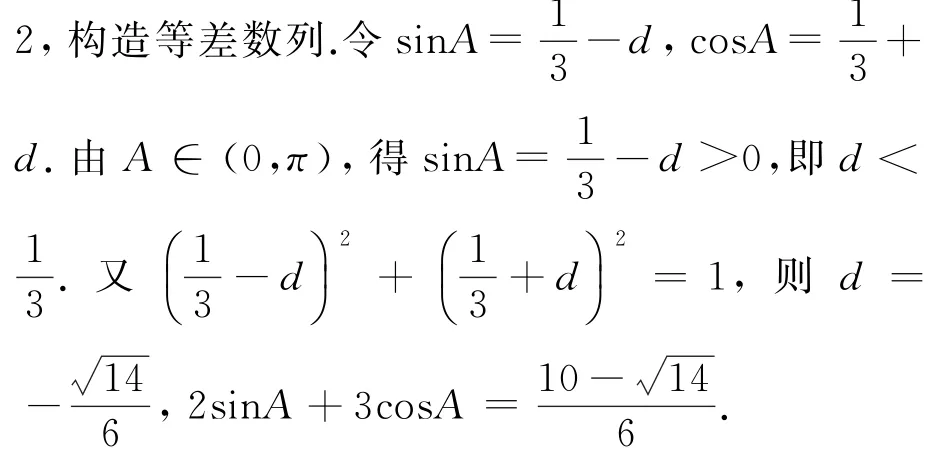
评注 解法1利用同角三角恒等式联立方程(组),思路自然,突出对三角公式的直接运用.解法2则是根据式子结构特点,构造等差数列,在知识交汇处有效地展示了创新思维,让学生体会构造是自然的,数学是清楚的、自然的.

2 造“形”破题

三角问题较为抽象,将题设中的数量关系以形象、直观的方式直接在图形中得到体现,利用几何性质(意义)使问题得到解决.

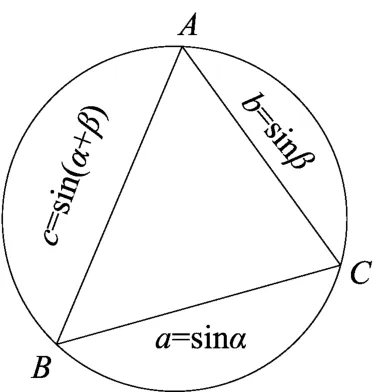
图2

例4 求sin223°＋sin237°＋sin23°sin37°的值.

解 如图2,取α＝23°, β＝37°,则a＝BC＝sin23°, b＝AC＝sin37°,c＝AB＝原问题转化为:在三角形ABC中,角 A、B、C的对边分别为a、b、c,已知A＝23°,B＝37°,求a2＋b2＋ab的值.因为cosC＝,所以

评注 基于三角形外接圆与正弦定理之间联系的构造,巧妙地将三角函数值转化为给定直径的圆的弦长,结合余弦定理使问题获解,避免了利用二倍角余弦公式降幂,积化和差以及和差化积公式带来的繁琐计算.

例5[2]函数f(x)＝(x∈[0,2π])的值域是( )(2008年重庆高考数学理科试题第10题)

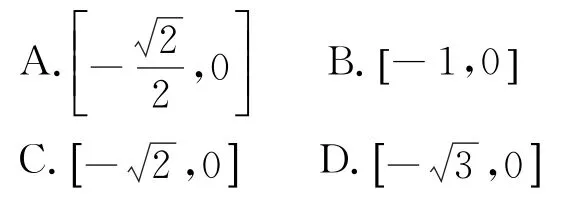
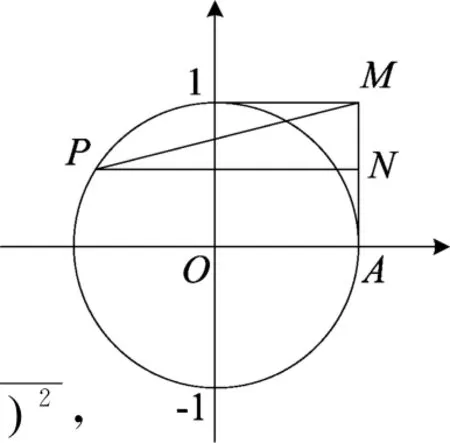
图3

评注 以上两种解法将问题巧妙地转化两个距离以及点到直线的距离,使得看似复杂的数学问题简单化,从而有效的减少计算量.

数学解题的过程就是把复杂的、生疏的、抽象的、困难的、未知的问题转化为简单的、熟悉的、具体的、容易的、已知的问题来解决[3].构造法恰能起到桥梁的作用,让隐含得以显露,使抽象变得直观,将三角函数与代数、几何有机地联系起来.在解题中要注重对学生思维深度的挖掘,透过问题的表象抓住本质,细致观察大胆构造,迅速制定解题策略,辩证地思考问题,加强学生数学基础知识的灵活运用,提高学生分析问题和解决问题的能力,拓宽学生的解题思路,从而培养学生的创新思维能力.

1 梁慧.三角函数变量代换解题方法探究[J].中学数学教学参考,2016(5):47-48

2 李红春.构造法巧解三角函数题[J].高中数学教与学, 2009(4):25-26

3 武松.运用划归求通项[J].高中数学教与学,2009(5): 14-16

2017-05-20)