由平面向量基本定理引出的几条等值线

浙江省绍兴鲁迅中学 虞关寿 (邮编:611731)

由平面向量基本定理引出的几条等值线

浙江省绍兴鲁迅中学 虞关寿 (邮编:611731)

平面向量基本定理是平面向量这一章最基本的内容之一.它是在学生掌握了向量的基本概念、向量的线性运算的基础上学习的,是向量坐标表示的逻辑前提,是用向量法求解几何问题的重要理论基础.从近几年的高考、竞赛试题明显感觉到对这个基本定理的考查力度,尤其对定理中内含于基底前的两个系数的深入考查.本文想通过两个系数的和、差、积、商的组合,结合近几年的高考、竞赛试题探究由这个基本引出的几条“等值线”,为各位考生备考之用.

1 系数之和为常数,即“λ＋μ＝k”引出等和线

①若λ＋μ＝1,则点A、P、B三点共线,此时的等和线是过A、P、B三点的一条直线,如图(1)中的直线l;

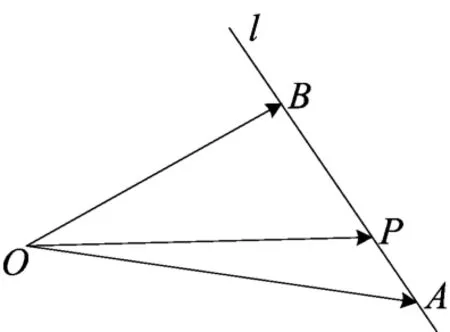
图(1)

②若λ＋μ＝k,且k∈(0,1),此时的等和线是与上面的直线l平行,且位于点O与直线l之间.如图(2)中的直线l1.容易得到

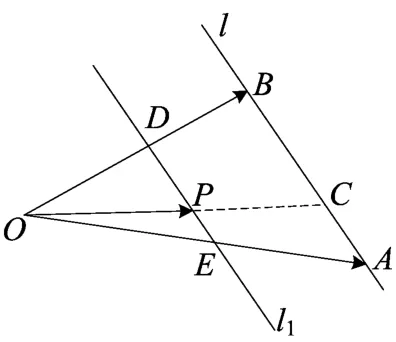
图(2)

③若λ＋μ＝k,且k＞1,此时的等和线是与上面的直线l平行,且直线l位于点O与直线l2之间.如图(3)中的直线l2.容易得到

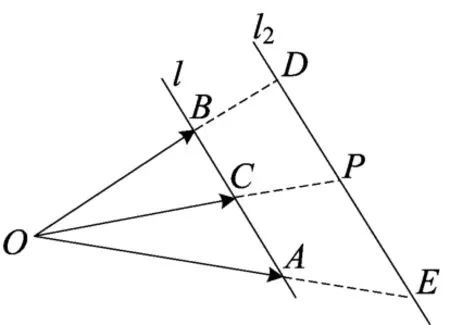
图(3)

④若λ＋μ＝k,且k＝0,此时的等和线是与上面的直线l平行,且过点O直线l0.如图(4)中的直线l0;

⑤若λ＋μ＝k,且k＜0,则所得的等和线与上面所得到的等和线关于O点对称.

图(4)

例1 (2016河北省高中数学竞赛)在△ABC中, D为边BC的中点,动点E在线段AD上移动时,若BE→＝λBA→＋μBC→,则s＝λ2

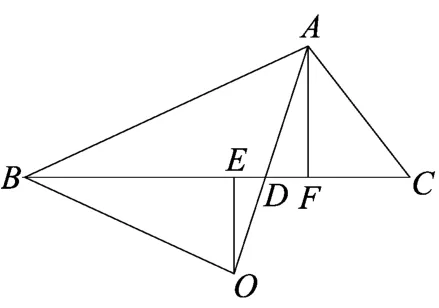
图(5)

解 如图(5),设AO交边BC于D点,过O作OE⊥BC,垂足为E,过A作AF⊥BC,垂足为F,易知设

例3(1) (2009安徽高考)给定两个长度为1的平面向量和,它们的夹角为1200,如图(6)所示,点C在以O为圆心的圆弧AB上变动.若,其中x、y∈R,则x＋ y的最大值是

所以λ∈[1,2],即(x＋y)max＝2.

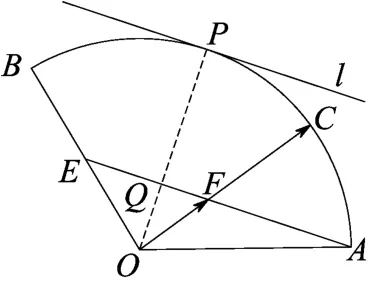
图(7)

(2)(2013杭州高考模拟)给定两个长度为1的平面向量和,它们的夹角为1200,如图(7)所示,点C在以O为圆心的圆弧AB上变动.若,其中x、y∈R,则x＋2y的取值范围是.

例4 (2017金华十校调研)设单位向量a、b夹角为θ,且θ为锐角,若对任意的实数对(x, y)∈{(x,y)||xa＋yb|＝1,xy≥0},都有|x成立,则a·b最小值为

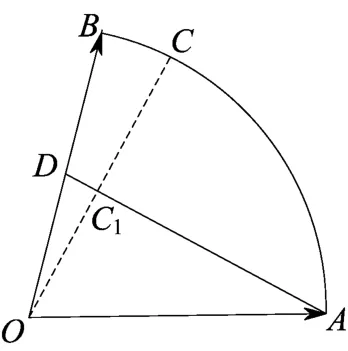
图(8)

当OC1⊥AD时,a·b取到最小值,因为a ·b＝|a||b|cosθ＝cosθ,此时利用余弦定理可得.所以a·b最小值为

2 系数之差为常数,即“λ－μ＝k”引出等差线

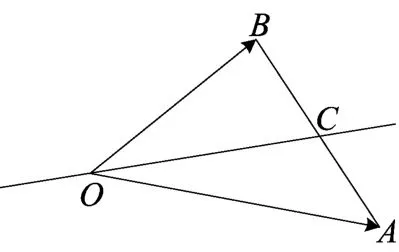
图(9)

①若λ－μ＝0,此时的等差线是过点O与线段AB中点C的一条直线,如图(9);

②若λ－μ＝1,此时的等差线是过点A与直线OC平行的一条直线,如图(10);

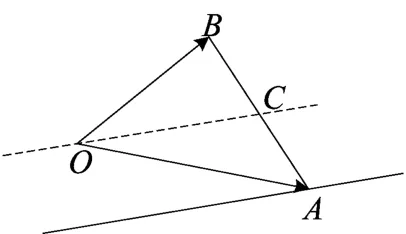
图(10)

③若λ－μ＝k,且k∈(0,1).此时的等差线是位于点A与直线OC之间,且平行OC的一条直线,如图(11),易求得k＝

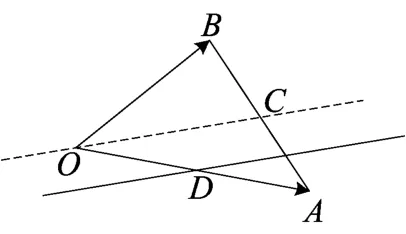
图(11)

④若λ－μ＝k,且k＞1.此时的等差线是位于BA延长上,且平行OC的一条直线,如图(12),易求得

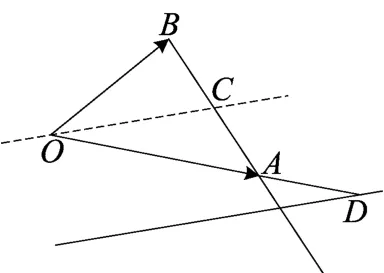
图(12)

⑤若两条等差线关于直线OC对称,则定值k互为相反数.

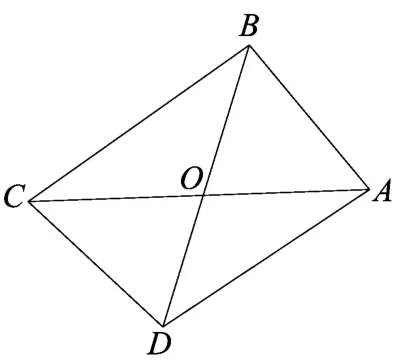
图(13)

例5 (2013安徽高考)在平面直角坐标系中, O是坐标原点,两定点A, B满足,则点集{P||λ|＋|μ|≤1,λ、μ∈R}所表示的区域面积是( )

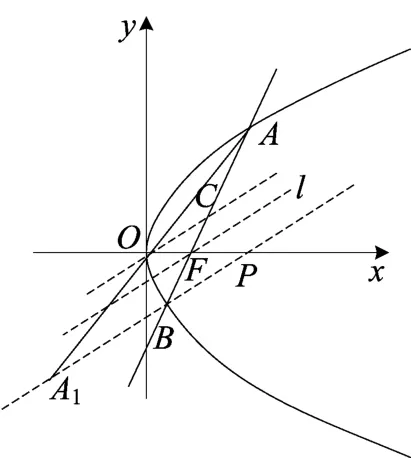
图(14)

解 如图(14),易知F(1,0),直线AB的倾斜角为600,弦AB的长为,由点差法可求得中点C的坐标为所以,因为即|,因为△FCO≅△FBP,所以|,由图知,直线AB为等和线,直线l为等差线,

3 系数之积为常数,即“λμ＝k(k≠0)”引出等积线

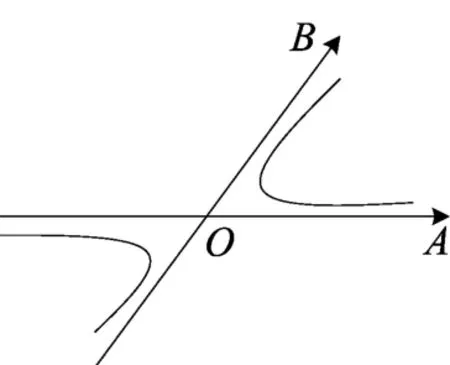
图(15)

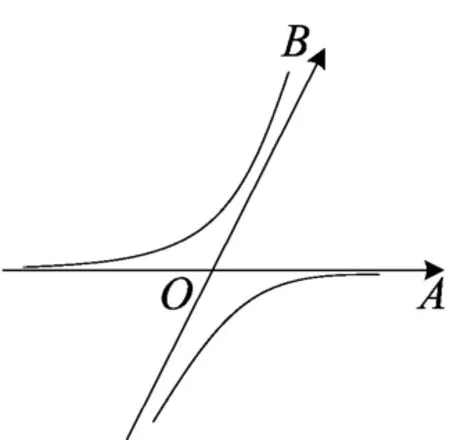
图(16)

例7(2010湖南省高中数学竞赛)已知直线x＝2与双曲线的渐近线交于E1, E2两点,记,任取双曲线Γ上的点P,若其中a,b∈R,则( )

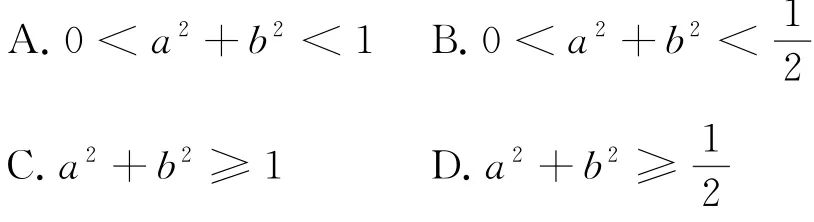
4 系数之商为常数,即”引出等商线

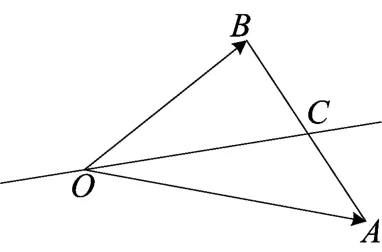
图(17)

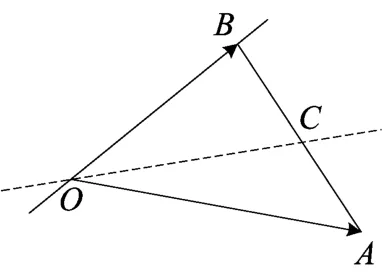
图(18)

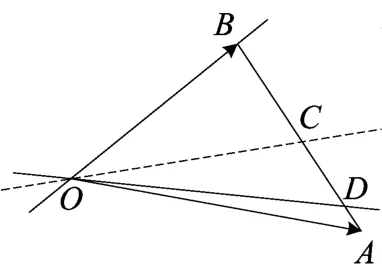
图(19)

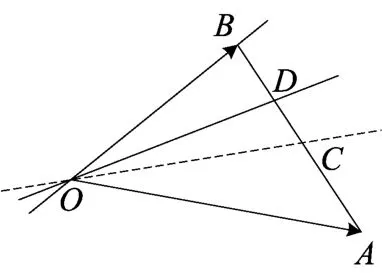
图(20)

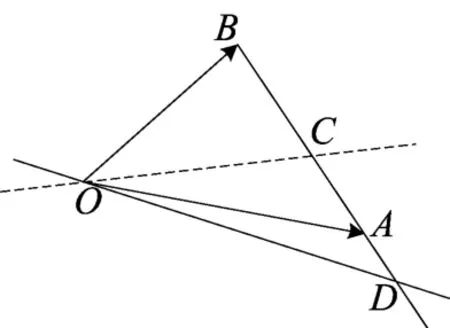
图(21)

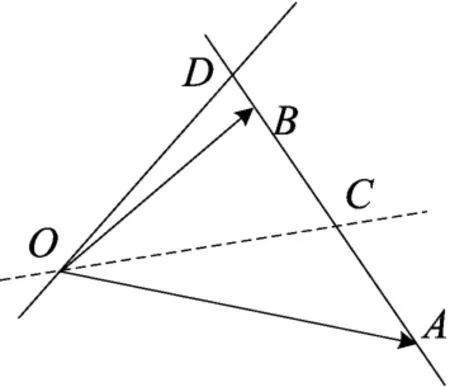
图(22)

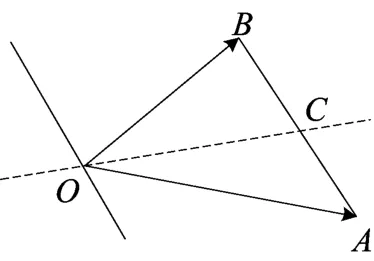
图(23)

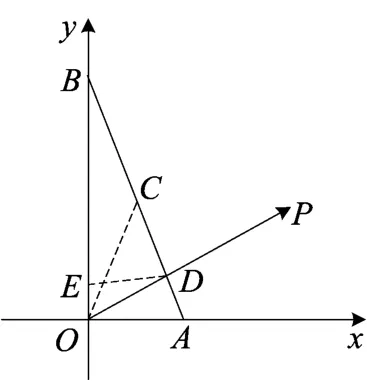
解 建立如图(24)的直角坐标系,由已知可得直线OP的方程为直线AB的方程为3x＋y－3＝0,联立可得点D的坐标为

图(24)

例10 (2012湖北省高中数学竞赛)在△ABC中,AB＝BC＝2,AC＝3.设O是△ABC的内心,若则的值为__________.

图(25)

2017-05-11)

本文为福建省教育科学＂十三五＂规划2016年度立项课题＂′核心素养′理念下的数学变式教学的行动研究＂(立项批准号MJYKT2016－178)的阶段性部分研究成果.