黄金分割图形荟萃 数学文化日渐风流——2017年安徽中考第23题赏析与研究

安徽省蚌埠市教育科学研究所 陈耀忠 (邮编:233000)

安徽省蚌埠市第六中学 仲立群 (邮编:233000)

黄金分割图形荟萃 数学文化日渐风流
——2017年安徽中考第23题赏析与研究

安徽省蚌埠市教育科学研究所 陈耀忠 (邮编:233000)

安徽省蚌埠市第六中学 仲立群 (邮编:233000)

2017年安徽初中学业水平考试数学试卷第23题作为压轴题,梯度明显、难度适宜、解法多样,源于教材基本图形,嫁接经典的黄金分割图形,立意高妙,蕴含丰富,启示一线教师从更深层次关注初中平面几何教学,思考初中数学教学.

解法研究;弦图、黄金分割;数学文化;教学启示

2017年中考落下帷幕,我们看到安徽省压轴题与前两年相比难度有所下降,风格也由前两年动态几何(双等腰三角形旋转变换)回归为确定性图形性质的研究,小题之间梯度明显,设问方式各不相同,问题难度层层递进,很好地落实课标精神、反映考纲要求,体现了学业水平考试的定位以及兼顾高中选拔的需求,是一道经典的平面几何好题.赏析如下:

图1

1 试题与解法研究

试题 (2017年安徽省初中学业水平考试数学试卷第23题)已知正方形ABCD,点M为边AB的中点.

(1)如图1,点G为线段CM上一点,且∠AGB＝90°,延长AG、BG分别与边BC、CD交于点E、F.

①求证:BE＝CF;

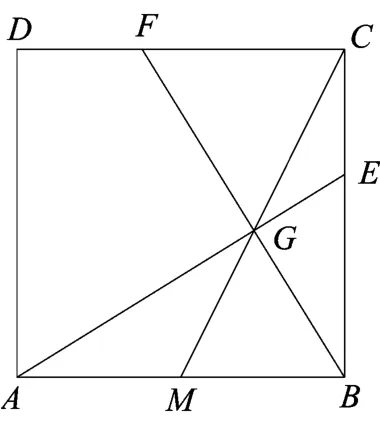
图2

②求证:BE2＝BC ·CE.

(2)如图2,在边BC上取一点E,满足BE2＝BC· CE,连接AE交CM于点G,连接BG并延长延长交CD于点F,求tan∠CBF的值.

本题以正方形为背景,因此解析法是比较容易想到的证法,限于篇幅,解析法和官方答案不再赘述!

下面重点研究第(1)小题第②问和第(2)小

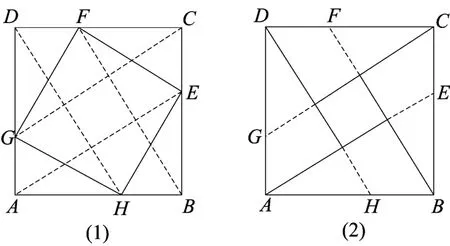
图15

定理2 点E、F、G、H分别在正方形ABCD的四条边BC、CD、DA、AB上(如图16),若EG⊥FH,则EG＝FH.

图16

图16 中E、F、G、H若为正方形四边中点,所得图形即为古埃及三角形(据传为古埃及构造3∶4∶5的直角三角形的图形,如图17),有以下性质:

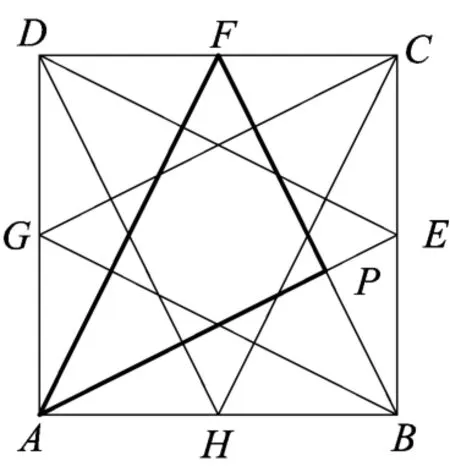
图17

定理3 已知E、F、G、H分别是正方形ABCD的边BC、CD、DA、AB的中点,AE、BF交于点P,则PF∶PA∶AF＝3∶4∶5.

本题证明不难,可以通过勾股定理计算得到,也可以通过建立直角坐标系运用解析法实现证明,还可以通过先证明PD＝PA,再延长DP交BE于点M进行证明(略).另外图18其实给出了一个无字证明(Without wordproof).

图18

由于图17具有对称性,内含极其丰富的性质,深受广大几何爱好者和命题专家的青睐,如下面例1.

图19

例1 (全国初中竞赛试题)在△ABC中,AB＝AC,AB⊥AC,D为AC中点,AE⊥BD交BC于E,交BD于H,求证:∠ADB＝∠CDE.

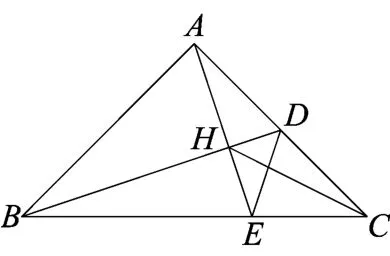
图20

本题证法多样,图形简洁,性质丰富.

本人结合自己的研究,根据此图曾在一些初中教师群中提出:

定理4 如图20,在△ABC中,AB＝AC,AB⊥AC.

①AD＝DC;②BE＝2EC;③AE⊥BD;④∠ADB＝∠CDE;⑤∠AEB＝∠CED;⑥∠BHC＝135°.

以其中任意两个作为条件均可证明其余四个结论都正确!

本图还有以下结论:

①∠DHC＝∠EHC;②∠ACH＝∠HBC;③∠BHC＝∠HAC;

④∠HBC＋∠HCB＝∠HAC＋∠HCA＝45°;

⑤△ABE∽△DCE;⑥△ACH∽△BHE;⑦BH∶HC＝

有兴趣的读者请自行研究,这也是初中平面几何练习很好的素材.

2 关于黄金分割点作图及图形性质研究

在本题中,其实给出了两种关于黄金分割点的作图:

方法一 (在直角边为1∶2的直角三角形中的作图)在直角△MBC中,MB∶BC＝1∶2,在MC上截取MG＝MB,则点G是线段MC的一个黄金分割点(如图1所示),即CG2＝CM ·GM.

方法二 (依托正方形作图,即本题第(1)问)在正方形ABCD中,取AB边的中点M,连接MC,并在MC上截取MG＝MB,延长AG交边BC于点E,则点E为线段BC的一个黄金分割点,即BE2＝BC·CE.

在几何原本中还有一种作法,介绍如下:

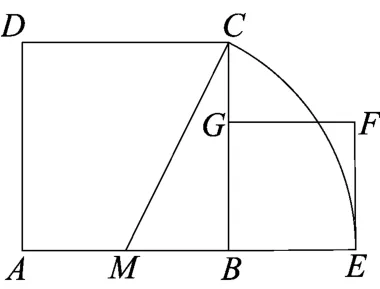
图21

方法三 在正方形ABCD中取边AB的中点M,以M为圆心,MC为半径做圆弧,交AB的延长线于E,以BE为边作正方形BEFG(如图21所示),点G在边BC上,则点G为线段BC的一个黄金分割点,即BG2＝BC·CG.

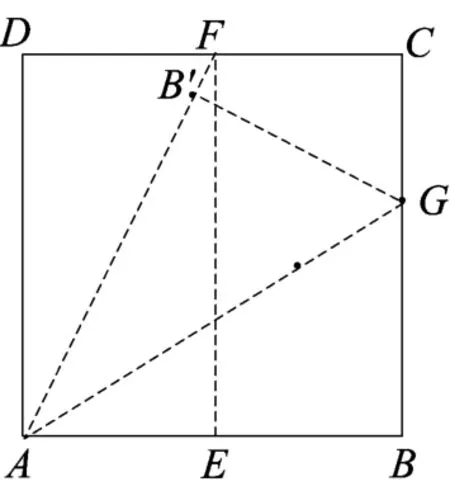
图22

其实,本题图形就源于方法三的作图,隐去辅助正方形,并以另一种方式呈现出来.上面的论述也证明了此作图的正确性.

图23

最近流行的折纸几何中也给出了另一种黄金分割点的给出方式:

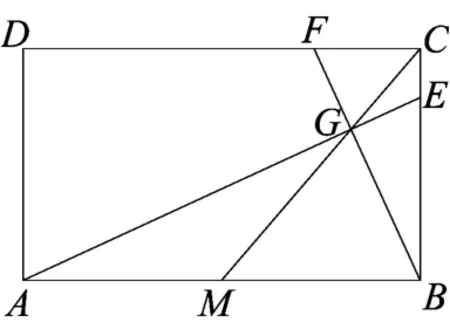
图24

方法四 将正方形ABCD对折,得到折痕EF,再次对折,得到折痕AF,铺平后折叠,使得点B落在折痕AF上(如图22),得到折痕AG(点G在BC上),则点G为线段BC的一个黄金分割点,即BG2＝BC·CG.(延长AF交BC延长线于M,利用AG平分∠FAB即可证明).

关于黄金分割点的产生有多种方式,如利用黄金矩形、黄金三角形等等都可以,在各种教材及各级考试中都有见到,在此不再整理,请各位同仁见谅!

3 问题延伸

从两个角度进行延伸:

3.1 正方形中BE∶EC与AM∶MB的数量关系研究

如图23,M为正方形ABCD的边AB上任意一点(与A、B不重合),以AB为直径的圆交CM于点G,AG、BG交BC、CD于E、F,若＝k,求的值.

延长AE、DC交于点N,不妨假设MB＝1,则AM＝k,AB＝BC＝k＋1,且设所求,则

当M为AB中点即k＝1时,是上述问题的特例.

3.2 将正方形一般化为矩形

如图24,M为长方形ABCD的边AB的中点,以AB为直径的圆交CM于点G,AG、BG交 BC、CD于E、F,则

证明比较简单,不再赘述!

4 教学启示

4.1 立足《课程课标》,重视挖掘教材,在教材中寻找教学素材和教学的衍生问题

教材是为了实现《课程标准》的要求编写的,为“学生的数学学习活动提供了学习主题、基本线索和知识结构”,是“实现数学课程目标、实施数学教学的重要资源”.

应该说,目前各版本的数学教材质量均是上乘的,内容清晰准确,素材丰富多样,过程符合教学需求,情景提供比较恰当,问题探究、例题示范、变式思考、练习反馈、课外延伸等栏目丰富.

教材中的例题、习题,以及公式、定理,其实都可以适度“变脸”或深度“改造”,甚至还可以进一步探究,其蕴含内容往往深刻而丰富.教学时,老师们要养成根据教学需要,不断从学生认知角度出发,挖掘服务于教学目标、有利于目标达成、立足于数学核心素养的教学素材,尤其是学生的反馈练习选择,不必完全照抄教辅资料上自认为很好的习题而忽视教材中的例习题.应该说,教材上的习题能很好地承接相关概念和典型例题,难度适宜,目的明确,寓意深刻,他们才是践行《课程标准》的真正意义上的好题.

近几年安徽都是以几何综合问题压轴,对广大考生和一线教师提出了挑战.但有趣的是,近几年压轴题都源于教材,高于教材,不仅给教学提供了丰富的教学素材,也指引我们一线教师如何跳出题海.在教材中多角度、多维度挖掘,立足基本图形的性质研究,揭示图形之间的内在联系,对经典数学名题深入思考,精心捕捉教材中的经典图形,对其衍生问题进行整合,抓核心素养,真正落实能力培养目标.

因此,读懂教材是教学设计的出发点,吃透教材是有效教学的支撑点,深入挖掘教材是保证教学的根本.日常教学不能舍本逐末,应该充分领会教材意图、深度研究整合教材素材,创造性地使用教材.

4.2 关注数学文化,传播数学之美,在经典中落实立德树人和核心素养目标

2014年4月,教育部印发《关于全面深化课程改革落实立德树人根本任务的意见》,如何体现国家关于立德树人的要求,不仅在教材编写上做出积极探索,也在各级命题中做出有益尝试.

近几年,安徽初中学业水平考试数学命题在这方面进行了有益的探索和尝试,如2016年第10题“布洛卡点”弱化在直角三角形中,第22题“阿基米德穷竭法”的再现,第23题“费马点”构图在问题解决中应用等.

今年安徽初中学业水平考试数学试题的命制延续了这种风格,本题就是一个典型代表,将“弦图”、“古埃及三角形”、“黄金分割”等融为一体.在数学史上,“黄金分割”与“勾股定理”被称为“几何双宝”,黄金分割这个数字一直被后人奉为科学和美学的金科玉律.本题的出现也为广大一线教师研究黄金分割提供了新的素材,也彰显了命题专家对数学文化的传承以及数学美学教育的关心.

无独有偶,今年安徽卷第16题选自中国古代《九章算术》的“盈不足”问题也备受瞩目,在弘扬中国传统文化做了有益尝试,也与全国高考命题思想达成一致.

为此,我们一线教师应在日常教学素材的选取上,挖掘教材时还应在数学发展的历史中寻求为人类文化发展做出重大贡献的数学名题,致敬经典,研究基本图,以此提高教学效果,提升教学品味,规避题海战术,将数学核心素养的培养落实在数学文化中,根植于历史命题中.

4.3 注重问题意识,着力问题联系,着力在几何教学中培养数学研究的基本过程

从近几年安徽初中学业水平考试数学试卷来看,试卷的第10题(选择题压轴题)、第14题(填空题压轴题)、第23题(解答题压轴题)基本都是以平面几何为命题点,可见命题老师对初中平面几何的教学现状有一定的思考.

实事求是的讲,作为逻辑推理能力培养的重要支柱——平面几何,在现在的中学数学教学改革中是被弱化的,从中考阅卷以及高中老师的反馈以及部分高校研究人员的研究中都对这种现象提出了质疑.如何在有限的平面几何教学内容和课时中保证数学教学目标,帮助初中学生能为进一步学习提供保障也就成为我们初中数学教师不可回避的课题,今年的安徽命题老师在这方面也做了积极回应:

从问题呈现上看,解答题第20题、第23题都是平面几何试题,问题的呈现极其严谨讲究:严格按照题目条件就可以做出相应几何图形,为研究试题提供保证,两道试题都与命题的逆命题有关:第20题回答了“一组对边相等、一组对角相等得四边形是不是平行四边形”,并给出一种可能的反例构图方式,事实上是从性质走向判定经常需要研究的话题;第23题(1)、(2)两问有着内在互逆的成分,联系2013年安徽第23题,反思教材关于数学研究对象的研究过程,都在不同程度展示了数学研究的基本过程:确定(认识)研究对象——研究对象性质——研究对象的判定(或运用性质解决问题),这些尝试或许透漏着命题老师对教学的思考、对数学研究的思考,更是对我们一线教师提出了一些希望!

总之,2017年安徽第23题是一道图形简洁、立意高妙、内涵丰富、梯度合适、难度贴切的一道经典试题.限于个人水平,挂一漏万,期待同仁批评指正!

2017-07-06)

本文系广东省教育科学“十三五”课题(课题批准号:2017YQJK134)《运用“问题串”开展高中数学教学的实践研究》的研究成果.