基于规则预计格网的开采沉陷等值线生成算法*
2021-01-07刘吉波王志红
刘吉波,王志红
(贵州工程应用技术学院 矿业工程学院,贵州 毕节 551700)
等值线图是一种非常重要的专题图型,常用的等值线图有等高线图、等深线图、等温线图、等压线图等。由离散点生成等值线,可采用Delaunay三角剖分算法根据离散点构建三角网,然后插值生成等值线,这种算法应用较广[1-5]。对于规则的格网状数据,由于其数据结构的特殊性,可不用建立三角网而直接生成等值线。这种方法直观,易编程实现,也有很多学者研究并实现[6-11]。本文结合开采沉陷数据处理特殊性,充分利用对角线上的数据,提高等值线精度,实现规则格网数据等值线的快速生成。
1 数据结构设计
设预计点有N行M列,分别位于网格点上,其位置由所在的行号和列号确定,如(i,j)。通过行列号的引用,每个矩形网格可自动分割成两个三角形,实际并未实施剖分,故称之为虚拟剖分,可大幅提高算法效率,如图1所示。
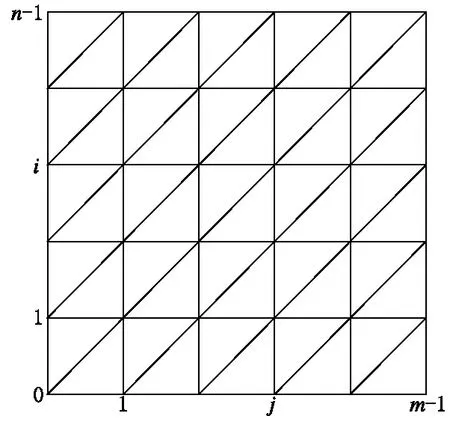
图1 规则网格点的虚拟三角剖分
设等值距为V,则可根据网格角点数据内插生成每条边(包括对角线)位于等值线上的点。当网格角点属性值恰好为等值距V的整数倍时,亦即网格点也是等值线上的点,将使等值线构造变复杂。为了降低算法复杂性,将该角点属性值加上一个不影响等值线生成精度的极小值ε,则可避免等值线过网格顶点时需多次进行路径判断问题,且不影响等值线精度。
对每个网格内的数据进行以下约定:对于网格(i,j),i、j为其左下角点的行号和列号,上部三角形编号为Ⅰ,下部三角形编号为Ⅱ,四条边及对角线的编号分别为①、②、③、④、⑤,每个网格编码方式相同,如图2所示。
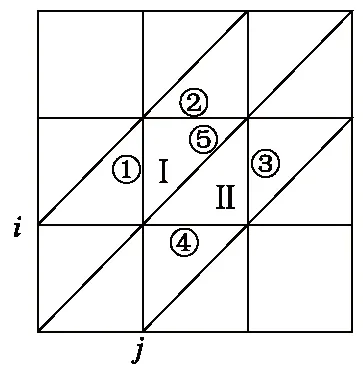
图2 网格(i,j)内三角形和边编号规则
2 等值线生成算法
2.1 起始三角形的确定
从编号为(0,0)的网格开始遍历,找到第一个需要绘制等值线的三角形所在网格。首先计算三角形三条边上当前等值线内插值的个数n,n可能为1,2或3。(Bb、Be)分别用来标记一个三角形内等值线段起点和终点所在的边的编号。当n=1时,Bb=Be=插值点所在的边的编号;当n=2时,第一段等值线的可能编号方式为(①,②)、(②,⑤)、(⑤,①)(对于△Ⅰ)或(③,④)、(④,⑤)、(⑤,③)(对于△Ⅱ),每个三角形有3种情形,若为逆时针,则将Bb和Be互换;当n=3时,则直接将这三个点连接构成闭合等值线。
2.2 下一个三角形的确定
如何寻找下一个要绘制的三角形是生成等值线算法的关键。当Be=①时,下一个要绘制的三角形位于网格(i,j-1),编号为Ⅱ;当Be=②时,下一个要绘制的三角形位于网格(i+1,j),编号为Ⅱ;当Be=③时,下一个要绘制的三角形位于网格(i,j+1),编号为Ⅰ;当Be=④时,下一个要绘制的三角形位于网格(i-1,j),编号为Ⅰ;当Be=⑤,位于△Ⅰ时,下一个要绘制的三角形位于网格(i,j),编号为Ⅱ;当Be=⑤,位于△Ⅱ时,下一个要绘制的三角形位于网格(i,j),编号为Ⅰ。
确定了下一个三角形位置后则可计算出新三角形中另一条等值线插值点所在的边,存储该点位置信息,并将其所在的边的编号赋值给Be。
重复上述过程,即可实现等值线的自动追踪,从而完成等值线绘制。
2.3 等值线追踪停止条件判断
一条等值线追踪停止或绘制完成的条件分以下2种情况:一种是当前等值线段的终点所在边的编号Be等于整条等值线的起点所在边的编号Bb,则停止追踪,此时等值线闭合,绘制完成,如图3中等值线A所示;另一种情况是当前等值线段的终点Be所在的边为网格数据的边界线时,停止追踪。对于后一种情况,多数情况下只是绘制了半条等值线。此时,需将已生成的等值线反向存储,并令Be=Bb,重复过程(2.2)和(2.3),生成等值线的剩余部分,从而完成整条等值线的绘制,此时等值线不闭合,如图3中等值线B所示。
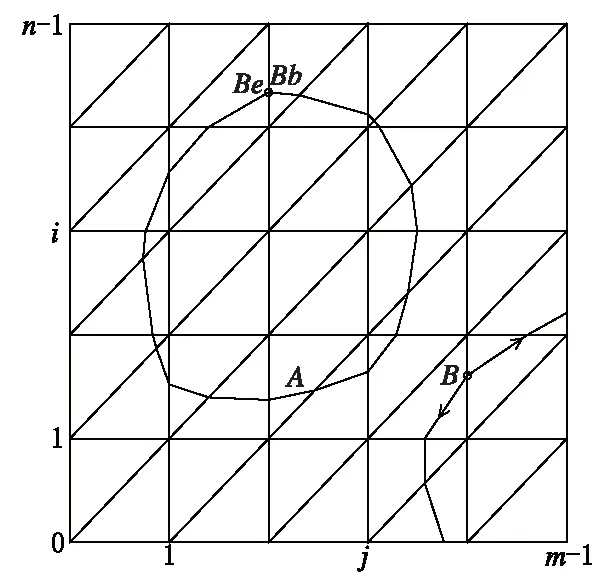
图3 等值线跟踪
当生成的等值线为逆时针存储时,需将等值线端点逆序重新存储,便于统一管理。
2.4 特殊等值线处理
在开采沉陷数据处理中,下沉边界等值线是由下沉值为10 mm的点构成,而不是下沉值为0 mm的点。同时,除下沉,倾斜、水平移动、曲率等变形都有正负之分(极少数情况下下沉也会出现),需要对正负零变形边界分别处理。
对于下沉边界,可以生成下沉值为10 mm的等值线,将其属性赋值为0 mm即可;而对于其他变形的正负0边界,可以用±ε(ε是个极小值)这两条特殊等值线代替,其属性值分别赋值为±0。
2.5 程序流程图
根据以上算法设计,由预计数据生成等值线的程序流程图如图4所示。
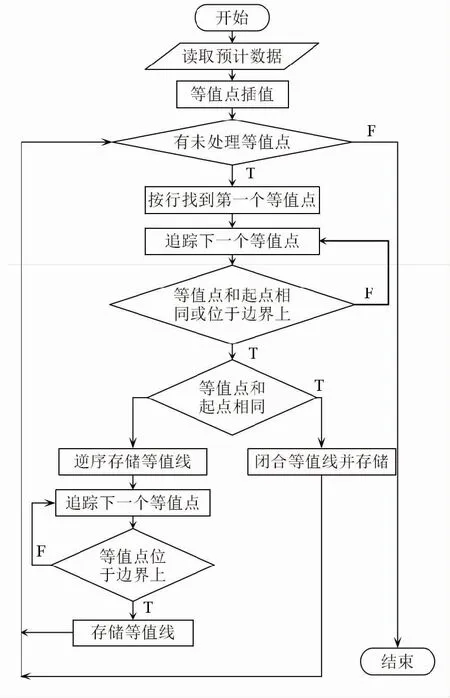
图4 程序流程图
3 等值线平滑
由于预计效率要求,预计网格点密度总是有限的,导致直接生成的等值线会呈现锯齿状,故需进行平滑处理。在要求不高的情况下,可采用质心平滑算法。即对于相邻三点构成的三角形,中间点的坐标用三角形质心坐标代替。采用平滑算法处理等值线简单且效果较好。
4 算法应用
在进行煤矿开采沉陷预计时,通常将预计点布设成网格状,根据预计网格点的变形值绘制相应的变形曲线。根据本文阐述的等值线生成算法,采用VC++ 6.0平台,即可实现规则网格数据等值线自动生成,等值线生成的函数代码如下,程序界面如图5所示。

图5 等值线绘制程序界面
void DrawContours(CFile ConFile)
{
int i,j,k,Flag,oneconSize;
double Value;
SP ConP;
CArray
CString Str1,ConLable,Formats;
GetBeginRowCol(0,0);
for(i=0;i for(j=0;j<2*(nx-1);j++) { GetBeginRowCol(beginrow,begincol); i=beginrow; j=begincol; if(j==2*(nx-1)) break; ConP=GetFirstP(i,j); Formats.Format("%%.%df
",3); ConLable.Format(Formats,ConP.v); Value=ConP.v; onecon.RemoveAll(); flagone=0; flagclose=0; if(DrawFirstTri(i,j,Value)) { Flag=DrawNextTri(i,j,Value); while(Flag) Flag=DrawNextTri(nr,nc,Value); if((IsEqual(onecon.GetAt(onecon.GetSize()-1).x,onecon.GetAt(0).x))&&(IsEqual(onecon.GetAt(onecon.GetSize()-1).y,onecon.GetAt(0).y))) flagclose=1; if((flagclose!=1)&&(flagone!=1)) { be=bb; temparray.RemoveAll(); for(k=onecon.GetSize()-1;k>=0;k--) temparray.Add(onecon.GetAt(k)); onecon.RemoveAll(); if(be==1) { GetPtAndSet0(grids[i][GridCol(j)].pny,grids[i][GridCol(j)].pointsy,Value,1,&ConP); SetGridFlag(i,j); if(j-1>=0) SetGridFlag(i,j-1); } if(be==2) { GetPtAndSet0(grids[i][GridCol(j)].pnx,grids[i][GridCol(j)].pointsx,Value,1,&ConP); SetGridFlag(i,j); if(i-1>=0) SetGridFlag(i-1,j-1); } if(be==3) { GetPtAndSet0(grids[i][GridCol(j)+1].pny,grids[i][GridCol(j)+1].pointsy,Value,1,&ConP); SetGridFlag(i,j); if(j+1<2*(nx-1)) SetGridFlag(i,j+1); } if(be==4) { GetPtAndSet0(grids[i+1][GridCol(j)].pnx,grids[i+1][GridCol(j)].pointsx,Value,1,&ConP); SetGridFlag(i,j); if(i+1 SetGridFlag(i+1,j+1); } if(be==5) { GetPtAndSet0(grids[i][GridCol(j)].pnxy,grids[i][GridCol(j)].pointsxy,Value,1,&ConP); SetGridFlag(i,j); if(Odd(j)) SetGridFlag(i,j-1); else SetGridFlag(i,j+1); } Flag=DrawNextTri(i,j,Value); while(Flag) Flag=DrawNextTri(nr,nc,Value); for(k=0;k temparray.Add(onecon.GetAt(k)); onecon.RemoveAll(); for(k=0;k onecon.Add(temparray.GetAt(k)); } if(flagclose==1) oneconSize=onecon.GetSize()-1; else oneconSize=onecon.GetSize(); if(oneconSize>=2) { ConFile.Write(ConLable,ConLable.GetLength()); if(flagclose==1) { for(k=0;k { Str1.Format("%.3f,%.3f
",onecon.GetAt(k).x,onecon.GetAt(k).y); ConFile.Write(Str1,Str1.GetLength()); } Str1="C
"; ConFile.Write(Str1,Str1.GetLength()); } else for(k=0;k { Str1.Format("%.3f,%.3f
",onecon.GetAt(k).x,onecon.GetAt(k).y); ConFile.Write(Str1,Str1.GetLength()); } } } else { if(onecon.GetSize()>=2){ ConFile.Write(ConLable,ConLable.GetLength()); for(k=0;k { Str1.Format("%.3f,%.3f
",onecon.GetAt(k).x,onecon.GetAt(k).y); ConFile.Write(Str1,Str1.GetLength()); } Str1="C
"; ConFile.Write(Str1,Str1.GetLength()); } } } } 以某煤矿开采沉陷预计为例,单一工作面开采,预计网格数为40×50个,可绘制下沉等值线如图6所示。 图6 某煤矿开采沉陷预计下沉等值线图 本文阐述了根据规则格网数据快速生成开采沉陷预计移动变形等值线的生成算法原理,并利用VC++ 6.0编程实现。研究表明,根据文中算法,程序编写较其他算法更为简单, 生成的等值线图效果较好,可用于其他规则形式数据处理。该算法主要处理对象为规则数据,具有专用性,适用范围受到限制。对于任意离散数据,可以由线性内插法生成规则数据后再应用本算法。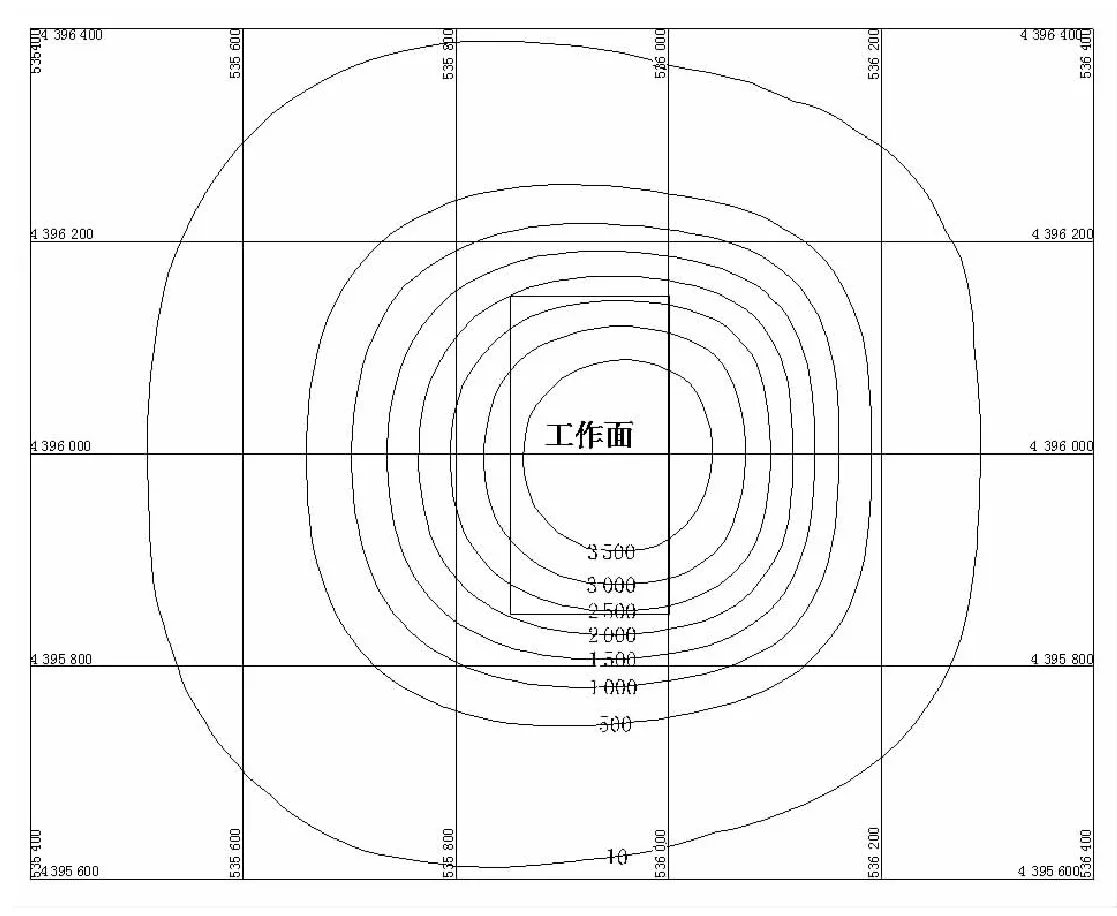
5 结 论
